Tangentialvektor
- derivative work: McSush (talk)
- Tangentialvektor.png: TN
Relevante Bilder
Relevante Artikel
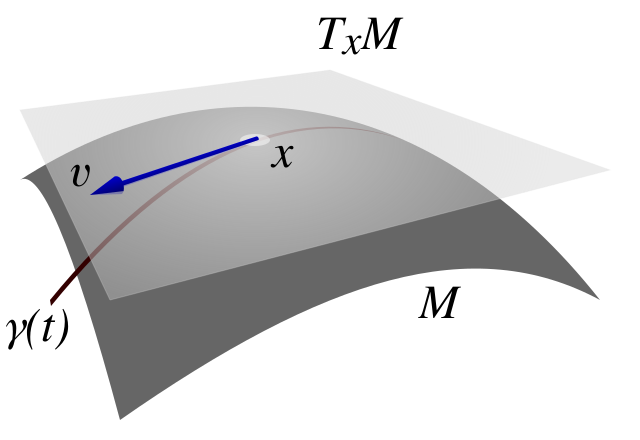
TangentialraumIn der Differentialgeometrie ist ein Tangentialraum ein Vektorraum, der eine differenzierbare Mannigfaltigkeit am Punkt linear approximiert. Sei eine differenzierbare Kurve mit und dem Kurvenparameter , dann ist: .. weiterlesen
TangentialebeneDie Tangentialebene in einem Punkt an eine Fläche im dreidimensionalen Raum ist diejenige Ebene, die die Fläche in der Umgebung des Punktes am besten annähert (berührt). Sie ist damit die zweidimensionale Entsprechung zur Tangente einer Kurve. Wie im Fall der Kurve existiert eine Tangentialebene nur, wenn die Fläche hinreichend „glatt“ ist. Dies gilt zum Beispiel für die Graphen von differenzierbaren Funktionen von zwei Variablen. Eine Fläche, die einen Knick oder eine Spitze hat – zum Beispiel ein Kegel – besitzt in diesen Punkten keine Tangentialebene. .. weiterlesen
Untermannigfaltigkeit des ℝnIn der Mathematik sind Untermannigfaltigkeiten des ein Begriff aus der Analysis und der Differentialgeometrie. Da die Untermannigfaltigkeiten Teilmengen eines euklidischen Raumes sind, erben sie von diesem viele Eigenschaften wie zum Beispiel die Möglichkeit Abstände zu messen. Jedoch kann man jede Untermannigfaltigkeit auch als abstrakte differenzierbare Mannigfaltigkeit betrachten. Die Äquivalenz der beiden Sichtweisen wird durch den Einbettungssatz von Whitney sichergestellt. .. weiterlesen