Zykloide von Ceva

Zykloide von Ceva

Die Zykloide von Ceva oder Trisektrix von Ceva ist eine nach Tommaso Ceva (1648–1736) benannte ebene Kurve, die zur Dreiteilung von Winkeln verwendet werden kann (daher Trisektrix). Ceva selbst bezeichnete die Kurve als cycloidum anomalarum.

Geometrische Definition

Animation der Konstruktion der Zykloide von Ceva

Winkeleigenschaft der Zykloide von Ceva:
${\displaystyle \varphi =\angle P_{1}OP_{2}=\angle P_{1}P_{2}O}$ (Basiswinkelsatz)
${\displaystyle 2\varphi =\angle P_{3}P_{1}P_{2}=\angle P_{3}P_{1}P_{2}}$ (Außenwinkelsatz, Basiswinkelsatz)
${\displaystyle 3\varphi =180^{\circ }-(180^{\circ }-4\varphi )-\varphi }$ (Nebenwinkel, Winkelsumme)

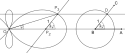
Für einen Punkt ${\displaystyle P_{1}}$ auf dem Einheitskreis konstruiert man die Verbindungsgerade ${\displaystyle OP_{1}}$ zum Ursprung ${\displaystyle O}$. Dann bestimmt man auf der x-Achse den von ${\displaystyle O}$ verschiedenen Punkt ${\displaystyle P_{2}}$, der von ${\displaystyle P_{1}}$ den Abstand 1 besitzt. Schließlich bestimmt man dann den von ${\displaystyle P_{1}}$ verschiedenen Punkt ${\displaystyle P_{3}}$ auf der Geraden ${\displaystyle OP_{1}}$, der von ${\displaystyle P_{2}}$ den Abstand 1 besitzt. Die Zykloide von Ceva ist nun die Ortskurve von ${\displaystyle P_{3}}$, die man erhält, wenn man den Punkt ${\displaystyle P_{1}}$ und damit auch die Gerade ${\displaystyle OP_{1}}$ um den Ursprung ${\displaystyle O}$ rotiert.

Die Ortskurve besteht aus vier am Ursprung anliegenden achsensymmetrischen Schlaufen, wobei die beiden an der x-Achse liegenden Schlaufen deutlich größer sind als die beiden an der y-Achse. Verwendet man statt der Geraden ${\displaystyle OP_{1}}$ lediglich einen Strahl ${\displaystyle OP_{1}}$, so entfallen die beiden kleinen Schlaufen an der y-Achse.

Aufgrund der Konstruktion beträgt der Winkel zwischen der Geraden ${\displaystyle OP_{1}}$ und der x-Achse genau ein Drittel des Winkels zwischen der Strecke ${\displaystyle P_{2}P_{3}}$ und der x-Achse (siehe Zeichnung), aufgrund dieser Eigenschaft lässt sich die Kurve als Trisektrix verwenden.

Setzt man das Konstruktionsverfahren für Punkte ${\displaystyle P_{1}}$, ${\displaystyle P_{2}}$ und ${\displaystyle P_{3}}$ für weitere Punkte ${\displaystyle P_{k}}$ fort, so erhält man für ungerade ${\displaystyle k}$ als Ortskurven der ${\displaystyle P_{k}}$ die Sektrizen von Ceva.

Gleichung und Parameterform

Aus der geometrischen Definition lässt sich mit Hilfe des Kosinussatzes die folgende Gleichung in Polarkoordinaten herleiten:

${\displaystyle r=1+2\cos(2\varphi )}$.

Als Parameterkurve ${\displaystyle \gamma :[0,2\pi ]\rightarrow \mathbb {R} ^{2}}$ in kartesischen Koordinaten erhält man die folgende Darstellung:

${\displaystyle \gamma (t)={\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}={\begin{pmatrix}2\cos(t)+\cos(3t)\\\sin(3t)\end{pmatrix}}}$.

Zudem ergibt sich die folgende Gleichung in kartesischen Koordinaten, womit die Zykloide von Ceva eine algebraische Kurve sechsten Grades ist:

${\displaystyle (x^{2}+y^{2})^{3}=(3x^{2}-y^{2})^{2}}$.

Winkeldreiteilung

Winkeltrisektion spitzer Winkel mit der Zykloide von Ceva

Winkeltrisektion stumpfer Winkel mit der Zykloide von Ceva

Die oben beschriebene Winkeleigenschaft der Zykloide von Ceva liefert die folgende Konstruktion zur Dreiteilung eines Winkels. Bei einem gegebenen Winkel ${\displaystyle \angle CBA}$ verlängert man zunächst den Schenkel ${\displaystyle AB}$ und zeichnet auf der Verlängerung die Zykloide mit ${\displaystyle AB}$ als x-Achse. Dann trägt man auf dem anderen Schenkel ${\displaystyle BC}$ die Strecke ${\displaystyle BD}$ mit der Länge 1 ab und zeichnet die Parallele zu ${\displaystyle AB}$ durch den Punkt ${\displaystyle D}$. Diese schneidet die Zykloide in dem Punkt ${\displaystyle P_{3}}$. Nun verbindet man den Punkt ${\displaystyle P_{3}}$ mit dem Mittelpunkt der Zykloide ${\displaystyle O}$ (Ursprung des Koordinatensystems), dann bildet die Strecke ${\displaystyle OP_{3}}$ mit der Verlängerung von ${\displaystyle AB}$ einen Winkel, dessen Winkelmaß genau ein Drittel des Winkelmaßes des Ausgangswinkels ${\displaystyle \angle CBA}$ beträgt. Man beachte hierbei, dass die Parallele im Falle spitzer oder stumpfer Winkel die Zykloide immer in zwei Punkten schneidet und damit zunächst zwei Punkte zur Bestimmung von ${\displaystyle P_{3}}$ zur Verfügung stehen. Handelt es um einen spitzen Winkel (${\displaystyle \angle CBA<90^{\circ }}$), so wählt man den näher am Winkel gelegenen Schnittpunkt als ${\displaystyle P_{3}}$. Im Falle eine stumpfen Winkels (${\displaystyle \angle CBA>90^{\circ }}$) hingegen wählt man den weiter entfernten Schnittpunkt als ${\displaystyle P_{3}}$.

Historisches

Tommaso Ceva (1648–1736), der Bruder von Giovanni Ceva (1647–1734), beschrieb die Kurve in seinem 1699 erschienenen Werk Opuscula mathematica und bezeichnete sie dort als cycloidum anomalarum. Die Winkeleigenschaft beziehungsweise die der Kurvenkonstruktion zugrunde liegende mathematische Idee geht auf Archimedes (287–212 v. Chr.) zurück, der sie benutzte, um eine Winkeldreiteilung mit Hilfe eines markierten Lineals durchzuführen.

Literatur

• Gino Loria: Spezielle algebraische und transscendente Ebene Kurven: Theorie und Geschichte. Teubner, 1902, S. 324–325
• Eugene V. Shikin: Handbook and Atlas of Curves. CRC Press, 1996, ISBN 9780849389634, S. 315
• Robert C. Yates: The Trisection Problem. National Mathematics Magazine, Band 15, Nr. 4 (Jan., 1941), S. 191–202 (JSTOR)
• Laszlo Nemeth: Sectrix Curves on the Sphere. KOG 19, Dezember 2015, S. 42–47
• Robert C. Yates: The Trisection Problem. Classics in Mathematics Education Series Volume 3, The National Teachers of Mathematics, Education Resources Information Center, 1971, S. 39–40 (Online-Kopie)
• Tommaso Ceva: Opuscula mathematica. Mailand, 1699, S. 31 (Online-Kopie)

Weblinks

Commons: Cycloid of Ceva – Sammlung von Bildern, Videos und Audiodateien

• Ceva Trisectrix and Sectrix auf mathcurve.com
• Trisection using Special Curves
• Eric W. Weisstein: Cycloid of Ceva. In: MathWorld (englisch).
• Die Winkeldreiteilung (Konstruktion mit zusätzlichen Hilfsmitteln)