Zykloide

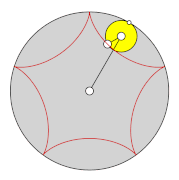
Eine Zykloide (v. lat. cyclus bzw. altgriechisch κύκλος kýklos = Kreis und ειδής -eidés = ähnlich), auch zyklische Kurve, Rad(lauf)- oder Rollkurve, ist die Bahn, die ein Punkt auf dem Umfang eines Kreises beschreibt, wenn dieser Kreis auf einer Leitkurve, zum Beispiel einer Geraden, abrollt. Eine Trochoide entsteht, wenn auch die Leitkurve ein Kreis ist (Rastkreis), wobei der betrachtete Punkt dabei außerhalb oder innerhalb des abrollenden Kreises (Gangkreis) liegt. Die Verwendung von Zykloiden und Trochoiden beim Zeichnen von Ornamenten fand durch das Spielzeug Spirograph weite Verbreitung.

Wer zuerst die Zykloide entdeckt bzw. näher untersucht hat, ist uns trotz ihrer einfachen Entstehungsweise – Betrachtung eines markierten Punktes auf einem bewegten Wagenrad – nicht überliefert. Nichts also hindert uns, anzunehmen, daß die Alten die Cykloide gekannt haben.^[1] Der anscheinend so einfache Verlauf der Linie lässt sich aber nicht allein mit Zirkel und Lineal konstruktiv darstellen.

Die erste Veröffentlichung zu Zykloiden erfolgte 1570 durch Gerolamo Cardano, der dabei unter anderem die cardanischen Kreise beschreibt.^[2] Galileo Galilei unternahm 1598 weitere geometrische Untersuchungen von Zykloiden.^[3]

Das 17. Jahrhundert, das als „Goldenes Zeitalter der Analysis“ gilt, war auch für die Untersuchung der Zykloide relevant. So beschäftigten sich die besten Mathematiker und Naturwissenschaftler mit dieser besonders ästhetischen Kurve.

Die erste Flächen- und Längenberechnung an einer Zykloide gelang 1629 dem Italiener Bonaventura Cavalieri.^[4] Weitere Forschungsanstöße lieferte im gleichen Jahr der Franzose Marin Mersenne.^[5]

Weitere Fortschritte durch Quadraturen schafften 1634 Gilles Personne de Roberval^[4] und 1635 René Descartes und Pierre de Fermat. Roberval gelang 1638 eine Tangentenkonstruktion,^[6] 1641 gelang dies auch Evangelista Torricelli. Torricelli entwickelte bis 1643 eine Quadratur in Beziehung zur Schraubenlinie. Der Engländer Christopher Wren zeigte 1658, dass die Länge einer Zykloide gleich dem Vierfachen des Durchmessers des generierenden Kreises ist.

Im Juni 1658 veröffentlichte Blaise Pascal unter dem Pseudonym Amos Dettonville einen Wettbewerb für die Lösung von sechs Problemen zur Zykloide: Bestimmung der von der Zykloide umschlossenen Fläche, Bestimmung des Schwerpunktes der umschlossenen Fläche, Berechnung der Volumina von Rotationskörpern um beide Achsen und Bestimmung der Schwerpunkte dieser Körper. Er wusste nicht, dass Roberval bereits in den 1630er Jahren die ersten vier Ergebnisse veröffentlicht hatte.^[7]

Eine Quadratur über eine unendliche Reihe erfolgte 1664 durch Isaac Newton.^[8] Gottfried Wilhelm Leibniz entwickelte 1673 die Quadratur über die Quadratrix.^[9] Der Niederländer Christiaan Huygens schaffte 1673 die Evolutenbestimmung^[10] und Tautochronie.

Leibniz stellte 1686 die Integraldarstellung fertig. Die letzte wichtige Erkenntnis war 1697 die Brachistochroneneigenschaft durch Johann I Bernoulli.^[11]

Eine Zykloide kann als analytische Gleichung und in Parameterdarstellung dargestellt werden. Die Parameterdarstellung lautet

${\displaystyle x=r(t-\sin(t));\quad y=r(1-\cos(t)),}$

wobei ${\displaystyle r}$ den Radius des Kreises und ${\displaystyle t}$ den Parameter („Wälzwinkel“) bezeichnet. Aus dieser lässt sich der Parameter ${\displaystyle t}$ eliminieren. Die analytische Gleichung lautet

${\displaystyle x(y)=r\arccos \left(1-{\frac {y}{r}}\right)-{\sqrt {y(2r-y)}},}$

beschreibt aber nur den Teil der Zykloide mit ${\displaystyle 0\leq x\leq r\pi }$.

Beliebige Zykloiden lassen sich durch folgende Parameterdarstellung berechnen:

${\displaystyle x=rt-c\sin(t);\quad y=r-c\cos(t),}$

wobei ${\displaystyle c}$ den Abstand des erzeugenden Punktes vom Mittelpunkt angibt. Zykloiden mit ${\displaystyle c<r}$ werden verkürzt, Zykloiden mit ${\displaystyle c>r}$ werden verlängert genannt. Diese beliebigen Zykloide lassen sich jedoch nicht mehr alle in einer analytischen Form darstellen.

Eine gewöhnliche Zykloide entsteht, wenn ein Kreis auf einer Geraden abrollt. Anschaulich gesprochen bewegt sich ein Punkt auf einem Reifen eines fahrenden Fahrrades (näherungsweise das Ventil) auf einer gewöhnlichen Zykloide. Die Katakaustik, die Evolute und die Evolvente der Zykloide sind selbst wieder Zykloiden. Die Mittelpunkte der Krümmungskreise einer Zykloide liegen vollständig auf ihrer Evolute.

Eine verkürzte Zykloide entsteht, wenn die Bahn eines Punktes im Inneren des Kreises betrachtet wird, anschaulich etwa der Seitenstrahler beim Fahrrad. Eine verlängerte Zykloide setzt dagegen voraus, dass ein Punkt außerhalb des abrollenden Kreises sich mit dem Kreis mitbewegt. Diese beiden Kurven heißen auch Trochoiden (altgriechisch τροχός trochos »Rad«).

Beispiele

• Gewöhnliche Zykloiden werden von Punkten auf der Lauffläche eines Autoreifens oder sonstiger Laufräder (Eisenbahn, Seilbahn) und von den Punkten längs der Lauffläche rollender Murmeln beschrieben.
• Verkürzte Zykloiden werden von Punkten mit einem Radius kleiner dem der Lauffläche beschrieben, etwa Punkte von Fahrradspeichen oder die Ansatzpunkte von Pleuelstangen bei einer Dampflokomotive.
• Verlängerte Zykloiden werden von Punkten mit einem Radius größer dem der Lauffläche beschrieben; im Fall von Eisenbahnen wären das alle Punkte des Spurkranzes.

Die Form einer gewöhnlichen Zykloide gleicht einer Aneinanderreihung weiterer Bögen, die verlängerte Zykloide weist an den Spitzen zwischen den Bögen noch Schleifen auf, während bei den verkürzten Zykloiden die Spitzen abgerundet sind.

Eine Brachistochrone beziehungsweise Tautochrone entsteht durch Spiegelung einer Zykloide an der x-Achse.

Die Länge der gewöhnlichen Zykloide mit der Parameterdarstellung ${\displaystyle x(t)=r(t-\sin(t)),\quad y(t)=r(1-\cos(t))}$ im Intervall ${\displaystyle [a,b]}$ kann mit dem Integral ${\displaystyle \int \limits _{a}^{b}{\sqrt {{\dot {x}}(t)^{2}+{\dot {y}}(t)^{2}}}\,\mathrm {d} t}$ berechnet werden. Mit den Ableitungen ${\displaystyle {\dot {x}}(t)=r(1-\cos(t))}$ und ${\displaystyle {\dot {y}}(t)=r\sin(t)}$ ergibt sich

${\displaystyle L=\int \limits _{0}^{2\pi }{\sqrt {(r(1-\cos(t)))^{2}+(r\sin(t))^{2}}}\,\mathrm {d} t=8r}$

Vorausgesetzt, dass Luftwiderstand und Reibung zu vernachlässigen sind, gelangt ein frei beweglicher Massenpunkt von jedem Startpunkt auf einer umgedrehten Zykloide stets in derselben Zeit an den tiefsten Punkt.^[12] Diese Eigenschaft wird auch Tautochronie genannt (Linie gleicher Fallzeit; altgriechisch ταὐτόtauto „dasselbe“, χρόνοςchronos „Zeit“).

Im 17. Jahrhundert zeigte Christiaan Huygens, dass beim Zykloidenpendel – ein Fadenpendel, bei dem sich der Faden an einer (passenden) Zykloide abrollt – die Schwingungsdauer unabhängig von der Auslenkung ist.^[13][14]

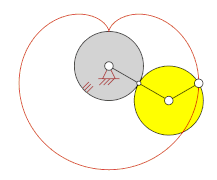
Rollt der Kreis außen auf einem anderen Kreis ab, entstehen Epizykloiden (altgriechisch ἐπίκυκλος epíkyklos, „Nebenkreis“). Ihr Radius ist gleich der Summe des Radius des Leitkreises und des Durchmessers des bewegten Kreises. Historisch versuchte man die beobachteten Planeten-Bahnen mit teilweise eigentümlich anmutenden Schleifen durch die Epizykeltheorie zu erklären. Rollt ein Kreis um einen feststehenden kleineren Kreis ab, entstehen Perizykloiden. Getriebetechnisch lässt sich das erzeugende Getriebe einer Perizykloide durch das Abrollen eines Hohlrades um ein stillstehendes kleineres Rad verwirklichen.

(c) I, NobbiP, CC BY-SA 3.0

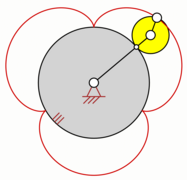
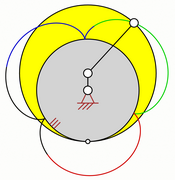
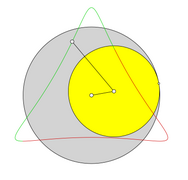
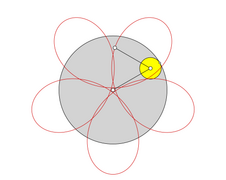
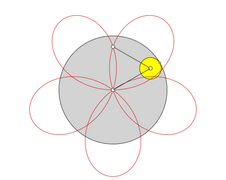
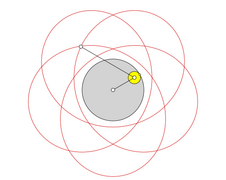
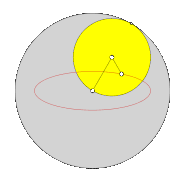
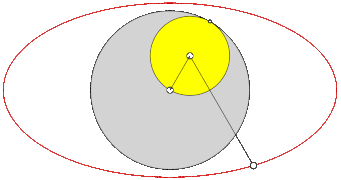
• Zweifache Erzeugung von Epizykloiden
• 
  Epizykloide q = 3/1
• 
  Perizykloide q = 3/4

(c) I, NobbiP, CC BY-SA 3.0

In der Mathematik werden beide Kurven häufig als Epizykloide bezeichnet, da sich die entstandene Kurve entweder durch das Abrollen eines Kreises auf einem anderen Kreis und auch durch das Abrollen eines Kreises um einen Kreis erzeugen lässt. Diese Erkenntnis wird zweifache Erzeugung von Zykloiden genannt.

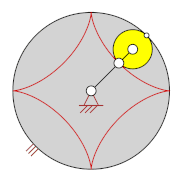
Rollt der Kreis dagegen innen in dem anderen Kreis ab, entstehen Hypozykloiden. Auch jede Hypozykloide kann analog zu Epizykloiden aufgrund der zweifachen Erzeugung von einem zweiten „Räderpaar“ erzeugt werden. Bei Hypozykloiden ist auch das zweite erzeugende „Räderpaar“ eine Hypozykloide: Bei einem der beiden „Räderpaare“ ist der Durchmesser des umlaufenden Innenrades kleiner gleich, bei dem anderen größer gleich dem Radius des feststehenden „Hohlrades“.

Sowohl Epizykloiden als auch Hypozykloiden sind genau dann geschlossene Kurven, wenn das Längenverhältnis ${\displaystyle q}$ = ${\displaystyle {\tfrac {R}{r}}}$ der Radien rational ist und sich durch Kürzen als gekürzter Bruch ${\displaystyle {\tfrac {i_{R}}{i_{r}}}}$ aus den zwei ganzen Zahlen ${\displaystyle i_{R}}$ und ${\displaystyle i_{r}}$ schreiben lässt. Mathematisch ausgedrückt bedeutet das: ${\displaystyle i_{R}={\tfrac {R}{\operatorname {ggT} (i_{R},i_{r})}}}$ und ${\displaystyle i_{r}={\tfrac {r}{\operatorname {ggT} (i_{R},i_{r})}}}$. Dabei bezeichnet ${\displaystyle \operatorname {ggT} (i_{R},i_{r})}$ den größten gemeinsamen Teiler von ${\displaystyle i_{R}}$ und ${\displaystyle i_{r}}$. ${\displaystyle R}$ ist in diesem Bruch der Radius der Rastpolbahn, also des rastenden und somit stehenden „Rades“, und ${\displaystyle r}$ ist der Radius der Gangpolbahn, nämlich des gehenden, also des umlaufenden „Rades“. Bei der technischen Umsetzung in Form von Zahnrädern ist die Anzahl der „Zähne“ maßgeblich, sodass sich stets geschlossene Kurven ergeben.

Die Anzahl der Spitzen der Epizykloiden während einer Periode ist identisch mit der ganzen Zahl ${\displaystyle i_{R}}$.

• Spezielle Hypo- und Epizykloiden
• 
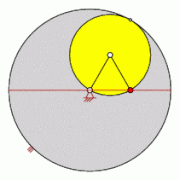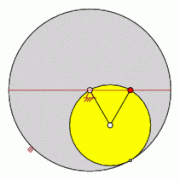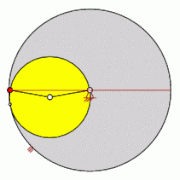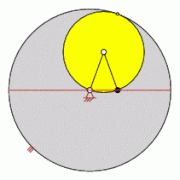
  Hypozykloide q = 2/1 (Cardanische Kreise)
• 
  Hypozykloide q = 3/1 (Deltoide)
• 
  Hypozykloide q = 4/1 (Astroide)
• 
  Epizykloide q = 1/1 (Herzkurve)

Für ganzzahlige Längenverhältnisse ${\displaystyle q}$ ergeben sich spezielle Epizykloiden oder Hypozykloiden:

• Für ${\displaystyle q=1}$ ergibt sich die sogenannte Herzkurve (Kardioide), eine Epizykloide.
• Für ${\displaystyle q=2}$ (Cardanische Kreise) ergibt sich eine geradlinige Hypozykloide, deren sämtliche Punkte auf einem Durchmesser liegen.
• Für ${\displaystyle q=3}$ ergibt sich eine Deltoide (Hypozykloide mit 3 Spitzen)
• Für ${\displaystyle q=4}$ ergibt sich eine Astroide: das Karo, wie man es von Spielkarten kennt.

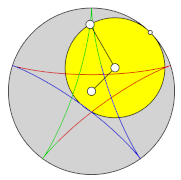
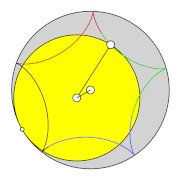
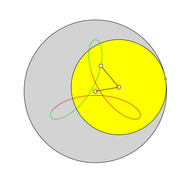
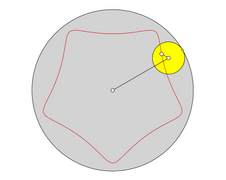
Die Anzahl an Umläufen des sich bewegenden „Rades“ während einer Periode ist ${\displaystyle i_{r}}$. In den Bildern wird für jeden Teil der Zykloide, der während eines Umlaufs des bewegten „Rades“ entsteht, eine andere Farbe verwendet.

• Anzahl Umläufe und Anzahl Schnittpunkte bei Zykloiden
• 
  Hypozykloide q = 5/1
• 
  Hypozykloide q = 5/3
• 
  Hypozykloide q = 5/2
• 
  Hypozykloide q = 5/4

Die Anzahl der Schnittpunkte s₀ von Epizykloiden ist gleich ${\displaystyle i_{R}\cdot (i_{r}-1)}$.^[15]

• Diese Gleichung gilt auch für Hypozykloiden mit ${\displaystyle q\geq 2}$, also wenn der Durchmesser des umlaufenden Kreises kleiner gleich dem Radius des feststehenden Kreises ist.

Für Perizykloiden und für Hypozykloiden mit ${\displaystyle p\leq 2}$ gilt ${\displaystyle s_{0}=i_{R}\cdot (i_{R}-i_{r}-1)}$.

Neben den gewöhnlichen, nämlich den gespitzten Zykloiden gibt es die verlängerten und somit verschlungenen sowie die verkürzten und somit gestreckten Epizykloiden, Perizykloiden und Hypozykloiden, die häufig auch Epitrochoiden, Peritrochoiden und Hypotrochoiden genannt werden.

• gestreckte, gespitzte und verschlungene Hypotrochoiden
• 
  gestreckte Hypotrochoide q = 3/1
• 
  gespitzte Hypozykloide q = 3/1
• 
  verschlungene Hypotrochoide q = 3/1
• 
  verschlungene Hypotrochoide q = 3/2
• 
  gespitzte Hypozykloide q = 3/2
• 
  gestreckte Hypotrochoide q = 3/2

Alle gestreckten Epitrochoiden, Peritrochoiden und Hypotrochoiden weisen die gleiche Anzahl an Schnittpunkten auf wie die gespitzten, also ${\displaystyle s_{0}}$.

Die gestreckten Trochoiden lassen sich unterscheiden in Trochoiden mit Wendepunkten und ohne.

Der Krümmungsmittelpunkt von Trochoiden mit Wendepunkten wechselt in jedem Wendepunkt von einer Seite der Kurve auf die andere. Somit weisen diese Trochoiden Links- und Rechtskurven auf. Die Anzahl der Links- wie auch der Rechtskurven ist ${\displaystyle i_{R}}$ und damit gleich der Anzahl der Spitzen. Die Anzahl der Wendepunkte ist somit ${\displaystyle 2\cdot i_{R}}$. Punkte, die gestreckte Trochoiden mit Wendepunkten erzeugen, liegen in der Nähe des Randes des umlaufenden „Rades“.

Punkte, die gestreckte Trochoiden ohne Wendepunkte erzeugen, liegen weiter entfernt vom Rand des umlaufenden „Rades“.

Getrennt werden beide Bereiche durch den Sonderfall, dass die gestreckten Trochoiden eine genäherte Gerade durchlaufen. Dies ist der Fall, wenn der erzeugende Punkt auf der Ballschen Kurve liegt und somit folgenden Abstand ${\displaystyle d_{r}}$ zum Mittelpunkt des umlaufenden Rades aufweist: ${\displaystyle d_{r}=r_{r}/(1+i_{R}/i_{r})}$. Die Anzahl der genäherten Geraden ist gleich ${\displaystyle i_{R}}$ und damit gleich der Anzahl an Spitzen.

• gespitzte und gestreckte Hypotrochoiden
• 
  gespitzte Hypozykloide
• 
  gestreckte Hypotrochoide mit Wendepunkten
• 
  Gestreckte Hypotrochoide mit genäherten Geraden
• 
  gestreckte Hypotrochoide ohne Wendepunkte

Die Anzahl an Schleifen während einer Periode ist identisch mit der Zahl ${\displaystyle i_{R}}$ und somit identisch mit der Anzahl an Spitzen der Zykloide.

Verschlungene Trochoiden weisen mindestens ${\displaystyle i_{R}}$ Schnittpunkte mehr als die (gespitzte) Zykloide auf. Die genaue Anzahl an Schnittpunkten lässt sich nur ermitteln mit Hilfe von Übergangskurvenpunkten. Ein Übergangskurvenpunkt erzeugt eine Trochoide mit Berührungspunkten. Die Anzahl an Übergangskurvenpunkten und somit an Trochoiden mit Berührungspunkten ist gleich dem Integerwert von ${\displaystyle {\tfrac {i_{R}}{2}}}$. Somit treten keine Berührungspunkte auf, wenn ${\displaystyle i_{R}}$ gleich 1 ist.

Übergangskurvenpunkte lassen sich nicht analytisch berechnen. Die Ermittlung mit Hilfe von Näherungsverfahren ist nicht kompliziert, würde aber den Rahmen dieses Artikels sprengen. Daher sollen hier nur die Phänomene zur Erzeugung der Formenvielfalt der verschlungenen Trochoiden erläutert werden. Die Formen und deren Vielfalt ist so faszinierend, dass diese Faszination von einem speziellen Spielzeug genutzt wird, nämlich dem Spirograph. Mit einem Spirograph können manuell verschiedene blumig anmutende verschlungene Hypotrochoiden mit Hilfe eines Zeichenstiftes erzeugt werden. Der Stift wird durch ein Loch eines in einem Hohlrad umlaufen Zahnrades gesteckt und so lange über ein Papier geführt, bis sich eine geschlossene Kurve ergibt.

Dass durch geringe Variation des Abstandes des Loches zum Mittelpunkt des umlaufenden „Rades“ immer wieder anders anmutende Hypotrochoiden entstehen, lässt sich anhand der Sonderfälle erläutern, bei denen Trochoiden mit Berührungspunkten entstehen.

• verschlungene Hypotrochoiden mit i=5/1
• 
  gespitzte Hypozykloide
• 
  Verschlungene Hypotrochoide mit 5 Schnittpunkten
• 
  Verschlungene Hypotrochoide mit 5 Berührungspunkten
• 
  Verschlungene Hypotrochoide mit 15 Schnittpunkten
• 
  Verschlungene Hypotrochoide mit 10fach-Schnittpunkt und 5 Schnittpunkten
• 
  Verschlungene Hypotrochoide mit 15 Schnittpunkten

Verschlungene Trochoiden mit der Mindestanzahl an Schnittpunkten werden durch Punkte erzeugt, die in der Nähe des Außenrandes des umlaufenden Rades liegen. Die Anzahl der Schnittpunkte ist gleich der Anzahl an Spitzen plus ${\displaystyle i_{R}}$.

Der Integerwert von ${\displaystyle {\tfrac {i_{R}}{2}}}$ ergibt die Anzahl ${\displaystyle n_{b}}$ an Trochoiden mit Berührungspunkten. Ist ${\displaystyle n_{b}}$ größer null, so wird irgendwann einmal eine verschlungene Trochoide mit Berührungspunkten erzeugt, wenn der erzeugende Punkt vom Kreisumfang weg verschoben wird. Die Trochoide mit Berührungspunkten selbst weist noch eine unveränderte Anzahl an Selbstschnittpunkten auf. Aber wenn der erzeugende Punkt noch weiter weg verschoben wird, entsteht eine Trochoide ohne Berührungspunkt, deren Anzahl an Schnittpunkten sich um ${\displaystyle 2\cdot i_{R}}$ erhöht hat. Erzeugt das zugrunde liegende „Räderpaar“ mehr als eine Trochoide mit Berührungspunkten, wiederholt sich das gleiche (mehrmals), wenn der erzeugende Punkt weiter vom Kreisumfang entfernt wird und dadurch wieder zu einer Stelle gelangt, in der eine Trochoide mit Berührungspunkten erzeugt wird.

• Alle Punkte, die Trochoiden mit Berührungspunkten erzeugen, liegen zwischen dem Außenrand des umlaufenden „Rades“ und einem konzentrischen Kreis durch den Mittelpunkt des stehenden Rades. Wird der erzeugende Punkt weiter weg vom Rand des umlaufenden Rades über den Mittelpunkt des stehenden Rades hinweg verschoben, ändert sich an der Anzahl der Schnittpunkte nichts mehr und es treten auch keine weiteren Sonderfälle auf.

Punkte, die vom Mittelpunkt des umlaufenden „Rades“ weiter entfernt sind als der Abstand der Mittelpunkte beider „Räder“, erzeugenden Trochoiden mit der maximalen Anzahl an Schnittpunkten ${\displaystyle n_{\text{max}}}$.

• Wenn ${\displaystyle i_{R}}$ eine gerade Zahl ist, ist die maximale Anzahl an Schnittpunkten ${\displaystyle n_{\text{max}}=n_{s0}+2\cdot n_{b}\cdot i_{R}}$
• In allen anderen Fällen, nämlich wenn ${\displaystyle i_{R}}$ eine ungerade Zahl ist, gilt: ${\displaystyle n_{\text{max}}=n_{s0}+(1+2\cdot n_{b})\cdot i_{R}}$

Eine Trochoide, die durch den Mittelpunkt des feststehenden „Rades“ verläuft und mehr als einen Schnittpunkt aufweist, stellt immer einen Sonderfall dar:

• Ist ${\displaystyle i_{R}}$ eine gerade Zahl, dann weist diese verschlungene Trochoide mindestens einen Berührungspunkt auf. Gibt es mehrere Berührungspunkte, so liegen Berührungs- und Selbstschnittpunkte übereinander
• Ist ${\displaystyle i_{R}}$ eine ungerade Zahl, dann liegen mehrere Schnittpunkte der verschlungenen Trochoide übereinander.

• Einen Spezialfall stellen (gespitzte) Hypozykloiden mit ${\displaystyle q=2}$ dar, bei denen also der Durchmesser des umlaufenden Rades gleich dem Radius des stehenden „Rades“ ist. Diese Zykloide ist eine zweifach durchlaufene Gerade und weist gleichzeitig 2 Spitzen und Berührungspunkte auf. Alle nicht gespitzten Trochoiden sind Ellipsen und das zweite erzeugende Getriebe ist eine Hypotrochoide mit gleichem Übersetzungsverhältnis.

• Hypotrochoide i=2/1
• 
  Hypotrochoide: Ellipse
• 
  Hypotrochoide: Gerade
• 
  Hypotrochoide: Ellipse

• Für ${\displaystyle q=2}$ einer Epitrochoide ergibt sich aus einem speziellen Punkt im Innern des rollenden Kreises die Hüllkurve im Gehäuse des Wankelmotors.

In der Getriebetechnik ist die Zykloidenverzahnung eine von mehreren Techniken zur Verzahnung von Zahnrädern und Zahnstangen. In Zykloidgetrieben folgt die Kontur der Kurvenscheiben äquidistant einer Zykloide.

• Guilloche

• Joachim Erven, Dietrich Schwägerl: Mathematik für Ingenieure. Walter De Gruyter, 4. Auflage, 2011, ISBN 978-3-486-70796-0, S. 211–215
• Volker Jäkel: Einteilung einer eben bewegten Ebene in Felder mit qualitativ gleichen Koppelpunktbahnen unter besonderer Berücksichtigung der Übergangskurve, VDI Verlag GmbH, Düsseldorf 2000, ISBN 3-18-332401-6, Kapitel 4

• Die Eigenschaften der Zykloide aus mathematischer, physikalischer und historischer Sicht (Memento vom 23. März 2008 im Internet Archive)
• Mathematische Erklärung zu Zykloiden
• Ausführliche Erklärungen und Herleitungen
• Animation von Epi-, Peri- und Hypozykloiden mit Hinweisen zur Anzahl der Spitzen, Selbstschnittpunkten, Selbstberührungspunkten, genäherten Geradführungen und Wendepunkten
• Herleitung der Formenvielfalt von Epitrochoiden einschließlich interaktiver Berechnung von Punkten auf Übergangskurven und BALLscher Kurve
• Herleitung der Formenvielfalt von Hypotrochoiden einschließlich interaktiver Berechnung von Punkten auf Übergangskurven und BALLscher Kurve
• Interaktives Applet zur Erzeugung von Hypozykloiden (automatisch)
• Interaktives Applet zur Erzeugung von Hypozykloiden (von Hand)
• Cyclobahn, eine U-Bahn mit Zykloiden-Trasse