Ziegenproblem

Ist es vorteilhaft für den Kandidaten, die Tür zu wechseln?
Das Ziegenproblem, Drei-Türen-Problem, Monty-Hall-Problem oder Monty-Hall-Dilemma ist eine Aufgabe aus der Wahrscheinlichkeitstheorie. Es wird oft als Beispiel herangezogen, um zu zeigen, dass die menschliche Intuition zu Trugschlüssen neigt, wenn es um das Schätzen von Wahrscheinlichkeiten geht.[1]
Die Aufgabe wurde zuerst von dem Biostatistiker Steve Selvin formuliert. Er stellte sie 1975 im American Statistician in einem Leserbrief vor. Die Beschreibung war lose an den Ablauf der amerikanischen Spielshow Let's make a deal angelehnt (in Deutschland von Sat.1 unter dem Titel Geh aufs Ganze! produziert). Im englischen Sprachraum wurde die Aufgabe nach Monty Hall, dem Moderator der Spielshow, benannt.
1990 veröffentlichte Marilyn vos Savant einen Leserbrief, der die Aufgabe erstmals mit Ziegen und Türen formulierte, in ihrer Kolumne „Ask Marilyn“ im Magazin Parade. Dieser Leserbrief wurde danach im deutschen Sprachraum als Ziegenproblem bekannt.
Neuformulierung des Problems
Die Aufgabenstellung von Marilyn vos Savant beruht auf einem Leserbrief, den sie von Craig F. Whitaker aus Columbia, Maryland, erhalten hatte:
„Nehmen Sie an, Sie wären in einer Spielshow und hätten die Wahl zwischen drei Türen. Hinter einer der Türen ist ein Auto, hinter den anderen sind Ziegen. Sie wählen eine Tür, sagen wir, Tür Nummer 1, und der Showmaster, der weiß, was hinter den Türen ist, öffnet eine andere Tür, sagen wir, Nummer 3, hinter der eine Ziege steht. Er fragt Sie nun: ‚Möchten Sie die Tür Nummer 2?‘ Ist es von Vorteil, die Wahl der Tür zu ändern?“[2]
Ihre Antwort lautete:
„Ja, Sie sollten wechseln. Die zuerst gewählte Tür hat die Gewinnchance von 1⁄3, aber die zweite Tür hat eine Gewinnchance von 2⁄3. Hier ist ein guter Weg, sich das Geschehen vorzustellen. Nehmen Sie an, es gäbe eine Million Türen und Sie wählen Tür Nummer 1. Dann öffnet der Moderator, der weiß, was hinter den Türen ist, und der eine Tür mit dem Preis stets vermeidet, alle Türen bis auf Tür Nummer 777777. Sie würden doch sofort zu dieser Tür wechseln, oder nicht?“[3]
Für die Lösung machte vos Savant implizit mehrere Annahmen.[4] Das von ihr gelöste Problem hat die folgende Form:
Nehmen Sie an, Sie wären in einer Spielshow und hätten die Wahl zwischen drei Türen. Hinter einer der Türen ist ein Auto, hinter den anderen sind Ziegen.[2] Das Auto und die Ziegen sind vor der Show zufällig auf die Türen verteilt worden. Sie haben keine Information über die Position des Autos. Der Moderator weiß, was sich hinter den Türen befindet. Die Spielregeln lauten:[5][6][7]
- Sie wählen zuerst eine Tür aus. Diese bleibt geschlossen.
- Der Moderator muss nun eine der beiden verbleibenden Türen öffnen. Hinter der von ihm geöffneten Tür muss sich eine Ziege befinden.
- Nachdem der Moderator eine Tür mit einer Ziege geöffnet hat, fragt er Sie, ob Sie bei Ihrer ersten Wahl bleiben oder zur letzten verbliebenen Tür wechseln möchten.
Sie wählen eine Tür, sagen wir, Tür Nummer 1, und der Moderator, der weiß, was hinter den Türen ist, öffnet eine andere Tür, sagen wir, Nummer 3, hinter der eine Ziege steht. Er fragt Sie nun: ‚Möchten Sie die Tür Nummer 2?‘ Ist es von Vorteil, die Wahl der Tür zu ändern?[2]
Die zusätzlichen Annahmen sind nötig, weil die Aufgabenstellung von vos Savant mehrdeutig ist. Mueser und Granberg bezeichnen das Problem mit diesen Zusatzannahmen als Monty-Hall-Standard-Problem.[5] Mögliche Spielverläufe bei anderen Annahmen werden im Abschnitt vom launischen Moderator beschrieben.
Einfache Lösungen

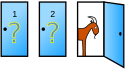
Das Auto steht hinter Tür 1, Tür 2 oder Tür 3. Die Abbildung zeigt den Spielverlauf für die drei Anfangszustände, wenn der Kandidat zuerst Tür 1 wählt.[8]
Wenn das Auto hinter Tür 3 steht, darf der Moderator gemäß Regel 2 weder Tür 1 noch Tür 3 öffnen. Er muss also Tür 2 öffnen. Der Kandidat gewinnt, wenn er zur noch geschlossenen Tür 3 wechselt.
Wenn das Auto hinter Tür 2 steht, muss der Moderator gemäß Regel 2 Tür 3 öffnen. Wieder gewinnt der Kandidat, wenn er zur noch geschlossenen Tür wechselt.
Nur wenn das Auto hinter Tür 1 steht, kann der Moderator wählen, ob er Tür 2 oder Tür 3 öffnet. Unabhängig von der Wahl des Moderators gewinnt der Kandidat das Auto, wenn er bei seiner ersten Wahl bleibt.[8]
Zusammenfassung: Der Kandidat wählt mit einer Wahrscheinlichkeit von 2⁄3 zuerst eine Tür, hinter der eine Ziege steht. In diesem Fall muss der Moderator die andere Tür mit einer Ziege dahinter öffnen. Dadurch gewinnt der Kandidat mit Wahrscheinlichkeit 2⁄3, wenn er wechselt. Nur wenn der Kandidat zuerst die Tür wählt, hinter der das Auto steht, gewinnt er, wenn er bei seiner ersten Wahl bleibt. Die Wahrscheinlichkeit dafür beträgt 1⁄3. Der Kandidat gewinnt mit einer Wahrscheinlichkeit von 2⁄3, wenn er wechselt, und mit einer Wahrscheinlichkeit von 1⁄3, wenn er bleibt.[6][9][10]
| Fall | Zuerst gewählt | Mit Wahrscheinlichkeit | Wechseln ist |
|---|---|---|---|
| 1 | Ziege | 2/3 | gut |
| 2 | Auto | 1/3 | schlecht |
Manche Quellen geben diese Lösung an, ohne den Einfluss von Regel 2 ausführlich zu erklären. Das kann dazu führen, dass man glaubt, dass man die einfache Lösung verstanden hat und danach versucht, sie auf Probleme zu übertragen, für die sie nicht zutrifft.[6]
Man kann auch die beiden nicht gewählten Türen gemeinsam betrachten. Wenn der Kandidat bei seiner ersten Wahl bleibt, bleibt seine Gewinnwahrscheinlichkeit bei 1/3. Wenn der Kandidat wechselt, dann wirkt sich das so aus, als ob er bei der ersten Wahl die beiden nicht gewählten Türen gewählt hätte. Dadurch steigt seine Gewinnwahrscheinlichkeit auf 2/3. Somit ist klar, dass er wechseln sollte.[7]
Formale Lösungen
Totale Gewinnwahrscheinlichkeit nach Türwechsel
Die Ereignisse zur Türwahl werden zerlegt in
- und : Der Kandidat hat anfangs die Tür zum Auto bzw. zu einer Ziege gewählt
- und : Der Kandidat hat nach dem Wechsel das Auto bzw. eine Ziege gewonnen.
Die anfängliche Wahl ist zufällig und mit den Wahrscheinlichkeiten und behaftet.
Wenn der Kandidat immer die Tür wechselt, ergeben sich durch Regel 2 der Problemformulierung die bedingten Wahrscheinlichkeiten und .[11]
Die gesuchte Wahrscheinlichkeit für den Autogewinn nach Wechsel der anfangs gewählten Tür ergibt sich mit dem Satz von der totalen Wahrscheinlichkeit als
- .
Der Wechsel verdoppelt die Gewinnchance von auf . Dieses Resultat ist unabhängig davon, ob der Moderator eine Tür bevorzugt öffnet, wenn er zwischen zwei Türen mit einer Ziege dahinter wählen kann.
Die relevanten Zahlenwerte und Formeln sind im Folgenden tabellarisch zusammengestellt.
Anfängliche Ereigniswahrscheinlichkeiten (ohne Türwechsel)
0 1 1 0
- : Bedingte Ereigniswahrscheinlichkeiten bei Türwechsel
0 1/3 2/3 0
- : Schnittwahrscheinlichkeiten der Ereignisse
- : Ereigniswahrscheinlichkeiten bei Türwechsel
Lösung des Einzelfalls mit dem Satz von Bayes
Es sind die Ereignisse definiert:
- : Der Gewinn ist hinter Tür ()
- : Der Moderator hat die Tür geöffnet ()
Es liegt folgende Situation vor: Der Kandidat hat Tür 1 gewählt, und der Moderator hat daraufhin Tür 3 geöffnet. Lohnt es sich für den Kandidaten zu wechseln? Wie groß ist die Wahrscheinlichkeit, dass das Auto hinter Tür 2 ist? Gesucht ist also die bedingte Wahrscheinlichkeit , dass das Auto hinter Tür 2 ist, wenn bekannt ist, dass es nicht hinter Tür 3 ist. Man kann diese Wahrscheinlichkeit mit dem Satz von Bayes ermitteln.
Dabei geht man von den bekannten Spielregeln und dem oben beschriebenen Einzelfall aus. Zusätzlich nimmt man an, dass der Moderator, wenn er zwischen zwei Türen mit einer Ziege dahinter wählen kann, jede der beiden Türen mit der gleichen Wahrscheinlichkeit 1⁄2 öffnet.[10] Damit ergeben sich folgende Wahrscheinlichkeiten:
Die Anwendung des Satzes von Bayes ergibt dann:
Der Kandidat sollte also wechseln, um seine Gewinnchancen von anfangs 1⁄3 auf nun 2⁄3 zu verdoppeln.
Kontroversen
Das Ziegenproblem wird oft kontrovers diskutiert.
Die meisten Menschen vermuten, dass es beim Monty-Hall-Standard-Problem keinen Unterschied macht, ob der Kandidat wechselt oder nicht. Viele begründen ihre Vermutung damit, dass es noch zwei geschlossene Türen gibt, hinter denen ein Auto und eine Ziege stehen, und deshalb die Gewinnwahrscheinlichkeit für beide Türen gleich hoch sei.[6] Diese Vermutung wird durch die einfachen Lösungen widerlegt.
Es gibt auch Diskussionen darüber, ob sich die Frage, ob der Kandidat wechseln sollte, konkret auf den beschriebenen Einzelfall bezieht oder ob dieser Einzelfall nur ein Beispiel für unterschiedliche Spielverläufe ist. Falls der Kandidat beim Monty-Hall-Standard-Problem zunächst Tür 1 mit einem Auto dahinter gewählt hat und der Moderator danach Tür 3 aufgrund einer Bevorzugung gegenüber Tür 2 geöffnet hat, dann unterscheidet sich für diesen Einzelfall die Gewinnwahrscheinlichkeit beim Wechseln von der totalen Gewinnwahrscheinlichkeit 2⁄3.[6] Ein solcher Einzelfall wird anhand des faulen Moderators ausgeführt.
Außerdem gibt es das Argument, dass die zusätzlichen Annahmen des Monty-Hall-Standard-Problems in der Aufgabenstellung von vos Savant fehlen. Bei anderen Annahmen wäre es beispielsweise auch möglich, dass der Moderator dem Kandidaten den Wechsel nur angeboten hat, weil dieser im ersten Schritt die Tür gewählt hat, hinter der das Auto steht und der Moderator ihn von dieser Tür weglocken möchte. Wenn der Kandidat zuerst eine Tür mit einer Ziege dahinter gewählt hätte, dann hätte der Moderator diese Tür sofort geöffnet und das Spiel beendet.[12] Dieses Argument wird anhand des launischen Moderators ausgeführt.
Varianten
Der faule Moderator
Bei dieser Variante des Monty-Hall-Standard-Problems bevorzugt der Moderator, wenn er wählen kann, eine bestimmte Tür, weil er möglichst wenig laufen möchte. Angenommen, er steht normalerweise neben Tür 3. Dann öffnet er immer die Tür mit der höchsten Zahl.
Die daran angepasste Regel 2 lautet: Der Moderator muss nun eine der beiden verbleibenden Türen öffnen. Hinter der von ihm geöffneten Tür muss sich eine Ziege befinden. Falls sich hinter beiden Türen eine Ziege befindet, öffnet er immer die Tür mit der höchsten Zahl.
Wenn also hinter der vom Kandidaten gewählten Tür 1 das Auto stünde, dann würde er mit Sicherheit Tür 3 öffnen und auf keinen Fall Tür 2.[6]
Einfache Lösung
Für die folgende Erklärung wird angenommen, dass der Kandidat zu Anfang Tür 1 gewählt hat.
Wenn der Moderator Tür 3 öffnet, muss das Auto hinter Tür 1 oder Tür 2 stehen. Die Wahrscheinlichkeit dafür, dass der Moderator Tür 3 öffnet, falls das Auto hinter Tür 1 steht, beträgt 1. Die Wahrscheinlichkeit dafür, dass der Moderator Tür 3 öffnet, falls das Auto hinter Tür 2 steht, beträgt ebenfalls 1. Also beträgt für diesen Einzelfall die Gewinnwahrscheinlichkeit für die beiden verbleibenden Türen jeweils 1⁄2.[6]
Wenn der Moderator hingegen Tür 2 öffnet, muss das Auto hinter Tür 3 stehen. Die Gewinnwahrscheinlichkeit für diesen Einzelfall ist 1, wenn der Kandidat wechselt, und 0, wenn er nicht wechselt.[6]
Formale Lösung
Es liegt die folgende Situation vor: Der Kandidat hat Tür 1 gewählt, und der Moderator hat daraufhin Tür 3 geöffnet. Für den oben beschriebenen Einzelfall gelten dann folgende Wahrscheinlichkeiten:
Die Anwendung des Satzes von Bayes ergibt dann für die bedingte Wahrscheinlichkeit, dass sich das Auto hinter Tür 2 befindet:
Für die bedingte Wahrscheinlichkeit, dass sich das Auto tatsächlich hinter Tür 1 befindet, gilt aber ebenfalls
Der Gewinn hinter Tür 2 ist genauso wahrscheinlich wie der Gewinn hinter Tür 1. Der Kandidat kann demnach in diesem Fall also ebenso gut bei Tür 1 bleiben wie zu Tür 2 wechseln. Hat der Moderator Tür 3 geöffnet, ist seine Gewinnchance also unabhängig vom Wechsel 1⁄2.
Der etwas faule Moderator
Bei dieser Variante des Monty-Hall-Standard-Problems lautet Regel 2: Der Moderator muss nun eine der beiden verbleibenden Türen öffnen. Hinter der von ihm geöffneten Tür muss sich eine Ziege befinden. Falls sich hinter beiden Türen eine Ziege befindet, öffnet er mit der Wahrscheinlichkeit die Tür mit der höchsten Zahl und die Tür mit der niedrigeren Zahl mit der Wahrscheinlichkeit .
Formale Lösung
Die Anwendung des Satzes von Bayes ergibt dann für die bedingte Wahrscheinlichkeit, dass sich das Auto hinter Tür 2 befindet:
Aus dieser Berechnung lassen sich der „neutrale Moderator“ () und der „faule Moderator“ () als Spezialfälle ableiten.[13]
Der unwissende Moderator
Der unwissende Moderator weiß nicht, hinter welcher Tür das Auto steht. Er entscheidet sich mit der gleichen Wahrscheinlichkeit für eine der beiden verbliebenen Türen. Er öffnet dabei gegebenenfalls auch die Tür mit dem Auto. Der Kandidat erhält keine neuen Informationen, wenn der Moderator eine Tür mit einer Ziege dahinter öffnet. Deshalb beträgt seine Gewinnwahrscheinlichkeit beim Wechseln 1⁄2. Das Gleiche gilt, wenn der Moderator sich mit der gleichen Wahrscheinlichkeit für eine der drei Türen entscheidet.[14][13][15]
Der launische Moderator
Der launische Moderator kann wählen, ob er einen Wechsel anbietet oder nicht. Die Gewinnchancen des Kandidaten hängen von seiner Laune ab.[12] Wenn er schlecht gelaunt ist, bietet er dem Kandidaten nur dann einen Wechsel an, wenn dieser im ersten Schritt die Tür gewählt hat, hinter der das Auto steht. Wenn hinter der Tür eine Ziege steht, öffnet er direkt diese Tür oder die Tür, hinter der ein Auto steht, und beendet damit das Spiel. Der Kandidat wählt im ersten Schritt mit Wahrscheinlichkeit 1⁄3 die Tür mit dem Auto dahinter. Wenn er nie wechselt, ist das seine Gewinnwahrscheinlichkeit. Wenn er immer wechselt, verliert er jeden Durchgang. Wenn der Moderator hingegen gut gelaunt ist, dann bietet er den Wechsel nur an, wenn der Kandidat im ersten Schritt eine Tür gewählt hat, hinter der eine Ziege steht. In diesem Fall gewinnt der Kandidat, wenn er immer wechselt und er verliert, wenn er nie wechselt. Der Kandidat kennt die Laune des Moderators nicht. Er kann sicherstellen, dass seine Gewinnwahrscheinlichkeit unabhängig von der Laune des Moderators genau 1⁄2 beträgt, indem er eine faire Münze wirft, um sich für oder gegen den Wechsel zu entscheiden.[16]
Das ältere Monty-Hall-Problem
Im Februar 1975 veröffentlichte die akademische Zeitschrift The American Statistician einen Brief von Steve Selvin, damals Assistenzprofessor für Biostatistik an der Universität von Kalifornien in Berkeley, an den Editor. In diesem Brief, überschrieben mit „A Problem in Probability“, schlug er eine Textaufgabe als Übung in Wahrscheinlichkeitsrechnung vor.[17] Die von ihm gegebene Lösung ähnelt der Tabelle, wie sie im Abschnitt zu vos Savants Antwort dargestellt ist. Im August desselben Jahres erschien ein weiterer Brief vom selben Autor mit dem Titel „On the Monty Hall Problem“, in dem er sich auf seinen ersten Brief bezog und auf Einwände seitens der Leser bezüglich seines Lösungsvorschlags reagierte. Zu diesem Zeitpunkt tauchte also zum ersten Mal der Begriff „Monty Hall Problem“ im medialen Raum auf.[18]
In seinem zweiten Brief präsentierte Selvin weitere Argumente zugunsten seiner Lösung, einschließlich einer formalen mathematischen Berechnung mithilfe bedingter Wahrscheinlichkeiten. Er fügte hinzu, dass seine Berechnungen auf bestimmten, nicht expliziten, Annahmen bzgl. des Verhaltens des Moderators Monty Hall beruhten. Außerdem zitierte er einen Leser, der darauf hinwies, dass die kritischen Annahmen bzgl. des Moderatorverhaltens notwendig seien, um das Problem überhaupt lösen zu können, und dass die Anfangsverteilung nur ein Teil des Problems darstellte, während es sich hier doch um ein subjektives Entscheidungsproblem handelte.
Es liegt nahe, dieses frühe Monty-Hall-Problem als einen Vorläufer der heute als Ziegenproblem bekannten Fragestellung anzusehen, einschließlich des Disputs über die damals schon umstrittenen zusätzlichen Annahmen bzgl. der Verhaltensregeln des Moderators.
Marilyn vos Savant und die Medien
Das Problem wurde auch außerhalb der Fachwelt bekannt, nachdem Marilyn vos Savant 1990 es in ihrer Kolumne „Ask Marilyn“ im Magazin Parade publiziert hatte. Ihre Version beruhte auf einem Leserbrief, den sie von Craig F. Whitaker aus Columbia, Maryland, erhalten hatte:[19]
„Nehmen Sie an, Sie wären in einer Spielshow und hätten die Wahl zwischen drei Türen. Hinter einer der Türen ist ein Auto, hinter den anderen sind Ziegen. Sie wählen eine Tür, sagen wir, Tür Nummer 1, und der Showmaster, der weiß, was hinter den Türen ist, öffnet eine andere Tür, sagen wir, Nummer 3, hinter der eine Ziege steht. Er fragt Sie nun: ‚Möchten Sie die Tür Nummer 2?‘ Ist es von Vorteil, die Wahl der Tür zu ändern?“[2]
Ihre Antwort lautete:
„Ja, Sie sollten wechseln. Die zuerst gewählte Tür hat die Gewinnchance von 1⁄3, aber die zweite Tür hat eine Gewinnchance von 2⁄3. Hier ist ein guter Weg, sich das Geschehen vorzustellen. Nehmen Sie an, es gäbe eine Million Türen und Sie wählen Tür Nummer 1. Dann öffnet der Moderator, der weiß, was hinter den Türen ist, und der eine Tür mit dem Preis stets vermeidet, alle Türen bis auf Tür Nummer 777777. Sie würden doch sofort zu dieser Tür wechseln, oder nicht?“[3]
Die Leserbriefe, die vos Savant danach erhielt, bezweifelten überwiegend die Richtigkeit ihrer Antwort. In späteren Folgen ihrer Kolumne veröffentlichte vos Savant weitere Erklärungen zu ihrer Lösung und den Inhalt einiger Leserbriefe, die ihrer Antwort teilweise heftig widersprachen.[3]
Dadurch wurde eine öffentliche Diskussion ausgelöst, von der auch die New York Times berichtete.[12] Die unterschiedlichen Positionen werden im Abschnitt Kontroversen erläutert.
Klärungsversuch der New York Times im Jahr 1991
In einem Artikel auf der ersten Seite der Sonntagsausgabe der New York Times[12] im Jahr 1991 wurde über den Versuch der Klärung der damals schon seit 10 Monaten währenden Debatte zur Lösung des „Monty-Hall-Problems“ berichtet. Zu diesem Klärungsversuch waren die folgenden vier Personen um ihren Beitrag gebeten worden: Martin Gardner, Persi Diaconis, Monty Hall und Marilyn vos Savant.
Nach einer Übersicht über den Verlauf der Diskussion bestätigt der erste Teil des Artikels, dass die Lösung von vos Savant unter ihren Zusatzannahmen korrekt ist. Persi Diaconis erklärte, es sei keine Schande, dieses Problem falsch zu beantworten. Unser Gehirn sei für Wahrscheinlichkeitsprobleme einfach nicht besonders gut geeignet. Martin Gardner nannte es „ein wunderbar verwirrendes kleines Problem“.
Der zweite Teil des Artikels beschreibt ein Beispiel dafür, dass die Formulierung der Aufgabenstellung auch andere Abläufe und damit auch andere Lösungen zulässt. Monty Hall las sich die Aufgabenstellung von vos Savant genau durch und spielte danach gegen einen Kandidaten. Dabei bot er dem Kandidaten nur dann einen Wechsel an, wenn dieser im ersten Schritt die Tür mit dem Auto dahinter gewählt hatte.
Gardner bestätigte diese Variante mit den Worten: „Das Problem ist nicht gut formuliert, wenn nicht klar gemacht wird, dass der Moderator immer eine Ziegentür öffnet und einen Wechsel anbietet.“ Sonst könnte der Moderator den Wechsel auch nur dann anbieten, wenn es zu seinem Vorteil wäre, den Kandidaten wechseln zu lassen, wodurch die Chancen bei einem Wechsel auf Null sinken würden. Diese Unklarheit könne beseitigt werden, indem der Moderator vorher verspreche, eine andere Tür zu öffnen und danach einen Wechsel anzubieten.
Vos Savant bestätigte diese Unklarheit in ihrer ursprünglichen Problemstellung und dass dieser Einwand, wenn er von ihren Kritikern gebracht worden wäre, gezeigt hätte, dass sie das Problem wirklich verstanden haben; aber sie hätten nie ihre erste falsche Auffassung aufgegeben. In ihrem später veröffentlichten Buch[4] schreibt sie, dass sie auch Briefe von Lesern erhalten habe, die auf diese Unklarheit hingewiesen hatten. Diese Briefe seien aber nicht veröffentlicht worden.
Diaconis sagte zur Aufgabenstellung: „Das strikte Argument lautet, dass die Frage nicht beantwortet werden kann, ohne die Motivation des Moderators zu kennen.“ Das stand ganz im Gegensatz zu den Veröffentlichungen, die ihre Lösung gerade auf exakte Mathematik im Gegensatz zur „Intuition“ gründeten.
Monty Hall selbst gab folgenden Rat: „Wenn der Moderator immer eine Tür öffnen und einen Wechsel anbieten muss, dann sollten Sie wechseln. Aber wenn er die Wahl hat, einen Wechsel anzubieten oder nicht, heißt es aufgepasst: Keine Gewähr! Alles hängt von seiner Laune ab.“
Paul Erdős und das Ziegenproblem
Andrew Vázsonyi[20] schildert, wie der berühmte Mathematiker Paul Erdős im Jahr 1995 auf das Ziegenproblem und die Behauptung der 2⁄3-Lösung reagiert hat. Nachdem Vázsonyi zunächst von einem Freund von dem Problem, direkt angelehnt an vos Savants Originalversion, gehört hatte, löste er es mit einem Entscheidungsbaum und konnte die 2⁄3-Lösung, die sich ergab, kaum glauben. Als er dann Problem und Lösung Erdős vorlegte, sagte „einer der größten Experten in Wahrscheinlichkeitstheorie“: Nein, das ist unmöglich. Da besteht kein Unterschied. Die Reaktion auf die Lösung mit dem Entscheidungsbaum beschreibt Vázsonyi so: Zu meiner Verblüffung überzeugte ihn das nicht. Er wollte eine einfache Lösung ohne Entscheidungsbäume. Ich gab an diesem Punkt auf, weil ich keine Erklärung auf der Basis des gesunden Menschenverstands habe. Es sei „hoffnungslos“ für jemanden, der sich in Entscheidungsbäumen und mit dem Satz von Bayes nicht auskenne, die Lösung zu verstehen. Als Vázsonyi von Erdős nach einer Stunde noch einmal gebeten wurde, ihm den Grund für den Wechsel zu nennen, führte er ihm schließlich eine Computersimulation vor. Laut Vázsonyi wandte Erdős ein, dass er den Grund immer noch nicht verstehe, er sei aber widerwillig überzeugt gewesen.
Einige Tage später teilte Erdős laut Vázsonyi mit, er habe die Lösung jetzt verstanden, nachdem ihm der Mathematiker Ronald Graham die Begründung für die Antwort gegeben habe. Vázsonyi schreibt jedoch, dass er selbst diese Begründung nicht verstand.
In seinem Buch über Paul Erdős gibt Paul Hoffmann Grahams Begründung wieder:[21] „Der Schlüssel zum Monty-Hall-Problem ist, dass man im Voraus weiß, dass der Moderator einem immer die Möglichkeit gibt, eine andere Tür zu wählen. Das gehört zu den Spielregeln und muss in die Betrachtungen einbezogen werden.“
Am Ende seines Artikels schreibt Vázsonyi im Abschnitt „Marilyn weiß es am besten“, dass er später durch einen Artikel zum Thema im Skeptical Inquirer aus dem Jahr 1991[22] einen tieferen Einblick in das Problem bekommen habe. In diesem Artikel, durch den auch Gero von Randow auf das Problem gestoßen war,[23] wird exakt die Originalaufgabe vos Savants aus dem Magazin Parade gestellt.
Die reale Spielshow
Wenn man die Frage Personen stellt, die die Show kennen, vermuten diese häufig, dass die Gewinnchancen für die Tore 1 und 2 gleich hoch seien. Als Grund dafür wird oft angegeben, dass man ja nichts über die Motivation des Showmasters wisse, das Tor 3 mit einer Ziege dahinter zu öffnen und einen Wechsel anzubieten. Es greife daher das Indifferenzprinzip.
Dieses Verständnis des Leserbriefs geht davon aus, dass es sich bei der Problemstellung um die Beschreibung einer einmaligen Spielsituation handelt, wie sie in der von Monty Hall moderierten Spielshow Let’s Make a Deal auftreten kann. Hier spielt der Showmaster (Moderator) eine aktive und unberechenbare Rolle. Im Gegensatz zu den Problemvarianten, in denen der Moderator auf einen an fixe Verhaltensregeln gebundenen „Handlanger“ reduziert wird, darf realistischerweise angenommen werden, dass er völlig frei in seinen Entscheidungen ist (Monty Hall: „Ich bin der Hausherr!“). Diese Freiheit kann anhand einiger Beispiele illustriert werden, wobei vor jedem Spiel Auto und Ziegen hinter den drei Toren zufällig neu verteilt wurden. Weil die Kandidaten diese Spielshow, für die sie sich als Teilnehmer beworben haben, kennen, ist ihnen die Unberechenbarkeit des Moderators natürlich bewusst.[12]
- Spiel 1
- Kandidat Alfred wählt Tor 1, der Moderator öffnet das Tor 1 mit einer Ziege dahinter; Alfred verliert.
- Spiel 2
- Kandidatin Berta wählt Tor 1, der Moderator öffnet Tor 2 mit einer Ziege dahinter und bietet Berta an, ihre Wahl zu ändern. Berta möchte wechseln, aber der Moderator öffnet kein Tor, sondern bietet 5000 Euro dafür, dass Berta bei ihrer ersten Wahl bleibt. Diese ändert ihre Wechsel-Entscheidung nicht, und der Moderator öffnet Tor 3 mit einer Ziege dahinter; Berta verliert.
- Spiel 3
- Kandidatin Conny wählt Tor 1, der Moderator öffnet kein Tor, sondern bietet der Kandidatin 1000 Euro dafür, dass sie auf das Öffnen des Tors verzichtet; Conny nimmt das Geld und gewinnt 1000 Euro.
- Spiel 4
- Kandidatin Doris wählt Tor 1, der Moderator öffnet daraufhin Tor 3 mit einer Ziege dahinter und bietet Doris an, ihre Wahl zu überdenken …
Angesichts der verschiedenen Verhaltensmöglichkeiten des Moderators sollte Doris ihre Gewinnchancen sorgfältig abwägen. Wenn sie glaubt, dass der Moderator nett zu ihr sei und sie von ihrer ersten falschen Wahl abbringen möchte, dann sollte sie wechseln. Wenn sie allerdings meint, dass ihr der Moderator nicht gut gesinnt sei und sie nur von ihrer ersten, richtigen Wahl ablenken möchte, dann sollte sie bei Tor 1 bleiben. Wenn Doris den Moderator nicht einschätzen kann – auch im Leserbrief werden keine entsprechenden Hinweise gegeben –, hat sie keine Möglichkeit, ihre Gewinnchance korrekt zu berechnen. Insbesondere kann sie sich nach dem Eingreifen des Moderators nicht mehr auf das Indifferenzprinzip berufen, und die Antwort auf die Frage „Ist es von Vorteil, die Wahl des Tores zu ändern?“ lautet in ihrem Fall also: „Nicht unbedingt.“
Obwohl die Frage des Leserbriefs damit bereits beantwortet ist, wurde der Vorschlag gemacht, Doris bei ihrer Entscheidung zu unterstützen und ihr eine echte 50:50-Chance auf den Gewinn zu verschaffen. Dazu wird angenommen, dass sie die Möglichkeit hat, sich nach dem Wurf einer fairen Münze für eines der beiden verbleibenden Tore zu entscheiden. Auf diese Weise kann sie sicherstellen, dass ihre Gewinnwahrscheinlichkeit unabhängig von den Absichten des Moderators genau 1⁄2 beträgt.[16]
Übersicht über die Fachliteratur zu „dem“ Ziegenproblem
Hinweise zur Literatur
In den Publikationen zum Ziegenproblem (Monty-Hall-Problem) werden, manchmal sogar innerhalb einer Publikation, unterschiedliche Fragestellungen und Modelle untersucht.[14][24]
Autoren wie Gill[24] und Krauss & Wang[1] sowie Krauss & Atmaca[8] legen ihrer Lösung vos Savants Originaltext zugrunde und machen ihre Zusatzannahmen erst im Laufe ihrer Analyse explizit. Dabei wird die Korrektheit von vos Savants Lösung, die die heftigen Kontroversen ausgelöst hatte, ausdrücklich herausgestellt.
Im Anhang von vos Savants Buch[4] schreibt Donald Granberg, es sei Konsens, dass vos Savants Antwort im Wesentlichen korrekt sei, vorausgesetzt, man mache sieben „hoch plausible“ Annahmen. Darunter befindet sich die Annahme, dass der Moderator verpflichtet ist, nach der ersten Wahl eine nichtgewählte Ziegentür zu öffnen, sowie die Annahme, dass der Moderator ehrlich ist.
Krauss & Wang[1] fügen der Aufgabe vos Savants, die sie als „Standardversion“ bezeichnen, mehrere Annahmen hinzu, damit sich die Lösung vos Savants präzise herleiten lässt. Auch in Krauss & Atmaca[8] wird mit dem Originalproblem vos Savants begonnen, wobei der Moderator, bevor er die Ziegentür öffnet, entsprechend der Formulierung Gero von Randows[23] noch sagt Ich zeige Ihnen mal was. Nach Steinbach[16] sind diese Worte des Moderators aus der Sicht des Kandidaten „unsinnig“, wenn er auf Grund der Spielregeln sowieso erwartet, eine Ziege gezeigt zu bekommen. Auch Henze[25] lässt in seiner Aufgabenformulierung den Moderator, bevor er die Ziegentür öffnet, sagen Soll ich Ihnen mal was zeigen?, und schreibt, nachdem er die Lösung vos Savants als korrekt dargestellt hat: Bei allen diesen Betrachtungen ist natürlich entscheidend, dass der Moderator die Autotür geheimhalten muss, aber auch verpflichtet ist, eine Ziegentür zu öffnen. In einer Vorlesung im Sommersemester 2014[26] schreibt er diesen Zusatz zu Beginn in die Aufgabenstellung und stellt ausführlich heraus, dass vos Savant recht hatte.
Lucas[14] verwendet eine Problemformulierung, die dem Moderator von vornherein gewisse Verhaltensregeln vorschreibt. Bei der Beurteilung der heftigen Reaktionen auf vos Savants Lösung spielt es für Lucas[14] jedoch keine Rolle, dass diese Verhaltensregeln in dem von vos Savant vorgelegten Problem nicht formuliert worden waren.
Morgan et al.[13] sowie Gill[24] wiederum thematisieren nicht, dass in vos Savants Originalfragestellung die Regel fehlte, dass der Moderator verpflichtet ist, nach der ersten Wahl eine nicht gewählte Ziegentür zu öffnen und einen Wechsel anzubieten. Den einzigen Fehler in vos Savants Lösung sehen Morgan et al. darin, dass sie nicht explizit angenommen hat, dass der Moderator dann, wenn der Kandidat die Autotür gewählt hat, beide möglichen Ziegentüren mit gleicher Wahrscheinlichkeit öffnet. Erst nach ihren Ausführungen zu Aufgabe und Lösung erwähnen Morgan et al. und Gill andere Möglichkeiten des Spielablaufs. Morgan et al. gehen nun sogar davon aus, dass der Moderator, ohne den Spieler zu informieren, auch die Autotür öffnen darf, was bei einem „plausiblen Szenario“ zur „populären Antwort 1⁄2“ für den Fall führe, dass er eine nicht gewählte Ziegentür öffnet. Sie schreiben sogar, dass es die Perspektive des Moderators verlangt, das „vos-Savant-Szenario“ nicht zu befolgen, um Spieler davon abzuhalten, immer zu wechseln. Dem Moderator zu erlauben, sofort auch die vom Kandidaten gewählte Tür zu öffnen, nennen sie eine „Verallgemeinerung“, die an den Betrachtungen der bedingten Wahrscheinlichkeiten nichts ändere.
Götz (2006)[27] sieht „das berühmte ‚Ziegenproblem‘“ als „hinreichend diskutiert“ an. In seiner Beschreibung der Problemstellung heißt es: Jetzt kommt der entscheidende Punkt. Der Spielleiter fragt die Kandidatin, ob sie bei ihrer ursprünglichen Wahl der Türe bleiben möchte oder auf die andere, noch geschlossene Türe wechseln möchte. Zur Lösung schreibt er, dass die Strategie „Wechseln“ mit Wahrscheinlichkeit 2⁄3 zum Auto führt. Nach verschiedenen Lösungsansätzen erwähnt er, dass „R. Grothmann (2005)“ darauf hingewiesen habe, dass es klar sein muss, ob der Spielleiter eine nicht gewählte Tür öffnen muss oder auch die gewählte öffnen kann.
„Das aus den Medien bekannte umstrittene Ziegenproblem“ wird von Steinbach[16] „vollständig analysiert und gelöst“. Dabei geht er von Gero von Randows[23] Problemformulierung aus. Steinbach vermutet, dass die unterschiedlichen Antworten auf die Originalfrage darauf zurückzuführen sind, dass die Befürworter der 2⁄3-Lösung die Perspektive des „Denksportlers“, die Befürworter der Lösung 1⁄2 die des Kandidaten einnehmen: Allein aus den Worten des Moderators und dem Anblick der Ziege kann der Kandidat nämlich nicht erkennen, ob irgendeine Spielregel gilt – und schon gar nicht, welche. […] Es bleibt nur der Münzwurf: so erwischt der Kandidat – unabhängig vom Verhalten des Moderators! – mit Wahrscheinlichkeit 1⁄2 die richtige Tür.
Gigerenzer und Grams stellen heraus, dass ein Großteil der Debatte zum Ziegenproblem darauf zurückgeht, dass von den Autoren nicht ausreichend zwischen „Entscheidung bei Risiko“ und „Entscheidung bei Ungewissheit“ unterschieden wird: „Unter den Tausenden von Artikeln, die über das Monty-Hall-Problem veröffentlicht wurden, blieb der Unterschied zwischen Risiko und Ungewissheit praktisch unbeachtet“ (Gigerenzer).
Die Fragestellung ist qualitativ, nicht quantitativ
In Bezug auf die verschiedenen Lösungen, wie sie auch oben wiedergegeben wurden, resümiert Götz „WECHSELN IST NIE SCHLECHTER ALS BLEIBEN!“ (Versalien gemäß Referenz).[27] Auf diesen Sachverhalt hatten bereits 1991 Morgan et al., die „Entdecker“ der auf Zusatzannahmen über das Moderatorverhalten basierenden Lösungen, aufmerksam gemacht.[13] Trotz dieser qualitativen Übereinstimmung und der Tatsache, dass die Problemstellung „Ist es von Vorteil, die Wahl des Tores zu ändern?“ nach einer Aktion und nicht nach einer Wahrscheinlichkeit fragt,[24] sind die Annahmen, die zu unterschiedlichen Wahrscheinlichkeitswerten führen, immer wieder Gegenstand heftiger Diskussionen. So enthält allein die Bibliografie des 2009 erschienenen Buchs The Monty Hall Problem von Rosenhouse über hundert Veröffentlichungen.[28]
Frequentistische Sicht
Georgii[15] kommt zunächst unter der Annahme, dass der Moderator nach der ersten Wahl des Kandidaten zum Öffnen einer nicht gewählten Ziegentür verpflichtet ist, unmittelbar zur Gewinnwahrscheinlichkeit 2⁄3 bei einem Türwechsel. Die „Trivialität“ dieser Lösung, die genau der Antwort vos Savants entspricht, liegt nach Georgii daran, dass wir den Moderator auf eine feste Verhaltensweise festgelegt haben, dass er also das Spiel immer so durchführt wie beschrieben. Den „tieferen Grund“ für diese Festlegung sieht er darin, dass wir implizit von einer frequentistischen Interpretation der bedingten Wahrscheinlichkeiten ausgegangen sind, welche die Wiederholbarkeit des Vorgangs und also feste Regeln voraussetzt. Entsprechend der Bemerkung von Morgan et al.[13] die Perspektive des Moderators verlange es, das „vos-Savant-Szenario“ nicht zu befolgen, schreibt auch Georgii: Nun wird der Moderator das Spiel aber nicht regelmäßig durchführen. Unter diesem Gesichtspunkt sei die „subjektive Interpretation“ angemessener. Als Beispiel nennt er dann die Variante mit Gewinnwahrscheinlichkeit 1⁄2, bei der der Moderator vor dem Wechselangebot mit gleicher Wahrscheinlichkeit eine der beiden Ziegentüren öffnet, unabhängig davon, welche Tür der Spieler gewählt hat. (Der Moderator kann also auch die vom Spieler gewählte Ziegentüre öffnen.) Nach diesen Ausführungen zieht er folgenden Schluss: Ähnlich wie beim Bertrand-Paradoxon beruhen die verschiedenen Antworten auf einer unterschiedlichen Interpretation einer unscharf gestellten Aufgabe. […] Die philosophische Unsicherheit über die Bedeutung bedingter Wahrscheinlichkeiten kommt dabei erschwerend hinzu.
Einfluss des Moderatorverhaltens bei Wahl der Autotür
Die Bemerkung Georgiis,[15] dass es darauf ankomme, „wie der Spieler das Verhalten des Moderators einschätzt“, lässt sich auch anwenden auf die Frage, mit welcher Wahrscheinlichkeit der Moderator eine bestimmte Ziegentür öffnet, wenn der Kandidat die Autotür gewählt hat. Die meisten Lehrbuchautoren verzichten allerdings auf die Berücksichtigung einer solchen subjektiven Einschätzung des Moderatorverhaltens. Konkret gehen sie davon aus, dass der Moderator ausgeglichen agiere, das heißt, dass er die Auswahl des Tors gemäß einer Gleichverteilung vornimmt. Dadurch wird dieser Ansatz zur häufigsten in der Fachliteratur vertretenen Erklärung dafür, dass ein Torwechsel mit der Wahrscheinlichkeit von 2⁄3 zum Gewinn führt.[10][25][29][30][31] Diese Gewinnwahrscheinlichkeit von 2⁄3 bei einem Torwechsel bezieht sich explizit auf den Zeitpunkt nach dem Öffnen eines Tores durch den Moderator.
Untersuchungen, bei denen der Kandidat den Moderator auch dahingehend einschätzt, seine Torauswahl nicht gleichwahrscheinlich vorzunehmen, wurden erstmals 1991 von Morgan et al.[13] und unabhängig davon 1992 von Gillmann[32] veröffentlicht. Dabei haben Morgan et al.[13] vos Savants Aufgabe so abgeändert, dass sich die Fragestellung genau auf die genannten Türnummern bezog, die bei vos Savant nur als erläuternde Beispiele vorkamen. Die Variante vos Savants mit einer Million Türen bezeichneten Morgan et al.[13] als „dubiose Analogie“. Die Anwendung des Verfahrens von Morgan et al.[13] auf diese Variante liefert ohne Zusatzannahmen dasselbe Ergebnis wie bei nur drei Türen, nämlich einen Wert zwischen 1⁄2 und 1 – gegenüber 99,9999 % bei vos Savant.
In ihrer Erwiderung[33] auf Morgan et al. weist vos Savant auf die verkürzte Wiedergabe sowohl ihrer Fragestellung als auch ihrer Antwort hin, deren vollständige Version sie in ihrem Antwortbrief wiedergibt. Morgan et al.[33] wiederum antworten darauf, dass in dieser Darstellung der Hinweis fehle, dass die Fragestellung von einem „Leser in Columbia, Maryland“ stamme. Das sei deshalb wichtig, weil die Einschränkung, „dass der Moderator eine Ziege zeigen muss“, von vos Savant selbst hinzugefügt worden sei. Vos Savant selbst hat darauf hingewiesen, dass sie den Eindruck hatte, dass diese „bedeutendste“ einschränkende Bedingung in der ursprünglichen Leserfrage nicht genügend hervorgehoben worden war und dass sie sie deshalb in ihrer Antwort hinzugefügt habe.[4]
Bei den anderen in ihrer ursprünglichen Fragestellung nicht formulierten Voraussetzungen bleibt sie bei ihrer Auffassung, dass sie ihr für ein allgemeines Verständnis des Problems nicht wichtig erscheinen, da Ereignisse standardmäßig als „zufällig“ betrachtet werden.[33] Diese Auffassung teilt auch Steinbach,[16] der diese Annahmen, bevor er sie unter der Überschrift „Haarspaltereien“ mathematisch untersucht, als „stillschweigend, aber unstrittig und irrelevant“ bezeichnet.
Bayessche Sicht
Nach Georgii reduzieren sich die unterschiedlichen Standpunkte zu der „unscharf gestellten Aufgabe“ auf die Frage, ob es Bestandteil einer festen Spielregel ist, dass der Moderator eine nicht gewählte Ziegentür öffnen und einen Wechsel anbieten muss.[15]
Während bei Georgii die Frage, mit welcher Wahrscheinlichkeit der Moderator eine bestimmte Ziegentür öffnet, wenn der Kandidat die Autotür gewählt hat, nicht thematisiert wird und für seine Lösung keine Rolle spielt, verweist Götz dazu auf zwei „unterschiedliche Wahrscheinlichkeitsbegriffe, die den jeweiligen Betrachtungsweisen zugrunde liegen.“ Die „klassische Lösung“ ohne die Betrachtung dieses Moderatorverhaltens sei „frequentistisch“ zu deuten und empirisch zu überprüfen. Demgegenüber liefere eine „Bayesianische Lösung […] die Bewertungsgrundlage einer Einzelsituation. Wie soll sich die Kandidatin hic et nunc verhalten, nachdem der Spielleiter eine Tür geöffnet hat? […] Man fragt also nach Zustandswahrscheinlichkeiten oder Erkenntniswahrscheinlichkeiten (und nicht nach Wahrscheinlichkeiten zukünftiger Zufallsereignisse).“[27] Mit anderen Worten: Die Kandidatin macht nach der Toröffnung durch den Moderator die Bewertung seiner beiden Handlungsoptionen davon abhängig, welches grundsätzliche Verhalten sie dem Moderator unterstellt. Dabei wird der Extremfall eines faulen Moderators durch die Antwort auf die folgende Frage charakterisiert: „Hätte der Moderator, nachdem er meine Entscheidung für ein Tor gesehen hat, das von ihm gerade geöffnete Tor auch unter allen anderen Umständen ausgewählt, sofern es ihm nur möglich – kein Auto dahinter – gewesen wäre?“
Wenn die Kandidatin nichts über die Vorlieben des Moderators weiß, „bringt Wechseln“ laut Götz „eine Erfolgschance von 2⁄3“. Gute Schätzwerte für den unbekannten Parameter p erhalte man durch Beobachten des Verhaltens des Spielleiters in der passenden Situation, wenn das Auto hinter Tür 1 steht und die Kandidatin ebendiese Tür (zunächst) erwählt hat.
Bayessche Untersuchungen wurden erstmals von Morgan et al.[13] durchgeführt, und zwar auf Basis ihrer Ergebnisse, bei denen der Moderator das zu öffnende Tor zufällig gemäß dafür angenommener A-priori-Wahrscheinlichkeiten auswählt.
Vergleich der verschiedenen Lösungen
Nummerierung der Tore
Die im letzten Abschnitt vorgenommene Charakterisierung des Verhaltens eines faulen Moderators zeigt, dass eine diesbezügliche Lösung nicht an eine Nummerierung der Tore gebunden ist (üblicherweise „Kandidat wählt Tor 1. Moderator öffnet Tor 3, wenn immer es möglich ist“).[24]
Empirische Überprüfung einer auf das Moderatorverhalten bezogenen Lösung
Soll beispielsweise die für die Variante eines faulen Moderators gefundene 50:50-Lösung empirisch geprüft werden, so ist dabei zu berücksichtigen, dass sich die auf dieser Basis hergeleitete Aussage auf ein bedingtes Ereignis bezieht. Bei einer Versuchsreihe von 300 Spielshows, die gemäß der Zusatzannahme fauler Moderator durchgeführt werden, durchlaufen damit ungefähr 100 Shows nicht das Ereignis, das Gegenstand der Untersuchung ist. Konkrete Ursache dafür ist, dass bei einem hinter Tor 3 verborgenen Auto der Moderator gezwungen ist, Tor 2 zu öffnen. Solche Spielverläufe liegen aber außerhalb des Untersuchungsbereichs, so dass die nach einem Torwechsel stets erzielten Gewinne bei der Versuchsreihenauswertung unberücksichtigt bleiben müssen.[13]
Entscheidungssituationen mit unterschiedlichen Gewinnchancen

Die „global“ für alle denkbaren Entscheidungssituationen festgelegte Torwechsel-Strategie bringt insgesamt einen 2:1-Vorteil. Allerdings können durch einen asymmetrischen Spielverlauf Entscheidungssituationen entstehen, bei denen ein Torwechsel gegenüber dem Durchschnitt aussichtsreicher beziehungsweise weniger aussichtsreich ist. Solche Effekte sind im Hinblick auf eine asymmetrische Wahrscheinlichkeitsverteilung bei der Auslosung des Gewinntors offensichtlich,[34] aber sie können, wie die Ergebnisse für den faulen Moderator zeigen, auch durch ein asymmetrisches Moderatorverhalten verursacht werden. Beim Moderatorverhalten sind allerdings die möglichen Abweichungen für die Gewinnwahrscheinlichkeit beim Torwechsel vom A-priori-Wert 2⁄3 nach unten begrenzt, da der Wert 1⁄2 nicht unterschritten werden kann, denn „Wechseln ist nie schlechter als Bleiben“ – siehe oben.
Die beiden einen 2:1-Vorteil prognostizierenden Lösungen
Auch wenn die „klassische“ vos-Savant-Lösung übereinstimmend mit der Lösung für den ausgeglichenen Moderator für einen Torwechsel einen 2:1-Vorteil vorhersagt, sind ihre Betrachtungswinkel und Argumente doch sehr unterschiedlich: Einmal wird eine A-priori-Wahrscheinlichkeit für die Situation unmittelbar vor der Entscheidung des Moderators für ein zu öffnendes Tor angegeben. Das andere Mal bezieht sich die Wahrscheinlichkeit auf den Zeitpunkt, wenn der Moderator „sein“ Tor bereits geöffnet hat, wobei allerdings die Zusatzannahme gemacht wird, dass der Moderator seine Auswahl gleichwahrscheinlich getroffen hat. Der Umstand, dass beide Ansätze die gleiche Gewinnwahrscheinlichkeit liefern, folgt aus einer Symmetriebetrachtung, die den A-posteriori-Wert aus dem A-priori-Wert herleitet.[24]
Spieltheoretischer Ansatz
Mit unterschiedlichen Annahmen über die Wahrscheinlichkeit, mit der der Moderator eine bestimmte Ziegentür öffnet, wenn der Kandidat die Autotür gewählt hat, lassen sich für den jeweiligen Einzelfall auch unterschiedliche Gewinnwahrscheinlichkeiten errechnen. Dieser Aspekt wurde von einigen Autoren als Ausgangspunkt spieltheoretischer Untersuchungen des Ziegenproblems genommen. Dabei wird die Zusatzannahme über diese Wahrscheinlichkeit als gemischte Strategie im Sinne eines Zwei-Personen-Spiels aufgefasst,[24][35] das sogar Nullsummencharakter besitzt. Einbezogen in den sequentiellen Spielablauf wird auch das Verstecken des Autos, das als erster Zug des Moderators gewertet wird. Mit einem einfachen Argument, das für beide Spieler naheliegende, in Bezug auf die Tore symmetrische Strategien verwendet, konnte Gill zeigen, dass der Minimax-Wert 2⁄3 beträgt.[24]
Die Menge der Minimax-Strategien für beide Spieler wurde von Gnedin bestimmt.[36] Dabei besitzt der Kandidat nur eine einzige Minimax-Strategie, bei der er sein zuerst gewähltes Tor gemäß einer Gleichverteilung auslost und anschließend immer das Tor wechselt. Die Aussage ist insofern bemerkenswert, da sie ohne A-priori-Annahme über das Verhalten des Moderators auskommt und trotzdem Aussagen für jede einzelne im Spiel auftauchende Entscheidungssituation macht. Ein noch stärkeres Argument für den Kandidaten, nie das anfangs gewählte Tor beizubehalten, ergibt sich aus Gnedins Dominanz-Analysen für Strategien.
Weitere mathematisch untersuchte Varianten
Neben den oben dargestellten Interpretationen „des“ Ziegenproblems gibt es noch weitere Varianten, die in der Fachliteratur untersucht wurden. Generell ist dazu anzumerken, dass bei den Autoren – wie schon im Hinblick auf die oben dargestellten Interpretationen – kein Konsens darüber besteht, welches mathematische Modell „dem“ Ziegenproblem und seiner Fragestellung entspricht. Teilweise dienen die Modelle auch nur dem Zweck eines erläuternden Vergleichs:
Moderator kann auch das Tor mit dem Auto öffnen
Lucus, Rosenhouse, Madison und Schepler[14] sowie Morgan et al.[13] analysieren unter anderem auch die Variante, bei der der Moderator sein Tor zufällig unter den beiden verbliebenen Toren wählt und dabei gegebenenfalls auch das Tor mit dem Auto öffnet. Eine kurze Berechnung bestätigt die auch intuitiv naheliegende Vermutung, dass für diese Variante in dem Fall, dass ein Tor mit Ziege geöffnet wird, die Gewinnwahrscheinlichkeit beim Wechseln 1⁄2 beträgt.
Moderator kann auch das zuerst gewählte Tor öffnen
Georgii lässt in einer der zwei von ihm untersuchten Varianten auch zu, dass der Moderator das zuerst vom Spieler gewählte Tor mit einer Ziege öffnet. Wenn der Moderator dabei zufällig mit gleicher Wahrscheinlichkeit zwischen den beiden Ziegentoren auswählt, beträgt die Gewinnwahrscheinlichkeit bei einem Wechsel entsprechend der „Antwort der Kritiker“ auch dann 1⁄2, wenn er ein nicht gewähltes Ziegentor öffnet.[15]
Das Ziegenproblem in den Medien
Das US-amerikanische Filmdrama 21 (2008) thematisiert das Ziegenproblem als Aufreißer für eine von zwei mathematischen Strategien, mit denen im Verlauf des Films große Geldsummen beim Black-Jack-Spielen erbeutet werden.
Jamie Hyneman und Adam Savage untersuchen in Episode 177 Mythen ohne Ende ihrer Dokumentarserie Mythbusters das Ziegenproblem. Dabei wurden die beiden Behauptungen, dass (1) Personen dazu neigen, bei ihrer ersten Wahl zu bleiben und (2) dass das Ändern der ursprünglichen Entscheidung die Gewinnchance signifikant erhöht, bestätigt.[37]
Auch in der achten Episode („Drachen haben Lümmel“) der vierten Staffel der Fernsehserie Brooklyn Nine-Nine wird das Problem erklärt und behauptet, die Lösung des Problems sei einfach, da die zweite Option (Ändern der ursprünglichen Entscheidung) die einzig logische Antwort sei.
Einfluss von Wikipedia
Im Rahmen ihrer Mitarbeit bei Wikipedia fanden W. Nijdam und Martin Hogbin 2010 einen Fehler in der damals knapp 20 Jahre alten Arbeit von Morgan et al.[24][13][38] Demnach ist, wenn eine nicht-informative A-priori-Verteilung für das Moderatorverhalten zugrunde gelegt wird, die Gewinnwahrscheinlichkeit beim Torwechsel 2⁄3 und nicht , wie Morgan et al. berechnet hatten. Die Bestätigung dieses Sachverhalts nutzten Morgan et al., um erstmals die originale Fragestellung aus Craig F. Whitakers Leserbrief an Marilyn vos Savant zu veröffentlichen.
Siehe auch
- Gefangenenparadoxon
- Problem der 100 Gefangenen
- Geburtstagsparadoxon
Literatur
Bücher
- Gero von Randow: Das Ziegenproblem – Denken in Wahrscheinlichkeiten. Rowohlt, Reinbek 1992, ISBN 3-499-19337-X, Neuauflage: Rowohlt, Reinbek 2004, ISBN 3-499-61905-9.
- Jason Rosenhouse: The Monty Hall Problem. Oxford University Press 2009, ISBN 978-0-19-536789-8.
Buchkapitel
- Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen. Springer Spektrum, 7. Auflage 2018, ISBN 978-3-658-21764-8, doi:10.1007/978-3-658-21765-5, S. 34–38, 334–345.
- Hans-Otto Georgii: Stochastik, Einführung in Wahrscheinlichkeitstheorie und Stochastik. de Gruyter 2004, 5. Auflage 2015, ISBN 978-3-11-035970-1, doi:10.1515/9783110359701, S. 61–64 (Auszug (Google))
- Gerd Gigerenzer: Das Einmaleins der Skepsis – Über den richtigen Umgang mit Zahlen und Risiken. Berlin-Verlag, Berlin 2002, ISBN 3-8270-0079-3.
- Gerd Gigerenzer: Risiko. Wie man die richtigen Entscheidungen trifft. C. Bertelsmann, München 2013, ISBN 978-3-570-10103-2.
- Timm Grams: Klüger irren – Denkfallen vermeiden mit System. Springer, Berlin / Heidelberg 2016, ISBN 978-3-662-50279-2, doi:10.1007/978-3-662-50280-8, S. 186–197.
- Charles M. Grinstead, J. Laurie Snell: Grinstead and Snell’s Introduction to Probability. 4. Juli 2006, S. 136–139 (englisch, math.dartmouth.edu [PDF; abgerufen am 2. April 2008] Online version of Introduction to Probability, 2nd edition, American Mathematical Society, Copyright (C) 2003 Charles M. Grinstead and J. Laurie Snell).
- Norbert Henze: Stochastik für Einsteiger. 12. Auflage, Springer Spektrum 2018, ISBN 978-3-658-22044-0, doi:10.1007/978-3-658-22044-0, S. 48, 100–106. (Auszug (Google) der 8. Aufl.)
- Henk Tijms: Understanding Probability, Chance Rules in Everyday Life. University Press, 2nd edition, Cambridge 2007, ISBN 978-0-521-70172-3, doi:10.1017/CBO9780511619052. S. 15 f., 206–220.
Artikel
- Christoph Drösser: Der maliziöse Moderator. Die Zeit, 22. Juli 2010
- Christoph Drösser: Und ewig meckert die Ziege. Die Zeit, 19. August 2011
- Sasha Gnedin: The Mondee Gills Game. In: The Mathematical Intelligencer, 2011, doi:10.1007/s00283-011-9253-0 (OpenAccess).
- Jochen Paulus: Das Rätsel der drei Türen. Die Zeit, 18. November 2004
- Marc C. Steinbach: Autos, Ziegen und Streithähne. Mathematische Semesterberichte (2000) 47/1, doi:10.1007/s005910070014, S. 107–117, Preprint.
Weblinks
- Matheprisma der Uni Wuppertal: Ziegenproblem: Online Simulation, bedingte und totale Wahrscheinlichkeit, Bayes-Formel
- Gerhard Keller: Ein Auto und zwei Ziegen. Zur Rezeptionsgeschichte des Ziegenproblems.
Einzelnachweise
- ↑ a b c Stefan Krauss, X. T. Wang:The Psychology of the Monty Hall Problem: Discovering Psychological Mechanisms for Solving a Tenacious Brain Teaser. ( vom 30. Mai 2009 im Internet Archive) In: Journal of Experimental Psychology: General. 132 (1)2003.
- ↑ a b c d Craig F. Whitaker: Ask Marilyn. In: Parade Magazine. 9. September 1990, S. 16.
- ↑ a b c Game-Show-Problem ( vom 10. März 2010 im Internet Archive) – gesammelte Leserbriefe und Antworten innerhalb des Webauftritts von Marilyn vos Savant
- ↑ a b c d Marilyn vos Savant: Brainpower – Die Kraft des logischen Denkens. Rowohlt Verlag GmbH, 2001, ISBN 3-499-61165-1
- ↑ a b Peter R. Mueser, Donald Granberg:The Monty Hall Dilemma Revisited: Understanding the Interaction of Problem Definition and Decision Making. ( vom 22. Juli 2012 im Internet Archive) In: University of Missouri Working Paper. 1999-06.
- ↑ a b c d e f g h Jeffrey S. Rosenthal: Monty Hall, Monty Fall, Monty Crawl. (PDF; 70 kB) In: Math Horizons. September 2008, S. 5–7.
- ↑ a b Richard Williams: "Appendix D: The Monty Hall Controversy" (PDF) In:"Course notes for Sociology Graduate Statistics" 2004
- ↑ a b c d S. Krauss, S. Atmaca: Wie man Schülern Einsicht in schwierige stochastische Probleme vermitteln kann. Eine Fallstudie über das „Drei-Türen-Problem“. In: Unterrichtswissenschaft, 2004, 1, S. 38–57, online
- ↑ Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen. Springer Spektrum, 6. Auflage 2012, ISBN 978-3-8348-1923-9, doi:10.1007/978-3-8348-2319-9, S. 34–38.
- ↑ a b c Ehrhard Behrends: Fünf Minuten Mathematik, Vieweg, 1. Auflage 2006, ISBN 978-3-8348-0082-4, doi:10.1007/978-3-8348-9013-9, S. 32–39
- ↑ Bei vorgestellter Erweiterung des Spiels um zusätzliche Türen hätte der Spieler im Allgemeinen mehrere Türen zur Auswahl, zu denen er wechseln könnte. Die bedingten Wahrscheinlichkeiten und nähmen dann Werte größer als 0 und kleiner als 1 an, so dass sie intuitiver als Wahrscheinlichkeiten wahrnehmbar wären. Das hier behandelte Drei-Türen-Spiel verwirklicht so gesehen den Grenzfall mit einem Auto, einer enthüllten und einer verborgenen Ziege. Siehe: Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen. Springer Spektrum, 7. Auflage 2018, ISBN 978-3-658-21764-8, doi:10.1007/978-3-658-21765-5, S. 37 f.
- ↑ a b c d e John Tierney: Behind Monty Hall’s Doors: Puzzle, Debate and Answer? In: The New York Times. 21. Juli 1991.
- ↑ a b c d e f g h i j k l m J. P. Morgan, N. R. Chaganty, R. C. Dahiya and M. J. Doviak: Let’s Make a Deal: The Player’s Dilemma. In: The American Statistician, Band 45, Heft 4, 1991, S. 284–287 (JSTOR:2684453)
- ↑ a b c d e Stephen Lucas, Jason Rosenhouse, James Madison, Andrew Schepler: The Monty Hall Problem, Reconsidered. In: Mathematics Magazine, Band 82, Heft 5, 2009, S. 332–342, JSTOR:27765931, Preprint (PDF; 110 kB), Nachdruck in: Michael Henle, Brian Hopkins (Hrsg.): Martin Gardner in the Twenty-First Century, 2011, ISBN 978-0-88385-913-1, S. 231–242
- ↑ a b c d e Hans-Otto Georgii: Stochastik, 4. Auflage, de Gruyter, 2009, ISBN 978-3-11-021526-7, doi:10.1515/9783110215274, S. 56–58, Auszug Google Books
- ↑ a b c d e Marc C. Steinbach: Von Autos, Ziegen und Streithähnen. (PDF; 228 KB) Kapitel 4.2
- ↑ Steve Selvin: 1. Leserbrief. The American Statistician (Februar 1975) (JSTOR)
- ↑ Steve Selvin: 2. Leserbrief. Excerpted from The American Statistician (August 1975)
- ↑ Jason Rosenhouse: The Monty Hall Problem. Oxford University Press 2009, ISBN 978-0-19-536789-8, S. IX, 20–26.
- ↑ Andrew Vázsonyi: The Real-Life Adventures of a Decision Scientist, Which Door Has the Cadillac?. In: Decision Line, December/January 1999;decisionsciences.org ( vom 9. März 2014 im Internet Archive)
- ↑ Paul Hoffman: The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. Hyperion, 1998.
- ↑ Skeptical Inquirer, Vol. 15, Summer 1991, S. 342–345; gpposner.com
- ↑ a b c Gero von Randow: Das Ziegenproblem – Denken in Wahrscheinlichkeiten. Rowohlt, Reinbek 1992, ISBN 3-499-19337-X, Neuauflage: Rowohlt, Reinbek 2004, ISBN 3-499-61905-9.
- ↑ a b c d e f g h i Richard D. Gill: The Monty Hall problem is not a probability puzzle (it’s a challenge in mathematical modelling). Statistica Neerlandica, Band 65, Heft 1, 2011, S. 58–71, doi:10.1111/j.1467-9574.2010.00474.x, arxiv:1002.0651.
- ↑ a b Norbert Henze: Stochastik für Einsteiger: Eine Einführung in die faszinierende Welt des Zufalls. Vieweg+Teubner Verlag, 2010, ISBN 978-3-8348-0815-8, doi:10.1007/978-3-8348-9351-2, S. 51–52, 98, 104–106
- ↑ Norbert Henze: Einführung in die Stochastik für Studierende des gymnasialen Lehramts Mathematik. Vorlesung, Lektion 5, 2. Mai 2014 (SS2014);
- ↑ a b c Stefan Götz: Ziegen, Auto und Bayes – eine never-ending story. In: Stochastik in der Schule, Band 26, Heft 1, 2006, S. 10–15,math.uni-paderborn.de ( vom 4. Januar 2014 im Internet Archive) (PDF)
- ↑ Jason Rosenhouse: The Monty Hall Problem. Oxford University Press, 2009, ISBN 978-0-19-536789-8
- ↑ Jörg Rothe, Dorothea Baumeister, Claudia Lindner, Irene Rothe: Einführung in Computational Social Choice: Individuelle Strategien und kollektive Entscheidungen beim Spielen, Wählen und Teilen. Spektrum Akademischer Verlag, 2012, ISBN 978-3-8274-2570-6, doi:10.1007/978-3-8274-2571-3, S. 65–69
- ↑ Rick Durett: Elementary Probability for Applications. 2009, ISBN 978-0-521-86756-6, S. 84–85
- ↑ Charles M. Grinstead, J. Laurie Snell: Introduction to probability. 2nd edition. American Mathematical Society, 2003,dartmouth.edu ( vom 10. November 2013 im Internet Archive) (PDF), S. 136–139.
- ↑ Leonard Gillman: The Car and the Goats. The American Mathematical Monthly, Band 99, Heft 1, 1992, S. 3–7 (JSTOR:2324540)
- ↑ a b c The American Statistician, November 1991, Vol. 45, No. 4, S. 347; doi:10.1080/00031305.1991.10475834.
- ↑ Jason Rosenhouse: The Monty Hall Problem. Oxford University Press, 2009, ISBN 978-0-19-536789-8, S. 78–80
- ↑ Richard D. Gill: Monty Hall problem: solution. In: International Encyclopedia of Statistical Science, S. 858–863, Springer, 2011, ISBN 978-3-642-04897-5, doi:10.1007/978-3-642-04898-2, arxiv:1002.3878v2.
- ↑ Sasha Gnedin: The Mondee Gills Game. The Mathematical Intelligencer, Band 34, Heft 1, S. 34–41, doi:10.1007/s00283-011-9253-0
- ↑ „Mythen ohne Ende“ (orig. „Wheel of Mythfortune“), Jamie Hyneman und Adam Savage, „Mythbusters“, Staffel 9, Episode 21, zuerst ausgestrahlt am 23. November 2011
- ↑ J. P. Morgan, N. R. Chaganty, R. C. Dahiya, M. J. Doviak: Let’s Make a Deal: The Player’s Dilemma. In: The American Statistician, 1991, 45 (4), S. 284–287. Comment by Hogbin and Nijdam and Response. In: The American Statistician, Band 64, Heft 2, 2010, S. 193–194, doi:10.1198/tast.2010.09227
Auf dieser Seite verwendete Medien
Monty Hall paradox illustration
Autor/Urheber: HilberTraum, Lizenz: CC BY-SA 3.0
Simulation des Ziegenproblems, bedingte (rot) und unbedingte (blau) Häufigkeiten
Autor/Urheber: Buecherdiebin, Lizenz: CC0
Illustration for Monty Hall problem showing the standard probabilities of "stay" and "switch" with German description. Original version with English description created by Rick Block.