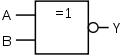XNOR-Gatter

Ein XNOR-Gatter (engl. eXclusive NOT OR) ist ein Logikgatter, bei dem am Ausgang eine logische „1“ anliegt, wenn an einer geraden Anzahl von Eingängen „1“ anliegt und an den restlichen „0“. Im Fall von zwei Eingängen liegt am Ausgang also „1“ an, wenn an beiden Eingängen „1“ oder an beiden Eingängen „0“ anliegt (im zweiten Fall liegt an null Eingängen „1“ an, und 0 zählt als gerade Zahl). Die XNOR-Verknüpfung wird auch als Äquivalenz, Biimplikation oder Bikonditional bezeichnet. Es bildet zusammen mit dem XOR einen booleschen Ring ab, so wie AND mit OR und NAND mit NOR.

Übersicht

Funktion	Schaltsymbol			Wahrheitstabelle	Relais-Logik
	IEC 60617-12	US ANSI 91-1984	DIN 40700 (vor 1976)
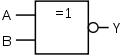${\displaystyle Y={\overline {A\,{\underline {\lor }}\,B}}}$ ${\displaystyle Y=A\,{\overline {\underline {\lor }}}\,B}$ ${\displaystyle Y={\overline {A\oplus B}}}$ ${\displaystyle Y=(A\land B)\lor ({\overline {A}}\land {\overline {B}})}$			oder	A B Y = A XNOR B 0 0 1 0 1 0 1 0 0 1 1 1

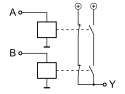
Logiksynthese

Realisierung mittels NAND oder NOR

Umsetzung mit NAND	Umsetzung mit NOR

XOR und Inverter

Das XNOR-Gatter lässt sich auch durch ein Exklusiv-Oder-Gatter mit nachgeschaltetem Nicht-Gatter (Inverter) aufbauen.

AND-OR-Invert

Ein XNOR-Gatter kann mit einem NAND-Gatter mit einem nachgeschalteten OR-AND-Invert-Gatter realisiert werden. Alternativ, wenn sowohl die Ausgangssignale als auch die invertierten Signale zur Verfügung stehen (beispielsweise die Ausgänge eines Flipflops), kann es aus einem 2-2-AND-OR-Invert-Gatter aufgebaut werden.^[1]

• 
  XNOR-Implementierung mit einem NAND- und einem OAI-Gatter
• 
  XNOR-Implementierung mit normalen und invertierten Eingängen aus einem 2-2-AND-OR-Invert-Gatter

CMOS

Mit den oben dargestellten Schemata lasen sich NAND-Gatter in CMOS realisieren, unter Verwendung von 10 bzw. 8 Transistoren.^[1] Stehen die invertierten Eingänge nicht zur Verfügung, so sind vier weitere Transistoren für die Inverter erforderlich.

• 
  Ein XNOR-Gatter in CMOS mit einem NAND- und einen OAI-Gatter
• 
  Ein XNOR-Gatter in CMOS unter Verwendung von normalen und invertieren Eingängen aus einem 2-2-AND-OR-Invert-Gatter

Integrierte Schaltkreise

Der Baustein 4077 aus der 4000er Logikfamilie sowie der 74x7266 aus der 74er Reihe beinhalten vier XNOR-Gatter mit je zwei Eingängen.

Literatur

• Klaus Beuth: Digitaltechnik. 10. Auflage. Vogel, 1998, ISBN 3-8023-1755-6. 
• Manfred Seifart, Helmut Beikirch: Digitale Schaltungen. 5. Auflage. Technik, 1998, ISBN 3-341-01198-6. 
• Ulrich Tietze, Christoph Schenk: Halbleiter-Schaltungstechnik. 12. Auflage. Springer, 2002, ISBN 3-540-42849-6. 

Einzelnachweise

1. ↑ ^{a b} P. Fischer: Aussagenlogik und Gatter. Universität Heidelberg, abgerufen am 21. Januar 2024.