Wasserwelle

Bei Wasserwellen handelt es sich um Oberflächenwellen an der Grenzfläche zwischen Wasser und Luft oder um eine interne Welle an der Grenzfläche zwischen zwei unterschiedlich dichten Wasserschichten im isopyknischen (geschichteten) Ozean. Nach Walter Munk sind damit alle Wasserspiegelauslenkungen mit Periodendauern von Zehntelsekunden bis Stunden (Gezeitenwelle) gemeint.

Bei Wellenlängen kleiner als 4 mm bestimmt die Oberflächenspannung des Wassers die Eigenschaften der Kapillarwellen, bei denen auch die Zähigkeit des Wassers starke dissipative Effekte bewirkt. Bei Wellenlängen größer als 7 cm sind die Massenträgheit, die Erdanziehungskraft und die dadurch bedingten Druck- und Bewegungsänderungen bestimmend für die Eigenschaften der Schwerewelle.

Wellenentstehung

Ins Wasser geworfene Steine und Strömungshindernisse erzeugen Wellen, fahrende Schiffe begleitet eine Bugwelle. Seebeben können Tsunamis hervorrufen. Auf letztere sowie auf Gezeitenwellen soll an dieser Stelle kein weiterer Bezug genommen, sondern vorzugsweise sollen durch Wind erzeugte Oberflächenwellen des Meeres in Abhängigkeit von der Wassertiefe behandelt werden.

• Video: Wie entsteht eine Wasserwelle? (Quelle: TerraX)
• Video von Meereswellen, die auf Gestein treffen
• Video einer Welle, deutlich erkennbar der Wasserrückzug vor der Welle, Brechen der Welle und anschließendes Auslaufen am Strand

Wellenentstehung durch Wind

Der Mechanismus der Wellenentstehung durch Wind ist die Kelvin-Helmholtz-Instabilität. Im Entstehungsgebiet des Seegangs sind als Einflussgrößen zu unterscheiden:

• die Streichlänge (Fetch) F = Einwirkungsdistanz des Windes an der Wasseroberfläche,
• die Windgeschwindigkeit U und
• die Winddauer als sogenannte Ausreifzeit ${\displaystyle D_{\text{min}}}$ des Seegangs.

Ihr Zusammenwirken entscheidet über die Größe der Wellen und über ihre Gestalt. Je größer eine dieser Einflussgrößen, desto größer die Wellen. In Flachmeeren hat die Wassertiefe begrenzenden Einfluss.
Der entstehende Seegang ist charakterisiert durch:

• die Wellenhöhen,
• die Wellenlängen,
• die Periodendauern und
• die Wellenfortschrittsrichtung (bezogen auf die Nordrichtung).

In einem vorgegebenen Seegebiet kommen Wellen mit unterschiedlichen Bandbreiten von Höhen und Perioden vor. Für die Wellenvorhersage sind als charakteristische Angaben definiert:

• die signifikante Wellenhöhe ${\displaystyle H_{S}=H_{1/3}}$ und
• die signifikante Wellenperiode ${\displaystyle T_{S}=T_{1/3}}$.

Beide beziehen sich auf die über einen vorgegebenen Zeitraum beobachteten Wellen und stellen als statistische Größen jeweils Mittelwerte für das Drittel der höchsten Wellen des Kollektivs dar.

Struktur und Eigenschaften

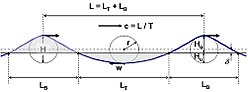
Wellenhöhe, Wellenlänge, Wellensteilheit

Wasserwellen weichen in ihrer Gestalt von der regelmäßigen Sinusform ab. Ihre Form ist sowohl horizontal als auch vertikal asymmetrisch. Der Teil der Welle, der oberhalb des Ruhewasserspiegels liegt, wird als Wellenberg bezeichnet. Die Position der höchsten Auslenkung ist der Wellenkamm. Der Teil der Welle, der unterhalb des Ruhewasserspiegels liegt, ist das Wellental. Die Wellenhöhe ist die Summe der Beträge beider benachbarter Maximalauslenkungen:

${\displaystyle H=H_{o}+H_{u}}$

Dabei übertrifft die maximale positive Wasserspiegelauslenkung in ihrem Betrage umso mehr die maximale negative Wasserspiegelauslenkung, je geringer die Wassertiefe wird. Bei Wellen im Flachwasserbereich kann die Höhe des Wellenberges bis zu 3/4 der gesamten Wellenhöhe ${\displaystyle H}$ ausmachen, während das Wellental ${\displaystyle H/4}$ unter dem Ruhewasserspiegel liegt. Als Wellenlänge (Symbol ${\displaystyle L}$) wird die Summe ihrer ungleichen auf den Ruhewasserspiegel bezogenen Teillängen des Kammbereiches und des Talbereiches bezeichnet, vergleiche Abbildung 1. Es gelten

${\displaystyle L_{B}<L_{T}}$

und

${\displaystyle L=L_{B}+L_{T}}$.

Der Quotient aus Wellenhöhe und Wellenlänge ist ein wichtiges Kennzeichen für die Beurteilung der Stabilität der Wellen und wird als Wellensteilheit S bezeichnet:

${\displaystyle S=H/L}$.

Nach Stokes (1847) gilt für Wellen über einer Wassertiefe ${\displaystyle d>L/2}$ der theoretische Grenzwert ${\displaystyle S_{\text{max}}=1/7}$. Tatsächlich erfolgt das Wellenbrechen aber bereits bei ${\displaystyle S=1/10}$. Auf dem freien Ozean herrschen Wellensteilheiten zwischen 1/100 und 1/50 vor. Für den Flachwasserbereich haben Naturmessungen die Formel von Miche (1944) bestätigt, in der auch die begrenzende Wirkung des Meeresbodens berücksichtigt ist:

Grenzsteilheit: ${\displaystyle \max \left({\frac {H}{L}}\right)=0{,}142\tanh {\left({\frac {2\pi d}{L}}\right)}}$

Seit dem 19. Jahrhundert ist die asymmetrische Form natürlicher Wasserwellen neben Gerstner (1804) vor allem von Stokes (1847) mit immer größerem mathematischen Aufwand beschrieben worden. Für praktische Abschätzungen wird dessen ungeachtet aber noch immer häufig die lineare Wellentheorie nach Airy-Laplace (1845) verwendet, die von der regelmäßigen Sinusform ausgeht.

Orbitalbewegung

Nach den Wellentheorien von Gerstner und Airy-Laplace werden über großer Wassertiefe die Wasserteilchen beim Passieren einer Welle näherungsweise auf Kreisbahnen (Orbitalbahnen) bewegt, deren Radien im Strömungsfeld unterhalb der Wasseroberfläche bis zu einer Tiefe, die etwa der halben Wellenlänge entspricht, nach einem Exponentialgesetz etwa auf null abnehmen. Dabei ist die Kreisperiode ${\displaystyle T=1/f}$ die Umlaufzeit, die dem Vorrücken der Welle um eine volle Wellenlänge ${\displaystyle L}$ entspricht. Somit ist die Orbitalgeschwindigkeit an der Wasseroberfläche

${\displaystyle w={\frac {2\pi r}{T}}}$,

und die Wellenfortschrittsgeschwindigkeit ${\displaystyle c_{w}}$ ist

${\displaystyle c_{w}={\frac {L}{T}}}$.

Demgegenüber sind die Bahnlinien der Wasserteilchen gemäß der Theorie von Stokes nach einer Wellenperiode nicht geschlossen. Nach dieser Theorie ist der zirkularen Orbitalbewegung eine horizontale Driftgeschwindigkeit U in Richtung der Wellenfortschrittsgeschwindigkeit c überlagert, die Massentransportgeschwindigkeit genannt wird. In der nebenstehenden Animation bezeichnen die roten Punkte die augenblicklichen Positionen der masselosen Teilchen, die sich mit der Strömungsgeschwindigkeit bewegen. Die hellblauen Linien sind die Bahnlinien dieser Teilchen und die hellblauen Punkte bezeichnen die Partikelpositionen nach jeder Wellenperiode. Die weißen Punkte sind gleichsinnig bewegte Flüssigkeitsteilchen. Man beachte, dass sich die Wellenperiode der Flüssigkeitsteilchen nahe der freien Oberfläche von derjenigen bezüglich einer festen Position (bezeichnet durch die hellblauen Punkte) unterscheidet. Dies ist auf den Dopplereffekt zurückzuführen.

Dispersion und Gruppengeschwindigkeit

(c) Mendax, CC BY-SA 3.0

(c) Mendax, CC BY-SA 3.0

Schwerewellen

Während die Wellenfortschrittsgeschwindigkeit (Phasengeschwindigkeit) ${\displaystyle c=L/T}$ für alle Wellenarten zutrifft, gilt für Schwerewellen zusätzlich die Dispersionsrelation, die neben der Wellenlänge ${\displaystyle L}$ auch die Wassertiefe ${\displaystyle d}$ als Variable enthält:

(1) ${\displaystyle c={\sqrt {{\frac {gL}{2\pi }}\tanh {\left({\frac {2\pi d}{L}}\right)}}}}$^[1]

${\displaystyle \pi }$: Kreiszahl

${\displaystyle g}$: Erdbeschleunigung

Die Abhängigkeit der Phasengeschwindigkeit von der Wellenlänge bzw. der Frequenz zeigen die beiden Abbildungen 2 und 3. Zusätzlich ist die Abhängigkeit von der Wassertiefe ${\displaystyle d}$ angegeben. Schwerewellen kommen nicht als einzelne monochromatische Wellen vor, sondern stets als Überlagerung von Wellen mit benachbarten Frequenzen. Als Folge treten Wellenpakete oder Wellengruppen auf, die sich mit der Gruppengeschwindigkeit

(2) ${\displaystyle c_{\text{g}}=c-L{\frac {\mathrm {d} c}{\mathrm {d} L}}}$

fortbewegen. Je nach Vorzeichen des Differentialquotienten ${\displaystyle {\tfrac {\mathrm {d} c}{\mathrm {d} L}}}$ ist die Gruppengeschwindigkeit kleiner, größer oder gleich der Phasengeschwindigkeit. Entsprechend unterscheidet man normale Dispersion, anomale Dispersion bzw. dispersionslose Wellenausbreitung. Bei Schwerewellen ist die Dispersion negativ, es liegt normale Dispersion vor (im Gegensatz zu Kapillarwellen).

Näherung: Die Wellenlängen sind klein relativ zur Wassertiefe (Tiefwasserwellen)

Für Gewässer mit einer Tiefe von mehr als einer halben Wellenlänge nähert sich ${\displaystyle \tanh(2\pi d/L)}$ in (1) dem Wert 1, die Phasengeschwindigkeit ${\displaystyle c}$ wird von der Wassertiefe unabhängig:

(3) ${\displaystyle c\approx {\sqrt {\frac {gL}{2\pi }}}}$ für ${\displaystyle L<2d}$

Bezeichnet ${\displaystyle T}$ die Periodendauer, folgt mit ${\displaystyle T={\frac {L}{c}}}$ aus (3):

(4) ${\displaystyle T\approx {\sqrt {\frac {2\pi L}{g}}}}$

Langwellige Wellen breiten sich also schneller aus und haben eine größere Periodendauer als kurzwellige. Bei einer Wellenlänge von 1 km ist c etwa 142 km/h und T etwa 25 s, bei einer Wellenlänge von 10 m ist c etwa 14 km/h und T etwa 2,5 s.

Die Dispersion wird maximal:

${\displaystyle {\frac {\mathrm {d} c}{\mathrm {d} L}}={\sqrt {\frac {g}{8\pi L}}}}$ bzw. ${\displaystyle {\frac {\mathrm {d} c}{\mathrm {d} f}}={\frac {-g}{2\pi f^{2}}}}$

Aus (2) ergibt sich die Gruppengeschwindigkeit ${\displaystyle c_{\text{g}}}$ zu

${\displaystyle c_{\text{g}}\approx {\frac {c}{2}}}$.

Aufgrund dieser Dispersionsrelation ändert sich die Zusammensetzung von Wellenpaketen in der Art, dass die längeren Wellen das Gebiet ihrer Erzeugung schneller verlassen als die kürzeren und somit an entfernten Orten früher ankommen. Da zusätzlich die kurzperiodischen Wellen stärker gedämpft werden, nimmt man Sturmwellen in entfernten Gebieten als langperiodische Dünung wahr.

Näherung: Die Wellenlängen sind groß relativ zur Wassertiefe

Bei Wellenlängen, die größer sind als die Wassertiefe (${\displaystyle L>20d}$), spricht man von Flachwasserwellen. Bei ihnen hängt die Ausbreitungsgeschwindigkeit nur von der Tiefe ${\displaystyle d}$ ab, nicht jedoch von der Wellenlänge. Für kleine ${\displaystyle x}$ gilt ${\displaystyle \tanh(x)\approx x}$ und damit erhält man aus (1)

(5) ${\displaystyle c\approx {\sqrt {gd}}}$ für ${\displaystyle d<{\frac {L}{20}}}$.

Bei tiefem Wasser können diese Wellen also sehr hohe Geschwindigkeiten erreichen. Das ist der Hintergrund dafür, dass sich Tsunamis im offenen Ozean sehr schnell ausbreiten. Gleichzeitig ist die Ausbreitungsgeschwindigkeit unabhängig von der Wellenlänge. Deshalb läuft ein Wellenpaket einer Flachwasserwelle bei der Ausbreitung kaum auseinander. Die Phasengeschwindigkeit ist genauso groß wie die Gruppengeschwindigkeit:

${\displaystyle {\frac {\mathrm {d} c}{\mathrm {d} L}}=0}$ bzw. ${\displaystyle {\frac {\mathrm {d} c}{\mathrm {d} f}}=0}$

${\displaystyle c=Lf={\sqrt {gd}}}$

${\displaystyle c_{\text{g}}=c}$.

Kapillarwellen

Bei Wellenlängen kürzer als einige Zentimeter bestimmt die Oberflächenspannung die Ausbreitungsgeschwindigkeit. Für Kapillarwellen gilt:

${\displaystyle c\,=\,L\,f\,=\,{\sqrt {\frac {2\pi \eta }{\rho L}}}\,=\,\left({\frac {2\pi \eta f}{\rho }}\right)^{1/3}}$

Darin bedeuten ${\displaystyle \eta }$ die Oberflächenspannung und ${\displaystyle \rho }$ die Dichte der Flüssigkeit. Die Dispersion von Kapillarwellen ist kleiner als Null und deshalb anomal:

${\displaystyle {\frac {\mathrm {d} c}{\mathrm {d} L}}={\frac {-\left(2\pi \eta L\right)^{-1/2}}{2L}}\quad }$bzw.${\displaystyle \quad {\frac {\mathrm {d} c}{\mathrm {d} f}}={\frac {2\pi \eta }{3\rho }}\,\left({\frac {2\pi \eta f}{\rho }}\right)^{-2/3}}$

Welleneffekte

Reflexion

Wellenreflexion bedeutet bei fortschreitenden Wasserwellen das Zurückwerfen eines Teils ihrer Energie (Wellenenergie) an einem Bauwerk (Wellenbrecher, Ufermauer, Uferböschung) oder an Orten, wo sich die Konfiguration des natürlichen Meeresgrundes (stark) ändert. Entsprechend dem Reflexionsgesetz der Optik wird zugleich ein anderer Anteil der Wellenenergie fortgeleitet und der restliche Anteil durch die Prozesse des Wellenbrechens, der Flüssigkeits- und Bodenreibung etc. dissipiert bzw. absorbiert, vergl. Wellentransformation, Wellenabsorption.

Refraktion

Unter Refraktion wird eine von der Wassertiefe abhängige Änderung der Wellenlaufrichtung bei Flachwasserwellen (Wellen mit Wellenlängen, die deutlich größer sind als die Wassertiefe) verstanden. Sie kommt durch eine von Ort zu Ort unterschiedliche Wellengeschwindigkeit zustande, die bei Flachwasserwellen von der Tiefe abhängt. Bei flach ansteigenden Stränden führt ihre Wirkung dazu, dass sich Wellenfronten zunehmend parallel zur Uferlinie einbeugen und der Beobachter am Strand die (nicht notwendigerweise brechenden) Wellen auf sich zukommen sieht. Wie bei der Brechung des Lichts ist auch hier das snelliussche Brechungsgesetz auf der Grundlage des huygensschen Prinzips anwendbar.

Diffraktion

Unter Diffraktion wird die Beugung von Wellenfronten an den Enden von Inseln bzw. an den Kanten von Bauwerken verstanden. Wie bei der Beugung des Lichtes an Kanten ist auch hier das huygenssche Prinzip anwendbar. Bei Schutzbauwerken (Wellenbrechern und Molen) hat die Diffraktion der Wellenfronten die Folge, dass ein Teil der Energie der anlaufenden Wellen auch hinter das Schutzbauwerk bzw. in den durch Molen gegen Wellenwirkungen zu schützenden Bereich einer Hafeneinfahrt gelangt.

Wellenbrechen

Wellenbrechen bezeichnet den kritischen Grad der Wellentransformation, bei dem die Oberflächenspannung am Wellenkamm überwunden wird, die Orbitalbewegung ihre charakteristische Form verliert und aus der Wellenkontur austretendes Wasser in den Vorderhang fällt. Hinsichtlich ihrer Geometrie können etwa vier Brecherformen unterschieden werden.

Beispiele für das Verhalten von Wellen beim Auflaufen auf einen Strand

Beispiel 1: Wellenbrechen

Nähert sich eine Welle einem langsam ansteigenden Ufer, verringert sich mit abnehmender Wassertiefe die Ausbreitungsgeschwindigkeit der Wellenfront. Die nachfolgenden Wellen überrollen die Wellenfront, bis auch sie abgebremst werden. Die Wellenlänge nimmt ab; als Folge der Energieerhaltung vergrößert sich die Wellenhöhe, bis das Wellenbrechen eintritt.

Beispiel 2: Refraktion

Nähert sich eine Wellenfront einem langsam ansteigenden Ufer im schrägen Winkel, verlangsamen sich die Wellen im flachen Bereich. Die weiter außerhalb liegenden behalten ihre Geschwindigkeit bei. Ähnlich wie bei der Brechung von Licht an Glas dreht sich dadurch die Wellenfront, bis sie parallel zur Strandlinie verläuft.

Grenzflächenwellen

Bei den Betrachtungen oben gehen nur die Parameter eines Mediums ein. Diese Annahme ist für Oberflächenwellen von Wasser an Luft gerechtfertigt, da der Einfluss der Luft aufgrund der kleinen Dichte vernachlässigbar ist.

Die erweiterte Fassung von Gleichung (3) berücksichtigt die Dichte beider Phasen, bezeichnet mit ${\displaystyle \rho _{1}}$ und ${\displaystyle \rho _{2}}$:

${\displaystyle c^{2}={\frac {\rho _{1}-\rho _{2}}{\rho _{1}+\rho _{2}}}\cdot {\frac {gL}{2\pi }}}$

Und bei Kapillarwellen gilt:

${\displaystyle c^{2}={\frac {2\pi \eta }{L(\rho _{1}+\rho _{2})}}}$

Besondere Wellen

Brandungswellen sind brechende Wellen in Strandnähe. Über die maximal mögliche Wellenhöhe H (vertikale Distanz zwischen Wellental und Wellenkamm) in Brandungszonen (= Brecherhöhe) entscheiden die Kriterien des Wellenbrechens. Naturmessungen haben gezeigt, dass Brecherhöhen sehr wohl größer werden können als die örtliche Wassertiefe.

Tsunamis werden durch Seebeben ausgelöst. Sie zeichnen sich aus durch eine sehr große Wellenlänge und auf hoher See durch kleine Amplituden von weniger als einem Meter. Die Ausbreitungsgeschwindigkeit von Tsunamis folgt der Beziehung (5), denn die Wellenlänge von mehreren 100 km ist deutlich größer als die Tiefe der Meere. Tsunamis breiten sich (bei einer mittleren Meerestiefe von 5 km) mit einer Geschwindigkeit von 800 km/h aus. In Küstennähe sinkt die Geschwindigkeit, während gleichzeitig die Höhe steigt. Verheerend sind die Schäden, die sie beim Auflaufen auf flache Küsten hervorrufen.

Gezeitenwellen sind Wellen, die durch die Tide verursacht werden.

An der Schichtung von leichtem Süßwasser auf schwerem Salzwasser beobachtet man Grenzflächenwellen, deren Auswirkungen auf Schiffe als Totwasser bezeichnet werden. Fährt ein Schiff in die Zone ein, kann es bei ausreichendem Tiefgang Bugwellen auf der Oberfläche der Salzwasserschicht erzeugen. Es verliert deutlich an Fahrt, ohne dass an der Wasseroberfläche Wasserwellen zu erkennen wären.

Als Grundsee wird eine kurze, steile und überbrechende Wasserwelle bezeichnet, deren Wellental bis auf den Grund reicht.

Einzelne, extrem hohe Monsterwellen können unter anderem durch Überlagerung entstehen. Starker Wind und eine gegenläufige Strömung begünstigen dies. Den oben beschriebenen Modellen zufolge ist allerdings die maximal mögliche Wellenhöhe begrenzt. Beim Entwurf von Schiffen ging man daher bis in die 1990er Jahre davon aus, dass Wellen mit einer Höhe von mehr als 15 m unmöglich oder zumindest extrem unwahrscheinlich seien. Dies wurde erstmals 1995 durch Messung widerlegt. Inzwischen belegen Satellitenbeobachtungen die Existenz von Monsterwellen mit Höhen von mehr als 30 m, die, im globalen Maßstab betrachtet, sogar relativ häufig (täglich) auftreten. Der Mechanismus ihrer Entstehung ist bis heute nicht vollständig verstanden und ist Gegenstand physikalischer Grundlagenforschung.^[2][3]

Weblinks

Wiktionary: Welle – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Wasserwelle – Sammlung von Bildern, Videos und Audiodateien

• Kinematik der Wasserwellenbewegung (PDF-Datei; 494 kB)
• Hella Kemper und Matthias Schütte: Da kommt 'ne Große! Meereswellen sind schön und gefährlich. Eine kleine Wellenkunde zum Welttag der Ozeane am 8. Juni. Die-Zeit-Infografik Nr. 623, Zeit Nr. 23, 2. Juni 2021, S. 46
• Ente auf Wasserwelle – Animation zur Veranschaulichung der Entstehung einer Wasserwelle

Literatur

• Pohl, Einführung in die Physik
• Fredric Raichlen: Waves. MIT Press Essential Knowledge Series, Cambridge, Mass. 2012, ISBN 0-262-51823-6.
• Franz Graf von Larisch-Moennich, Sturmsee und Brandung, Verlag von Velhagen und Klasing, 1925
• Petra Demmler: Das Meer – Wasser, Eis und Klima Verlag Eugen Ulmer, 2011. ISBN 3-8001-5864-7, Entstehung von Windsee, Dünung, Freak Waves, Gezeitenwellen, Sturmfluten und Tsunamis; populärwissenschaftliche Darstellung

Einzelnachweise

1. ↑ Andreas Mielke: Seminar: Theoretische Mechanik. Archiviert vom Original (nicht mehr online verfügbar) am 3. Januar 2017; abgerufen am 3. Januar 2017. 
2. ↑ future\u002Fauthor\u002Flucy-sherriff: Earth. In: bbc.com. Ehemals im Original (nicht mehr online verfügbar); abgerufen am 4. Februar 2024 (englisch).@1@2Vorlage:Toter Link/www.bbc.com (Seite nicht mehr abrufbar. Suche in Webarchiven) 
3. ↑ Zoe Heron: Freak Wave. BBC Horizon, - 2002 imdb