Wasserstoffbrennen

Mit Wasserstoffbrennen wird die Kernfusion von Protonen (d. h. von Atomkernen des häufigsten Isotops ¹H des Wasserstoffs) zu Helium im Inneren von Sternen (oder, im Fall einer Nova, auf der Oberfläche eines weißen Zwergs) bezeichnet, also mit anderen Worten die stellare Wasserstofffusion. Diese Reaktion stellt in normalen Sternen während des Großteils ihres Lebenszyklus die wesentliche Energiequelle dar. Alle Sterne der Hauptreihe beziehen ihre Energie aus dem Wasserstoffbrennen. Trotz der Bezeichnung handelt es sich nicht um eine Verbrennung im Sinne der chemischen Redoxreaktion, eine solche setzt um Größenordnungen weniger Energie frei.

Das Wasserstoffbrennen verläuft in mehreren Schritten entlang verschiedener Reaktionsketten. Die Energie- und Teilchenbilanz all dieser Prozesse ist jedoch dieselbe:

${\displaystyle \mathrm {4{}_{1}^{1}H\longrightarrow {}_{2}^{4}He+2e^{+}+2\nu _{e}+26{,}731\;MeV} }$.

Bei der Fusion von vier Protonen entstehen also neben dem Heliumkern zwei Positronen und zwei Elektron-Neutrinos. Alle anderen beteiligten Teilchen sind sowohl im Anfangs-, als auch im Endzustand vorhanden.^[1] Die frei werdende Energie von 26,731 MeV^[2] entspricht dem Massendefekt. Dieser Massendefekt ist der mit Abstand größte aller Fusionsreaktionen und somit bezüglich der Energie am ergiebigsten; die nächste Stufe stellarer Fusionsreaktionen, das Heliumbrennen, setzt pro erzeugtem Kohlenstoffkern nur noch etwa ein Viertel (7,3 MeV) davon frei.

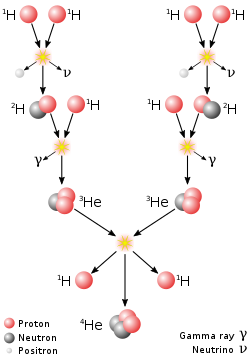
Die Fusion von Wasserstoff zu Helium kann nur in mehreren Schritten erfolgen. Kernfusion kann nur stattfinden, wenn zwei Kerne mit extrem hoher Energie aufeinanderprallen und sich auf wenige Femtometer nähern. Dass drei oder gar vier Protonen sich gleichzeitig derart annähern, ist so gut wie ausgeschlossen. Hinzu kommt, dass sich dabei Protonen in Neutronen umwandeln müssen, ein Prozess der schwachen Wechselwirkung, der sehr unwahrscheinlich ist.

Das Wasserstoffbrennen läuft daher vor allem in zwei verschiedenen Reaktionsketten ab:^[3]

• die Proton-Proton-Reaktion: Sie ist relativ direkt, erfordert aber im ersten Schritt der Kette beim Aufeinanderstreffen zweier Protonen die Umwandlung eines Proton in ein Neutron. Dies ist exorbitant unwahrscheinlich und der Grund, warum das Wasserstoffbrennen der Sonne Milliarden Jahre dauert,
• der Bethe-Weizsäcker-Zyklus (CNO-Zyklus): hier wirken die Elemente Kohlenstoff und Stickstoff als Katalysatoren. Protonen fusionieren mit diesen, der jeweils entstehende Kern ist β⁺-radioaktiv.

Bei beiden Prozessen wird Energie in Form von Bewegungsenergie der Endprodukte und Gammastrahlung frei. Die entstehenden Positronen annihilieren mit Elektronen zu Gammastrahlung. Die entstehenden Elektron-Neutrinos hingegen können den Stern praktisch ungehindert verlassen, deren Energie geht verloren. Daher hängt die dem Stern zur Verfügung stehende Energie von der Reaktionskette ab.^[4]

Die Energieerzeugungsrate ist bei der Proton-Proton-Reaktion proportional zur vierten Potenz der Temperatur, beim Bethe-Weizsäcker-Zyklus zur 18. Potenz.^[5] Mithin bewirkt eine Erhöhung der Temperatur um 5 % eine Steigerung von 22 % bzw. 141 % bei der Energiefreisetzung. Beim Heliumbrennen (27. Potenz) und Kohlenstoffbrennen (30. Potenz) liegen diese Werte nochmals deutlich höher.

Während der Hauptreihenphase findet das Wasserstoffbrennen im Kern des Sternes bei Temperaturen zwischen 5 und 55 Megakelvin statt.^[2] Für die Sonne bedeutet das, dass bei einer Kerntemperatur von 15,6 MK^[2] in jeder Sekunde etwa 564 Millionen Tonnen Wasserstoff zu 560 Millionen Tonnen Helium „verschmolzen“ werden, der Massendefekt also 4 Millionen Tonnen beträgt. Wenn der Wasserstoffvorrat im Kern erschöpft ist, der Stern also die Hauptreihe verlässt, findet weiteres Wasserstoffbrennen in einer Schale um den Kern statt. Dabei werden Temperaturen zwischen 45 und 100 MK erreicht.^[2]

Von der Art der Reaktionskette (CNO-Zyklus oder p-p-Zyklus) hängt ab, ob der Stern im Zentrum eine Konvektionszone oder eben keine besitzt. Der Temperaturgradient in einem Stern hängt zwar nicht von der Art der Reaktion ab (nur von seiner Masse), aber die Fusionsraten von p-p-Zyklus und CNO-Zyklus hängen unterschiedlich stark von der Temperatur ab. Damit Konvektion stattfindet, muss entweder die Opazität (wie in der Hülle von kühlen Sternen oder bei Sternen mit weniger als 0,35 Sonnenmassen) hoch sein oder der Energiefluss. Bei Sternen unter 1,12 Sonnenmassen und solaren Häufigkeiten von C, N und O ist der p-p-Zyklus noch die bestimmende Fusionsreaktion, welche relativ wenig von der Temperatur abhängt. Die Fusionsrate ist im Zentrum des Kerns am höchsten und nimmt nach außen dem Temperaturgradienten entsprechend langsam ab, die freiwerdende Energie kann dabei noch radiativ (durch Strahlung) übertragen werden. Bei Sternen mit 1,3 Sonnenmassen und mehr ist wegen der höheren Kerntemperatur der CNO-Zyklus die bestimmende Reaktion, bei der die Fusionsgeschwindigkeit sehr viel stärker an die Temperatur gekoppelt ist. Infolgedessen ist die gesamte Energieproduktion fast punktförmig im Kern solcher Sterne konzentriert, der Energiefluss ist hoch und die Übertragung im Kern erfolgt nun konvektiv (durch Strömung). Je schwerer der Stern ist, umso dichter reicht die Konvektionszone bis unter die Oberfläche: Sterne ab ~60 Sonnenmassen sind (anfangs) fast voll konvektiv. Mit abnehmendem Wasserstoffgehalt im Kern muss die Temperatur ansteigen, was dazu führt, dass Sterne mit radiativen Kernen zwischen 1,3 und 1,12 Sonnenmassen früher oder später während ihrer Hauptreihenphase vom p-p-Zyklus in den CNO-Zyklus wechseln und einen konvektiven Kern bekommen.

Die Konvektion im Kern von Sternen mit CNO-Zyklus führt zur ständigen Durchmischung und letztendlich dazu, dass der Wasserstoff am Ende der Hauptreihenphase schlagartig versiegt, während bei Sternen mit p-p-Zyklus der Kern langsam von innen her „ausbrennt“ und ein langsamer Übergang ins Schalenbrennen stattfindet. Sterne mit CNO-Zyklus müssen dagegen beim Versiegen des Wasserstoffs im Kern insgesamt so weit kontrahieren, bis die den ehemaligen Kern umgebende Kugelschale soweit aufgeheizt ist, dass dort das Wasserstoffschalenbrennen einsetzen kann. Die Kontraktion des gesamten Sterns bis zum Einsetzen des Schalenbrennens führt nun zu einer Aufheizung der Oberfläche, im Hertzsprung-Russell-Diagramm zeigen die Evolutionslinien von Sternen mit CNO-Zyklus einen charakteristischen „blauen Haken“, bevor die Entwicklung zum Riesenstern beginnt.^[6]

• Bogdan Povh et al.: Teilchen und Kerne. 4. Auflage. Springer Verlag 1997, ISBN 3-540-61737-X, S. 317–318.

1. ↑ Bradley W. Carroll, Dale A. Ostlie: An introduction to modern astrophysics. 2nd ed., Pearson new International ed. Pearson, Harlow 2014, ISBN 978-1-292-02293-2, S. 399. 
2. ↑ ^{a b c d} Christian Iliadis: Nuclear Physics of Stars. 2. Auflage. Wiley-VCH, Weinheim 2015, ISBN 978-3-527-33648-7, S. 353 (englisch). 
3. ↑ John N. Bahcall, M. C. Gonzalez-Garcia, Carlos Peña-Garay: Does the Sun Shine by pp or CNO Fusion Reactions? In: Physical Review Letters. 90, 2003, doi:10.1103/PhysRevLett.90.131301.
4. ↑ Christian Iliadis: Nuclear Physics of Stars. 2. Auflage. Wiley-VCH, Weinheim 2015, ISBN 978-3-527-33648-7, S. 364 (englisch). 
5. ↑ Eric G. Adelberger et al.: Solar fusion cross sections. II. The pp chain and CNO cycles. In: Reviews of Modern Physics. Band 83, Nr. 1, 2011, S. 226, doi:10.1103/RevModPhys.83.195. 
6. ↑ O.R. Pols: Stellar Structure and Evolution. Hrsg.: Astronomical Institute Utrecht. Chapter 9.3.