Unterabtastung

Unter der Unterabtastung (englisch undersampling) wird in der Signalverarbeitung die Abtastung eines Signalverlaufes mit weniger als der doppelten Bandbreite verstanden. Unter bestimmten Voraussetzungen werden dabei nicht die Bedingungen des Nyquist-Shannon-Abtasttheorems verletzt. Die Unterabtastung kann in diesem Fall dazu dienen, ein hochfrequentes Signal wie bei der Funktion eines Mischers in einen Zwischenfrequenzbereich mit geringerer Frequenz zu versetzen. Sind die Voraussetzungen des Abtasttheorems nicht erfüllt, so tritt zufolge der Unterabtastung Aliasing und damit einhergehend Informationsverlust auf. Die Unterabtastung stellt das Gegenstück zur Überabtastung (oversampling) dar.

Funktionsweise

Die oberen 2 Diagramme zeigen Fourier-Transformationen von 2 verschiedenen Funktionen, die die gleichen Ergebnisse liefern, wenn sie mit einer bestimmten Rate abgetastet werden. Die Basisbandfunktion wird schneller abgetastet als ihre Nyquist-Frequenz, und die Bandpassfunktion wird unterabgetastet, wodurch sie effektiv in das Basisband umgewandelt wird. Die unteren Grafiken zeigen, wie identische Ergebnisse durch die Aliase des Abtastprozesses erzeugt werden.

Die Fourier-Transformationen reellwertiger Funktionen sind symmetrisch um die 0-Hz-Achse. Nach der Abtastung steht nur noch eine periodische Summation der Fourier-Transformation (zeitdiskrete Fourier-Transformation) zur Verfügung. Die einzelnen frequenzverschobenen Kopien der ursprünglichen Transformation werden Aliase genannt. Das Frequenzoffset zwischen benachbarten Aliasen ist die Abtastrate, die mit ${\displaystyle f_{s}}$ bezeichnet wird. Wenn sich die Aliase gegenseitig spektral ausschließen, können die ursprüngliche Transformation und die ursprüngliche kontinuierliche Funktion oder eine frequenzverschobene Version davon aus den Abtastwerten wiederhergestellt werden. Der erste und dritte Graph (siehe Abbildung rechts) stellen ein Basisbandspektrum dar, bevor und nachdem es mit einer Rate abgetastet wurde, die die Aliase vollständig trennt.

Der zweite Graph zeigt das Frequenzprofil einer Bandpassfunktion, die das Band ${\displaystyle (A,A+B)}$ (blau schattiert) und sein Spiegelbild (beige schattiert) belegt. Die Bedingung für eine verlustfreie Abtastrate ist, dass sich die Aliase beider Bänder nicht überlappen, wenn sie um alle ganzzahligen Vielfachen von ${\displaystyle f_{s}}$ verschoben werden. Der vierte Graph zeigt das spektrale Ergebnis der Abtastung mit der gleichen Rate wie die Basisbandfunktion. Die Rate wurde ausgewählt, indem die niedrigste Rate gefunden wurde, die ein ganzzahliger Teiler von A ist und auch das Basisband-Nyquist-Kriterium erfüllt: ${\displaystyle f_{s}>2\cdot B}$. Folglich wurde die Bandpassfunktion effektiv in das Basisband umgewandelt. Alle anderen Raten, die eine Überlappung vermeiden, werden durch diese allgemeineren Kriterien gegeben, wobei ${\displaystyle A}$ und ${\displaystyle A+B}$ durch ${\displaystyle f_{L}}$ bzw. ${\displaystyle f_{H}}$ ersetzt werden:

${\displaystyle {\frac {2\cdot f_{H}}{n}}\leq f_{s}\leq {\frac {2\cdot f_{L}}{n-1}}}$ für alle ganzen Zahlen mit ${\displaystyle 1\leq n\leq \left\lfloor {\frac {f_{H}}{f_{H}-f_{L}}}\right\rfloor }$

Das höchste ${\displaystyle n}$, für das die Bedingung erfüllt ist, führt zu den niedrigsten möglichen Abtastraten. Wichtige Signale dieser Art sind das Zwischenfrequenzsignal, das Hochfrequenzsignal und die einzelnen Kanäle einer Filterbank. Wenn ${\displaystyle n>1}$ ist, führen die Bedingungen zu dem, was manchmal als Unterabtastung, Bandpassabtastung oder Verwendung einer Abtastrate von weniger als der Nyquist-Frequenz ${\displaystyle 2\cdot f_{H}}$ bezeichnet wird.

Die normale Basisbandbedingung für die reversible Abtastung, dass ${\displaystyle X(f)=0}$ außerhalb des Intervalls ${\displaystyle \left(-{\tfrac {f_{s}}{2}},{\tfrac {f_{s}}{2}}\right)}$ ist, und die rekonstruktive Interpolationsfunktion oder Tiefpass-Impulsantwort ist ${\displaystyle \operatorname {sinc} (t/T)}$.

Um eine Unterabtastung auszugleichen, lautet die Bandpassbedingung, dass ${\displaystyle X(f)=0}$ außerhalb der Vereinigung offener positiver und negativer Frequenzbänder,

${\displaystyle \left(-{\frac {n}{2}}\cdot f_{\mathrm {s} },-{\frac {n-1}{2}}\cdot f_{\mathrm {s} }\right)\cup \left({\frac {n-1}{2}}\cdot f_{\mathrm {s} },{\frac {n}{2}}\cdot f_{\mathrm {s} }\right)}$

die die normale Basisbandbedingung im Fall ${\displaystyle n=1}$ einschließt (außer dass, wo die Intervalle bei der Frequenz 0 zusammenkommen, sie geschlossen werden können). Die entsprechende Interpolationsfunktion ist der Bandpass, der sich aus dieser Differenz der Tiefpass-Impulsantworten ergibt: Bei abgetasteten Zwischenfrequenzsignalen oder Hochfrequenzsignalen hingegen ist die Rekonstruktion meist nicht das Ziel. Vielmehr kann die Abtastfolge als gewöhnliche Abtastungen des Signals behandelt werden, das in die Nähe des Basisbands frequenzverschoben ist, und auf dieser Grundlage kann die digitale Demodulation fortschreiten, wobei die Spektrumsspiegelung erkannt wird, wenn ${\displaystyle n}$ gerade ist.^[1][2]

Ein Signal in Bandpasslage weist allgemein eine Bandbreite ${\displaystyle B}$ von Signalanteilen auf, die symmetrisch um die Mittenfrequenz ${\displaystyle f_{0}}$ angeordnet sind. Um die Bedingungen des Nyquist-Shannon-Abtasttheorems nicht zu verletzen, darf das Signal außerhalb der Bandbreite keine Frequenzanteile aufweisen. Dies kann unter anderem durch Bandpassfilter vor der Unterabtastung gewährleistet werden.

Mit der Abtastfrequenz ${\displaystyle f_{A}}$ verschieben alle Abtastfrequenzen

${\displaystyle f_{A}={\frac {f_{0}-f'_{0}}{r}},\qquad r\in \mathbb {Z} }$

die Mittenfrequenz ${\displaystyle f_{0}}$ des Bandpasssignals auf die wählbare Bildfrequenz ${\displaystyle f'_{0}}$ im Basisband. Der Wert ${\displaystyle r}$ stellt den Faktor der Unterabtastung dar, mit größer werdendem ${\displaystyle r}$ werden die Abtastfrequenzen und somit nutzbaren Basisbandbreiten immer kleiner.

Die Bildfrequenz ${\displaystyle f'_{0}}$ im Basisband wird üblicherweise bei symmetrischem Bandspektrum auf den Wert ${\displaystyle f'_{0}=0}$ festgelegt. Bei unsymmetrischen Bandspektren wird ${\displaystyle f'_{0}={\frac {f_{A}}{4}}}$ gewählt.

Unterabtastung bei symmetrischem Bandspektrum

Bei symmetrischen Bandspektrum, wie zum Beispiel der Amplitudenmodulation, steht die Information im Signal doppelt und symmetrisch um ${\displaystyle f_{0}}$ zur Verfügung. Typisch wird in diesem Fall ${\displaystyle f'_{0}=0}$ gewählt, womit die Frequenzen im abgetasteten Signal durch

${\displaystyle f_{A}={\frac {f_{0}}{r}},\qquad r\in \mathbb {Z} \setminus \{0\}}$

gegeben sind. Die redundante Bandhälfte wird dabei auf negative Frequenzen abgebildet, wodurch die Demodulation besonders einfach wird. Die minimale Abtastfrequenz muss größer als die Bandbreite ${\displaystyle B}$ sein, womit sich mit dieser Nebenbedingung dann der Faktor ${\displaystyle r}$ bestimmten lässt zu:

${\displaystyle r={\frac {f_{0}}{B}}}$

Damit entspricht die Unterabtastung bei dem symmetrischen Bandspektrum der Demodulation einer Amplitudenmodulation.

Unterabtastung bei asymmetrischem Bandspektrum

Im Allgemeinen wird das Signal jedoch nur in eine niedrigere Zwischenfrequenzlage zur weiteren Verarbeitung verschoben (Funktion eines Mischers). Zur Erfüllung der Bedingungen des Nyquist-Shannon-Abtasttheorems wird ${\displaystyle f'_{0}=f_{A}/4}$ gewählt, die Frequenzen im abgetasteten Signal sind dann:

${\displaystyle f_{A}={\frac {4f_{0}}{4r+1}},\qquad r\in \mathbb {Z} }$

Die minimale Abtastfrequenz muss größer als die doppelte Bandbreite ${\displaystyle B}$ sein, womit sich mit dieser Nebenbedingung dann der Faktor ${\displaystyle r}$ bestimmten lässt zu:

${\displaystyle r={\frac {f_{0}}{2B}}-{\frac {1}{4}}}$

Nicht bandlimitierte Signale

(c) Moralapostel, CC BY-SA 3.0

Auswirkung der Samplingfrequenz im Verhältnis zur Signalfrequenz

Bei Unterabtastung nicht entsprechend bandlimitierter Signale sind die im Nyquist-Shannon-Abtasttheorem genannten Voraussetzungen zur verlustfreien Informationsgewinnung nicht erfüllt. Aliasing führt zum Auftreten von Spiegelfrequenzanteilen, die Teile des Nutzsignals überlagern.

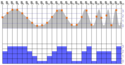
Die graue Schwingung sei das analoge Signal, das diskretisiert (z. B. digitalisiert) werden soll. Die blauen Zahlen rechts geben den Wertebereich an. Ein Sample, das in diesen Bereich fällt, erhält diese digitale Zahl zugeordnet (Quantisierung). Die senkrechten Linien (S₁ bis S₂₅) geben die Zeitpunkte an, zu denen abgetastet wird. Die roten × verdeutlichen, in welchen Wertebereich das jeweilige Sample fällt. Die rechteckige blaue Signalform repräsentiert das aus den digitalen Daten gewonnene Signal. (Ehe es einem Rekonstruktionsfilter zugeführt wird.)

In der Abbildung ist zu erkennen, dass ab Sample 20 (S₂₀) die digitalisierten Werte die abgetastete Frequenz nicht mehr repräsentieren. Das Signal wird daher mit einer deutlich geringeren Frequenz und damit fehlerhaft rekonstruiert.

Literatur

• Fernando Puente León, Uwe Kiencke, Holger Jäkel: Signale und Systeme. 5. Auflage. Oldenbourg, 2011, ISBN 978-3-486-59748-6. 

Einzelnachweise

1. ↑ Walt Kester: Mixed-signal and DSP design techniques
2. ↑ Hiroshi Harada, Ramjee Prasad: Simulation and Software Radio for Mobile Communications