Termlogik

Termlogik, in der Philosophie auch traditionelle Logik oder Begriffslogik genannt, bezeichnet diejenige Logik, die mit Aristoteles begann und die bis ins späte 19. Jahrhundert, als die moderne Prädikatenlogik entstand, dominierend war.

Um philosophische Texte, die vor der Entstehung der Prädikatenlogik entstanden sind (z. B. die mittelalterliche oder Leibniz’ und Kants Logik), zu verstehen, sind Grundkenntnisse der Terminologie und der Ideen der Termlogik unverzichtbar.

Aristoteles’ System

Aristoteles’ Werk ist in den sechs Texten zusammengefasst, die man insgesamt als Organon bezeichnet. Insbesondere zwei von diesen Texten, nämlich die Analytica priora und De Interpretatione enthalten das Kernstück seiner Logik, die Untersuchung von Urteilen und Schlussfolgerungen.

Die Grundlagen

Die Grundannahme der Theorie ist, dass Urteile (auch Aussagen oder Sätze; engl. propositions) aus zwei Termen zusammengesetzt sind – daher der Name Termlogik –, und dass der Vorgang der Schlussfolgerung auf Urteilen aufgebaut ist:

• Der Term ist derjenige Teil einer Rede, der etwas für sich bedeutet, wie Mensch oder sterblich, der aber nichts bedeutet, was wahr oder falsch sein kann.
• Das Urteil (griechisch apophansis): eine Verbindung von zwei Termen, die etwas anzeigt oder kundgibt, das wahr oder falsch sein kann.^[1] Das Urteil enthält zwei Terme, von denen der eine Term, das Prädikat, von einem anderen Term, dem Subjekt, bejahend oder verneinend ausgesagt wird.
• Der Syllogismus ist eine Schlussfolgerung, in der ein Urteil (die Konklusion) notwendig aus zwei anderen (den Prämissen) folgt.

Der Term

Der Term (griechisch horos, lateinisch terminus) ist die Grundkomponente des Urteils. Die Originalbedeutung von horos und auch von terminus ist Umgrenzung (lat. determinatio). Terme bedeuten Begriffe und umgrenzen Bedeutungen. Die beiden Terme liegen am Rande des Urteils, verbunden durch den Akt der Bejahung oder Verneinung.

Für Aristoteles ist ein Term einfach ein Ding, ein Teil des Urteils. Für die Logiker der Frühmoderne wie Arnauld (dessen Logik von Port-Royal der bekannteste Logiktext seiner Zeit war), Leibniz und Kant^[2] stehen Terme für Begriffe, Ideen oder Konzepte.

Sowohl für das Verständnis der traditionellen Termlogik als auch für deren angemessene Übersetzung in moderne Formalismen ist die Tatsache von Bedeutung, dass Subjekt und Prädikat in den klassischen Interpretationen gleichberechtigt sind und innerhalb unterschiedlicher Urteile auch die Plätze wechseln können: Der Terminus Mensch kann sowohl als Subjekt vorkommen (wenn ihm z. B. das Prädikat weiß zugesprochen wird) als auch als Prädikat (wenn z. B. dem Begriff Grieche das Prädikat Mensch zugesprochen oder dem Begriff Pferd dieses Prädikat abgesprochen wird).

Das Urteil

In der Termlogik ist ein (kategorisches) Urteil (oder: ein Satz, eine Proposition) eine besondere Satzart, in der Subjektterm und Prädikatterm verknüpft werden, so dass – in einer dazugehörenden Interpretation – etwas Wahres oder Falsches ausgesagt wird. Es gibt vier verschiedene Typen von Urteilen, nämlich das A-, I-, E- und O-Urteil, und diese Urteilsarten werden gemäß ihrer Qualität und ihrer Quantität klassifiziert (vgl. Quantität und Qualität von Urteilen):

Die logische Qualität eines Urteils kann bejahend sein (wenn das Prädikat zustimmend vom Subjekt ausgesagt wird) oder negativ (wenn dem Subjekt das Prädikat abgesprochen wird).

Die Quantität eines Urteils besagt, ob es total (oder allgemein) ist (das Prädikat wird „dem Ganzen“, gr. katholou, des Subjekts zu- oder abgesprochen) oder partikulär (gr. meros; das Prädikat wird nur einem Teil des Subjekts zu- oder abgesprochen).

Mit Hilfe dieser Begriffe ergibt sich die folgende Klassifikation:

Wenn ${\displaystyle S,P}$ Terme sind, dann schreibt man die vier Urteile meist in der Gestalt ${\displaystyle SaP,SiP,SeP,SoP}$; es sind aber auch andere Schreibweisen üblich.

In Worten liest man diese Urteile wie folgt:

Diese Sprechweise ist aus folgendem Grund problematisch: Sie scheint als selbstverständlich anzunehmen, dass eine extensionale Interpretation vorausgesetzt wird (s. den Abschnitt Intensionale und extensionale Interpretation); das heißt eine Interpretation, in der S und P für Mengen von Individuen stehen. Nun kann man – wenn auch in der deutschen Sprache etwas ungewohnt – auch eine intensionale Sprechweise wählen (etwa: P kommt S zu; oder: der Begriff S enthält den Begriff P), aber auch das würde das Problem nicht beheben, dass die Syntax der Termlogik einer semantischen Festlegung überhaupt nicht bedarf, dass aber stets – wie immer man spricht – eine solche Festlegung auf eine Standardsemantik mitschwingt.

Der Schluss (Syllogismus)

Aristoteles hat eine ausgefeilte Theorie des logischen Schlusses aufgestellt, die auf einzelnen Schlussregeln, den Syllogismen, beruht (siehe die ausführliche Darstellung in Allgemeine Darstellung des Syllogismus).

Er geht dabei von vollkommenen Syllogismen aus:

In Formelschreibweise kann man diese Regeln wie folgt schreiben.:

1. Aus CaB und BaA folgt CaA.
2. Aus CaB und BeA folgt CeA.

Zu diesem System gehören auch noch Konversionen wie

1. Aus AeB folgt BeA.
2. Aus AiB folgt BiA.
3. Aus AaB folgt BiA.

Aristoteles hat die letztgenannte Regel (die als Subalternation bezeichnet wird) durch das folgende Beispiel illustriert:

Algebraische Termlogik

Im Zuge der Algebraisierung der Logik im 19. Jahrhundert entstand 1847 der erste mathematische Logikkalkül von George Boole als Formalisierung der aristotelischen Termlogik. Auch Kalküle seiner Nachfolger John Venn, Ernst Schröder und Charles Sanders Peirce standen in dieser Termlogik-Tradition. Die älteren Formalisierungsversuche der Termlogik von Leibniz um 1690 wurden bereits 1840 publiziert, beeinflussten aber erst die Term-Kalküle von Giuseppe Peano.^[5]

Termlogik und Prädikatenlogik

Die moderne Prädikatenlogik, 1879 begründet durch die Begriffsschrift von Gottlob Frege, enthält eine Interpretation der Termlogik, wie sie auch heute noch vielfach angegeben wird.

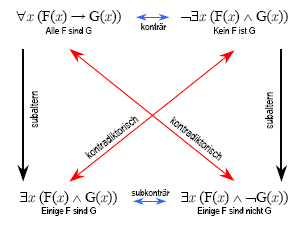
In seiner Begriffsschrift hat Frege das klassische Urteilsquadrat folgendermaßen skizziert (wir verwenden die heutige Schreibweise):

Diese fregesche Formalisierung, die von fast allen gängigen Lehrbüchern übernommen wurde, hat den Nachteil, dass sie wichtige Eigenschaften der Termlogik nicht wiedergibt. So ist beispielsweise die Subalternation (der Pfeil ganz links in der Skizze), in der Termlogik gemäß Aristoteles gültig:

nicht aber in der fregeschen „Übersetzung“ in die Prädikatenlogik:

Es ist versucht worden, dieses Problem durch Modifikationen der fregeschen Formeln zu beheben. So diskutiert Strawson^[6] mehrere Möglichkeiten; unter anderem die folgende:

Die fregesche Formulierung des Allurteils wird um eine Existenzannahme erweitert:

Die Idee dahinter ist die, dass bei „nichtleerer Subjektmenge“ die Subalternation gilt – was sicher richtig ist. Strawson stellt aber fest, dass diese Veränderung unerwünschte Folgen für das gesamte System hat – die Subalternation ist nun zwar gültig, aber andere, bisher richtige Gesetze stimmen nun nicht mehr. Seine Versuche, die fregesche prädikatenlogische Formulierung zu retten, erweisen sich als erfolglos.

Dass es überhaupt keine sinnvolle Formalisierung der Termlogik durch die (monadische) Prädikatenlogik erster Stufe gibt, hat der polnische Logiker Stanisław Jaśkowski bewiesen.^[7] Klaus Glashoff hat diese Ergebnisse durch einen computergestützten Beweis bestätigt.^[8]

Niedergang der Termlogik

Die Prädikatenlogik setzte sich im 20. Jahrhundert durch. Gleichzeitig geriet die Termlogik mit der dazugehörigen Syllogistik mehr und mehr außer Gebrauch; sie wurde fast nur noch im Bereich der Philosophie gepflegt. Die Termlogik überlebte auch im Rahmen der traditionellen Römisch-katholischen theologischen Ausbildung.^[9]

Moderne Termlogik

Die bedeutendste Entwicklung der Termlogik in neuerer Zeit ist John Corcorans Formalisierung der aristotelischen Logik durch natürliche Deduktion im Jahre 1973.^[10] Vorläufer ist Jan Łukasiewicz, der in seinem Buch^[11] die erste termlogische Formalisierung der aristotelischen Logik angab. Beide Systeme haben den Vorteil, dass sich die gesamte aristotelische Syllogistik ohne Zusatzannahmen, die bei Aristoteles nicht vorhanden sind (Existenzannahmen), herleiten lässt. Im Gegensatz zu Corcoran verwendet Łukasiewicz in seiner Formalisierung der aristotelischen Logik die Aussagenlogik, was seitdem häufig kritisiert wurde und durch Corcorans Arbeiten vermieden werden kann. Corcorans Theorie wird bei Philosophen und Logikhistorikern geschätzt, weil die Beweise durch Natürliches Schließen die Argumentation des Aristoteles in seiner Analytica priora fast wörtlich reproduzieren.^[12]

Im Folgenden werden die formalen Elemente der modernen, auf Corcoran zurückgehenden Termlogik beschrieben.

Kalkül der modernen Termlogik

Bausteine

Die Atome der Termlogik bestehen aus

1. den vier Zeichen A, I, E, O. Sie bezeichnen die klassischen vier Aristotelischen Urteilsformen;
2. den abzählbar vielen Termkonstanten (oder einfach Termen) ${\displaystyle a_{1},a_{2},a_{3},....}$. Man schreibt auch einfacher ${\displaystyle a=a_{1},b=a_{2},c=a_{3},...}$.

Die Variablen der Termlogik werden mit ${\displaystyle x_{1},x_{2},x_{3},...}$ bezeichnet, und man verwendet manchmal auch die Bezeichnung ${\displaystyle x=x_{1},y=x_{2},z=x_{3},...}$. Diese Variablen heißen auch als Termvariable.

Es gibt eine einzige Formationsregel; sie besagt, dass Zeichenketten der Form Aab, Iab, Eab, Oab zugelassen sind; hier können a und b beliebige Termkonstanten sein (also auch ${\displaystyle c,a_{5},a_{6},...}$ … usw. ).

Zeichenketten der Form Uab (wobei U eines der Atome A, I, E, O ist und a, b beliebige Terme sind ), werden als Urteile, Aristotelische Aussagen, oder kürzer nur als Aussagen bezeichnet. Sie sind die eigentlichen Bausteine der Termlogik.

Die Termlogik hat keine Axiome. Das bedeutet, dass die Regeln, die im folgenden Abschnitt behandelt werden, stets auf Annahmen angewendet werden. Insbesondere folgt daraus, dass es in dieser Logik keine Tautologien gibt.

Es existiert allerdings eine Variante der hier dargestellten Termlogik, bei der alle Ausdrücke der Gestalt Aaa Axiome sind.

Die folgende Sprechweise hat sich für die Urteile eingebürgert:

• Aab: Alle a sind b
• Iab: Einige a sind b
• Eab: Kein a ist b
• Oab: Nicht alle a sind b

In der Literatur findet man für die Urteile viele verschiedenen Darstellungen; so etwa – für unser Aab – auch aAb oder A(a,b).

Transformationsregeln

Die zum Kalkül der Termlogik gehörenden Transformationsregeln sind die folgenden:

• Beispiel: Aus den Annahmen ${\displaystyle {Aab,Ecb}}$ lassen sich mit Hilfe dieser Regeln z. B. die Folgerung ${\displaystyle Eac}$ ableiten, und zwar wie folgt:
• Aus ${\displaystyle Ecb}$ wird ${\displaystyle Ebc}$ abgeleitet nach R2
• Aus ${\displaystyle Aab,Ebc}$ wird ${\displaystyle Eac}$ abgeleitet nach R4

In diesem Fall schreibt man ${\displaystyle Aab,Ecb\vdash Eac}$.

Intensionale und extensionale Interpretation

Aristoteles hat in seiner Lehre vom Schluss^[13] in der Analytica priora bereits Terme allgemein bezeichnet, und zwar mit ${\displaystyle A,B,\Gamma ,M,N,\Theta }$ usw. Dies eröffnet die Möglichkeit, mit diesen Termkonstanten rein syntaktisch zu operieren, und es ist die Vorbedingung für eine kalkülmäßige Untersuchung seiner Termlogik.

Unabhängig von syntaktischen Fragestellungen, die bei den meisten Untersuchungen der Termlogik im Vordergrund stehen, wird seit langem über die Semantik der aristotelischen Termlogik diskutiert; d. h. über die Frage, was genau die Termkonstante bedeuten (oder: was sie bezeichnen, wofür sie stehen).^[14] Hier gibt es zwei unterschiedliche Möglichkeiten: die extensionale und die intensionale Semantik.

Die extensionale Semantik

In dieser Semantik geht man davon aus, dass die Termkonstanten für nichtleere Mengen (Ansammlungen von Individuen) stehen. Hiernach steht „Mensch“ für die Gesamtheit aller Menschen, und „Grieche“ steht für die Menge aller Griechen. Eine auf dieser Interpretation aufbauende Semantik bezeichnet man auch als Umfangslogik.

Die intensionale Semantik

Hierbei interpretiert man die Termkonstanten als Begriffe. Jeder Begriff hat andere, weitere Begriffe als Inhalt; z. B. hat der Begriff „Gold“ den Begriff „Metall“ als Inhalt. Dieses Beispiel stammt von Leibniz, der die beiden Möglichkeiten der Interpretation der Termlogik klar beschrieben hat.^[15]

Welche Semantik ist die historisch richtige?

Über die Frage, welche Interpretation – intensional oder extensional – Aristoteles bei seiner Analytica Priora im Sinne hatte, ist viel gestritten worden;^[16] Einzelne Autoren^[17] behaupten, dass die Lehre vom Unterschied von Extension und Intension schon bei Aristoteles zu finden sei und auch mittelalterliche Autoren bereits diesen Unterschied diskutiert hätten. Fest steht, dass diese Begriffe in der Logik von Port-Royal von Antoine Arnauld und dann später ausführlich und in einem ganz formalen Rahmen von Leibniz behandelt und einander als gleichwertig gegenübergestellt wurden, wobei Leibniz die intensionale Interpretation bevorzugte:

Kürzlich hat Klaus Glashoff, aufbauend auf den Arbeiten von Gottfried Wilhelm Leibniz, eine intensionale Semantik mit dem zugehörenden Vollständigkeitssatz angegeben.^[19]

Literatur

• Christoph Horn, Christof Rapp (Hrsg.): Wörterbuch der antiken Philosophie. Beck, München 2002, ISBN 3-406-47623-6, S. 501. 
• Otfried Höffe (Hrsg.): Aristoteles-Lexikon (= Kröners Taschenausgabe. Band 459). Kröner, Stuttgart 2005, ISBN 3-520-45901-9, S. XV, 640.
• Raili Kauppi: Über die Leibnizsche Logik mit besonderer Berücksichtigung des Problems der Intension und der Extension. In: Acta Philosophica Fennica. Fasc. XII, Helsinki 1960.
• Joseph Maria Bocheński: Ancient Formal Logic. North-Holland 1951.
• Louis Couturat: La Logique de Leibniz. Olms, Hildesheim 1961 (1901).
• Peter Geach: Reason and Argument. University of California Press, 1976.
• N.G.L. Hammond, H.H. Scullard (Hgg.): The Oxford Classical Dictionary. Oxford University Press, 1992, ISBN 0-19-869117-3.
• George Hayward Joyce: Principles of Logic. (Memento vom 27. Februar 2006 im Internet Archive) 3. Auflage. Longmans, 1949 (1908). (Ein Handbuch für den Gebrauch in Katholischen Seminaren. Referenzwerk zur traditionellen Logik, mit vielen Bezügen zu mittelalterlichen und antiken Quellen. Enthält keine Hinweise auf die moderne Logik. Der Autor lebte von 1864 bis 1943).
• Jan Łukasiewicz: Aristotle's Syllogistic, from the Standpoint of Modern Formal Logic. Oxford Univ. Press, 1951.
• John Stuart Mill: A System of Logic. 8. Auflage. London 1904.
• William Thomas Parry, Edward A. Hacker: Aristotelian Logic. State University of New York Press, 1991.
• Arthur Norman Prior: Formal Logic. Oxford University Press, 2. Auflage 1962.(Hauptsächlich über moderne formale Logik; der Text enthält aber einiges über Termlogik und mittelalterliche Logik).
• Arthur Norman Prior: The Doctrine of Propositions and Terms. Hrsg. Peter Geach, A. J. P. Kenny. Duckworth, London 1976.
• Willard Van Orman Quine: Philosophy of Logic. 2. Auflage. Harvard University Press, 1986.
• Lynn E. Rose: Aristotle's Syllogistic. Thomas, Springfield 1968.
• Fred Sommers: The Calculus of Terms. In: Mind 79. 1970, S. 1–39. Nachdruck in: G. Englebretsen (Hrsg.): The new syllogistic. Lang, New York 1987, ISBN 0-8204-0448-9.
• Fred Sommers: The logic of natural language. Oxford University Press, 1982.
• Fred Sommers: Predication in the Logic of Terms. In: Notre Dame Journal of Formal Logic. 31, 1990, S. 106–126.
• Fred Sommers, George Englebretsen: An invitation to formal reasoning. The logic of terms. Ashgate, Aldershot 2000, ISBN 0-7546-1366-6.

Weblinks

Wikibooks: Moderne Termlogik – Lern- und Lehrmaterialien

• Robin Smith: Aristotle's Logic. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
• Terence Parsons: Traditional Square of Opposition. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
• (Redaktion): Aristotle: Logik. In: J. Fieser, B. Dowden (Hrsg.): Internet Encyclopedia of Philosophy.
• Aristotelian Logic auf PlanetMath

Einzelnachweise

1. ↑ Die Römer übersetzten apophansis mit enuntiatio, propositio und iudicum. Aussage ist eine Übersetzung jüngsten Datums von enuntiatio. Iudicum kommt wesentlich bei Boethius vor und wurde von Leibniz als „Urteil“ ins Deutsche eingeführt und durch Wolff eingebürgert. Die Englische Logik spricht von jeher von proposition.
2. ↑ Immanuel Kant: Schriften zur Metaphysik und Logik. Werkausgabe Band VI. Hrsg. Wilhelm Weischedel. Suhrkamp, ISBN 3-518-27789-8, S. 521.
3. ↑ Lehre vom Schluss oder Erste Analytik. Erstes Buch, 4. Kapitel, S. 25.
4. ↑ Lehre vom Schluss oder Erste Analytik. Erstes Buch, 2. Kapitel, S. 25.
5. ↑ Peano, G: Logique mathématique. In: Peano: Formulaire de mathématique, Tome II, Turin 1897, S. 18 Zitatenliste, die meisten Zitate aus: G. W. Leibnitii Opera philophophica, ed. Erdmann, Berlin 1840.
6. ↑ P. F. Strawson: Introduction to Logical Theory. Methuen & Co., New York und London 1952. S. 125 ff.
7. ↑ Stanisław Jaśkowski: On the interpretations of Aristotelian categorical propositions in the predicate calculus. In: Studia Logica. 24 (1969), S. 161–172.
8. ↑ Klaus Glashoff: Zur Übersetzung der Aristotelischen Logik in die Prädikatenlogik.
9. ↑ Frederick Copleston: A History of Philosophy. Image Books 1993–1994, ISBN 0-385-46843-1.
10. ↑ John Corcoran: Completeness of an Ancient Logic. In: The Journal of Symbolic Logic. Band 37, Nr. 4, Dezember 1973.
11. ↑ Jan Łukasiewicz: Aristotle's syllogistic. From the standpoint of modern formal logic. Clarendon Press, Oxford 1951.
12. ↑ George Boger: Completion, Reduction and Analysis: Three Proof-theoretic Processes in Aristotle's Prior Analysis. In: History and Philosophy of Logic. 19, 1998, S. 187–226.
13. ↑ Aristoteles: Lehre vom Schluss oder Erste Analytik (Organon III). Meiner, Hamburg 1992, ISBN 3-7873-1092-4.
14. ↑ A. Hamacher-Hermes: Inhalts- oder Umfangslogik? Alber, Freiburg, München 1994, ISBN 3-495-47792-6.
15. ↑ Gottfried Wilhelm Leibniz: Sämtliche Schriften und Briefe. Reihe 6: Philosophische Schriften. Band 4, 1677–1690, Teil A, N. 1, N. 56 – N. 64 and N. 72. Akademie-Verlag, Berlin 1999.
16. ↑ Ellen Walther-Klaus: Inhalt und Umfang – Untersuchungen zur Geltung und zur Geschichte der Reziprozität von Extension und Intension. Hildesheim, Zürich, New York 1987.
17. ↑ z. B. Joseph C. Frisch: Extension and Comprehension in Logic. New York 1969.
18. ↑ Gottfried Wilhelm Leibniz: Sämtliche Schriften und Briefe. Reihe 6: Philosophische Schriften. Band 4, 1677–1690, Teil A, N.1, N. 56 – N. 64 and N. 72, Akademie-Verlag, Berlin 1999.
19. ↑ Klaus Glashoff: An intensional Leibniz Semantics for Aristotelian Logic. In: The Review of Symbolic Logic. 3, 2010, S. 262, doi:10.1017/S1755020309990396.