Stirling-Kreisprozess

Stirling-Kreisprozess im pV- und TS-Diagramm

Schema Stirlingmotor Vergleichsprozess

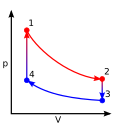
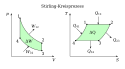
Der Stirling-Kreisprozess besteht aus je zwei isothermen und isochoren Zustandsänderungen und wird üblicherweise mit dem pV- und TS-Diagramm dargestellt. Der Stirling-Kreisprozess lässt sich beispielsweise durch eine Maschine mit zwei Kolben und einem Regenerator realisieren. Das nebenstehende Schema zeigt eine denkbare Anordnung. Die mit (1,2,3,4) gekennzeichneten Kolbenstellungen sind die Diagrammeckpunkte im pV- und im TS-Diagramm.

Der Stirlingmotor setzt diesen Kreisprozess näherungsweise um.

Funktionsweise

p-V-Diagramm des Stirling-Prozesses

Der Stirling-Kreisprozess besteht aus je zwei sich periodisch wiederholenden isothermen und isochoren Zustandsänderungen. Er dient als Vorlage für das Verständnis des Stirlingmotors, wird aber nur bei idealisierten Betrachtungen erreicht. Tatsächlich erreichen klassische Stirlingmotoren nicht einmal annähernd den im pV-Diagramm gezeigten idealisierten Prozess: Die Isothermen können technisch nicht implementiert werden, da sie nur ein Teilvolumen beeinflussen, nämlich das des beheizten / gekühlten Volumens. Das gesamte expandierte / komprimierte Volumen ist jedoch größer und betrifft die Gesamtgasmenge, die sich auch zum Teil in dem anderen Zylinder befindet. Die maximale Mischtemperatur über die gesamte Gasmenge ist niedriger, die minimale Mischtemperatur ist höher.

Der theoretische Prozess ist im nebenstehenden p-V-Diagramm dargestellt. Die rote Linie entspricht der Zustandsänderung des heißen Volumens, die blaue Linie die des kalten Volumens. Bei dem Kreisprozess wird das Arbeitsmedium periodisch expandiert und komprimiert. Die von der Maschine verrichtete Arbeit entspricht im p-V-Diagramm der Differenz der oberen und der unteren Isotherme, also der von den Linien umschlossenen Fläche.

Eine niedrige molare Masse des Arbeitsgases erhöht Effizienz und Leistung des Motors. Je größer der Arbeitsdruck ist, umso kompakter kann der Motor gebaut werden. Wasserstoff und Helium haben die höchste Wärmeleitfähigkeit, dadurch können die Wärmetauscher kompakt gestaltet werden. Wasserstoff hat zusätzlich den Vorteil der kleinsten Viskosität aller Gase, wodurch die geringsten Gasreibungsverluste auftreten. Wasserstoff hat etwa die 2,7-fache Wärmekapazität von Helium, das selbst eine 4,7-fache Wärmekapazität gegenüber Luft hat.

Für die Zustandsänderungen gilt unter Verwendung folgender Abkürzungen:

• ${\displaystyle Q,W}$ = Wärmemenge, Arbeit in J
• ${\displaystyle n}$ = Stoffmenge des Arbeitsgases in mol
• ${\displaystyle m}$ = Masse des Arbeitsgases in g
• ${\displaystyle M={\frac {m}{n}}}$ = Molmasse des Arbeitsgases in g/mol
• ${\displaystyle C_{V}}$ = Molare Wärmekapazität bei V=konst. in J mol⁻¹ K⁻¹
• ${\displaystyle R}$ = Universelle Gaskonstante in J mol⁻¹ K⁻¹
• ${\displaystyle T_{o},T_{u}}$ = obere, untere Prozesstemperatur in K
• ${\displaystyle V_{2},V_{3},V_{\text{UT}}}$ = Volumen im unteren Totpunkt in m³
• ${\displaystyle V_{1},V_{4},V_{\text{OT}}}$ = Volumen im oberen Totpunkt in m³

Im Weiteren sind die einzelnen Prozessschritte I bis IV erläutert.

pV-Diagramm

Diskontinuierlicher idealer Stirlingmotor

Isotherme Expansion

Prozessschritt I – Linie 1→2: Die isotherme Expansion von Volumen V₁ auf V₂ erfolgt mit konstanter Temperatur T_H, wobei die Wärme Q₁₂ aufgenommen und Arbeit W₁₂ abgegeben wird. Das Gasvolumen wird größer, der Druck sinkt, aber die Temperatur wird durch die Heizung konstant gehalten. Dabei verrichtet das Gas Arbeit durch Verschieben des Arbeitskolbens.

${\displaystyle Q_{12}=Q_{\text{zu}}=-W_{12}=n\cdot R\cdot T_{\text{H}}\cdot \ln {\frac {V_{2}}{V_{1}}}={\frac {m}{M}}\cdot R\cdot T_{\text{H}}\cdot \ln {\frac {V_{2}}{V_{1}}}}$

• n = Stoffmenge des Gases in mol
• m = Masse des Gases in g
• M = ${\displaystyle {\frac {m}{n}}}$ = Molmasse des Gases in g/mol
• C_v = Molare Wärmekapazität bei v=konst. in J mol⁻¹ K⁻¹
• R = Universelle Gaskonstante in J mol⁻¹ K⁻¹

Isochore Abkühlung

Prozessschritt II – Linie 2→3: Die isochore Abkühlung geschieht bei konstantem Volumen (V₂ = V₃) bei der die Wärme Q₂₃ vom Gas an den Regenerator abgegeben wird. Bei gleichbleibendem Volumen ändern sich Temperatur und Druck des Gases und der Regenerator speichert die Wärme. Das Verschieben der Kolben erfordert keine Arbeit, da auf beide der gleiche Druck wirkt.

${\displaystyle Q_{23}=\Delta E_{\text{Reg}}=n\cdot C_{\text{V}}\cdot (T_{\text{H}}-T_{\text{K}})}$

• ΔE_Reg = Änderung der thermischen Energie des Regenerators

Isotherme Kompression

Prozessschritt III – Linie 3→4: Die isotherme Kompression von Volumen V₃ auf V₄ erfolgt bei konstanter Temperatur T_K, wobei die Wärme Q₃₄ abgegeben und die Arbeit W₃₄ zugeführt wird. Das Gasvolumen wird kleiner, der Druck steigt aber die Temperatur wird durch die Kühlung konstant gehalten. Das Verschieben des Kolbens erfordert Arbeit.

${\displaystyle -Q_{34}=-Q_{\text{ab}}=W_{34}=n\cdot R\cdot T_{\text{K}}\cdot \ln {\frac {V_{3}}{V_{4}}}}$

Isochore Erwärmung

Prozessschritt IV – Linie 4→1: Die isochore Erwärmung geschieht bei konstantem Volumen (V₁ = V₄), bei der die Wärme Q₄₁ vom Gas aufgenommen und vom Regenerator abgegeben wird. Bei gleichbleibendem Volumen ändern sich Temperatur und Druck des Gases und der Regenerator gibt seine in Schritt II gespeicherte Wärme ab. Das Verschieben der Kolben erfordert keine Arbeit, da auf beide der gleiche Druck wirkt.

${\displaystyle Q_{41}=-\Delta E_{\text{Reg}}=n\cdot C_{\text{V}}\cdot (T_{\text{K}}-T_{\text{H}})}$

Die gesamte Prozessbeschreibung gilt für den unaufgeladenen Stirlingmotor. Der Druck hinter den Arbeitskolben ist also immer geringer als im Zylinder.

Nutzarbeit

Energiebilanz

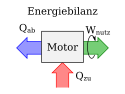
Die von der Maschine verrichtete Arbeit entspricht im oben dargestellten pV-Diagramm der vom Graphen umschlossenen Fläche. Im T-s-Diagramm wird die Arbeit in diesem Fall als Differenz der zugeführten und abgeführten Wärme dargestellt und ergibt die schraffierte Fläche. Die Nutzarbeit W_Nutzt lässt sich aus der Energiebilanz entsprechend der rechten Skizze ermitteln:

${\displaystyle Q_{\text{zu}}=Q_{\text{ab}}+W_{\text{Nutz}}}$

${\displaystyle W_{\text{Nutz}}=Q_{zu}-|Q_{ab}|}$

Mit obigen Beziehungen für Q_zu und Q_ab wird

${\displaystyle W_{\text{Nutz}}=n\cdot R\cdot T_{o}\cdot \ln \left({\frac {V_{2}}{V_{1}}}\right)-n\cdot R\cdot T_{u}\cdot \ln \left({\frac {V_{3}}{V_{4}}}\right)\ }$.

Setzt man für die Volumenverhältnisse

${\displaystyle {\frac {V_{2}}{V_{1}}}={\frac {V_{3}}{V_{4}}}={\frac {V_{UT}}{V_{OT}}}}$,

erhält man für die Nutzarbeit:

${\displaystyle W_{\text{Nutz}}=n\cdot R\cdot (T_{o}-T_{u})\cdot \ln \left({\frac {V_{UT}}{V_{OT}}}\right)}$

Wirkungsgrad

(c) Kino, CC BY-SA 3.0

Carnot-Wirkungsgrade für drei verschiedene Anfangstemperaturen

Der theoretische Wirkungsgrad des Stirlingmotors entspricht dem Carnot-Wirkungsgrad:

${\displaystyle \eta =1-{\frac {T_{u}}{T_{o}}}}$

Der tatsächlich realisierte Kreisprozess erreicht nicht das theoretische Maximum. Außerdem werden die Motoren selten auf eine obere Prozesstemperatur über 800 Kelvin (527 °C) ausgelegt, weil hochtemperaturfestes Material sehr teuer ist. Das Arbeitsgas im kalten Raum wiederum kann kaum unter 400 Kelvin (127 °C) gekühlt werden. Befeuerte Stirlingmotoren ohne Luftvorwärmung haben einen noch weit niedrigeren Wirkungsgrad, da der größere Teil der Wärmemenge vom Brennstoff nicht auf das Arbeitsgas übertragen werden kann. Mit einem Abgas-Wärmetauscher kann diese Wärme jedoch zur Vorwärmung der Verbrennungsluft genutzt und damit die Verluste verringert werden. Bei Niedertemperaturmaschinen, die zum Beispiel von nicht konzentrierter Sonnenstrahlung erhitzt werden, ist der Carnot-Wirkungsgrad entsprechend klein (mit T_o=53 °C und T_u=20 °C sind es 10 %). Die Verluste gegenüber der Carnot-Bedingung können jedoch gering gehalten werden.

Stirlingmotoren werden kommerziell zum Antrieb kleiner Elektrogeneratoren in Blockheizkraftwerken (BHKW) angeboten, da sie leiser sind als Verbrennungsmotoren. Stirlingmotoren in BHKW haben jedoch einen weit geringeren Wirkungsgrad als Verbrennungsmotoren. Das Verhältnis zwischen der Strom- (el.) und Wärmeproduktion (th.) beträgt nur ca. 1:6 oder 17 %,^[1] während Verbrennungsmotoren in BHKW 1:2,5 oder 40 % erreichen. Deshalb sind BHKW mit Stirlingmotor nur geeignet, wenn mit deren „schlechtem“ Wirkungsgrad hauptsächlich Raumwärme erzeugt werden soll oder wenn die Energiequelle extrem günstig ist.

Zusammenfassung

Warum kann der Stirlingmotor Arbeit abgeben? Man braucht ein Wärmegefälle. In der Expansionsphase muss ein Auskühlen des Gases verhindert werden und in der Kompressionsphase muss das Erhitzen des Gases unterdrückt werden. Der Wirkungsgrad entspricht dabei dem thermischen Wirkungsgrad.

${\displaystyle \eta ={T_{\text{H}}-T_{\text{K}} \over T_{\text{H}}}}$

• T_H = Heiß-Temperatur
• T_K = Kalt-Temperatur

In Prozessschritt I, der isothermen Expansion bei der hohen Temperatur T_H, nimmt das Gas im geschlossenen Zylinder Wärme auf und wandelt sie vollständig in Arbeit um. Der Druck p des Gases erzeugt auf die Fläche A des Arbeitskolbens eine Kraft F (= p*A). Bewegt sich dieser Kolben nun um den Weg Δs nach oben, so beträgt die dabei abgegebene Arbeit:

${\displaystyle |W|=F\cdot \Delta s=p\cdot A\cdot \Delta s=p\cdot \Delta V}$

Im pV-Diagramm des idealen Stirlingprozesses erkennt man anschaulich die verrichtete Arbeit als die Fläche unter der Linie 1→2, der Isothermen bei der Temperatur T_H, wieder.

Während Prozessschritt III, der isothermen Kompression bei niedriger Temperatur T_K, muss weniger Arbeit zugeführt werden, die Fläche unter der Linie 3→4, der Isothermen bei der Temperatur T_K, ist kleiner. Bei einer Umdrehung des Motors ist daher die vom Kreislauf umschlossene Fläche 1234 gerade die Arbeit W_ab, die insgesamt abgegeben wird.

${\displaystyle W_{\text{ab}}=W_{12}-W_{34}}$

Je größer die dargestellte Fläche 1234 ist, desto mehr Arbeit kann der Motor bei einer Umdrehung abgeben. Je größer das Verhältnis von W₁₂ zu W₃₄ umso besser der Wirkungsgrad.

Realer Stirlingprozess

Der ideale Stirlingprozess ist, wie auch alle anderen idealen Kreisprozesse, nicht genau zu realisieren. Das nachstehende pv-Diagramm zeigt mit der Fläche (gelb) die reale Leistung die zur Nutzung verbleibt im Vergleich zum vorstehenden idealen Prozess-Diagramm.

pV-Diagramm

Die folgende Auflistung der Gründe dafür ist gleichzeitig auch eine Einführung in die Problematik des Stirlingmotors.

Gründe für Wirkungsgradverluste

Einige Gründe, warum der reale Prozess vom idealen abweicht:

• mechanische Reibung
• Eine diskontinuierliche Kolbensteuerung ist nur begrenzt realisierbar

Um den Wirkungsgrad zu verbessern (der Prozess wird in den Ecken besser ausgefahren) und den Totraum so klein wie möglich zu halten, ist eine diskontinuierliche Kolbensteuerung sinnvoll. Der Nachteil ist höherer Verschleiß durch mechanische Belastung und die Geräuschentwicklung.

pV-Diagr. Auswirkung der Bewegungsart auf die Nutzarbeit (schraffierte Fläche)

• Durch hohe Gasgeschwindigkeit wird isotherme Zustandsänderung nur schlecht realisiert
• Regeneratorwirkungsgrad ist beschränkt
• Totraumeffekte

Im Idealfall befindet sich das gesamte Arbeitsmedium (Gas) im Expansions- und Kompressionsraum. Für noch bis 1999 realisierte Motoren beträgt der Totraum etwa 30 bis 50 % des Gesamtvolumens. Meistens befinden sich in diesen Toträumen (auch Schadräume genannt) die Wärmetauscheraggregate wie Erhitzer, Regeneratoren, Kühler. Dadurch geänderte Volumenverhältnisse bringen auch veränderte Druckverhältnisse mit sich, die sich sehr ungünstig auf den Gesamtwirkungsgrad auswirken.

• Wärmeverlust durch das Material

Dieser Wärmeverlust entsteht durch den Wärmestrom entlang des Zylinders nach außen in Richtung Temperaturgefälle.

• Dissipation durch Arbeitsgas- und Druckverlust

Dieser Verlust tritt bei Stirlingmaschinen mit einer Nenndrehzahl von mehr als 200/min verstärkt auf. Die Kompression und Expansion laufen dabei so schnell ab, dass der Wärmefluss, der für eine Isothermie nötig wäre, nicht mehr Schritt halten kann. Ergebnis ist der Druckanstieg bei der Kompression bzw. ein steiler Druckabfall bei der Expansion.

Weblinks

Commons: Stirling-Kreisprozess – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

1. ↑ senertec.de (Memento vom 11. August 2011 im Internet Archive)