Steinerbaumproblem

Das Steinerbaumproblem, ein nach dem Schweizer Mathematiker Jakob Steiner benanntes mathematisches Problem, ist eine Verallgemeinerung des Problems des minimalen Spannbaums. Hier wie dort wird der kürzeste Graph gesucht, der endlich viele gegebene Punkte (die Terminale) miteinander verbindet und der auf diese Weise das kürzeste Wegenetz zwischen diesen Punkten bildet. Beim Problem des minimalen Spannbaums wird dieser Graph nur zwischen den Terminalen aufgespannt, beim Steinerbaumproblem kann man dagegen aus einer ebenfalls gegebenen Menge (den Nichtterminalen) endlich viele weitere Punkte (die Steinerpunkte) zu den Ausgangspunkten hinzufügen, die dann als zusätzliche Verzweigungen im Wegenetz dienen, um dieses dadurch weiter zu verkürzen. Das Ergebnis ist wie beim minimalen Spannbaum ein Baum. Die theoretische und praktische Schwierigkeit beim Lösen des Steinerbaumproblems besteht darin, eine geeignete Auswahl der Steinerpunkte zu treffen.

Praktische Anwendung findet die Berechnung von Steinerbäumen unter anderem bei der Planung von Wege- und Telekommunikationsnetzen und dem Entwurf von integrierten Schaltkreisen^[1].

Beispiel

Minimaler Spannbaum (blau) und Steinerbaum (rot)

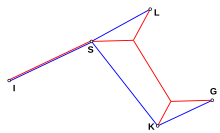
Die nebenstehende Zeichnung zeigt fünf Punkte, die die gegenseitige Lage der Flughäfen in Mittelösterreich darstellen. Stellt man sich die Aufgabe, alle diese Orte mit einem Netz minimaler Gesamtlänge von Fluglinien zu verbinden, so ergibt sich das blau eingezeichnete Netz, der minimale Spannbaum. Geht es aber um ein Autobahnnetz minimaler Länge, so kann man durch Anlage zweier Autobahndreiecke das Netz weiter verkleinern und es ergibt sich das rot eingezeichnete Netz, der Steinerbaum.

In diesem Beispiel sind die fünf Flughäfen die Terminale, alle anderen Punkte der Ebene die Nichtterminale und die beiden Autobahndreiecke die Steinerpunkte. Die Abstände sind die aus der euklidischen Geometrie. Solche Steinerbaumprobleme heißen daher „euklidisch“ oder auch „geometrisch“, weil die Lösung mit Hilfe geometrischer Eigenschaften der Steinerpunkte gefunden wird. Weiter unten gibt es ein Beispiel eines graphentheoretischen oder diskreten Steinerbaumproblems.

Definition

Im Folgenden werden zwei verschiedene mathematische Präzisierungen des Steinerbaumproblems gegeben. Sie sind nicht äquivalent; die Unterschiede werden im Anschluss diskutiert.

Voraussetzungen (allgemeine Variante): Gegeben sei eine Menge ${\displaystyle V}$, auf der eine Metrik definiert ist. Sei weiter ${\displaystyle T}$, die Menge der sogenannten Terminale, eine endliche Teilmenge von ${\displaystyle V}$.

Ist ${\displaystyle V}$ endlich, so bildet sie mit den Abständen einen kantengewichteten Graphen, und das Steinerbaumproblem lässt sich als rein graphentheoretisches Problem auffassen: Aus dem Graphen aller Punkte in ${\displaystyle V}$, der terminalen wie der nichtterminalen, wird dann ein Teilgraph bestimmt, der mindestens die Terminale enthält. Der letzte Absatz bekommt dann die folgende Gestalt:

Voraussetzungen (Graphen-Variante): Sei ${\displaystyle G=(V,E)}$ ein zusammenhängender, ungerichteter Graph ohne Mehrfachkanten, wobei ${\displaystyle V}$ die Knotenmenge und ${\displaystyle E}$ die Kantenmenge ist. Weiterhin sei ${\displaystyle T}$, die Menge der sogenannten Terminale, eine Teilmenge von ${\displaystyle V}$. Des Weiteren sei eine Funktion gegeben, die jeder Kante aus ${\displaystyle E}$ einen positiven reellen Wert, ihr Gewicht, zuordnet, ${\displaystyle G}$ ist also ein kantengewichteter Graph.

Problemstellung: Ausgehend von einer der beiden Voraussetzungen ist nun jeweils ein Graph gesucht, der alle Knoten aus ${\displaystyle T}$ verbindet und bei dem die Summe der Abstände bzw. Kantengewichte minimal ist. Dabei können, falls nötig, auch Knoten aus ${\displaystyle V\setminus T}$ verwendet werden; diese Knoten werden dann Steinerknoten oder Steinerpunkte genannt. Es ist leicht einzusehen, dass der Graph ein Baum ist. Dieser wird Steinerbaum genannt. Es kann für eine Aufgabenstellung mehrere minimale solche Bäume geben, also mehrere Steinerbäume, in manchen Metriken auch gar keine oder unendlich viele.

Normalerweise wird das Wort „Steinerbaum“ für einen solchen minimalen Baum gebraucht; der Ausdruck „minimaler Steinerbaum“ ist dann pleonastisch. Gelegentlich findet man aber auch „Steinerbaum“ als Bezeichnung für einen Baum, der von seiner Struktur als Lösung in Frage kommt, und man sucht die minimalen unter diesen. Der Begriff „Steinerbaum“ sollte also immer definiert werden, um Verwirrung zu vermeiden.

Die zweite Variante passt nur für endliche ${\displaystyle V}$. Die beiden Definitionen sind aber auch dann nicht ganz genau äquivalent:

• Der Graph ${\displaystyle G}$ in der Graphen-Variante wird in der Regel Paare von Knoten enthalten, zwischen denen es keine Kante gibt. Dem würde ein Abstand Unendlich in der Metrik entsprechen; eine Metrik ist aber immer reell. In der Praxis spielt das keine Rolle: man kann ja den nicht vorhandenen Kanten Gewichte zuordnen, die größer sind als die Summe aller Kantengewichte in ${\displaystyle G}$; solche Kanten können dann im Steinerbaum nicht vorkommen.
• Die Dreiecksungleichung wird in der Graphen-Variante nicht gefordert. Damit kann der Fall eintreten, dass eine direkte Kante durch einen Umweg über einen oder mehrere Steinerpunkte ersetzt werden muss, um den Graphen zu minimieren; insbesondere bei den in ${\displaystyle G}$ gar nicht vorhandenen Kanten ist das der Fall.

Diese nicht-metrischen Fälle von Kantengewichten im Graphen ${\displaystyle G}$ lassen sich aber auf den metrischen Fall zurückführen. Man bildet dazu einen vollständigen Graphen ${\displaystyle M}$ mit Kantengewichten, die eine Metrik bilden, und zwar ist in ${\displaystyle M}$ das Gewicht der Kante von ${\displaystyle A}$ nach ${\displaystyle B}$ als Länge (also Summe der Kantengewichte) eines kürzesten Pfades von ${\displaystyle A}$ nach ${\displaystyle B}$ in ${\displaystyle G}$ definiert. Dann löst man in ${\displaystyle M}$ das Steinerbaumproblem. Kommen im Steinerbaum dann Kanten vor, die in ${\displaystyle M}$ ein niedrigeres Kantengewicht haben als in ${\displaystyle G}$, so werden sie durch einen kürzesten Pfad in ${\displaystyle G}$ ersetzt; die Gesamtlänge des Steinerbaums ändert sich dadurch nicht und man bekommt eine Lösung des ursprünglichen nicht-metrischen Problems in ${\displaystyle G}$.

Euklidisches Steinerbaumproblem

Als Beispiel eines Steinerbaumproblems in einem metrischen Raum mit unendlich (sogar überabzählbar) vielen Punkten sei hier das euklidische Steinerbaumproblem genannt, also das Finden eines minimalen Wegenetzes zwischen endlich vielen Punkten in der Ebene. Das Beispiel am Anfang des Artikels ist euklidisch. Euklidische Steinerbaumprobleme sind die anschaulichsten und deswegen auch geschichtlich als erste erforschten. Der einfachste nichttriviale Fall, der Steinerbaum für drei Punkte in der Ebene, ist seit dem 17. Jahrhundert durch Torricelli gelöst^[2]: Falls jeder Winkel des gebildeten Dreiecks kleiner als 120° ist, ist der erste Fermat-Punkt des Dreiecks einziger Steinerpunkt und der Steinerbaum besteht aus den drei Verbindungslinien von dort zu den drei Ecken des Dreiecks (Beweis hier). Ist dagegen ein Winkel größer oder gleich 120°, so wird der Steinerbaum von dessen beiden Schenkeln gebildet. In beiden Fällen enthält der Steinerbaum des Dreiecks keinen Winkel kleiner als 120°. Daraus ergeben sich eine Reihe von Eigenschaften des Steinerbaums:

1. Nirgends im Steinerbaum kann ein Winkel zwischen Kanten auftreten, der kleiner als 120° ist, unabhängig davon, ob der Scheitel ein Terminal oder ein Steinerpunkt ist. Andernfalls könnte man die Schenkel des Winkels durch den Steinerbaum des vom Winkel gebildeten Dreiecks ersetzen und so den Steinerbaum durch einen kürzeren Graphen ersetzen.
2. Von den Steinerpunkten gehen immer genau drei Kanten aus, zwischen denen 120°-Winkel liegen. Einen Steinerpunkt zwischen weniger als drei Kanten könnte man weglassen, ohne den Steinerbaum zu verlängern, und bei mehr als drei Kanten würde Punkt 1 verletzt.
3. Sind alle ${\displaystyle n}$ Terminale Blätter des Steinerbaums (man nennt das einen vollen Steinerbaum), so gibt es genau ${\displaystyle n-2}$ Steinerpunkte, andernfalls weniger als ${\displaystyle n-2}$. Das ergibt sich unmittelbar aus Punkt 2.
4. Jeder Steinerbaum lässt sich eindeutig in kantendisjunkte volle Steinerbäume zerlegen; dabei gehören Terminale, die keine Blätter des Steinerbaums sind, zu so vielen Komponenten, wie von ihnen Kanten ausgehen, also zu zweien oder dreien.

Im Beispiel am Anfang des Artikels ist der Winkel bei ${\displaystyle S}$ größer als 120°, die anderen gleich 120°. Von den Steinerpunkten gehen jeweils drei Kanten aus. Der Punkt ${\displaystyle S}$ ist kein Blatt des Steinerbaums; deswegen hat der Steinerbaum weniger als 5–2=3 Steinerpunkte, nämlich nur 2. Der Steinerbaum lässt sich in die beiden vollen Steinerbäume mit den Terminalmengen ${\displaystyle \left\{I,S\right\}}$ und ${\displaystyle \left\{L,S,K,G\right\}}$ zerlegen.

Die genannten Eigenschaften von Steinerbäumen sind notwendig, aber nicht hinreichend. Weder ist ein Baum mit ${\displaystyle n}$ Blättern und ${\displaystyle n-2}$ inneren Punkten vom Grad 3 und Winkeln von 120° zwischen den Kanten notwendig von minimaler Länge, noch ist eine Vereinigung von Steinerbäumen notwendig minimal für die gesamte Terminalmenge, auch wenn die Bedingung 1 an der Nahtstelle eingehalten wird.

Die Konstruktion des Fermatpunktes lässt sich iterativ auch auf mehr als drei Punkte ausweiten. Allerdings führt sie im Allgemeinen zwar zu lokal minimalen Bäumen (d. h. der Baum wird bei keiner Verlagerung eines einzelnen Steinerpunkts kürzer), jedoch kommt man so nur dann zu einem globalen Minimum, wenn man alle der sehr zahlreichen Möglichkeiten durchprobieren würde, die sich bei jedem Schritt ergeben.

Graphentheoretisches Steinerbaumproblem

Beispiel

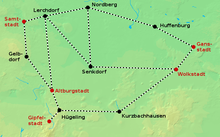
Karte des Schienennetzes des gedachten Staats. Großstädte sind rot eingezeichnet, Kleinstädte schwarz.

Ein Staat möchte sein marodes Schienennetz modernisieren, damit es mit Elektrolokomotiven befahren werden kann. Dafür sollen die vorhandenen Gleise mit Oberleitungen versehen werden; neue Gleise sollen nicht verlegt werden. Allerdings reicht das Budget nicht für eine Elektrifizierung des gesamten Netzes, weshalb sich die Regierung entschließt, nur so viele Strecken zu elektrifizieren, dass es möglich ist, von jeder Großstadt mit einer E-Lok in jede andere Großstadt zu fahren (dabei wird nicht ausgeschlossen, dass die E-Lok auch durch Kleinstädte fährt). Gleichzeitig sollen die Gesamtkosten für die Modernisierung möglichst gering gehalten werden. Vereinfachend wird in diesem Beispiel davon ausgegangen, dass die Kosten der Modernisierung nur von der Streckenlänge abhängen, nicht etwa von Geländebeschaffenheit usw.

Graphrepräsentation des Schienennetzes. Die Zahlen stehen für Streckenlängen in km. Der Steinerbaum ist rot markiert.

Graphentheoretisch kann man das Streckennetz als Graph betrachten, bei dem die Knoten Städte repräsentieren und die Kanten vorhandene Bahnstrecken zwischen den Städten. Jeder Kante wird ein Zahlenwert (ihr Gewicht) zugewiesen, der der Streckenlänge entspricht. Man kann nun die zu verbindenden Großstädte als Terminale auffassen. Die Aufgabe ist somit, eine gewichtsminimale Teilmenge der Kanten zu finden, die alle Terminale verbindet; sprich: ein Oberleitungsnetz zu finden, das alle Großstädte verbindet und dabei so kostengünstig wie möglich ist. Die Suche nach dieser Teilmenge entspricht der Suche nach einem Steinerbaum.

Der rechts abgebildete Steinerbaum repräsentiert all die Strecken, die elektrifiziert werden müssen, um alle Großstädte zu verbinden. Hierfür sind in diesem Beispiel 190 km Oberleitung nötig; mit weniger Leitung ist die Zielsetzung nicht zu erreichen.

Während es bei diesem Beispiel noch relativ leicht ist, den Steinerbaum zu finden, ist es für größere Schienennetze mit mehr Städten für Computer ebenso wie für Menschen praktisch unmöglich, eine optimale Lösung zu finden.

Komplexität des allgemeinen Problems

Die Entscheidungsvariante des graphentheoretischen Steinerbaumproblems ist wie folgt definiert. Man betrachtet natürliche Kantengewichte und eine natürliche Zahl k. Dann ist das Entscheidungsproblem, ob ein Steinerbaum mit Gewicht höchstens k existiert (Ja-Instanz). Die Entscheidungsvariante des graphentheoretischen Steinerbaumproblems gehört zur Liste der 21 klassischen NP-vollständigen Probleme, von denen Richard Karp 1972 die Zugehörigkeit zu dieser Klasse zeigen konnte. Damit ist das graphentheoretische Steinerbaumproblem NP-schwer. Nichtsdestotrotz ist es in der Praxis möglich, auch sehr große Steinerbaumprobleme mit teilweise Millionen von Kanten innerhalb kurzer Zeit optimal zu lösen.^[3][4] Da dies jedoch nicht theoretisch garantiert werden kann, sind in der Literatur viele Methoden untersucht worden, welche durch Approximierung eine vielleicht nicht optimale, aber dennoch „gute“ Lösung für ein gegebenes Steinerbaumproblem liefern.

Approximierbarkeit

Mit Hilfe eines Enumerationsalgorithmus ist die Berechnung eines minimalen Steinerbaumes in polynomieller Zeit möglich, falls die Zahl der Nicht-Terminale beschränkt ist, d. h. falls man sich auf Instanzen beschränkt, bei denen für ein vorgegebenes k nicht mehr als k Nicht-Terminale enthalten sind. Ein Spezialfall ist hier k=0, der mit der Suche nach einem minimalen Spannbaum identisch ist.

Der Dreyfus-Wagner-Algorithmus liefert einen minimalen Steinerbaum in polynomieller Zeit, falls die Zahl der Terminale logarithmisch in der Größe des Graphen beschränkt ist, d. h. falls man sich auf Instanzen beschränkt, bei denen für eine vorgegebene Konstante ${\displaystyle c}$ nicht mehr als ${\displaystyle c\cdot \log(|V|)}$ Terminale enthalten sind. Ein Spezialfall ist hier |T|=2, der mit der Suche nach einem kürzesten Pfad identisch ist.

Falls P ungleich NP ist (siehe P-NP-Problem), so gibt es auch keine polynomiellen Algorithmen, die beliebig gute approximative Lösungen liefern (PAS).^[5]

Die kombinatorischen Approximationsalgorithmen mit der besten bekannten Approximationsgüte sind der relative Greedy-Algorithmus (Approximationsgüte ${\displaystyle 1+\ln 2+\varepsilon <1{,}694}$) und der Loss-Kontraktions-Algorithmus (Approximationsgüte ${\displaystyle 1+\ln(3/2)+\varepsilon <1{,}550}$^[6]). Für beide Algorithmen wird vermutet, dass ihre Analyse bisher nicht bestmöglich ist. Insofern ist nicht klar, ob der relative Greedy-Algorithmus nicht doch besser als der Loss-Kontraktions-Algorithmus approximiert. Beide Algorithmen versuchen sogenannte k-Steinerbäume zu approximieren. Eine bessere Approximationsgüte von ${\displaystyle \ln(4)+\varepsilon <1{,}39}$^[7] erreicht ein LP-basierter Algorithmus. Bei allen genannten Algorithmen handelt es sich um Approximationsschemata, also eine Menge von Algorithmen, die die genannte Approximationsgüte für jedes beliebig kleine ${\displaystyle \varepsilon >0}$ erreichen. Ihre Laufzeit steigt allerdings sehr stark mit fallendem ${\displaystyle \varepsilon }$ und ist daher für reale Anwendungen unbrauchbar. Für die Beschränkung des Problems auf Distanzen 1 und 2 ist ein Polynomialzeit-Algorithmus mit Approximationsgüte 1,25 bekannt.^[8]

Effizientere Approximationsalgorithmen

Der Algorithmus von Kou, Markowsky und Berman erreicht Approximationsgüte 2 und ist mit Laufzeit O(|V|² · log|V| + |V| · |E|) wesentlich schneller als der relative Greedy-Algorithmus oder der Loss-Kontraktions-Algorithmus. Er berechnet dazu einen Distanzgraphen und darauf einen minimalen Spannbaum. Die Berechnung des Distanzgraphen bestimmt im Wesentlichen die Laufzeit des Algorithmus. Der Algorithmus von Mehlhorn verbessert diese Laufzeit auf O(|V| · log|V| + |E|), indem er statt eines vollständigen nur einen modifizierten Distanzgraphen berechnet.^[9] Auch der Algorithmus von Mehlhorn erreicht Approximationsgüte 2. Die Analyse der Algorithmen von Kou-Markowsky-Berman bzw. Mehlhorn ist bestmöglich.

Komplexität spezieller Varianten

Wie bei vielen anderen schweren Problemen der theoretischen Informatik gibt es auch für das Steinerbaumproblem zahlreiche einschränkende Varianten. Hierbei versucht man, durch Einschränkungen und Nebenbedingungen den Suchraum des Problems drastisch zu verkleinern und somit die Berechnung einer Lösung stark zu beschleunigen.

Das Steinerbaumproblem bleibt jedoch weiterhin NP-vollständig, wenn man sich auf bipartite ungewichtete Graphen beschränkt. Auch bei Beschränkung auf metrische Graphen bleibt das Problem noch NP-vollständig.

Oft wird das metrische Steinerbaumproblem auch so verallgemeinert, dass die Menge der Knoten unendlich ist, zum Beispiel wird bei vielen Problemstellungen die Ebene als Knotenmenge betrachtet. Die Knoten sind dann paarweise durch eine Kante entsprechend der verwendeten Metrik verbunden. Lediglich die Zahl der Terminale bleibt dann weiter endlich. Für euklidische Metriken oder die Manhattan-Metrik, die in praktischen Anwendungen relativ häufig gegeben sind, existieren polynomielle Approximationsschemata, so dass sich selbst für mehrere Tausend Knoten gute Lösungen des Problems finden lassen. Während sich das Steinerbaumproblem für die Manhattan-Metrik mit dem Hanangitter auf das Steinerbaumproblem in Graphen reduzieren lässt^[10], ist für das Steinerbaumproblem in der euklidischen Metrik nicht bekannt, ob es NP-vollständig ist, da die Zugehörigkeit zur Komplexitätsklasse NP unbekannt ist.

Siehe auch

• Chipentwurf
• Floorplanning

Einzelnachweise

1. ↑ Siehe z. B.: Chiang, C., Sarrafzadeh, M., Wong, C.K. Global routing based on Steiner min-max trees. In: IEEE Transactions on Computer-Aided Design. Vol. 9, No. 12, 1990. ISSN 0278-0070
2. ↑ Marcus Brazil, Ronald L. Graham, Doreen A. Thomas, Martin Zachariasen: On the history of the Euclidean Steiner tree problem. In: Archive for History of Exact Sciences. Band 68, Nr. 3, Mai 2014, ISSN 0003-9519, S. 327–354, doi:10.1007/s00407-013-0127-z (springer.com [abgerufen am 15. Oktober 2021]). 
3. ↑ Stefan Hougardy, Jannik Silvanus, Jens Vygen: Dijkstra meets Steiner: a fast exact goal-oriented Steiner tree algorithm. In: Mathematical Programming Computation. Band 9, Nr. 2, 1. Juni 2017, ISSN 1867-2957, S. 135–202, doi:10.1007/s12532-016-0110-1. 
4. ↑ Report by Polzin and Vahdati Daneshmand. Abgerufen am 11. Oktober 2021.
5. ↑ Clemens Gröpl, Stefan Hougardy, Till Nierhoff, Hans Jürgen Prömel. Lower Bounds for Approximation Algorithms for the Steiner Tree Problem. In: Lecture Notes in Computer Science. Bd. 2204/2001. Springer, ISSN 0302-9743, S. 217. (PS; 239 KB)
6. ↑ G. Robins, A. Zelikovsky. Improved Steiner tree approximation in graphs. In: Proceedings of the Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms. SODA 2000, 770-779 (PDF; 260 KB)
7. ↑ Michel X. Goemans, Neil Olver, Thomas Rothvoß, Rico Zenklusen: Matroids and Integrality Gaps for Hypergraphic Steiner Tree Relaxations. In: Proceedings of the 44th Symposium on Theory of Computing. STOC 2012, 1161-1176
8. ↑ Piotr Berman, Marek Karpinski, Alexander Zelikovsky (2009). "1.25-Approximation Algorithm for Steiner Tree Problem with Distances 1 and 2". Lecture Notes in Computer Science 5664: 86-97; doi:10.1007/978-3-642-03367-4_8
9. ↑ Kurt Mehlhorn. A Faster Approximation Algorithm for the Steiner Problem in Graphs. Information Processing Letters, 27(2):125-128, 1988.
10. ↑ M. Hanan, On Steiner’s problem with rectilinear distance, J. SIAM Appl. Math. 14 (1966), 255 - 265.

Literatur

• Hans Jürgen Prömel, Angelika Steger. The Steiner Tree Problem. A Tour through Graphs, Algorithms, and Complexity, Vieweg 2002, ISBN 3-528-06762-4.
• Marcus Brazil, Martin Zachariasen. Optimal Interconnection Trees in the Plane, Springer 2015, ISBN 978-3-319-13915-9.

Weblinks

• Ein Open Source Computerprogramm in C zur "exakten" Berechnung von minimalen euklidischen Steinerbäumen
• Ein Open Source Computerprogramm zur "exakten" Berechnung von minimalen graphentheoretischen Steinerbäumen
• Vorlesung zum Thema (auf Englisch) von Ronald L. Graham: The Shortest Network Problem (1988)