Sphärenbündel

Ein Torus ist ein Produkt zweier Kreise und damit ein Kreisbündel über dem Kreis

In der Mathematik sind Sphärenbündel Räume, die lokal wie ein Produktraum, dessen einer Faktor eine Sphäre ist, aussehen. Dazu gehören insbesondere Kreisbündel.

Definition

Ein Sphärenbündel ist ein Faserbündel, dessen Faser eine Sphäre ${\displaystyle S^{n}}$ ist.

Für ${\displaystyle n=1}$ spricht man von einem Kreisbündel.

Beispiele

• Das Einheits-Tangentialbündel einer differenzierbaren Mannigfaltigkeit ist ein Sphärenbündel.
• Eine Produkt-Mannigfaltigkeit ${\displaystyle M\times S^{n}}$ ist ein (triviales) Sphärenbündel.
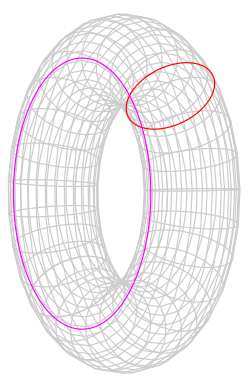
• Der Torus und die Kleinsche Flasche sind Kreisbündel über dem Kreis.
• Die Nichttrivialität eines Sphärenbündels wird durch seine Euler-Klasse gemessen, die wiederum in der Gysin-Sequenz Verwendung findet.

Literatur

• Raoul Bott, Loring Tu: Differential forms in algebraic topology. Graduate Texts in Mathematics 82. Springer-Verlag, New York-Berlin, 1982. ISBN 0-387-90613-4