Spektralsequenz

Eine Spektralsequenz^[1][2] oder Spektralfolge^[3] ist ein Grenzwertprozess zur Berechnung von Homologiegruppen im mathematischen Teilgebiet der homologischen Algebra. Nach J. F. Adams sind Spektralsequenzen wie exakte Sequenzen, nur komplizierter. Wie für exakte Sequenzen gelte auch für Spektralsequenzen: sie bieten keine Erfolgsgarantie, sind aber trotzdem in den Händen der Fachleute häufig ein effektives Werkzeug.^[4]

Die Grundidee geht auf eine 1946 von Leray veröffentlichte Forschungsankündigung zur kohomologischen Untersuchung einer Garbe zurück. Bereits 1947 hatte Koszul – mit Hilfe eines Hinweises von Cartan – das Spektralsequenz-Kalkül in der heutigen Form abstrahiert, so dass auch Leray in der vollständigen Version seiner Arbeit Koszuls Formalismus verwendete.^[5]

Formale Definition

Definition

Es sei ${\displaystyle {\mathcal {A}}}$ eine abelsche Kategorie, beispielsweise die Kategorie der Moduln über einem Ring, und es sei ${\displaystyle r_{0}}$ eine nicht-negative ganze Zahl. Eine kohomologische Spektralsequenz ist eine Sequenz ${\displaystyle \{E_{r},d_{r}\}_{r\geq r_{0}}}$ von Objekten ${\displaystyle E_{r}}$ mit Endomorphismen ${\displaystyle d_{r}:E_{r}\to E_{r}}$, sodass für jedes ${\displaystyle r\geq r_{0}}$ gilt:

1. ${\displaystyle d_{r}\circ d_{r}=0}$,
2. ${\displaystyle E_{r+1}\cong H_{*}(E_{r},d_{r}),}$ die Homologie von ${\displaystyle E_{r}}$ bezüglich ${\displaystyle d_{r}.}$

Die Isomorphismen werden oft weggelassen und man schreibt ${\displaystyle E_{r+1}=H_{*}(E_{r},d_{r}).}$ Ein Objekt ${\displaystyle E_{r}}$ wird auch als die r-te Seite oder der r-te Term bezeichnet, ein Endomorphismus ${\displaystyle d_{r}}$ wird Randoperator oder Differential genannt.

Bigraduierte Spektralsequenz

In der 'Realität' treten Spektralsequenzen meist in der Kategorie der bigraduierten Moduln über einem Ring R auf, das heißt jede Seite ist ein bigraduierter R-Modul ${\textstyle E_{r}=\bigoplus _{p,q\in \mathbb {Z} ^{2}}E_{r}^{p,q}.}$ In diesem Fall ist eine kohomologische Spektralsequenz also eine Sequenz ${\displaystyle \{E_{r},d_{r}\}_{r\geq r_{0}}}$ von bigraduierten R-Moduln ${\displaystyle \{E_{r}^{p,q}\}_{p,q}}$ und für jeden Modul die direkte Summe von Endomorphismen ${\displaystyle d_{r}=(d_{r}^{p,q}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1})_{p,q\in \mathbb {Z} ^{2}}}$ vom Bigrad ${\displaystyle (r,1-r)}$, sodass für jedes ${\displaystyle r\geq r_{0}}$ gilt:

1. ${\displaystyle d_{r}^{p+r,q-r+1}\circ d_{r}^{p,q}=0}$,
2. ${\displaystyle E_{r+1}\cong H_{*}(E_{r},d_{r})}$.

Die hier verwendete Notation heißt Komplementärgrad. Manche Autoren schreiben stattdessen ${\displaystyle E_{r}^{d,q}}$, wobei ${\displaystyle d=p+q}$ der totale Grad ist. In der nicht-graduierten Situation ist ${\displaystyle r_{0}}$ irrelevant, im bigraduierten Fall ist ${\displaystyle r_{0}}$ meist null, eins oder zwei.

Homologische Spektralsequenz

Meist sind die Objekte ${\displaystyle \{E_{r}\}_{r\geq r_{0}}}$ Kettenkomplexe, die mit aufsteigender (wie oben) oder absteigender Indizierung auftreten können. Im zweiten Fall erhält man, indem man ${\displaystyle E_{r}^{p,q}}$ durch ${\displaystyle E_{p,q}^{r}}$ und ${\displaystyle d_{r}^{p,q}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1}}$ durch ${\displaystyle d_{p,q}^{r}:E_{p,q}^{r}\to E_{p-r,q+r-1}^{r}}$ (Bigrad (-r,r-1)) ersetzt, analog die Definition einer homologische Spektralsequenz.

Spektralsequenz eines Kettenkomplexes

Das grundlegendste Beispiel (im nicht-graduierten Fall) ist die abelsche Kategorie der Kettenkomplexe. Ein Objekt ${\displaystyle (C_{\bullet },\,d)}$ hat ein natürliches Differential, den Randoperator ${\displaystyle d}$. Für ${\displaystyle r_{0}=0}$ ist die 0-te Seite ${\displaystyle E_{0}=C_{\bullet }}$ der Komplex selbst. Um das zweite Axiom der Definition zu erfüllen muss das nächste Objekt die Homologie des Kettenkomplexes sein, ${\displaystyle E_{1}\,=\,H(C_{\bullet })}$. Da das einzige natürliche Differential auf diesem Komplex die Nullabbildung ist, ist ${\displaystyle E_{2}}$ erneut die Homologie des Komplexes usw., das heißt ${\displaystyle E_{1}=E_{2}=E_{r}}$ für alle ${\displaystyle r\geq 1}$ und die Sequenz stabilisiert auf der ersten Seite. Um mehr Informationen aus einer Spektralsequenz zu bekommen, benötigen wir mehr Struktur auf den Objekten.

Visualisierung

Die Definition der Spektralsequenz ist sehr abstrakt, wir wollen die bigraduierte Situation visualisieren. Man kann sich das Objekt ${\textstyle E_{r}=\bigoplus _{p,q\in \mathbb {Z} ^{2}}E_{r}^{p,q}}$ als die r-te Seite eines karierten Buches vorstellen, an jedem Gitterpunkt ${\displaystyle (p,q)}$ ist ein Objekt ${\displaystyle E_{r}^{p,q}.}$ Zwischen einigen Objekten gibt es Verbindungslinien, die Differentiale. Auf die (r+1)-te Seite umzublättern bedeutet, Homologie zu bilden. Das heißt, die (r+1)-te Seite ist ein Subquotient der r-ten Seite. Die Differentiale ändern ihre Richtung bei jedem Umblättern.

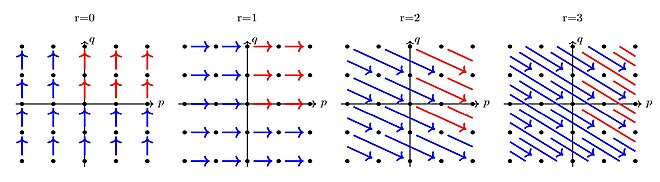
Die roten Pfeile demonstrieren eine sogenannte Erster-Quadrant-Spektralsequenz, bei der nur die Objekte im ersten Quadranten nicht-null sind. Der Bild- oder der Urbildbereich aller Differentiale wird mit wachsendem r zum Nullobjekt, siehe Beispiel unten.

Eigenschaften

Kategorische Eigenschaften

Die kohomologischen Spektralsequenzen bilden eine Kategorie. Ein Morphismus ${\displaystyle f:E\to E'}$ ist hierbei eine Familie ${\displaystyle \{f_{r}\}_{r\geq r_{0}}}$ von Abbildungen ${\displaystyle f_{r}:E_{r}\to E'_{r}}$, die mit den Differentialen und den Isomorphismen aus der Definition vertauschen: ${\displaystyle f_{r}\circ d_{r}=d'_{r}\circ f_{r}}$ und ${\displaystyle f_{r+1}(E_{r+1})\,=\,f_{r+1}(H(E_{r}))\,=\,H(f_{r}(E_{r}))}$. Im bigraduierten Fall sollen die Abbildungen außerdem die Graduierung respektieren: ${\displaystyle f_{r}(E_{r}^{p,q})\subset {E'_{r}}^{p,q}.}$

Multiplikative Struktur

Die Kohomologiegruppe wird mit dem Cup-Produkt zu einem Ring. Wir wollen daher auch auf der Spektralsequenz eine multiplikative Struktur definieren. Eine Spektralsequenz heißt multiplikativ oder Spektralring, falls gilt: (i) jede Seite ist eine bigraduierte Algebra, wobei die Differentiale Antiderivationen von Grad 1 sind, d. h. ${\textstyle d(a\cdot b)=(da)\cdot b+(-1)^{\deg(a)}a\cdot (db)}$ (ii) die Multiplikation auf ${\displaystyle E_{r+1}}$ ist durch diejenige auf ${\displaystyle E_{r}}$ induziert.

Konvergenz

Zykel und Ränder

Es sei eine Spektralsequenz ${\displaystyle \{E_{r}\}_{r\geq 1}}$ gegeben. Da sie aus Subquotienten besteht, induziert sie eine Sequenz von Subobjekten ${\displaystyle 0\,=\,B_{0}\,\supset \,B_{1}\,\supset \,B_{2}\,\supset \,...\,\supset \,Z_{2}\,\supset \,Z_{1}\,\supset \,Z_{0}\,=\,E_{1}}$ mit ${\displaystyle E_{r}=Z_{r}/B_{r}}$, gegeben durch die folgende induktive Relation: setze ${\displaystyle Z_{0}\colon =E_{1}}$, ${\displaystyle B_{0}\colon =0.}$ Sind ${\displaystyle Z_{r}}$ und ${\displaystyle B_{r}}$ schon definiert, dann seien ${\displaystyle Z_{r+1}}$ and ${\displaystyle B_{r+1}}$ die eindeutig bestimmten Objekte mit der Eigenschaft, dass ${\displaystyle Z_{r+1}/B_{r}=ker(d_{r}:E_{r}\to E_{r})}$ und ${\displaystyle B_{r+1}/B_{r}=im(d_{r}:E_{r}\to E_{r})}$. Wir setzen ${\displaystyle Z_{\infty }\colon =\cap _{r}Z_{r},}$ ${\displaystyle B_{\infty }\colon =\cup _{r}B_{r}}$ und definieren den Grenzterm der Spektralsequenz als ${\displaystyle E_{\infty }\colon =Z_{\infty }/B_{\infty }}$ (falls er in der betrachteten Kategorie definiert ist).

Konvergenz

Eine Spektralsequenz konvergiert schwach, falls es ein graduiertes Objekt ${\displaystyle H^{\bullet }}$ gibt mit einer Filtrierung ${\displaystyle F^{\bullet }H^{n}}$ für jedes ${\displaystyle n}$, und für jedes ${\displaystyle p}$ einen Isomorphismus ${\displaystyle E_{\infty }^{p,q}\cong F^{p}H^{p+q}/F^{p+1}H^{p+q}}$; in Symbolen:

${\displaystyle E_{r}^{p,q}\Longrightarrow H^{\bullet }}$.

Wir sagen, sie konvergiert gegen ${\displaystyle H^{\bullet }}$, falls die Filterung ${\displaystyle F^{\bullet }H^{n}}$ Hausdorff ist, das heißt ${\displaystyle \cap _{p}F^{p}H^{\bullet }=0}$. In der Praxis bezieht man sich auf den wichtigsten Term der Sequenz, welcher meist der erste oder der zweite ist, und schreibt ${\displaystyle E_{1}^{p,q}\Longrightarrow H^{\bullet }}$ oder ${\displaystyle E_{2}^{p,q}\Longrightarrow H^{\bullet }}$.

Weitere Konvergenzbegriffe

Im englischsprachigen Raum liest man die Wendung "a spectral sequence abuts", falls für jedes Tupel ${\displaystyle p,q}$ ein ${\displaystyle r(p,q)}$ existiert, sodass für alle ${\displaystyle r\geq r(p,q)}$ gilt ${\displaystyle E_{r}^{p,q}\,=\,E_{r(p,q)}^{p,q}}$. Die Seite ${\displaystyle E_{\infty }\,=\,E_{r(p,q)}}$ ist wieder der Grenzterm. Die Spektralsequenz ist regulär oder degeneriert bei ${\displaystyle \mathbf {r_{0}} }$, wenn ${\displaystyle d_{r}}$ verschwindet für alle ${\displaystyle r\geq r_{0}}$. Man sagt die Spektralsequenz kollabiert, falls insbesondere ein ${\displaystyle r_{0}\geq 2}$ existiert, sodass die ${\displaystyle r_{0}}$-te Seite auf eine Spalte oder eine Zeile konzentriert ist.

Allgemeine Konstruktionsmethoden

Es gibt viele Methoden, Spektralsequenzen zu konstruieren. Die folgenden sind die drei wichtigsten:

• Die Spektralsequenz eines exakten Paares^[6] (Konstruktion von William Massey);
• Die Spektralsequenz eines filtrierten Kettenkomplexes;
• Die Spektralsequenz eines Doppelkomplexes.

Der Doppelkomplex-Zugang ist lediglich ein besonders wichtiger Spezialfall des Filtrierten-Kettenkomplex-Zugangs, und jeder filtrierte Kettenkomplex induziert auf natürliche Weise ein exaktes Paar. Alle bekannten Spektralsequenzen können mithilfe der ersten Methode konstruiert werden.

Exaktes Paar

Wir beginnen wieder mit einer abelschen Kategorie, wie zuvor meist die Kategorie der bigraduierten Moduln über einem Ring. Ein exaktes Paar ist ein Paar von Objekten ${\displaystyle (A,E)}$, zusammen mit drei Homomorphismen ${\displaystyle i:A\to A}$, ${\displaystyle f:A\to E}$ und ${\displaystyle g:E\to A}$, welche die folgenden Exaktheit-Eigenschaften erfüllen:

• Bild ${\displaystyle i}$ = Kern ${\displaystyle f}$,
• Bild ${\displaystyle f}$ = Kern ${\displaystyle g}$,
• Bild ${\displaystyle g}$ = Kern ${\displaystyle i}$.

Man schreibt kurz ${\displaystyle (A,E,i,f,g)}$. ${\displaystyle E}$ wird der erste Term ${\displaystyle E_{0}}$ der Spektralsequenz sein. Für die zweite Seite bilden wir das abgeleitete Paar:

• ${\displaystyle d:=f\circ g}$
• ${\displaystyle A':=i(A)}$
• ${\displaystyle E':=Ker(d)/Im(d)}$
• ${\displaystyle i':=i|_{A'}}$
• ${\displaystyle g':E'\to A'}$ die induzierte Abbildung
• ${\displaystyle f':A'\to E'}$ ist folgendermaßen definiert: jedes ${\displaystyle a'\in A'}$ kann geschrieben werden als ${\displaystyle a'=i(a)}$ für ein ${\displaystyle a\in A}$. Setze ${\displaystyle f'(a')}$ als das Bild von ${\displaystyle f(a)}$ in ${\displaystyle E'}$.

Es kann leicht nachgerechnet werden, dass das abgeleitete Paar ${\displaystyle (A',E',i',f',g')}$ wiederum ein exaktes Paar ist^[7].

Setze also ${\displaystyle E_{r}:=E^{(r)}}$ und ${\displaystyle d_{r}:=f^{(r)}\circ g^{(r)}}$. Die Sequenz ${\displaystyle \{E_{r},d_{r}\}}$ ist eine Spektralsequenz.

Anwendung

• Serre-Spektralsequenz – (Ko-)Homologie einer Faserung
• Atiyah–Hirzebruch-Spektralsequenz – Kohomologie von außergewöhnlicher Kohomologietheorien, z. B. K-Theorie
• Bockstein-Spektralsequenz.
• Spektralsequenz eines filtrierten Kettenkomplexes

Filtrierter Kettenkomplex

Eine weitere wichtige Konstruktion ist die Spektralsequenz für einen filtrierten (Ko-)Kettenkomplex, da ein solcher auf natürliche Weise ein bigraduiertes Objekt induziert. Die Idee ist, die Kohomologie des filtrierten Komplexes mithilfe der Kohomologien der Objekte der Filtrierung zu berechnen.

Sei ${\displaystyle (C^{\bullet },d)}$ ein Kokettenkomplex, ${\displaystyle d}$ von Grad 1, mit einer absteigenden Filtrierung ${\textstyle ...\supset \,F^{-2}C^{\bullet }\,\supset \,F^{-1}C^{\bullet }\supset F^{0}C^{\bullet }\,\supset \,F^{1}C^{\bullet }\,\supset \,F^{2}C^{\bullet }\,\supset \,F^{3}C^{\bullet }\,\supset ...\,}$, wobei das Differential mit der Filtrierung kompatibel sei, d. h. ${\textstyle d(F^{p}C^{n})\subset F^{p}C^{n+1}}$, und zudem sei die Filtrierung erschöpfend und Hausdorff. Dann gibt es eine Spektralsequenz mit ${\textstyle E_{0}^{p,q}=F^{p}C^{p+q}/F^{p+1}C^{p+q}}$ und ${\textstyle E_{1}^{p,q}=H^{p+q}(F^{p}C^{\bullet }/F^{p+1}C^{\bullet })}$. Ist die Filtrierung auf ${\displaystyle C^{i}}$ zudem nach oben und unten beschränkt für jedes i, dann gilt ${\textstyle E_{\infty }^{p,q}=Gr^{p}(H^{p+q}(C^{\bullet }))}$ ^[8][9], d. h. die Spektralsequenz "abuts" (siehe Konvergenzbegriffe) gegen den p-ten graduierten Teil der ${\displaystyle (p+q)-}$ten Kohomologie.

Konstruktion

Um für die 0-te Seite der Spektralsequenz ein bigraduiertes Objekt zu konstruieren, betrachten wir das assoziierte graduierte Objekt:

${\displaystyle GrFC^{\bullet }=\bigoplus _{p\geq 0}Gr^{p}C^{\bullet }}$ mit ${\displaystyle Gr^{p}C^{\bullet }={\frac {F^{p}C^{\bullet }}{F^{p+1}C^{\bullet }}},}$

${\displaystyle E_{0}^{p,q}={\frac {F^{p}C^{p+q}}{F^{p+1}C^{p+q}}},}$

${\displaystyle E_{0}=\bigoplus _{p,q\in \mathbf {Z} }E_{0}^{p,q},}$

wobei ${\displaystyle d}$ ein natürliches bigraduiertes Differential ${\displaystyle d_{0}}$ auf ${\displaystyle E_{0}}$ induziert^[10]. Für die nächste Seite ${\displaystyle E_{1}}$ nehmen wir nun die Homologie von ${\displaystyle E_{0}}$ bezüglich ${\displaystyle d_{0}}$:

${\displaystyle E_{1}^{p,q}={\frac {\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}}{{\text{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}}}={\frac {\ker d_{0}^{p,q}:F^{p}C^{p+q}/F^{p+1}C^{p+q}\rightarrow F^{p}C^{p+q+1}/F^{p+1}C^{p+q+1}}{{\text{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}/F^{p+1}C^{p+q-1}\rightarrow F^{p}C^{p+q}/F^{p+1}C^{p+q}}},}$

${\displaystyle E_{1}=\bigoplus _{p,q\in \mathbf {Z} }E_{1}^{p,q}.}$

Die Filtrierung auf dem Kettenkomplex induziert eine Filtrierung auf der Homologie und wir können die assoziierte graduierte Kohomologie definieren:

$GrH(C^{\bullet })=\bigoplus _{p,q}Gr^{p}H^{q}(C^{\bullet })$ mit ${\displaystyle Gr^{p}H^{q}(C^{\bullet })=F^{p}H^{q}(C^{\bullet })/F^{p+1}H^{q}(C^{\bullet }).}$

Hat nun die Filtrierung nur Länge 1, dann ist ${\displaystyle E_{1}^{p,q}=H^{p+q}(F^{p}C^{\bullet })}$ (also die Homologie des assoziierten graduierten Objektes) isomorph zur assoziierten graduierten Kohomologie ${\displaystyle Gr^{p}(H^{p+q}(C^{\bullet }))=F^{p}H^{p+q}(C^{\bullet })/F^{p+1}H^{p+q}(C^{\bullet })}$^[11]. Im Allgemeinen machen wir dabei aber einen Fehler, da das Differential Elemente in der Filtrierung nach oben schiebt. Wir fahren daher mit der Approximation fort und definieren:

${\displaystyle Z_{r}^{p,q}=\{x\in F^{p}C^{p+q}|dx\in F^{p+r}C^{p+q+1}\},}$

${\displaystyle E_{r}^{p,q}={\frac {Z_{r}^{p,q}}{d(Z_{r-1}^{p-r+1,q+r-2})+Z_{r-1}^{p+1,q-1}}}.}$

Beachte, dass auch ${\displaystyle E_{0}^{p,q}}$ und ${\displaystyle E_{1}^{p,q}}$ auf diese Weise geschrieben werden können. Das Differential ${\displaystyle d_{r}}$ auf der r-ten Seite ${\displaystyle E_{r}}$ ist dabei jeweils durch das ursprüngliche Differential ${\displaystyle d}$ induziert. Es kann nun nachgerechnet werden, dass die entsprechende Homologie isomorph zu ${\displaystyle E_{r+1}}$ ist^[12], das heißt ${\displaystyle \{E_{r},d_{r}\}}$ ist eine Spektralsequenz.

Anwendung

• Konstruktion von gemischten Hodge Strukturen
• Hodge-de Rham-Spektralsequenz
• Spektralsequenz eines Doppelkomplexes

Doppelkomplex

Eine weitere Konstruktion ist die Spektralsequenz eines Doppelkomplexes ${\textstyle (C,d',d'')}$, bestehend aus einem bigraduierten Objekt ${\textstyle C=\bigoplus _{p,q\geq 0}C^{p,q}}$ mit zwei Differentialen ${\textstyle d':C^{p,q}\to C^{p+1,q}}$ und ${\textstyle d'':C^{p,q}\to C^{p,q+1}}$, also ${\textstyle d'^{2}=d''^{2}=0}$. Die Differentiale sollen zudem antikommutieren,, d. h. ${\textstyle d'd''+d''d'=0}$. Der assoziierte einfache Komplex ${\textstyle (Tot(C^{\bullet }),D)}$ ist definiert durch

${\displaystyle C^{i}=\bigoplus _{p+q=i}C^{p,q}}$ mit ${\displaystyle D=d'+d''}$

Wir wollen ${\textstyle H'^{i}(H''^{j}(C^{\bullet ,\bullet }))}$ und ${\textstyle H''^{j}(H'^{i}(C^{\bullet ,\bullet }))}$ vergleichen, indem wir nun zwei Filtrierungen betrachten:

${\displaystyle 'F^{i}C^{n}=\bigoplus _{p+q=n \atop p\geq i}C^{p,q}}$ und

${\displaystyle ''F^{j}C^{n}=\bigoplus _{p+q=n \atop q\geq j}C^{p,q}}$.

Dann existieren zwei Spektralsequenzen mit

${\displaystyle ('E_{2})^{p,q}=H'^{p}(H''^{q}(C^{\bullet ,\bullet }))}$ und

${\displaystyle (''E_{2})^{p,q}=H''^{q}(H'^{p}(C^{\bullet ,\bullet })),}$

wobei gilt ${\displaystyle 'E_{2}^{p,q}\Longrightarrow H(Tot(C^{\bullet }),D)}$ und ${\displaystyle ''E_{2}^{p,q}\Longrightarrow H(Tot(C^{\bullet }),D)}$^[13].

Beispiele

Erster-Quadrant-Spektralsequenz

Betrachten wir eine Spektralsequenz, bei der ${\textstyle E_{r}^{p,q}}$ verschwindet für alle ${\displaystyle p}$ kleiner als ein ${\displaystyle p_{0}}$ und für alle ${\displaystyle q}$ kleiner als ein ${\displaystyle q_{0}}$. Für ${\displaystyle p_{0},q_{0}=0}$ sprechen wir von einer Erster-Quadrant-Spektralsequenz. Bei dieser Sequenz gilt ${\textstyle E_{r+i}^{p,q}=E_{r}^{p,q}}$ für alle ${\displaystyle i\geq 0}$, wenn ${\displaystyle r>p}$ und ${\displaystyle r>q+1}$ (im Englischen würde man also sagen, 'the spectral sequence abuts', siehe Konvergenzbegriffe). Beachte hierfür, dass entweder das Bild oder das Urbild der Randoperatoren in den genannten Fällen null ist. Die Spektralsequenz muss allerdings nicht degenerieren, da nicht alle Differentiale gleichzeitig null sein müssen. Bildlich gesprochen stabilisiert sich die Spektralsequenz in einem wachsenden Viereck. Ähnlich funktionieren auch die Fälle für ${\displaystyle p_{0},q_{0}\geq 0}$.

Fünfterm exakte Sequenz

Sei ${\displaystyle \{E_{r}\}}$ eine bigraduierte Erster-Quadrant-Spektralsequenz. Dann ist die Sequenz

${\displaystyle 0\to E_{2}^{1,0}\to E^{1}\to E_{2}^{0,1}{\overset {d}{\to }}E_{2}^{2,0}\to E^{2}}$

exakt. Sie wird Fünfterm exakte Sequenz genannt.

Leray-Serre-Spektralsequenz

Sei ${\displaystyle F\rightarrow E\rightarrow B}$ eine Serre-Faserung mit einfach zusammenhängendem Basisraum ${\displaystyle B}$. Durch Weiterentwicklung von Lerays ursprünglichem Ansatz^[14] gewann Serre eine Spektralsequenz ${\displaystyle H_{p}(B;H_{q}(F))\Rightarrow H_{p+q}(E)}$.^[15] Serre benutzte seine Spektralsequenz, um die Homologie von Schleifenräumen zu studieren. Die Gysin-Sequenz folgt unmittelbar aus dieser Spektralsequenz.^[16]

Grothendieck-Spektralsequenz

Grothendieck entdeckte eine Spektralsequenz, die die abgeleiteten Funktoren einer Verknüpfung von zwei Funktoren berechnet. Seien ${\displaystyle F\colon {\mathcal {A}}\rightarrow {\mathcal {B}}}$ und ${\displaystyle G\colon {\mathcal {B}}\rightarrow {\mathcal {C}}}$ zwei linksexakte Funktoren zwischen abelschen Kategorien, wobei ${\displaystyle {\mathcal {A}}}$ und ${\displaystyle {\mathcal {B}}}$ genügend viele injektive Objekte haben. Es gelte außerdem: Ist ${\displaystyle I}$ ein injektives Objekt von ${\displaystyle {\mathcal {A}}}$, dann ist ${\displaystyle F(I)}$ ein ${\displaystyle G}$-azyklisches Objekt von ${\displaystyle {\mathcal {B}}}$. Dann gibt es eine Spektralfolge ${\displaystyle R^{p}G(R^{q}F(A))\Rightarrow R^{p+q}(G\circ F)(A)}$ für jedes Objekt ${\displaystyle A}$ von ${\displaystyle {\mathcal {A}}}$.^[17][18] Die entsprechende Aussage für linksabgeleitete Funktoren gilt ebenfalls.^[18][19]

Lyndon-Hochschild-Serre-Spektralsequenz

Diese Spektralsequenz in der Gruppenkohomologie wurde von 1953 von Hochschild und Serre entdeckt, nach Vorarbeiten von Lyndon. Sie kann als Anwendungsbeispiel der Grothendieck-Spektralsequenz hergeleitet werden. Sei ${\displaystyle G}$ eine Gruppe mit Normalteiler ${\displaystyle N}$, und sei ${\displaystyle M}$ ein ${\displaystyle \mathbb {Z} G}$-Modul. Dann gibt es eine Spektralfolge ${\displaystyle H^{p}(G/N;H^{q}(N;M))\Rightarrow H^{p+q}(G,M)}$.^[20][21]

Atiyah-Hirzebruch-Spektralsequenz

Sei ${\displaystyle h^{*}}$ eine verallgemeinerte Kohomologietheorie und ${\displaystyle X}$ ein CW-Komplex. Dann gibt es eine bedingt konvergierende Spektralsequenz ${\displaystyle H^{p}(X;h^{q}(*))\Rightarrow h^{p+q}(X)}$, wobei mit ${\displaystyle *}$ der topologischer Raum gemeint ist, der aus genau einem Punkt besteht.^[22][23] Atiyah und Hirzebruch verwendeten diese Spektralsequenz im Fall der verallgemeinerten Kohomologietheorie K-Theorie.^[24] Maunder benutzte Postnikow-Systeme, um eine Alternativkonstruktion der Atiyah-Hirzebruch-Spektralsequenz zu geben, die eine bessere Beschreibung der Differentiale ermöglicht.^[25][26]

Weitere wichtige Spektralsequenzen

Topologie und Geometrie

• Atiyah–Hirzebruch-Spektralsequenz einer verallgemeinerte Kohomologietheorie
• Bar-Spektralsequenz für die Homologie des klassifizierenden Raumes einer Gruppe.
• Die Bockstein-Spektralsequenz verknüpft die Homologie mit mod p Koeffizienten und die Homologie mod p.
• Die Cartan-Leray-Spektralsequenz konvergiert gegen die Homologie eines Quotientenraumes.
• Eilenberg-Moore-Spektralsequenz^[27] für die singuläre Kohomologie des Pullbacks einer Faserung

Homotopietheorie

• Adams-Spektralsequenz^[28] in Stabile Homotopietheorie
• Adams-Novikov-Spektralsequenz, eine Verallgemeinerung zur verallgemeinerte Kohomologietheorie.
• Die Barratt-Spektralsequenz konvergiert gegen die Homotopie des Initialraumes einer Kofibration.
• Die Bousfield-Kan-Spektralsequenz konvergiert gegen den Homotopie-Kolimes eines Funktors.
• Chromatische Spektralsequenz zur Berechnung des Initialterms der Adam-Novikov Spektralsequenz.
• Cobar-Spektralsequenz
• Die EHP-Spektralsequenz konvergiert gegen die stabile Homotopygruppe der Sphere
• Die Federer-Spektralsequenz konvergiert gegen die Homotopygruppe eines Funktionenraums.
• Homotopie Fixpunkt Spektralsequenz
• Hurewicz-Spektralsequenz zur Berechnung der Homologie eines Raumes ausgehend von seiner Homotopie.
• Die Miller-Spektralsequenz konvergiert gegen die mod p-stabile Homologie eines Raumes.
• Milnor-Spektralsequenz ist ein anderer Name für die Bar-Spektralsequenz.
• Moore-Spektralsequenz ist ein anderer Name für die Bar-Spektralsequenz.
• Quillen-Spektralsequenz zur Berechnung der Homotopie einer Simplizialgruppe.
• Rothenberg-Steenrod-Spektralsequenz ist ein anderer Name für Bar Spektralsequenz.
• van Kampen-Spektralsequenz zur Berechnung der Homotopie eines Wedges eines Raumes.

Algebra

• Čech-to-abgeleiteter Funktor-Spektralsequenz von Čech-Kohomologie to Garbenkohomologie.
• Veränderung von Rongen-Spektralsequenz zur Berechnung von Tor- und Ext-Gruppen von Moduln.
• Die Connes-Spektralsequenz konvergiert gegen die zyklische Homologie einer Algebra.
• Gersten–Witt-Spektralsequenz
• Green's-Spektralsequenz für Koszul Kohomologie
• Hyperhomologie-Spektralsequenz zur Berechnung von Hyperhomologie.
• Künneth-Spektralsequenz zur Berechnung der Homologie eines Tensorproduktes von Differentialalgebras.
• Die Leray-Spektralsequenz gegen Garbenkohomologie
• Lokal-zo-global Ext-Spektralsequenz
• Lyndon-Hochschild-Serre-Spektralsequenz in Gruppenhomologie
• May-Spektralsequenz von Tor- und Ext-Gruppen einer Algebra
• Universeller-Koeffizienten-Spektralsequenz
• Die van Est-Spektralsequenz konvergiert gegen relative Lie-Algebren-Kohomologie.

Komplexe und algebraische Geometrie

• Arnold's Spektralsequenz in singulärer Theorie.
• Bloch–Lichtenbaum-Spektralsequenz konvergiert gegen die algebraische K-Theorie eines Körpers.
• Die Frölicher-Spektralsequenz beginnt bei der Dolbeault-Kohomologie und konvergiert gegen die algebraische de Rham Kohomologie einer Varietät.
• Die Hodge–de Rham-Spektralsequenz konvergiert gegen die algebraische de Rham Kohomologie einer Varietät.
• Motivik-zu-K-Theorie-Spektralsequenz

Literatur

• Allen Hatcher: Spectral Sequences, Kapitel 5. (cornell.edu [PDF]). 
• Tilman Bauer: Homologische Algebra und Gruppenkohomologie. Vorlesungsskript Wintersemester 2004/05. Universität Münster, 18. Juni 2008, abgerufen am 3. September 2014 (überarbeitete Fassung). 
• Timothy Y. Chow: You could have invented spectral sequences. 2006 (ams.org [PDF]). 
• John McCleary: A User's Guide to Spectral Sequences (= Cambridge studies in advanced mathematics. Nr. 58). 2. Auflage. Cambridge University Press, 2001, ISBN 0-521-56759-9. 
• Henri Cartan, Samuel Eilenberg: Homological Algebra (= Princeton Mathematical Series. Nr. 19). Princeton University Press, 1956, LCCN 53-010148, Kap. XV, XVI. 
• Charles A. Weibel: An introduction to homological algebra (= Cambridge studies in advanced mathematics. Nr. 38). Cambridge University Press, 1994, ISBN 0-521-43500-5, Kap. 5. 
• Serge Lang: Graduate Texts in Mathematics. Springer Verlag, 2002. 
• J. Michael Boardman: Homotopy Invariant Algebraic Structures: A Conference in Honor of J. Michael Boardman : AMS Special Session on Homotopy Theory, January 7-10, 1998. 1999. 

Weblinks

• spectral sequence. Abgerufen am 24. September 2021. 
• multiplicative spectral sequence. Abgerufen am 20. September 2021. 
• Spektralfolgen. Abgerufen am 17. August 2021. 

Einzelnachweise