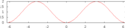
Sinus versus und Kosinus versus
Sinus versus (auch Sinusversus, Quersinus, Versinus oder Versus, in Formeln abgekürzt ) und der Kosinus versus (auch Koversinus oder Querkosinus, in Formeln abgekürzt ) sind in der Trigonometrie heute selten verwendete trigonometrische Funktionen. Semiversus (englisch haversine, in Formeln abgekürzt ) ist der halbe Sinus versus.
Sinus versus
Der Sinus versus bildet zusammen mit dem Kosinus einen Radius 1 (),
der Kosinus versus zusammen mit dem Sinus einen Radius 1 ().
Der Sinus versus wird mit Hilfe der Kosinus- oder Sinusfunktion definiert als[1]
Er ist die Differenz des Kosinus zu +1 (in nebenstehender Abbildung in der Farbe Grün eingezeichnet).
Der Sinus versus kann auf die ganze komplexe Zahlenebene ausgeweitet werden.
Semiversus
Der Semiversus ist die Hälfte des Sinus versus:[2]
Kosinus versus
Der Kosinus versus ist in nebenstehender Abbildung in der Farbe Cyan und als cvs eingezeichnet.
Er ist die Differenz des Sinus zu +1 und auch der Sinus versus des Gegenarguments (π/2 − θ).[3]
Verwandte Funktionen
Manchmal wird analog zu und unter vercos etwas anderes verstanden als unter coversin und unter covercos etwas anderes als unter versin. In folgender Tabelle sind die Funktionen zusammen mit einigen verwandten trigonometrischen Funktionen und dem grafischen Funktionsverlauf zusammengefasst:
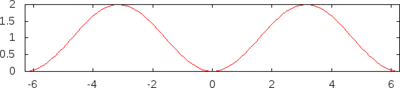 | |
 | |
 | |
 | |
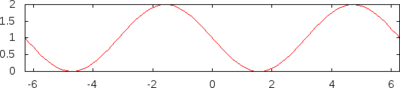 | |
 | |
 | |
 |
Die Ableitungen und die Stammfunktionen sind:
Geschichte und Verwendung
Der Seiten-Kosinussatz der sphärischen Trigonometrie spielte für die nautische Navigation nach den Sternen in früherer Zeit eine wichtige Rolle.[4] Um die dabei erforderlichen Multiplikationen trigonometrischer Funktionen durch das Nachschlagen von Tabellenwerten[5] zu vereinfachen, wurde der Semiversus eingeführt.
Es ergibt sich daraus unter anderem damit der Seiten-Kosinussatz zu:
Literatur
- M. Abramowitz, I. A. Stegun: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York, Dover 1972, S. 78 (Online).
Einzelnachweise
- ↑ Eric W. Weisstein: Versine. In: MathWorld (englisch).
- ↑ Eric W. Weisstein: Haversine. In: MathWorld (englisch).
- ↑ Eric W. Weisstein: Coversine. In: MathWorld (englisch).
- ↑ Bobby Schenk: Astronavigation: ohne Formeln - praxisnah. 2. Auflage. Delius Klasing & Co., Bielefeld 1978.
- ↑ Otto Fulst: Nautische Tafeln. Hrsg.: Johannes Lütjen, Walter Stein, Gerhard Zwiebler. 24. Auflage. Arthur Geist Verlag, Bremen 1972, 17–18.
Auf dieser Seite verwendete Medien
Plot of the coversin function.
Plot of the hacovercosin function.
Plot of the hacoversin function.
Plot of the havercosin function.
Plot of the haversin function.
Plot of the covercosin function.
Autor/Urheber:
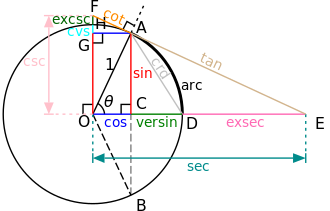
This is a graphical construction of the various trigonometric functions from a chord AD (angle θ) of the unit circle centered at O. In addition to the modern trigonometric functions sin (sine), cos (cosine), tan (tangent), cot (cotangent), sec (secant), and csc (cosecant), the diagram also includes a few trigonometric functions that have fallen into disuse: chord, versin (versine or versed sine), exsec (exsecant), cvs (coversine), and excsc (excosecant).
Plot of the versin function.
Plot of the vercosin function.