S3 (Gruppe)

Die symmetrische Gruppe ${\displaystyle S_{3}}$ bezeichnet im mathematischen Teilgebiet der Gruppentheorie eine bestimmte Gruppe mit 6 Elementen. Sie lässt sich beschreiben als Gruppe der sechs Permutationen einer dreielementigen Menge. Alternative Bezeichnungen sind ${\displaystyle {\mathfrak {S}}_{3}}$ und ${\displaystyle \mathop {\mathrm {Sym} } \nolimits _{3}}$. Sie ist isomorph mit der Dïedergruppe ${\displaystyle D_{3}}$ , der Gruppe der Kongruenzabbildungen des gleichseitigen Dreiecks auf sich.

Einführung

Die Wirkungen der Abbildungen ${\displaystyle d}$, ${\displaystyle d^{2}}$, ${\displaystyle s_{1}}$, ${\displaystyle s_{2}}$ und ${\displaystyle s_{3}}$

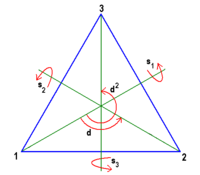
Betrachtet man die Kongruenzabbildungen, die ein gleichseitiges Dreieck in sich selbst überführen, so findet man 6 Möglichkeiten:^[1]

• die identische Abbildung ${\displaystyle e}$,
• die Drehung ${\displaystyle d}$ um 120° um den Mittelpunkt des Dreiecks,
• die Drehung ${\displaystyle d^{2}}$ um 240° um den Mittelpunkt des Dreiecks,
• die drei Spiegelungen ${\displaystyle s_{1},s_{2}}$ und ${\displaystyle s_{3}}$ an den drei Mittelsenkrechten des Dreiecks.

Diese Kongruenzabbildungen lassen sich durch Hintereinanderausführung kombinieren, wodurch man wieder eine Kongruenzabbildung erhält. Man schreibt einfach zwei Kongruenzabbildungen (oft ohne Verknüpfungszeichen, oder mit ${\displaystyle \cdot }$ oder ${\displaystyle \circ }$) nebeneinander und meint damit, dass

zuerst die rechtsstehende und dann die linksstehende

Kongruenzabbildung auszuführen ist.^[2] Die Schreibweise ${\displaystyle d^{2}}$ macht bereits deutlich, dass die Drehung um 240° gleich der zweifachen Hintereinanderausführung der Drehung um 120° ist.

Man erhält auf diese Weise die sechselementige Gruppe ${\displaystyle S_{3}=\left\{e,d,d^{2},s_{1},s_{2},s_{3}\right\}}$ aller Kongruenzabbildungen des gleichseitigen Dreiecks auf sich. Trägt man alle so gebildeten Verknüpfungen in eine Verknüpfungstafel ein, so erhält man

Will man das Produkt ${\displaystyle ba}$^[2] für zwei Elemente ${\displaystyle a,b}$ aus ${\displaystyle S_{3}}$ ausrechnen, so suche man in der Verknüpfungstafel zuerst die mit ${\displaystyle a}$ gekennzeichnete Spalte, dann die mit ${\displaystyle b}$ gekennzeichnete Zeile auf; am Schnittpunkt dieser Spalte und Zeile steht das Produkt.

Verallgemeinert man diese Konstruktion, indem man das gleichseitige Dreieck durch ein regelmäßiges ${\displaystyle n}$-Eck ersetzt, so kommt man zum Begriff der Diedergruppe. Daher wird die hier besprochene Gruppe ${\displaystyle S_{3}}$ auch mit ${\displaystyle D_{3}}$ bezeichnet.

Elemente der S₃ als Permutationen

Eine Kongruenzabbildung des gleichseitigen Dreiecks ist bereits dadurch eindeutig festgelegt, wie die mit 1, 2 und 3 bezeichneten Ecken aufeinander abgebildet werden. Jedes Element der ${\displaystyle S_{3}}$ kann daher als Permutation der Menge ${\displaystyle \{1,2,3\}}$ aufgefasst werden. Im Folgenden ist zuerst die Zweizeilenform angegeben, dahinter die Zyklenschreibweise^[3] der Elemente sowie deren Ordnungen:

Eigenschaften

Keine abelsche Gruppe

Die Gruppe ${\displaystyle S_{3}}$ ist keine abelsche Gruppe, wie obiger Verknüpfungstafel entnommen werden kann (sie ist nicht symmetrisch zur Hauptdiagonale); beispielsweise gilt ${\displaystyle s_{2}s_{1}=d^{2}\neq d=s_{1}s_{2}}$. Sie ist bis auf Isomorphie die kleinste nicht-abelsche Gruppe, das heißt, jede nicht-abelsche Gruppe ist entweder isomorph zu ${\displaystyle S_{3}}$ oder hat mehr Elemente.

Untergruppen und Normalteiler

Die Untergruppen neben den trivialen Untergruppen ${\displaystyle \{e\}}$ und ${\displaystyle S_{3}}$ selbst sind:

• ${\displaystyle A_{3}:=\left\{e,d,d^{2}\right\}\cong \mathbb {Z} /3\mathbb {Z} }$. Diese Untergruppe (die Gruppe der Drehungen) ist ein Normalteiler und wird auch als alternierende Gruppe vom Grad 3 bezeichnet.
• ${\displaystyle \{e,s_{1}\}\cong \{e,s_{2}\}\cong \{e,s_{3}\}\cong \mathbb {Z} /2\mathbb {Z} }$. Diese Untergruppen (die Gruppen der Spiegelungen) sind keine Normalteiler; beispielsweise ist ${\displaystyle d\{e,s_{1}\}d^{-1}\,=\,d\{e,s_{1}\}d^{2}\,=\,\{e,s_{2}\}}$.
• Das Zentrum von ${\displaystyle S_{3}}$ ist trivial (besteht nur aus ${\displaystyle \{e\}}$). Somit kommutiert ein von ${\displaystyle e}$ verschiedenes Element nur mit Potenzen seiner selbst.

Erzeuger und Relationen

Man kann Gruppen auch dadurch beschreiben, dass man ein Erzeugendensystem und Relationen, die die Erzeuger erfüllen müssen, angibt. Erzeuger und Relationen notiert man, durch das Zeichen  ${\displaystyle \mid }$  getrennt, in spitzen Klammern. Die Gruppe ist dann die von den Erzeugern erzeugte freie Gruppe modulo dem von den Relationen erzeugten Normalteiler. In diesem Sinne ist:^[4]

${\displaystyle S_{3}=\langle d,s\mid d^{3},s^{2},dsds\rangle }$

Irreduzible Darstellungen

Bis auf Äquivalenz hat die ${\displaystyle S_{3}}$ drei irreduzible Darstellungen, zwei eindimensionale und eine zweidimensionale.^[5] Zur Angabe dieser Darstellungen genügt es, die Bilder von ${\displaystyle d}$ und ${\displaystyle s_{1}}$ anzugeben, denn diese Elemente erzeugen die Gruppe.

• Die triviale Darstellung: ${\displaystyle S_{3}\rightarrow \mathbb {C} :\,\,d\mapsto 1,s_{1}\mapsto 1}$
• Die Signum-Abbildung: ${\displaystyle S_{3}\rightarrow \mathbb {C} :\,\,d\mapsto 1,s_{1}\mapsto -1}$
• Die zweidimensionale Darstellung: ${\displaystyle S_{3}\rightarrow M_{2}(\mathbb {C} ):\,\,d\mapsto {\begin{bmatrix}e^{2\pi i/3}&0\\0&e^{-2\pi i/3}\end{bmatrix}},s_{1}\mapsto {\begin{bmatrix}0&1\\1&0\end{bmatrix}}}$.

Zwar erhält man eine andere zweidimensionale Darstellung, wenn man ${\displaystyle s_{1}}$ durch ${\displaystyle s_{2}}$ ersetzt, aber diese ist äquivalent zur angegebenen. Diese Überlegungen führen zu folgender Charaktertafel:^[6]

Weitere Beispiele

Allgemeine lineare Gruppe über ℤ/2

Die allgemeine lineare Gruppe 2-ten Grades über dem Restklassenkörper ${\displaystyle \mathbb {Z} /2=\mathbb {F} _{2}=\{0,1\}}$, ${\displaystyle GL(2,\mathbb {F} _{2})=\left\{{\begin{bmatrix}1&0\\0&1\end{bmatrix}},{\begin{bmatrix}1&1\\0&1\end{bmatrix}},{\begin{bmatrix}1&0\\1&1\end{bmatrix}},{\begin{bmatrix}0&1\\1&0\end{bmatrix}},{\begin{bmatrix}1&1\\1&0\end{bmatrix}},{\begin{bmatrix}0&1\\1&1\end{bmatrix}}\right\}}$ ist isomorph zur ${\displaystyle S_{3}}$.

Transformationengruppe

Die gebrochen linearen Funktionen ${\displaystyle s_{1},s_{2}}$ mit Koeffizienten aus einem beliebigen Körper ${\displaystyle K}$ und den Zuordnungen^[7]

erzeugen mit der Hintereinanderausführung als Gruppenverknüpfung eine Gruppe ${\displaystyle G}$, die isomorph zur ${\displaystyle S_{3}}$ ist. Die übrigen 4 Gruppenmitglieder sind:

Die Verknüpfungstafel ist wie oben.
Die 6 Gruppenmitglieder ${\displaystyle s\in G}$ unterscheiden sich bei einer Einsetzung von Elementen ${\displaystyle x\in K\!\setminus \!\{0,1\}}$

${\displaystyle s_{K}:x\mapsto s_{K}(x):=s(x)}$

auch in den Wertetabellen, wenn ${\displaystyle K}$ wenigstens 5 Elemente hat.

Automorphismengruppe

Die ${\displaystyle S_{3}}$ ist isomorph zur Automorphismengruppe der Kleinschen Vierergruppe. Das ergibt sich leicht aus der Beobachtung, dass jede Permutation der drei Elemente der Ordnung 2 der Kleinschen Vierergruppe einen Automorphismus definiert.

Siehe auch

• Liste kleiner Gruppen

Weblinks

• Applet der TU München zur Visualisierung von ${\displaystyle S_{3}}$

Einzelnachweise

1. ↑ Arno Mitschka: Elemente der Gruppentheorie. Studienbücher Mathematik, 1975, ISBN 3-451-16528-7, Abschnitt II.5
2. ↑ ^{a b} Diese Reihenfolge kommt von der Operatorenperspektive, wie sie bei der Hintereinanderschaltung von Abbildungen (so auch bei den Permutationen) vorherrscht. Für die pure Gruppentheorie ist die Reihenfolge unerheblich.
3. ↑ K. Meyberg: Algebra, Teil I. Carl Hanser Verlag, 1980, ISBN 3-446-13079-9, Beispiel 2.4.2.c
4. ↑ K. Meyberg: Algebra, Teil I. Carl Hanser Verlag, 1980, ISBN 3-446-13079-9, Beispiel 2.7.18.c
5. ↑ J. P. Serre: Darstellungen endlicher Gruppen. Vieweg, 1972, ISBN 3-528-03556-0, §5.3
6. ↑ Kurt Meyberg: Algebra II. Carl Hanser Verlag, 1976, ISBN 3-446-12172-2, Beispiel 9.7.1 b
7. ↑ Ist ${\displaystyle K}$ der Körper der komplexen Zahlen, genauer: die riemannsche Zahlenkugel, dann handelt es sich um Möbiustransformationen.