Rotationsverfahren (Statistik)

Als Rotationsverfahren oder Rotationsmethode bezeichnet man in der multivariaten Statistik eine Gruppe von Verfahren, mit denen Koordinatensysteme so lange gedreht werden können, bis sie ein zuvor definiertes Kriterium erfüllen. Die Räume, in denen sich diese Koordinatensysteme befinden, stellen keine speziellen Anforderungen. Sie sind beliebig n-dimensional, idealerweise jedoch metrisch.

Einsatz von Rotationsverfahren

Rotationsverfahren werden oft in Verbindung mit der Faktorenanalyse oder Hauptkomponentenanalyse als Interpretationshilfe eingesetzt.

Dabei wird wie folgt vorgegangen: Nachdem mit der Extraktionsmethode Faktoren ermittelt wurden, welche die Varianz der Variablen aufklären, wird mit der Rotation versucht, die Faktoren den Daten „entgegen zu drehen“, bis nur noch wenige Faktoren mit hoher Ladung übrig sind. Diese lassen sich dann eindeutiger hypothetischen Gesetzmäßigkeiten zuordnen, was als Interpretationshilfe bezeichnet wird. Dies ist nötig, da die erste errechnete Faktorlösung oft nur schwer interpretierbar ist. Meist wird eine Einfachstruktur angestrebt, d. h. die Drehung so vorgenommen, dass die einzelnen Variablen lediglich auf einem Faktor hoch laden (meist ein Wert von 0.5) und sonst auf keinem Faktor. Die Einfachstruktur ist aber nur ein angestrebtes Ziel, das keinesfalls erreicht werden muss.^[1]

Die Rotation erhöht den aufgeklärten Varianzanteil nicht. Sie hilft lediglich, die Faktoren inhaltlich besser zu verstehen.

Ausgewählte Rotationsverfahren

Orthogonale Faktorrotation.

Nach einer obliquen Rotation können die Achsen schiefwinklig aufeinander stehen.

Rotationsverfahren werden danach unterschieden, ob sie orthogonal oder schief (oblique) sind. Die gängigste Methode ist Varimax. Andere orthogonale Rotationsverfahren sind Quartimax sowie Equamax (auch Equimax^[2]), das eine Kombination aus Varimax und Quartimax darstellt.

Daneben existieren auch schiefwinklige Rotationsverfahren wie Oblimin und Promax, die die Annahme der Orthogonalität der Faktoren lockern.^[2] Diese Verfahren werden eher aus praktischen Gründen genutzt und sind manchmal durch erheblich verbesserte Interpretierbarkeit motiviert. Im mathematisch-formalen Sinne sind sie z. B. im orthogonalen Faktorenmodell nicht erlaubt, da dies nur bis auf orthogonale Transformationen eindeutig ist. Hier würde also zugunsten einer leichten Interpretierbarkeit sogar das Prinzip unkorrelierter Faktoren aufgegeben.

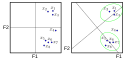
Die nebenstehende Abbildung verdeutlicht das orthogonale Rotationsvorgehen. Im ersten Teil der Abbildung (z. B. der ersten nicht rotierten Faktorlösung) laden alle Variablen sehr ähnlich auf den ersten Faktor, was eine Interpretation erschwert. Ziel ist es, das Achsenkreuz so zu drehen, dass möglichst viele der Variablen betragsmäßig hohe Werte in einer Koordinate und Werte nahe Null in der anderen Koordinate bekommen. Nach der Rotation bilden die Variablen ${\displaystyle X_{1},X_{2},X_{3}}$ eine Gruppe die hoch auf Faktor 2 lädt und kaum auf Faktor 1. Eine andere Gruppe für Faktor 1 wurde ebenfalls grün gekennzeichnet. Die Beobachtung ${\displaystyle X_{4}}$ stellt einen Ausreißer dar.

Die gebräuchliche Varimax-Methode wird im Folgenden genauer vorgestellt.

Varimax

(c) Dalmer at da.wikipedia, CC BY-SA 3.0

Die Methoden Varimax und Oblimin im Vergleich.

Als Varimax bezeichnet man eine mathematische Rechenmethode, mit der sich Koordinatensysteme in n-dimensionalen Räumen drehen lassen. Die von Henry Felix Kaiser Ende der 1950er Jahre entwickelte Methode wird überwiegend bei statistischen Verfahren eingesetzt und spielt insbesondere bei der Faktorenanalyse eine wichtige Rolle als inhaltliche Interpretationshilfe.

Vorgehensweise

Varimax wird den Rotationsverfahren zugeordnet. Bei der Anwendung in Verbindung mit der Faktorenanalyse werden die Faktoren in fortlaufenden Schritten so lange im Raum gedreht, bis die Varianz der quadrierten Ladungen pro Faktor maximal ist. Dadurch erhielt dieses Verfahren auch seinen Namen. Mittelgroße Ladungen werden also entweder geringer oder stärker und können damit eindeutiger ihren jeweiligen Faktoren zugeordnet werden. Dabei wird ein orthogonales Design benutzt, weil die Befürworter dieses Verfahrens davon ausgehen, dass die latenten Faktoren voneinander unabhängig sind.

Geometrisch gesehen werden die (orthogonalen) Koordinatenachsen gegenüber den alten Achsen im Raum verdreht, wobei der Ursprung der Achsen gleich bleibt. Aus dem Kosinus der Winkel zwischen den Faktoren und den ursprünglichen Koordinatenachsen wird die Komponententransformationsmatrix gebildet. Durch die Multiplikation dieser Matrix mit der unrotierten Faktorladungsmatrix können die rotierten Faktorladungen berechnet werden:

${\displaystyle {\underline {K}}^{*}={\underline {L}}\cdot {\underline {T}}}$.

• ${\displaystyle K^{*}}$: Matrix der rotierten Faktorladungen
• ${\displaystyle L}$: Matrix der unrotierten Faktorladungen
• ${\displaystyle T}$: Komponententransformationsmatrix

Literatur

• H. F. Kaiser: Computer program for varimax rotation in factor analysis. In: Educational and Psychological Measurement. 19, 1959, S. 413–420. doi:10.1177/001316445901900314
• W. Schiller: Vom sinnvollen Aufwand in der Faktorenanalyse. In: Archiv für Psychologie. 140, 1988, S. 73–95. (u. a. Vergleich verschiedener Rotationsverfahren)
• H. F. Kaiser: The varimax criterion for analytic rotation in factor analysis. In: Psychometrika. 23, 1958, S. 187–200. doi:10.1007/BF02289233

Einzelnachweise

1. ↑ Explorative Faktorenanalyse – Methodenvorstellung von Eric Klopp
2. ↑ ^{a b} Marcus J. Schmidt, Svend Hollensen: Marketing research: an international approach. Pearson, 2006, S. 312.