Riemannsche Zeta-Funktion


Die Riemannsche Zeta-Funktion, auch Riemannsche ζ-Funktion oder Riemannsche Zetafunktion (nach Bernhard Riemann), ist eine komplexwertige, spezielle mathematische Funktion, die in der analytischen Zahlentheorie, einem Teilgebiet der Mathematik, eine wichtige Rolle spielt. Erstmals betrachtet wurde sie im 18. Jahrhundert von Leonhard Euler, der sie im Rahmen des Basler Problems untersuchte. Bezeichnet wird sie üblicherweise mit dem griechischen Buchstaben (Zeta).
Ihr Definitionsbereich umfasst alle komplexen Zahlen außer der Zahl . Für Werte mit Realteil größer als wird die Riemannsche Zeta-Funktion über eine Dirichlet-Reihe definiert. Sie lautet:
für .
Mittels analytischer Fortsetzung kann sie zu einer auf holomorphen Funktion ausgeweitet werden. Sie erfüllt eine wichtige Funktionalgleichung, mit deren Hilfe sie sogar charakterisiert werden kann.
Von großer Bedeutung für die Zahlentheorie ist der Zusammenhang der Zeta-Funktion mit der Primfaktorzerlegung natürlicher Zahlen. Auf dieser Basis konnte Riemann im Jahr 1859 die sehr enge und nicht offensichtliche Beziehung zwischen den Primzahlen und der Lage der Nullstellen der Zeta-Funktion nachweisen. So folgt aus der Tatsache für alle komplexen Zahlen mit bereits, dass die -te Primzahl „recht genau“ den Wert hat – genauer gesagt folgt[1][2]
Hier bezeichnet den natürlichen Logarithmus von . Genauere Informationen über nullstellenfreie Bereiche macht das Bild um die Primzahlverteilung deutlicher. Die bisher unbewiesene Riemannsche Vermutung sagt aus, dass alle nicht-trivialen Nullstellen der Riemannschen Zeta-Funktion den Realteil haben, also auf einer gemeinsamen Geraden liegen. Ob diese Vermutung zutrifft, ist eines der wichtigsten ungelösten Probleme der Mathematik. Aufgrund der Bedeutung der Primzahlen für moderne Kryptosysteme (wie in etwa der RSA-Verschlüsselung) genießt die Riemannsche Vermutung auch außerhalb der reinen Zahlentheorie Aufmerksamkeit.
Das Verhalten der Riemannschen Zeta-Funktion in den Bereichen und gilt als gut verstanden. Jedoch sind ihre Eigenschaften innerhalb des kritischen Streifens weitestgehend unbekannt und Gegenstand bedeutender Vermutungen. Dies betrifft unter anderem die Fragen nach asymptotischem Wachstum in imaginärer Richtung und der für die Zahlentheorie so wichtigen Nullstellenverteilung. Nach heutigem Wissensstand beschreibt die Zeta-Funktion im Streifen im Wesentlichen Chaos. Die Werte der Nullstellen bauen nicht nur Brücken zur Theorie der Primzahlen, sondern höchstwahrscheinlich auch zur modernen Quantenphysik. Weitere Anwendungsgebiete sind die Wahrscheinlichkeitstheorie und die Theorie der automorphen Formen (insbesondere im Feld des Langlands-Programms).
Aus Sicht der algebraischen Zahlentheorie ist die Riemannsche Zeta-Funktion nur ein Spezialfall einer ganzen Klasse sogenannter L-Funktionen. So entspricht sie der zum Trivialen Charakter modulo 1 gehörigen Dirichletschen L-Funktion und der zum Zahlkörper (rationale Zahlen) korrespondierenden Dedekindschen Zeta-Funktion.
Wegen der überragenden Bedeutung der Riemannschen Vermutung für die Zahlentheorie und deren Anwendungen bleibt der Themenkreis der Riemannschen Zeta-Funktion ein Gebiet intensiver mathematischer Forschung. Entscheidende Fortschritte erzielten Mathematiker wie zum Beispiel Lindelöf, Hadamard, de La Vallée Poussin, Hardy, Littlewood, Selberg, Woronin und Conrey.
Notation
Im ganzen Artikel bezeichnet die imaginäre Einheit und die Eulersche Zahl. Zudem wird häufig als komplexe Variable verwendet, die oft in zerlegt wird.
Des Weiteren wird oft die O-Notation von Landau für die Angabe von Fehlergrößen verwendet. Verhalten sich zwei (unbeschränkte) Funktionen und für wachsendes Argument gleich, gilt also , so wird dies mit notiert.
Einordnung ohne mathematisches Vorwissen
Motivation


Im Zentrum der Zahlentheorie, jenes Zweiges der Mathematik, der sich mit den Eigenschaften der natürlichen Zahlen 1, 2, 3, 4 … beschäftigt, stehen die Primzahlen 2, 3, 5, 7, 11 … Diese sind ausgezeichnet durch die Eigenschaft, genau zwei Teiler zu haben, nämlich die 1 und sich selbst. Die 1 ist keine Primzahl. Bereits Euklid konnte zeigen, dass es unendlich viele Primzahlen gibt, weshalb die Liste 2, 3, 5, 7, 11 … niemals enden wird.
Die Primzahlen sind gewissermaßen die Atome der ganzen Zahlen, da sich jede positive ganze Zahl eindeutig multiplikativ in solche zerlegen lässt. Zum Beispiel gilt 21 = 3 · 7 und 110 = 2 · 5 · 11. Trotz dieser elementaren Eigenschaft ist nach mehreren Jahrtausenden Mathematikgeschichte bis heute kein Muster bekannt, dem sich die Primzahlen in ihrer Folge unterwerfen. Ihre Natur ist eine der bedeutendsten offenen Fragen der Mathematik.
Auch wenn das detaillierte Verständnis der Sequenz 2, 3, 5, 7, 11 … unerreichbar fern ist, kann man nach Mustern suchen, wenn man den Blick ausweitet. Dabei hilft zum Beispiel die Vorstellung, dass mit Hilfe statistischer Methoden das Verhalten sehr vieler Menschen (zum Beispiel bezüglich des Konsum- und Wahlverhaltens) oft überraschend präzise beschrieben werden kann, obgleich ein einzelner Mensch äußerst komplex ist. Das hat grob gesagt damit zu tun, dass größer werdende relevante Datenmengen immer zuverlässigere Informationen liefern.[3] Im Falle der Primzahlen führt eine solche Ausweitung unter anderem zu der Frage, wie viele Primzahlen es unterhalb einer fest gewählten Zahl gibt.
Zum Beispiel sind nur 4 Primzahlen, nämlich 2, 3, 5 und 7, kleiner als die Zahl 10. Im Falle von 50 gibt es schon 15 kleinere Primzahlen, nämlich
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
Ende des 19. Jahrhunderts konnte als Folgerung des Primzahlsatzes eine verblüffend genaue Abschätzung für die Verteilung der Primzahlen bewiesen werden. Der Primzahlsatz wurde bereits im 18. Jahrhundert vom 15-jährigen Gauß (in den Jahren 1792/93) vermutet.[4] Die Abschätzung wurde bereits vor einem Beweis des Primzahlsatzes von Riemann gegeben und tritt als eine Formel in Erscheinung, die die schnelle Berechnung eines Vorhersagewertes zulässt. Mit dieser Formel kann zu einer gegebenen Zahl die Anzahl der Primzahlen, die kleiner als diese Zahl sind, in vernünftiger Zeit geschätzt werden. Die Formel zur Vorhersage wird prozentual immer genauer, je größer die Zahl gewählt wird (jedoch mit Schwankungen). Beispielsweise liefert sie für den Wert 50 die Prognose 14,97 (es sind tatsächlich 15 Primzahlen, siehe oben), womit der Fehler bei 0,16 Prozent liegt. Weiter sagt sie rund 78.527 Primzahlen unter der Zahl 1.000.000 voraus – tatsächlich sind es 78.498. Dies entspricht einer Abweichung von 0,037 Prozent.
Ein mögliches Werkzeug zum Beweis dieser Formel ist die Riemannsche Zeta-Funktion. Dabei wird ausgenutzt, dass sie das Gesetz der eindeutigen Primfaktorzerlegung in der Sprache der Analysis ausdrückt. Also werden die Eigenschaften der Primzahlen in dieser Funktion versteckt abgespeichert. Erhöht sich das Wissen um die Zeta-Funktion, so auch das Wissen um die Primzahlen, sogar in detaillierteren Fragestellungen. So können viele Primzahltests, wie der von Miller-Rabin unter Annahme der Riemannschen Vermutung bewiesen bzw. verbessert werden.[5]
Die Nullstellen der Zeta-Funktion erzeugen einen Korrekturterm obiger Formel, der sie in einen exakten Ausdruck umwandelt. Diese dadurch entstehende exakte Formel kennt also die Verteilung der Primzahlen bis ins letzte Detail. Damit gelten die Fragen um die Primzahlen jedoch nicht als gelöst: der Rechenaufwand nimmt mit steigenden Werten sehr stark zu und somit sind praktische Berechnungen mit dieser Formel nicht effektiv. Für numerische Forschung eignen sich im Gegensatz dazu moderne Primzahltests besser. Die exakte Formel ist jedoch von theoretischem Interesse: sie birgt nämlich den Fehlerabstand zwischen der einfachen Vorhersage und der tatsächlichen Primzahlverteilung. Es wird vermutet, dass dieser Fehler (innerhalb des Spektrums aller Möglichkeiten) kleinstmöglich ist. Dabei wäre eine Entschlüsselung dieses Fehlers nicht so sehr für die Numerik von Relevanz. Vielmehr ist die reine Mathematik bestrebt, den bisher verborgenen Grund zu erfahren, weshalb der Fehler (falls zutreffend) so klein wie möglich ausfällt.
Die Primzahlen sind nicht nur Gegenstand der mathematischen Grundlagenforschung, sondern haben auch praktische Anwendungen. So kommen beispielsweise bei Kryptosystemen wie der RSA-Verschlüsselung sehr große Primzahlen zum Einsatz.
Wie „funktioniert“ die Zeta-Funktion?
Eine mathematische Funktion ist im Grunde wie eine Rechenmaschine. Man gibt einen Wert in die Funktion ein, und diese liefert dann ein Ergebnis in Abhängigkeit vom Eingabewert, zumindest theoretisch. Damit ist gemeint, dass die Funktion an sich nicht rechnet, sondern meist nur eine Rechenvorschrift formelhaft festhält. Einfaches Beispiel für eine Funktion ist die quadratische Funktion, welche die Eingabe mit sich selbst multipliziert. Formelhaft schreibt man dies als . Somit ordnet die quadratische Funktion beispielsweise der Zahl den Wert zu. Rechnet man dies aus, ergibt sich , also .
Im Prinzip funktioniert die Riemannsche Zeta-Funktion genau wie das obere Beispiel, nur dass die Rechenvorschrift etwas komplizierter ist. Um diese zu verstehen, muss das Konzept der unendlichen Reihen bekannt sein. Eine (konvergente) Reihe ist grob gesagt eine Summe von Zahlen, die niemals endet und die sich einer Zahl immer mehr annähert. Ein elementares nicht-triviales Beispiel einer Reihe fußt auf der Zahl , die in Dezimalschreibweise nicht geschlossen, sondern nur durch die unendliche periodische Entwicklung
geschrieben werden kann. Schaut man genauer hin, sieht man, dass dies gerade die Summe aller kehrwertiger 10er-Potenzen ist:
Damit sich die unendlich lange Summe einem Wert annähert, muss gewährleistet sein, dass die Summanden „schnell genug klein“ werden.
Die Riemannsche Zeta-Funktion ist nun vergleichbar mit einer Rechenmaschine, die zu einer gegebenen Zahl die unendliche Summe der Kehrwerte aller natürlichen Potenzen mit diesem Exponenten bildet. Als mathematische Formel lautet diese Vorschrift
- .
Um das besser zu verstehen, betrachtet man das Beispiel der Eingabe . Die natürlichen Potenzen mit diesem Exponenten sind gerade die Quadratzahlen 1, 4, 9, 16, 25 … . Damit wäre das Ergebnis der Zeta-Rechenmaschine in Abhängigkeit vom Eingabewert 2 die Reihe
Es stellt sich heraus, dass die Ausdrücke schnell genug klein werden, so dass diese unendlich lange Summe sich einem gewissen Zahlenwert beliebig annähert, je weiter man summiert. Experimentell kann man festhalten:
und wenn man sogar bis zur millionsten Quadratzahl geht
Da hier bereits sehr viele Terme addiert wurden, kann man vermuten, dass dem exakten Ergebnis schon recht nahe ist. Der exakte Grenzwert ist, das konnte Leonhard Euler begründen, die Zahl
- .
Dabei ist die Kreiszahl. Zwar kannte Euler den Beginn der Dezimalfolge , doch seine Begründung beruhte letztlich auf mathematischen Argumenten und nicht expliziten Rechnungen, da die Summe ja niemals endet. Somit liefert die Zeta-Funktion für die Eingabe 2 das Ergebnis . Analog müssen für die Eingabe 3, 4 … usw. entsprechend die Kehrwerte aller Kubikzahlen, Biquadratzahlen usw. addiert werden und es kommen neue Grenzwerte , … usw. zustande.
Definition und Darstellungsformen
Dirichlet-Reihe
Die Zeta-Funktion wird in der Literatur oft über ihre Darstellung als Dirichlet-Reihe definiert.
Für komplexe Zahlen , deren Realteil größer als 1 ist, ist die Zeta-Funktion definiert durch die Dirichlet-Reihe[6]
Wie man mittels des Integralkriteriums für unendliche Reihen zeigen kann, ist diese Reihe im angegebenen Bereich absolut konvergent. Zudem ist die Konvergenz auf kompakten Teilmengen gleichmäßig, weshalb nach dem Satz von Weierstraß die dargestellte Funktion holomorph ist. Wegen der Divergenz der harmonischen Reihe ist diese Darstellung für alle komplexen Zahlen mit Realteil kleiner oder gleich 1 jedoch ungültig. In besonderem Maße wird dies für negative Argumente ersichtlich, wenn man zum Beispiel versuchte, die Zeta-Funktion für über die Dirichlet-Reihe auszuwerten. Man hätte dann
und diese Reihe hat offensichtlich keinen endlichen Grenzwert.
Dennoch wird die Dirichlet-Reihe aufgrund ihrer Einfachheit und ihrer zahlentheoretischen Relevanz (siehe Euler-Produkt) als Basisdefinition verwendet. Mittels analytischer Fortsetzung (siehe unten) wird eine sinnvolle Berechnung für alle komplexen Zahlen mit möglich. Damit kann schließlich auch Werten wie ein Sinn gegeben werden, es gilt zum Beispiel .
Euler-Produkt
Eine wesentliche Eigenschaft der Zeta-Funktion ist ihre Verbindung zu den Primzahlen. Euler, der als Erster diesen Zusammenhang entdeckte, betrachtete dafür das später nach ihm benannte Euler-Produkt, das für alle mit gültig ist:[6]
Es ist genau äquivalent zur Dirichlet-Reihe und wird von manchen Autoren als Definition verwendet.[7][8] Jeder einzelne Faktor des Produktes stellt eine geometrische Reihe gebildet über den Wert dar, während sich das ganze Produkt über alle Primzahlen erstreckt. Das Euler-Produkt ist erstaunlich, weil Primzahlen aufgrund ihrer nicht genau vorhersehbaren Verteilung sehr schwer in analytischen Ausdrücken unterzubringen sind. Es stellt sich aber eine überraschend einfache Identität zwischen den „chaotischen“ Primzahlen und einer bekannten Reihe heraus.
| Für die detaillierte Herleitung |
Für die formale Herleitung des Euler-Produktes werden lediglich die geometrische Reihe, der Satz, dass jede natürliche Zahl genau eine Zerlegung als Produkt von Primzahlen besitzt, sowie Ausmultiplizieren von Klammern benötigt. Zu Beginn bewährt es sich, nur eine endliche Anzahl von Primzahlen im Produkt zu beachten. Entwickelt man jeden Term als eine geometrische Reihe , so ergibt sich im Falle nur einer Primzahl wobei das Potenzgesetz zu beachten ist. Zur Rechten stehen genau die Zahlen, die ausschließlich Zweien in ihrer Primfaktorzerlegung haben, also die Zweierpotenzen. Verfährt man weiter mit den ersten zwei Primzahlen, ergibt sich Multipliziert man beide Klammen aus, ergeben sich in der Summe alle Kombinationen von Termen der Form mit , es gilt also und auf der rechten Seite stehen genau alle solchen Terme , sodass nur Zweien und Dreien in seiner Primfaktorzerlegung hat. Beim Ausmultiplizieren wird jeder Summand der einen Klammer mit einem Summand der anderen Klammer verrechnet, und das in jeder Kombination, für sind die entsprechenden Terme in Rot markiert. Auf ähnliche Weise findet man, dass zu der entsprechenden Dirichlet-Reihe korrespondiert, in der alle Zahlen mit Primfaktorzerlegung auftauchen, und so weiter. Entsprechend gilt für allgemein die ersten Primzahlen Nun kann man in dieser Formel gegen Unendlich laufen lassen, und erhält da jede Zahl genau eine Zerlegung besitzt. |
Das Euler-Produkt konvergiert im betrachteten Bereich unbedingt.[9] Mittels des Identitätssatzes für Dirichlet-Reihen lässt sich zeigen, dass das Euler-Produkt und der Fundamentalsatz der Arithmetik zueinander äquivalent sind. Daher wird es zuweilen auch als dessen analytische Version bezeichnet.[10] Eine wichtige Folgerung des Euler-Produktes für die Analysis der Zeta-Funktion ist, dass für alle gilt. Dies ist eine Konsequenz einer Erweiterung des Satzes vom Nullprodukt für unendliche Produkte: keiner der Faktoren des Euler-Produktes ist für irgendeinen Eingabewert aus diesem Bereich Null, also wird es auch nicht im Grenzwert Null sein.[11] Weitaus nichttrivialer ist die Tatsache, dass das Euler-Produkt, im Gegensatz zur Dirichlet-Reihe, auch auf der Geraden , mit Ausnahme von , an Gültigkeit behält. Es gilt[12]
was die Nullstellenfreiheit von im gesamten Bereich zur Folge hat. Als eine Folgerung der Funktionalgleichung ergibt sich, dass die einzigen Nullstellen von außerhalb des sog. kritischen Streifens die trivialen Nullstellen
sind. Alle anderen Nullstellen bezeichnet man als nichttrivial, und diese liegen allesamt im kritischen Streifen.[13]
Mithilfe des Euler-Produkts der Zeta-Funktion kann ein Beweis des Satzes von Euklid mit analytischen Methoden angegeben werden. Der Satz von Euklid besagt, dass es unendlich viele Primzahlen geben muss, und wurde etwa 300 Jahre vor Christus durch Euklid von Alexandria bewiesen. Unter der Annahme, es gäbe nur endlich viele Primzahlen, gilt
was ein Widerspruch zur Divergenz der harmonischen Reihe ist. Ähnlich bemerkenswert ist die Argumentation über die Formel
Bei endlich vielen Primzahlen wäre die linke Seite eine rationale Zahl, die rechte Seite ist aber aufgrund der Transzendenz der Kreiszahl irrational.[14]
Eine weitere direkte Folgerung des Euler-Produktes, durch Logarithmieren und anschließende Verwendung der Taylor-Reihe des Logarithmus, ist die für gültige Formel
wobei mit die Primzetafunktion bezeichnet.[15] Mit Hilfe von Möbius-Inversion lässt sich daraus eine Möglichkeit ableiten, die Primzetafunktion schnell aus einer Reihe über logarithmierte Zeta-Funktionen zu gewinnen:[16]
Unter anderem kann dieser Ausdruck für eine schnelle numerische Berechnung der Primzetafunktion herangezogen werden.[17] Ferner folgt aus für , dass die Reihe der reziproken Primzahlen divergiert.
Mellin-Transformation
Die nach der Definition als Dirichlet-Reihe und dem Euler-Produkt wohl elementarste und wichtigste Darstellung der Zeta-Funktion ist die mit Hilfe eines uneigentlichen Integral-Ausdrucks. Auch diese Darstellung geht direkt aus der Dirichlet-Reihe hervor.
Grundlage dieser Darstellung ist die eulersche Integral-Darstellung der Gamma-Funktion
aus dem nach der Substitution mit und Division durch nach beidseitigem Summieren der Ausdruck
hervorgeht.[18] Diese Darstellung von gilt naturgemäß nur auf der Halbebene . Die zweite Integraldarstellung von bezeichnet man auch als die Mellin-Transformation von . Das mögliche Vertauschen von Summe und Integral kann mit absoluter Konvergenz und dem Satz von Lebesgue begründet werden. Eine dazu verwandte Form ist
mit der Jacobischen Theta-Funktion (eine Modulform halbganzen Gewichts).
Die Darstellung der Zeta-Funktion mit Hilfe der Gamma-Funktion und der Mellin-Transformation von ist daher zentral, da sie ein Ausgangspunkt für die analytische Fortsetzung der Zeta-Funktion ist. Außerdem können mit ihr charakteristische Funktionalgleichungen und die Beziehung zur Theorie der Modulformen hergeleitet werden.
Methoden zur analytischen Fortsetzung
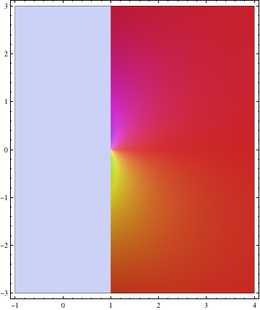
−1 < Re(s) < 4 und −3 < Im(s) < 3 mit Kolorierung der Funktionswerte: Dirichlet-Reihe, Euler-Produkt und Mellin-Transformation konvergieren nur auf der um 1 verschobenen rechten Halbebene. Sie können die Zeta-Funktion im grau gefärbten Bereich nicht darstellen.

Die anfänglich nur für komplexe Zahlen definierte Zeta-Funktion kann zu einer in ganz holomorphen Funktion ausgeweitet werden. Diese Tatsache mag zunächst ungewöhnlich wirken, da ihre Dirichlet-Reihe an vielen Stellen nicht mehr konvergiert. Tatsächlich aber steht die Dirichlet-Reihe (wie auch Euler-Produkt und Mellin-Transformation aus Gründen der Äquivalenz) nicht überall für die Definition der Zeta-Funktion zur Verfügung.
An der Stelle besitzt die Zeta-Funktion zunächst mit Sicherheit eine Definitionslücke, denn mit der Divergenz der harmonischen Reihe folgt
Also wird sie in jedem Intervall beliebig anwachsen. Diese Lücke bildet gleichzeitig eine natürliche Barriere für die Konvergenz der Dirichlet-Reihe, was aus den Regeln für Abszissen von Dirichlet-Reihen folgt, denn die betrachtete Dirichlet-Reihe hat Konvergenzabszisse .
Eine analytische Fortsetzung der im Gebiet durch die Reihe definierten holomorphen Funktion ist eine auf einem größeren Gebiet holomorphe Funktion, die auf ganz mit dieser übereinstimmt. Nach dem Identitätssatz für holomorphe Funktionen ist eine solche Fortsetzung stets eindeutig bestimmt. Damit sind alle Werte der Zeta-Funktion im erweiterten Bereich bereits durch die Dirichlet-Reihe festgelegt, obwohl sie hier nicht mehr an allen Stellen konvergiert.
Umformungen der Dirichlet-Reihe und die Eulersche Reihentransformation
Obwohl es für den ganz allgemeinen Fall kein konstruktives Verfahren gibt, Berechnungsformeln für analytische Fortsetzungen anzugeben, ist es durch die Einfachheit der Dirichlet-Reihe nicht schwierig, für die Zeta-Funktion eine zu finden. Besonders einfach erweist sich dies für die gelochte Halbebene
mittels folgender Beobachtung:[19]
Die Reihe zur Rechten konvergiert nachweislich in der Halbebene gegen eine holomorphe Funktion und wird in der Literatur auch manchmal als Dirichletsche Etafunktion bezeichnet. Damit lässt sich die Zeta-Funktion zu einer in ganz holomorphen Funktion fortsetzen. Die Lücke in wird mittels des Faktors gehoben und muss daher ein Pol erster Ordnung sein. Das Residuum der Zeta-Funktion ist dort 1, das heißt, es gilt:[20]
Alle Stellen mit sind hingegen hebbare Singularitäten, denn es gilt dann Dies zeigt man am besten mittels partieller Summation: Für alle gilt[21]
Für eine weitere holomorphe Ausdehnung des Definitionsbereiches eignen sich nun viele Methoden, die jedoch nach dem Identitätssatz alle dieselbe Funktion darstellen. Eine davon bietet die Anwendung der Eulerschen Reihentransformation auf die obere alternierende Reihe. Man erhält damit eine von Konrad Knopp veröffentlichte und auf ganz definierte Reihenidentität
Diese wurde 1930 von Helmut Hasse bewiesen.[22] Es treten daher während der weiteren Fortsetzung keine weiteren Lücken bzw. Pole mehr auf. Daraus folgt schließlich Holomorphie in .
Durch Limitierungsverfahren
Die Idee der Theorie der Limitierungsverfahren ist es, einem divergenten Grenzprozess einen endlichen Wert zuzuordnen, indem man etwa zusätzliche Parameter einführt, die man anschließend gegen den Ursprungsausdruck „limitiert“. Dies geht bereits auf Leonhard Euler zurück, der berühmt für seinen sorglosen Umgang mit divergenten Reihen ist. Er berechnete einige Werte der Zeta-Funktion annähernd auch außerhalb des Bereichs, in welchem die Dirichlet-Reihe konvergiert. Auf diese Weise stieß er auch auf seine Vermutung hinsichtlich der Gültigkeit ihrer Funktionalgleichung, die er allerdings nicht beweisen konnte.
Der Gedanke ist, der für divergenten Reihe
für alle Werte einen „Grenzwert“ zuzuordnen. Dies gelingt durch Einführen eines weiteren Parameters . Es ist die Reihe
für jedes für alle konvergent. Auf dieser Basis kann der Konvergenzbegriff abgeschwächt werden: Eine Reihe heißt A-summierbar, falls die zugehörige Potenzreihe für alle konvergiert und der Grenzwert existiert.[23] Ist eine Reihe bereits im klassischen Sinne konvergent, stimmen die jeweiligen Grenzwerte nach dem Abelschen Grenzwertsatz überein, doch es gibt A-summierbare Reihen, die nicht konvergieren. Es ist also A-Summierbarkeit eine wohldefinierte Verallgemeinerung der klassischen Reihenkonvergenz. Durch Bilden des Grenzwertes , d. h., nähert sich von links, erhält man
sogar für alle , und die rechte Seite stellt eine ganze Funktion dar.[24]

Durch die Hinzunahme einer zweiten zu limitierenden Variable entsteht zugleich eine Beziehung zum Polylogarithmus. Dieser verallgemeinert unter anderen den natürlichen Logarithmus und ist für gegeben durch die Potenzreihe
Ist zudem , so ist diese Reihe auch an den Randwerten (außer bei ) konvergent. Generell ist für feste Werte eine analytische Fortsetzung in auf das Gebiet möglich. Es gilt für alle die Beziehung , aber auch
für Werte . Etwa für gilt zunächst für (siehe Bild rechts), also nach Grenzwertbildung
Die Euler-Maclaurin-Summenformel
Eine weitere Möglichkeit, eine analytische Fortsetzung anzugeben, bietet die Euler-Maclaurin-Summenformel. Diese drückt diskrete Summen explizit in der Sprache der Integralrechnung aus und ist allgemein gegeben durch
Hierbei ist eine auf dem Intervall mindestens -mal differenzierbare Funktion und eine natürliche Zahl. Es bezeichnen zudem die Bernoulli-Polynome und den ganzzahligen Anteil von .[25]
Mit , und folgt also[26]
Dabei ist das Restglied gegeben durch[26]
und konvergiert in der gesamten Halbebene (gleichmäßig auf kompakten Teilmengen). Daher stellt diese Formel eine holomorphe Fortsetzung der Zeta-Funktion in die Halbebene dar. Lässt man gegen unendlich gehen, ergibt sich damit ein holomorpher Ausdruck für ganz .[27]
Setzt man zum Beispiel , ergibt sich die in der Literatur häufig zitierte Darstellung
die für gültig ist.[28]

Integration über eine Hankel-Kontur
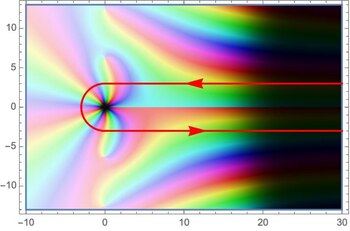
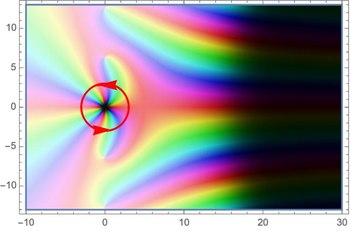
Eng verwandt mit der Darstellung der Zeta-Funktion mittels der Mellin-Transformation ist eine Darstellung der Funktion mittels eines Kurvenintegrals. Diese wurde von Riemann selbst verwendet, um die Zeta-Funktion in die komplexe Ebene fortzusetzen. Die Funktion ist je nach Wahl des Zweiges des Logarithmus in unterschiedlichen Bereichen holomorph. Für die Hankel-Kontur (einen speziellen Integrationsweg) ist es von Vorteil, die Gerade aus dem Gebiet auszuschließen via:
Nun definiert man für die Funktion als ein Kurvenintegral über . Die gewählte Kurve kommt von , verläuft mit Abstand über der reellen Geraden, umläuft den Ursprung in einem Halbkreis und erstreckt sich dann wieder mit Abstand unterhalb der reellen Geraden gegen :
Wegen gleichmäßiger Konvergenz auf kompakten Mengen in ist eine ganze Funktion. Wählt man nun , so kann man wegen die Schlaufe beliebig zusammenziehen und erhält mit der Mellin-Transformation
Daraus ergibt sich mit dem Ergänzungssatz die Formel[29]
Ist , so ist innerhalb des gelochten Streifens holomorph. Damit lässt sich die Hankel-Kontur zu einer Kreiskurve zusammenziehen, ohne den Wert des Integrals zu verändern. Dies ermöglicht eine schnelle Berechnung der Werte für ganze Zahlen mittels des Residuensatzes. Unter anderem folgt daraus
für alle und die enge Beziehung der Werte der Zeta-Funktion an nicht-positiven ganzen Argumenten und den Bernoulli-Zahlen.
Diese Darstellungsform kann auch zu einer direkten Herleitung der Funktionalgleichung verwendet werden. Dabei wird die Kurve modifiziert und es kommt der Residuensatz zum Einsatz.[30]
Weitere Darstellungsmöglichkeiten
Erwähnenswert ist der Reihenausdruck
- ,
der für alle Werte definiert ist.[31] Interessant daran ist, dass sich damit die Zeta-Funktion rekursiv auf die ganze Zahlenebene fortsetzen lässt, da für die Berechnung von lediglich die Werte benötigt werden.
Von Helmut Hasse stammt die global konvergente Reihe[32]
Ein exotischer und global konvergenter Ausdruck ergibt sich, wenn man direkt die elementare Reihendarstellung der Zeta-Funktion in die Abel-Plana-Summenformel einsetzt:[33]
Geschichte
Im Gegensatz zu den Primzahlen oder der euklidischen Geometrie ist die mathematische Entdeckungsgeschichte der Riemannschen Zeta-Funktion sehr jung. So sind alle bis heute wesentlichen Entdeckungen zu dieser Funktion in den letzten 250 Jahren gemacht worden. Auf der einen Seite lässt sich die im Verhältnis zur Entstehung einer rigorosen (komplexen) Analysis frühe Entdeckung mit der Einfachheit der Reihe begründen. Auf der anderen Seite lassen sich die späten Resultate mit der Schwierigkeit von deren Eigenschaften erklären.
Um 1735 löste Leonhard Euler das Basler Problem


Einer der ersten Mathematiker, der sich mit einem Vorläufer der wie heute definierten Zeta-Funktion intensiv und ausführlich auseinandersetzte, war Leonhard Euler. Seit Mitte des 17. Jahrhunderts versuchten Mathematiker, den exakten Grenzwert der unendlichen Reihe
zu bestimmen. Persönlichkeiten wie Pietro Mengoli, der das Basler Problem (wie es später bezeichnet wurde) erstmals formulierte, aber auch Jakob I Bernoulli scheiterten mit ihren Lösungsversuchen. Erst um das Jahr 1734 fand Leonhard Euler die Lösung
mit der Kreiszahl , indem er eine neuartige Technik zur Berechnung der Sinusfunktion entwickelte.[34] Dieser Beweis wurde jedoch nach Veröffentlichung von seinen Zeitgenossen zunächst nicht akzeptiert. Daraufhin konterte er mit der Veröffentlichung eines alternativen Beweises im Jahr 1741.[35] Natürlicherweise war Euler bald darauf an der Untersuchung von Reihen des Typs
interessiert. Er hatte die Hoffnung, weitere und außerdem weit bedeutendere Aussagen treffen zu können. Und tatsächlich sollte es nicht nur bei der Lösung des Basler Problems bleiben. Er fand unter anderem die Formeln
die 1735 in seiner Arbeit De Summis Serierum Reciprocarum erstmals veröffentlicht wurden. Obwohl mit steigenden Eingabezahlen die Funktionswerte komplizierter werden, berechnete Euler von Hand[36] den Wert
In seinem Buch Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum, das 1755 veröffentlicht wurde, bewies er schließlich eine allgemeine Formel für .[37] Diese zeigte auf, dass sich tatsächlich jedes stets als ein rationales Vielfaches der Potenz schreiben lässt. Nicht erfolgreich war er hingegen bei ungeraden Argumenten, also zum Beispiel bei der Reihe
da sich hier keine seiner Techniken anwenden ließ. Jedoch berechnete er die Werte für bis auf mehrere Dezimalstellen. Außerdem schrieb er einheitlich , wobei im Falle, dass eine gerade Zahl ist, rational ist. Für den Fall, dass ungerade ist, vermutete Euler, sei „eine Funktion von “.[38] Dies konnte jedoch, ungeachtet der vagen Formulierung Eulers, bis heute nicht bestätigt werden. Die Werte der Reihen für ungerade Argumente größer als 1 sind bis heute (Stand 2020) weitestgehend unbekannt und Gegenstand zahlentheoretischer Vermutungen.[39]
Euler gilt als Entdecker der Verbindung zwischen der Zeta-Funktion und den Primzahlen. Diese Verknüpfung wird bis heute als Euler-Produkt bezeichnet. So schrieb er in seiner Arbeit Variae observationes circa series infinitas:
„Wenn aus der Reihe der Primzahlen der folgende Ausdruck gebildet wird wird sein Wert der Summe dieser Reihe gleich sein “
Sofort war sich Euler der Beziehung zwischen den Primzahlen und der Geometrie bewusst, und er schrieb weiter:
„Weil nach Setzen von gilt , wobei die Peripherie des Kreises bezeichnet, dessen Durchmesser 1 ist, wird sein “
Aus der schon damals gut bekannten Tatsache, dass die harmonische Reihe divergent ist, konnte Euler ebenfalls aus dem Euler-Produkt schließen, dass die Summe der Kehrwerte aller Primzahlen keinen endlichen Grenzwert hat.[42] Bezeichnet wird dieses Resultat auch als Satz von Euler über die Summation der Kehrwerte der Primzahlen.
Auch war die von Riemann später bewiesene Funktionalgleichung bereits Euler bekannt. In seiner Arbeit Remarques sur un beau rapport entre les series des puissances tant directes que reciproques beschrieb er diese mathematisch nicht rigoros:[43]
„Par cette raison je hazarderai la conjecture suivante, que quelque soit l’exposant n, cette équation ait toujours lieu:
- “
„Aus diesem Grund wage ich die folgende Vermutung vorzuschlagen, dass für jede Variable n die folgende die Gleichung immer gültig ist:
- “
Dabei bezog sich Euler eigentlich auf die Dirichletsche Etafunktion, die jedoch bis auf einen Faktor der Riemannschen Zeta-Funktion entspricht. Euler gab keinen rigorosen Beweis einer Funktionalgleichung, sondern hatte diese nur für viele Werte überprüft und anschließend als universell gültig vermutet.
Dirichlet zeigt seinen Primzahlsatz

Im Jahre 1838 gelang dem Mathematiker Peter Dirichlet ein großer Beitrag zur Zahlentheorie. Er bewies eine Vermutung von Fermat, die nun Dirichletscher Primzahlsatz heißt. Diese besagt, dass jede arithmetische Progression mit positiven, teilerfremden unendlich viele Primzahlen enthält.[45] Ist hier zum Beispiel und , folgt, dass die Liste 1, 5, 9, 13, 17 … unendlich viele Primzahlen beinhaltet.
Schlüssel zum Beweis waren neben der Riemannschen Zeta-Funktion eine ganze Klasse weiterer Funktionen, die ebenfalls in Primzahlprodukte zerfallen und somit eine „große Familie“ bilden. Erst ein Jahrhundert später konnten dank feinerer Methoden die Ergebnisse von Dirichlet durch Siegel und Walfisz deutlich präzisiert werden (Satz von Siegel-Walfisz).
Riemanns Beitrag zur Zeta-Funktion

Im Jahr 1859 arbeitete Bernhard Riemann in seiner Publikation Über die Anzahl der Primzahlen unter einer gegebenen Größe den bereits von Euler gegebenen Zusammenhang der Zeta-Funktion zu den Primzahlen entscheidend aus. Die große Leistung bestand darin, die Relevanz der Ausweitung des Definitionsbereichs auf komplexe Zahlen zu erkennen. Erst mit dieser Herangehensweise war es möglich geworden, konkrete Informationen über Primzahlen 2, 3, 5, 7 … selbst zu gewinnen. Das ist insofern bemerkenswert, als Primzahlen reelle Zahlen sind. Riemann, der ein Schüler von Carl Friedrich Gauß war, schrieb in seiner zehnseitigen Arbeit eine funktionentheoretische Interpretation und Auswertung des Euler-Produkts, die einen Zusammenhang zwischen Primzahlen und den nicht-trivialen Nullstellen der Zeta-Funktion schaffte. Das Hauptresultat war eine Formel, die ohne jeden Fehler die Anzahl der Primzahlen unter einer gegebenen (nicht ganzen) positiven Zahl abzählte. Damit war ihm ein völlig neuer Zugang zur Theorie der Primzahlen gelungen.
Er etablierte in seiner Arbeit das griechische (Zeta) als Funktionssymbol und formulierte außerdem die bis heute unbewiesene nach ihm benannte Riemannsche Vermutung, die eine wichtige Aussage über die genaue Lage der Nullstellen der Zeta-Funktion behauptet.

Obwohl der Artikel heutzutage als Durch- und Aufbruch zur modernen analytischen Theorie um die Zeta-Funktion gesehen wird, stieß er damals in Mathematikerkreisen bei Weitem nicht nur auf Begeisterung. Schuld daran war in erster Linie, dass Riemann es an den meisten Stellen unterlassen hatte, Beweise für seine aufgestellten Formeln zu hinterlegen. So kam es, dass Godfrey Harold Hardy und John Edensor Littlewood Riemanns Arbeit lediglich als „beachtliche Ansammlung heuristischer Einsichten“ bezeichneten,[46] die englischen Mathematiker waren allerdings in der analytischen Zahlentheorie zu Beginn des 20. Jahrhunderts anfangs noch so rückständig, dass Littlewood sich erinnerte, die Riemannsche Vermutung 1906 von seinem Professor als Übungsaufgabe gestellt bekommen zu haben. Auch Edmund Landau gehörte zu den lautesten Kritikern hinsichtlich der Bedeutung des Artikels. Zwar nannte er ihn zunächst „brillant und fruchtbar“, jedoch schlug sein Lob bald um:
„Riemanns Formel ist bei weitem nicht das wichtigste in der Theorie der Primzahlen. Er schuf einige Hilfsmittel, die, wenn sie erstmal ausgearbeitet sind, manche anderen Beweise ermöglichen werden.“
Detlef Laugwitz bemerkt dazu in seiner Riemann-Biographie, dass Landau auch Eulers bahnbrechende Arbeiten in seinen Lehrbüchern wenig würdigte, da er tendenziell nur Arbeiten schätzte, in denen jedes Detail ausgearbeitet war.[48] Auf der anderen Seite bewunderten Mathematiker wie Felix Klein, Riemann habe „mit großen allgemeinen Ideen“ gearbeitet und „oft auf seine Intuition“ vertraut.[49] Das war noch bevor Carl Ludwig Siegel durch das Studium des Nachlasses zeigte, wie umfangreich Riemanns analytische Arbeiten zur Zeta-Funktion waren. Die Rechnungen im Nachlass waren allerdings schwer zu entschlüsseln und es bedurfte eines Mathematikers vom Kaliber Siegels, die Ideen Riemanns zu rekonstruieren.
Riemann arbeitete seit dieser Zeit bis zu seinem frühen Tode (er starb mit gerade mal 39 Jahren an den Folgen einer Tuberkulose) nicht mehr an der Zeta-Funktion, es blieb seine einzige Veröffentlichung zur Zahlentheorie.[50] Der Aufsatz von 1859 war nur skizzenhaft ausgeführt, Riemann wollte sich damit für die Aufnahme in die Berliner Akademie der Wissenschaften bedanken.
Viele von Riemanns Aufzeichnungen wurden nach seinem Ableben von seiner Haushälterin verbrannt, bis sie von Mitarbeitern der Göttinger Fakultät gestoppt wurde. Die verbliebenen Schriften wurden seiner Witwe übergeben und verschwanden damit für viele Jahre. Über weitere Resultate zur Zeta-Funktion, die man ohne teilweise Vernichtung der Dokumente gefunden hätte, kann bis heute nur noch spekuliert werden.
Die letzten Jahre des 19. Jahrhunderts
Mangoldt beweist die Hauptformel von Riemann
Im Jahr 1893 publizierte der Mathematiker Jacques Hadamard eine Arbeit, in welcher der Grundstein eines detaillierteren Verständnisses von Riemanns Arbeit gelegt wurde. Hadamard war es gelungen, eine Formel für die Zeta-Funktion zu beweisen, die ihre Nullstellen beinhaltet. Genau genommen handelte es sich dabei um ein Verfahren, die Zeta-Funktion als Ganzes aus ihren Nullstellen zu konstruieren. Die Existenz einer solchen Formel wurde von Riemann bereits vorausgesetzt, war jedoch bis dato nicht rigoros bewiesen worden. Für die Verifikation der Riemannschen Ideen war sie aber ein substanzieller Teil: das Grundschema der Argumentation für Riemanns Hauptformel lautete nämlich „Primzahlprodukt (Euler) versus Nullstellenprodukt (Riemann/Hadamard)“. Unter anderem deshalb bezeichnete Hans von Mangoldt den Beitrag von Hadamard „als ersten wirklichen Fortschritt in diesem Gebiet seit 34 Jahren“.[51][52]
Aufbauend auf der Arbeit von Hadamard gelang Hans von Mangoldt nur zwei Jahre später, im Jahre 1895, der Durchbruch zu Riemanns Hauptformel.[53] Allerdings zeigte er diese in einer leicht veränderten Version, die heute als „natürlicher“[54] angesehen wird. Seiner Leistung zu Ehren wird die Hauptformel heute als Riemann-von-Mangoldt-Formel bezeichnet.
Hadamard und De La Vallee-Poussin beweisen den Primzahlsatz
Nachdem von Mangoldt im Jahr 1895 den Beweis der Riemannschen Hauptformel erbracht hatte, fehlte zum Beweis des Primzahlsatzes nicht mehr viel. Dieser Satz trifft eine Aussage darüber, wie häufig Primzahlen durchschnittlich auftauchen. Es blieb lediglich zu zeigen, dass die Zeta-Funktion keine Nullstellen in dem Bereich hat, in dem das Primzahlprodukt von Euler „gerade so nicht mehr gültig ist“. Unabhängig voneinander erbrachten Hadamard und der Belgier Charles-Jean de La Vallée Poussin den Beweis im Jahr 1896.[55] Wichtige Punkte für den Beweis waren Ideen von Franz Mertens und die trigonometrische Identität .[56]
Obwohl die Aufregung in der Mathematikerwelt groß war, gab es bezüglich der Beweismethode, die stark an die Eigenschaften der schwierigen Zeta-Funktion gebunden war, Bedenken über deren Natürlichkeit. Es wurde als seltsam erachtet, dass eine Aussage über Primzahlen sogar äquivalent zu einer gewissen Verteilung der Nullstellen einer komplexen Funktion war. So äußerte Albert Ingham 1932:
„Man kann den Beweis des Primzahlsatzes, […] von de la Vallée Poussin und Hadamard für unbefriedigend halten, denn es werden Begriffe eingeführt, die sehr weit vom ursprünglichen Problem entfernt sind. Deswegen ist es nur allzu natürlich, nach einem Beweis zu fragen, der nicht von der Theorie der Funktionen einer komplexen Veränderlichen abhängt. Hierauf müssen wir antworten, daß gegenwärtig kein derartiger Beweis bekannt ist. Wir können in der Tat weiter gehen und sagen, daß es unwahrscheinlich ist, dass ein wahrhaft reeller Beweis gefunden wird; zumindest ist das so lange unwahrscheinlich, wie sich die Theorie auf die Eulersche Identität stützt. Denn jeder bekannte Beweis des Primzahlsatzes stützt sich auf eine gewisse Eigenschaft der komplexen Nullstellen von und umgekehrt ist diese Eigenschaft eine einfache Folgerung des Primzahlsatzes selbst. Es scheint deswegen klar zu sein, daß diese Eigenschaft explizit oder implizit in jedem Beweis verwendet werden muss, der auf beruht, und man erkennt nicht, wie ein Beweis geführt werden soll, wenn man lediglich die reellen Werte von verwendet.“
Im Jahr 1948 wurde schließlich ein elementarer (also gänzlich ohne funktionentheoretische Mittel auskommender) Beweis von Atle Selberg und Paul Erdös gegeben.[59] Hierbei bedeutet „elementar“ jedoch keinesfalls „einfach“.[60] Es wurden im Lauf der Zeit auch erheblich einfachere funktionentheoretische und elementare[61] Beweise des Primzahlsatzes gefunden.
Anfang des 20. Jahrhunderts
Hilbert formuliert seine 23 Probleme

Im Rahmen des 2. Internationalen Mathematikerkongresses des Jahres 1900 in Paris hielt David Hilbert am 8. August einen Vortrag. In diesem formulierte er eine Liste von 23 mathematischen Problemen, die seiner Ansicht nach zu den wichtigsten des kommenden Jahrhunderts zählten. Hilbert zählte zu diesem Zeitpunkt bereits zu den führenden Mathematikern der Gegenwart. Problem Nr. 8 war die Riemannsche Vermutung:
„In der Theorie der Verteilung der Primzahlen sind in neuerer Zeit durch Hadamard, De La Vallee-Poussin, V. Mangoldt und andere wesentliche Fortschritte gemacht worden. Zur vollständigen Lösung der Probleme, die uns die Riemannsche Abhandlung "Über die Anzahl der Primzahlen unter einer gegebenen Größe" gestellt hat, ist es jedoch noch nötig, die Richtigkeit der äußerst wichtigen Behauptung von Riemann nachzuweisen, daß die Nullstellen der Funktion , die durch die Reihe dargestellt wird, sämtliche den reellen Bestandteil haben – wenn man von den bekannten negativ ganzzahligen Nullstellen absieht. Sobald dieser Nachweis gelungen ist, so würde die weitere Aufgabe darin bestehen, die Riemannsche unendliche Reihe für die Anzahl der Primzahlen genauer zu prüfen und insbesondere zu entscheiden, ob die Differenz zwischen der Anzahl der Primzahlen unterhalb einer Größe und dem Integrallogarithmus von in der Tat von nicht höherer als der ten Ordnung in unendlich wird, und ferner, ob dann die von den ersten komplexen Nullstellen der Funktion abhängenden Glieder der Riemannschen Formel wirklich die stellenweise Verdichtung der Primzahlen bedingen, welche man bei den Zählungen der Primzahlen bemerkt hat.“
Das hohe Ansehen, das Hilbert genoss, beflügelte die Mathematiker, sich mit seinen Problemen, darunter der Zeta-Funktion, auseinanderzusetzen. Bis heute gelten 15 der 23 Probleme als gelöst, jedoch nicht die Riemannsche Vermutung.[63]
Ramanujans Arbeit zur Zeta-Funktion


Im Jahre 1910 veröffentlichte der indische Mathematiker Srinivasa Ramanujan im Journal of the Indian Mathematical Society einen Artikel, in dem unter anderem die folgende Gleichung behauptet wurde:
Die meisten Mathematiker, die diese Gleichung zu Gesicht bekamen, hatten sie als offensichtlichen Schwachsinn gewertet. So kam es, dass Professor Hill vom University College in London schrieb:
„Mr. Ramanujan ist ein Opfer der Fallstricke des sehr schwierigen Gebietes der divergenten Reihen geworden.“
Hill verhielt sich jedoch nicht völlig ablehnend und ermutigte Ramanujan, es weiter zu versuchen. Und so schickte dieser seine Ergebnisse direkt an einige Mathematiker in Cambridge. Zwei davon waren nicht in der Lage, die Aussagen hinter Ramanujans verschlüsselten Formeln zu erkennen, und lehnten die Bitte um Unterstützung ab. Als Ramanujan jedoch schließlich auch Godfrey Harold Hardy brieflich auf seine Ideen aufmerksam machte, wurde diesem in der Gleichung die korrekte Auswertung des Werts bewusst, auch wenn sie bezüglich ihrer mathematischen Formalität natürlich inkorrekt war. In diesem Zusammenhang war die Formel schon Euler bekannt, da sie sich aus und der Funktionalgleichung ergibt (beides von Euler gefunden). Ferner erweckte Ramanujans Behauptung, eine Formel zu besitzen, die fast fehlerfrei voraussage, ob eine gegebene Zahl prim sei oder nicht (Ramanujans Formel verwendete jedoch nicht die Nullstellen der Zeta-Funktion[64]), viel Neugier. Auch in einem zweiten Brief gab er jedoch dazu keinen Beweis. Littlewood äußerte:
„Dieser Brief konnte einen rasend machen.“
Der anfänglich ausschließlich schriftliche Austausch gipfelte schließlich in einem Aufenthalt Ramanujans in England, wo sich das Duo aus Ramanujan und Hardy zu einer der produktivsten und außergewöhnlichsten mathematischen Korrespondenzen der Geschichte entwickelte.[66]
Unter anderem nach Auswertung der Tagebücher Ramanujans durch George E. Andrews und Bruce Berndt offenbarten sich die zahlreichen Ideen Ramanujans zur Riemannschen Zeta-Funktion. So fand dieser unabhängig Eulers Formel für ,[67] das Euler-Produkt[68] sowie zahlreiche unendliche Reihen und Integrale, die Zeta-Werte an ganzen und auch halbzahligen[69] Stellen beinhalten.[70][71][72]
Der Nachlass Riemanns

Fünfzig Jahre nach Riemanns Tod tauchten einige nicht verbrannte Seiten wieder auf. Richard Dedekind, ein Kollege von Riemann hatte einige Seiten des Nachlasses von Riemanns Frau Elise erhalten und einige davon in der Bibliothek von Göttingen hinterlegt. Nachdem der Mathematikhistoriker Erich Bessel-Hagen 1926[73] die Schriften fand und beim Versuch einer Entschlüsselung der wirren Aufzeichnungen keinen Erfolg hatte, gingen die Dokumente an Carl Ludwig Siegel. Dieser war erstaunt von der Tiefe der Gedanken Riemanns bezüglich der Zeta-Funktion.[74] Dies entkräftete zugleich viel Kritik an Riemanns Originalarbeit, da die Notizen zeigten, dass Riemanns Behauptungen auf gründlichen Rechnungen beruhten.[75] Jedoch beklagte auch Siegel das Chaos in den Notizen:
„Nichts von dem, was Riemann über die Zeta-Funktion aufgeschrieben hatte, war reif für eine Veröffentlichung. Manchmal findet man unzusammenhängende Formeln auf derselben Seite, oft nur die Hälfte einer Gleichung.“
Siegel kam dahinter, dass Riemann ausschließlich über handschriftliche Rechnungen mindestens drei nicht-triviale Nullstellen der Zeta-Funktion relativ genau berechnet hatte. Die dafür verwendete Formel wurde durch Siegel ausgearbeitet, 1932 publiziert und wird seitdem auch Riemann-Siegel-Formel genannt.[77]
Nach 1945 bis heute
Im Zeitalter des Computers
In der Forschung rund um die Riemannsche Zeta-Funktion werden Computer vor allem dazu benutzt, die Korrektheit der Riemannschen Vermutung für möglichst viele Nullstellen zu überprüfen. Obwohl es sich bei allen Rechnungen um numerische Verfahren handelt, zeigen diese exakt und nicht nur annähernd, dass sich die untersuchten Nullstellen auf der kritischen Geraden befinden.[78][79]
Bereits im Jahr 1936 hatte der in Oxford wirkende Mathematiker Edward Charles Titchmarsh mit einer Maschine, die ursprünglich für astronomische Berechnungen konstruiert worden war, die ersten 1.041 nicht-trivialen Nullstellen der Zeta-Funktion berechnet.[80] Im Jahr 1953 wurden diese Berechnungen von Alan Turing fortgesetzt. Seine Methode wird bis heute benutzt. Erstmals kam dabei ein Computer zum Einsatz.[81][82]
Ab Beginn der 80er Jahre wurden die Computer immer leistungsstärker. Bereits im Jahr 1979 hatte eine Gruppe aus Amsterdam um Herman te Riele und Richard P. Brent 200 Millionen Nullstellen überprüft (etwas später erhöhten sie ihre Rechnung auf 300 Millionen) – alle lagen auf der kritischen Geraden. Damit widersprachen sie einer Vorhersage von Don Zagier, der geäußert hatte, es sei „ein Wunder“, falls diese immer noch ausnahmslos auf der kritischen Geraden lägen.[83] Zagier berief sich dabei auf theoretische Gründe, die zwar die Lage der ersten paar Tausend Nullstellen auf der Geraden bekräftigten, jedoch für steigende Zahlen schwächer – und letztlich sogar dagegen sprechend – auszulegen waren.
Bis 2005 wurden im Rahmen des sog. ZetaGrid Project durch verteilte Rechner die ersten 900 Milliarden Nullstellen überprüft. Um dieselbe Zeit berechnete Xavier Gourdon mit Unterstützung von Patrick Demichel die ersten 10 Billionen () Nullstellen.[84][85] Alle lagen auf der kritischen Geraden.
Zahlentheorie trifft Quantenphysik


Im Jahr 1972 offenbarte sich durch ein zufälliges Gespräch zwischen dem Physiker Freeman Dyson und dem Mathematiker Hugh Montgomery ein bis dahin unbemerkter Zusammenhang zwischen Quantenphysik und Zahlentheorie. Gegenstand der Diskussion waren die Nullstellen der Riemannschen Zeta-Funktion. In deren von Montgomery vermuteten Verteilung erkannte Dyson die Abstände zwischen Paaren von Eigenwerten von Hermitschen Zufallsmatrizen wieder. Diese werden von Quantenphysikern zur Vorhersage der Energieniveaus in einem schweren Atomkern verwendet, wenn dieser mit nieder-energetischen Neutronen bestrahlt wird. Als Montgomery sich die Abstände zwischen den Energieniveaus in dem Atomkern Erbium, dem 68. Element im Periodensystem, anschaute, erkannte er eine auffallende Ähnlichkeit. Die allgemeine Übereinstimmung zwischen einem gewissen Ausschnitt der Nullstellenorte auf der kritischen Geraden und den experimentell bestimmten Energieniveaus zeugte von großer Signifikanz.[87]
Durch umfassenden Einsatz von Computern wurde die Vermutung von Montgomery über die Nullstellenabstände von Andrew Odlyzko überprüft. Die Zahlen sprachen dabei für Montgomerys Annahme. 1987 publizierte Odlyzko seine Ergebnisse.[88]
Trotz starker Evidenzen wurden die Ergebnisse teilweise skeptisch gesehen. Es kam die Frage auf, ob damit irgendwelche Fortschritte in der reinen Mathematik erzielt worden waren. So äußerte der Zahlentheoretiker Peter Sarnak aus Princeton:
„Es ist ja recht faszinierend, die gleichen Bilder in beiden Gebieten zu sehen, doch wer kann einen wirklichen Beitrag zur Zahlentheorie nennen, der dadurch erst möglich geworden ist?“
Jonathan Keating, ein Schüler des Physikers Michael Berry, lieferte schon bald eine zahlentheoretische Anwendung. Berry hatte sich zuvor schon mit Zusammenhängen zwischen Primzahlen und Quantenphysik beschäftigt (insbesondere Verbindungen zum Quantenchaos). Doch es waren schließlich Keating und seine Doktorandin Nina Snaith, die mit Hilfe statistischer Methoden (die häufig in der Quantenphysik zum Einsatz kommen) eine exakte Formel für das durchschnittliche Verhalten von Potenzen der Absolutwerte der Zeta-Funktion entlang der kritischen Geraden aufstellten. Diese Durchschnittswerte sind für die Zahlentheorie von Bedeutung und haben viele Anwendungen, zum Beispiel auf das Dirichletsche Teilerproblem. Wenige Minuten vor Keatings Vorstellung der Ergebnisse hatte er zusammen mit Snaith die Formel an einer Tafel „getestet“, indem sie schauten, ob ein bereits mühsam erarbeitetes Ergebnis korrekt vorausgesagt würde. Das Besondere an der Herangehensweise von Keating und Snaith, die unter anderem von Atle Selberg gelobt wurde[90], war, dass sie Primzahlen dabei als Zufallsvariablen, also gewissermaßen Resultate eines Münzwurfes interpretierten. Sarnak lenkte ein und gestand zu, dass ohne diesen fremdartigen Ansatz eine solche Vermutung über die Zeta-Funktion nicht hätte erarbeitet werden können.[91]
Montgomerys Paar-Korrelation-Vermutung und das asymptotische Verhalten der Zeta-Momente sind bis heute Gegenstand intensiver Forschung.
Die Riemannsche Vermutung bis heute
Spätestens nachdem Hilbert die Riemannsche Vermutung auf die Liste seiner Probleme genommen hatte, erweckte sie das Interesse zahlreicher Mathematiker. Doch bis heute erweist sich das Problem als außerordentlich schwierig.
Nachdem 1942 Atle Selberg gezeigt hatte, dass ein positiver Anteil der Nullstellen auf der kritischen Geraden liegen muss, entwickelte sich daraus ein wahrer Wettlauf um die Größe dieses Anteils. Norman Levinson zeigte, dass gut ein Drittel die Vermutung erfüllen, und Brian Conrey zeigte 1989, dass es sogar gut 40 Prozent sind. Ob diese Methoden aber letztlich zu einer Lösung führen, gilt als umstritten. Nicht mal ein solcher Beweis, dass „100 Prozent“ (in einem asymptotischen Sinn) der Nullstellen der Vermutung gehorchen, wäre zwingend zielführend, da die Anzahl der Nullstellen unendlich groß ist. Ähnliche Bedenken existieren gegenüber den unternommenen Anstrengungen, nullstellenfreie Regionen zu optimieren.
Stephen Smale, Träger der Fields-Medaille, veröffentlichte 1998 seine eigene – im Sinne von Hilbert verfasste – Liste von 18 Problemen. Problem Nummer 1 ist die Riemannsche Vermutung. Bisher wurden nur wenige Probleme auf Smales Liste gelöst (siehe Smale-Probleme).
Weitere Berühmtheit erlangte die Riemannsche Vermutung, als sie im Jahr 2000 vom Clay Mathematics Institute (CMI) auf die Liste der Millennium-Probleme gesetzt wurde.[92] Für einen schlüssigen Beweis ist damit ein Preisgeld von 1 Million US-Dollar ausgelobt.
Praktische Anwendungsgebiete
Es werden im Folgenden Anwendungen mit praktischem Bezug gegeben. Beziehungen zur mathematischen und physikalischen Grundlagenforschung finden sich weiter unten in den Bereichen:
- Analytische Zahlentheorie
- Algebraische Zahlentheorie und Geometrie
- Automorphe Formen
- Wahrscheinlichkeitstheorie und Statistik
Schnelle Primzahltests
Ein Primzahltest ist ein Algorithmus, der überprüft, ob eine gegebene Zahl eine Primzahl ist. Verfährt man hier völlig naiv, muss dafür nachgerechnet werden, ob eine der Zahlen mit ein Teiler von ist. Teilt keine dieser Zahlen , so muss es eine Primzahl sein, da jeder Teiler größer als zu einem Teiler kleiner als korrespondiert über . Dieses Verfahren erfordert ca. Rechenoperationen, da ungefähr Quotienten gebildet und ausgewertet werden müssen. Damit wird es, trotz seiner Einfachheit, als aufwändig erachtet.
Die Lage der Nullstellen der Riemannschen Zeta-Funktion spielt eine Rolle beim Beweis der Existenz schnellerer Primzahltests. Unter der Annahme der Verallgemeinerten Riemannschen Vermutung konnte Gary L. Miller 1976 zeigen, dass es einen deterministischen Primzahltest gibt, der in Schritten (d. h. „schnell“) prüft, ob eine Primzahl ist oder nicht.[93] Der Begriff Verallgemeinerte Riemannsche Vermutung bedeutet, dass nicht nur die Riemannsche Zeta-Funktion, sondern auch sämtliche Dirichletschen L-Funktionen niemals für Argumente mit den Wert Null annehmen.
1980 gelang es Michael O. Rabin diesen zu einem probabilistischen Test umzuwandeln, der zwar niemals ein Ergebnis zu 100 Prozent korrekt ausgibt, jedoch nach hinreichend vielen Schritten sehr zuverlässig ist. Dieser funktioniert unabhängig von der Riemannschen Vermutung.[94]
Große Primzahlen werden bei der Verschlüsselung von Daten (zum Beispiel im Internet) verwendet. Die Sicherheit solcher Systeme beruht auf der Annahme, dass es kein schnelles Verfahren gibt, eine Zahl in ihre Primfaktoren zu zerlegen. Beim RSA-Kryptosystem nimmt eine Person, die eine Nachricht verschlüsseln möchte, zwei große Primzahlen und mit großem Abstand zueinander, und bildet die zusammengesetzte Zahl . Mit Hilfe dieser können nun Nachrichten (wenn zuvor in Zahlen umgewandelt) durch einen öffentlichen Schlüssel, der aus und erzeugt wurde, verschlüsselt werden. Dieser Schlüssel steht jedermann zur Verfügung, gibt jedoch keine Einsicht in das Kryptosystem an sich. Mit dem Wissen um und kann eine Nachricht aus der Öffentlichkeit an den Privatmenschen anschließend wieder entschlüsselt werden, da mit dem Wissen um und auch der „Gegenschlüssel“ erzeugt werden kann, der den Klartext wieder herstellt. Dieser Gegenschlüssel steht nur der Privatperson zur Verfügung und ist daher ein privater Schlüssel. Zum Brechen des Systems ist folglich die Faktorisierung von erforderlich.
Physik
In der Physik spielt die Riemannsche Zeta-Funktion eine vielseitige Rolle. Anwendungen haben etwa spezielle Funktionswerte:[95]
- Der Wert wird u. a. bei der Berechnung der kritischen Temperatur für die Ausbildung eines sogenannten Bose-Einstein-Kondensats und in der Spinwellen-Theorie bei magnetischen Systemen benötigt.
- Der Wert wird im Hochtemperatur-Limes in der Zustandsdichte für den harmonischen Oszillator gebraucht.
- Der Wert wird in der Zustandsdichte für ein freies Bosonengas benutzt.
- Die Konstante steht im Zusammenhang mit dem Integral über die Strahlungsdichte der Planckschen Schwarzkörperstrahlung.
Regularisierung von Determinanten
Zeta-Funktionen sind eine Möglichkeit zur Regularisierung von Funktionaldeterminanten von Operatoren auf unendlich-dimensionalen Räumen, der Vorgang nennt man Zetafunktions-Regularisierung. Solche Regularisierungen haben Anwendungen in der Physik, zum Beispiel in der Quantenfeldtheorie und in der String-Theorie.[96] Dabei werden, ähnlich wie es bereits Ramanujan tat, divergenten Reihen endliche Werte zugeordnet. Ein Anwendungsbeispiel einer solchen Regularisierung betrifft den Casimir-Effekt.[97]
Die Formel von Ramanujan und Euler für kann heuristisch dazu dienen, auf einfache Weise die Notwendigkeit von 26 Raum-Zeit-Dimensionen in der bosonischen Stringtheorie abzuleiten.[98]
Das Zipfsche Gesetz
Das Zipfsche Gesetz wurde ursprünglich in der quantitativen Linguistik formuliert und besagt, dass bei einem Korpus von natürlichsprachlichen Äußerungen die Häufigkeit eines Wortes umgekehrt proportional zu seinem Rang in der Häufigkeitstabelle ist.[99] So wird das häufigste Wort etwa doppelt so oft vorkommen wie das zweithäufigste Wort, dreimal so oft wie das dritthäufigste Wort usw. Bei der Verwendung von verschiedenen Wörtern hat dies eine Wahrscheinlichkeitsverteilung von
mit der harmonischen Folge zur Konsequenz. Je nach Art des Datensatzes kann es aber sein, dass ein anderer Exponent gebraucht wird. Mit der verallgemeinerten harmonischen Folge lässt sich für reelle Parameter die verallgemeinerte Verteilung
beschreiben. Im Falle von lässt sich damit die für „unendlich viele Wörter“ geeignete Zeta-Verteilung erzeugen:[100]
Globale Eigenschaften
Funktionalgleichung

Im Folgenden bezeichnet die Gammafunktion, die die Fakultät auf komplexe Zahlen verallgemeinert. Auf ganz gilt als Identität zwischen meromorphen Funktionen[101]
Aus dieser geht durch einfache Umformung die alternative Darstellung
für alle hervor. Oft wird auch die symmetrische Variante der Funktionalgleichung, nämlich
in der Literatur zitiert. Man beachte die Invarianz, die unter der Variablentransformation entsteht.[102][103][104] Aus der symmetrischen Variante können die oberen Gleichungen mittels der Legendreschen Duplikationsformel und des Eulerschen Ergänzungssatzes hergeleitet werden.

Die Erfüllung einer Funktionalgleichung obigen Typs ist charakteristisch für L-Funktionen (spezielle Dirichlet-Reihen unter anderem mit analytischer Fortsetzung). Diese stehen wegen ihres Transformationsverhaltens oft in Beziehung mit Modulformen. Beispielsweise korrespondiert die Zeta-Funktion zur Jacobischen Theta-Funktion, einer Modulform halbganzen Gewichts. Aus dieser Beziehung geht, startet man mit dem Transformationsverhalten der Theta-Funktion, die Funktionalgleichung hervor.
Die Funktionalgleichung schafft einen Zusammenhang zwischen bedeutenden mathematischen Funktionen und zieht wichtige Resultate bezüglich Nullstellen- und Wachstumsverhalten der Zeta-Funktion nach sich. Sehr vielen Schlussfolgerungen ist dabei folgendes Prinzip gemein: Durch das (wegen absoluter Konvergenz der Dirichlet-Reihe) einfache Verhalten der Zeta-Funktion in der Halbebene wird automatisch eine Trivialisierung der mittels gespiegelten Halbebene erreicht.
In seiner Arbeit definierte Riemann ursprünglich für die ganze Funktion[105]
In der heutigen Konvention ist es allerdings üblicher, statt die Variable zu verwenden; man setzt dann . In dieser neuen Notation gilt dann die Reflexion
Beide Interpretationen werden heutzutage als Riemannsche Xi-Funktion bezeichnet.[106]
Die Funktionalgleichung war schon Euler (1749) bekannt, wenn er sie auch nicht für komplexe Argumente formulierte und nicht bewies, sondern nur in einer so großen Zahl von Fällen überprüfte, dass nach seinen Worten kein Zweifel an ihrer Gültigkeit bliebe.[107][108] Beweise wurden auch 1858 von Oskar Schlömilch veröffentlicht und von Carl Johan Malmstén (1849). André Weil hat darauf hingewiesen, dass ein Beweis der Funktionalgleichung mit der Mellin-Transformation schon in einem Handexemplar der Gauß’schen Disquisitiones Arithmeticae von Gotthold Eisenstein niedergeschrieben ist, mit dem Riemann in seiner Berliner Zeit eng befreundet war.[109]
Charakterisierung durch Hamburger
Im Jahre 1921 gelang es Hans Hamburger, die Riemannsche Zeta-Funktion anhand ihrer Funktionalgleichung wie folgt zu charakterisieren.
Es sei , wobei eine ganze Funktion endlicher Ordnung und eine Polynomfunktion ist, für durch die Dirichlet-Reihe darstellbar. Ferner gelte die Funktionalgleichung
wobei ebenfalls auf der Halbebene als Dirichlet-Reihe darstellbar sei. Dann folgt bereits die Identität .[110]
Transzendenz
Die Riemannsche Zeta-Funktion gehört zur Klasse der transzendenten Funktionen und sogar der hypertranszendenten Funktionen. Das bedeutet, dass sie keiner Polynomgleichung und auch keiner algebraischen Differentialgleichung (mit Koeffizienten in und algebraischen Startwerten) genügt. Dies wurde von V. E. E. Stadigh im Jahre 1902 bewiesen. Entscheidend für den Beweis war die Funktionalgleichung und ein analoges Resultat von Otto Hölder aus dem Jahr 1887[111] über die Gammafunktion:
„Wenn die Funktion und folglich auch die Funktion einer algebraischen Differentialgleichung genügt, muss nach dem im ersten Kapitel bewiesenen Satze auch der Quotient auch dieselbe Eigenschaft besitzen. Nach der obigen Funktionalgleichung ist dieser Quotient aber gleich und es ist also zu zeigen, dass die Funktion keiner algebraischen Differentialgleichung genügt.“
Global konvergente Laurent-Reihe
Als auf holomorphe Funktion mit einfachem Pol in 1 kann man die Riemannsche Zeta-Funktion um ihre Singularität in eine global konvergente Laurent-Reihe (also mit Konvergenzradius ) entwickeln. Diese hat die Form
Bei den Koeffizienten
handelt es sich um die Stieltjes-Konstanten, wobei die Euler-Mascheroni-Konstante ist,[113] für die sich daraus insbesondere der Ausdruck
ergibt.
Ordnung
Die Funktion ist ganz und hat die Wachstumsordnung 1. Das heißt, für jedes gibt es Konstanten und , sodass für alle :[114]
Hierbei ist eine andere Schreibweise für , die Exponentialfunktion. Die Bestimmung der Wachstumsordnung ist ein Zwischenschritt beim Produktsatz von Hadamard, der zur Herleitung von Riemanns Hauptformel gebraucht wird.[115]
Eigenschaften der Dirichlet-Reihe
Für reelle Argumente größer als 1
Abbildungseigenschaften und Folgerungen
Auf dem offenen Intervall ist die Zeta-Funktion eine unbeschränkte, reellwertige und streng monoton fallende Funktion. Insbesondere ist sie in diesem Bereich injektiv. Dabei ist 1 ihre größte untere Schranke, weshalb sie (wegen ihrer Stetigkeit) das Intervall bijektiv auf sich selbst abbildet. Aus ihrer Holomorphie folgt unterdessen sofort, dass sie auf beliebig oft reell differenzierbar (also glatt) ist.
Da , folgt bereits . Eine Eigenschaft analytischer Funktionen ist, unter diesen Voraussetzungen ein Spiegelungsgesetz unter der komplexen Konjugation zu erfüllen: Es gilt .[116] Dies hat wichtige Konsequenzen für die Nullstellenverteilung, da die Nullstellen an der reellen Achse gespiegelt werden und damit paarweise auftreten.
Ungleichungen
Die reelle Dirichlet-Reihe lässt sich in ihrem Konvergenzbereich durch rationale Funktionen einschließen. Es gilt für alle die Abschätzung[117]
Ebenfalls interessant in diesem Bereich ist die Ungleichung[118]
Konvergenzgeschwindigkeit
Definiert man so gilt für alle
wobei . Dies folgt aus der Euler-Maclaurin-Summenformel, die auch zur numerischen Berechnung der Zeta-Funktion herangezogen werden kann. Damit wird gezeigt, dass die Konvergenzgeschwindigkeit der Dirichlet-Reihe für kleiner werdende Realteile stark abnimmt. Zudem folgt, dass die Reihe in keinem Punkt konvergiert.
Verhalten in der vertikalen und horizontalen Richtung

Für unbegrenzt größer werdende Realteile hat die Zeta-Funktion ein leicht zu bestimmendes asymptotisches Verhalten, es gilt
Dies folgt unmittelbar aus der gleichmäßigen Konvergenz der Dirichlet-Reihe in den Bereichen und Vertauschen von Limes und Summation. Vergleiche hierzu auch den komplexen Graphen der Zeta-Funktion zu Beginn des Artikels, der in Richtung der positiven reellen Achse zunehmend konstant rot gefärbt ist.
Für jedes mit gilt
für alle . Diese Abschätzung ist optimal. Mit dem Euler-Produkt und Kroneckers Approximationssatz lassen sich nämlich zusätzlich die Aussagen
beweisen.[119] Ebenfalls mit Approximationsmethoden kann bewiesen werden, dass für jedes ein existiert, sodass[120]
gilt.
Beziehungen zu zahlentheoretischen Funktionen
Die Dirichlet-Reihen einiger elementarer und wichtiger (sehr häufig multiplikativer) zahlentheoretischer Funktionen können über die Riemannsche Zeta-Funktion ausgedrückt werden. Von großer Bedeutung ist dabei zum Beispiel die Beobachtung, dass das multiplikative Inverse der Zeta-Funktion wieder durch eine Dirichlet-Reihe dargestellt werden kann. Es gilt die Formel
wobei hier die Möbiusfunktion bezeichnet. Die Reihe zur Rechten konvergiert (wegen für alle ) absolut auf der Halbebene , und, falls die Riemannsche Vermutung richtig ist, sogar (bedingt) auf der Halbebene (was man mittels partieller Integration sieht).[121] Zur informellen Erklärung der Dirichlet-Reihen-Identität betrachtet man
also den Kehrwert des Euler-Produkts, und bildet durch konsequentes Ausmultiplizieren die dazugehörige Dirichlet-Reihe.[122]
Die Dirichlet-Faltung für zahlentheoretische Funktionen ist ein Homomorphismus vom Ring der zahlentheoretischen Funktionen in den Ring der formalen Dirichlet-Reihen . Mittels dieser ergeben sich weitere Identitäten. Für die Zahlentheorie wichtig sind dabei zum Beispiel Formeln wie
mit der Teilerfunktion oder auch
mit der Eulerschen Phi-Funktion. Es existiert darüber hinaus eine ganze Schar weiterer Identitäten. So geht zum Beispiel die Formel
auf Ramanujan zurück.[123] Diese Identitäten zeugen von einer engen Verbindung zwischen zahlentheoretischen Funktionen auf der einen Seite und einer mit guten analytischen Eigenschaften wie zum Beispiel globaler Meromorphie ausgestatteten Funktion auf der anderen Seite. Mittels Methoden der analytischen Zahlentheorie können damit oft frappierende Verhaltensmuster dieser zahlentheoretischen Funktionen bewiesen werden. Zwei wichtige Techniken dafür, die Selberg-Delange-Methode und die Verwendung von Taubersätzen, werden in diesem Artikel beschrieben.
Dirichlet-Reihe der Ableitungen und Stammfunktion
Ihre -te Ableitung besitzt für Argumente mit Realteil größer als 1 die Darstellung
Dies folgt mittels gliedweiser Differentiation, was wegen gleichmäßiger Konvergenz der Reihe auf kompakten Teilmengen erlaubt ist. Ähnlich gilt dort für eine Stammfunktion:
Spezielle Funktionswerte
Für positive gerade Argumente sind die Funktionswerte der Zeta-Funktion sämtlich bekannt. So fand Leonhard Euler die Formel
wobei die -te Bernoulli-Zahl bezeichnet.[124] Insbesondere gilt
Die Frage nach dem Wert von ist auch als Basler Problem bekannt und galt lange als ungelöst. Über die Funktionalgleichung erhält man weiter[125]
für alle . Insbesondere hat man
und es gilt für .
Im Gegensatz dazu sind geschlossene Ausdrücke für positive ungerade Werte bisher nicht bekannt. Man weiß jedoch, dass die Apéry-Konstante irrational ist. Dies wurde 1979 von Roger Apéry beweisen.[126]
Nullstellen


Triviale Nullstellen
Aus der Darstellung als Euler-Produkt kann man leicht folgern, dass für gilt. Zusammen mit der Funktionalgleichung der Zeta-Funktion und den Polstellen der Gamma-Funktion ergibt sich, dass die einzigen Nullstellen außerhalb des kritischen Streifens die „trivialen“ Nullstellen sind. Diese sind alle einfach, denn es gilt für alle
Nichttriviale Nullstellen
Neben den trivialen Nullstellen besitzt die Zeta-Funktion weitere Nullstellen im kritischen Streifen . Diese werden auch als nicht-triviale Nullstellen bezeichnet, da bis heute nur sehr wenig über deren genaue Lage bekannt ist. Aus ihrer Verbindung zur Dirichletschen Etafunktion,
kann man zumindest folgern, dass für alle reellen gilt.
Existenz und asymptotische Verteilung
Aufgrund des Euler-Produktes und der Funktionalgleichung müssen alle nicht-trivialen Nullstellen innerhalb des abgeschlossenen kritischen Streifens liegen, falls sie existieren. Dass es sogar unendlich viele nicht-triviale Nullstellen gibt, war bereits Riemann bewusst:
„Die Anzahl der Wurzeln von , deren reeller Theil zwischen und liegt, ist etwa denn das Integral positiv um den Inbegriff der Werthe von erstreckt, deren imaginärer Theil zwischen und und deren reeller Theil zwischen und liegt, ist (bis auf einen Bruchtheil von der Ordnung der Größe ) gleich ; dieses Integral aber ist gleich der Anzahl der in diesem Gebiet liegenden Wurzeln von .“
Riemann gab in seiner Arbeit also eine Formel zur asymptotischen Verteilung der nicht-trivialen Nullstellen erstmals an. Er behauptete, die Anzahl (mit Vielfachheit gerechnet) der Nullstellen innerhalb des Rechtecks erfülle die asymptotische Äquivalenz
Seinen Gedankengang begründete er (wie oben knapp beschrieben) über eine Auswertung des nullstellenzählenden Integrals
wobei die (etwas anders skalierte) Riemannsche Xi-Funktion bezeichnet, die insbesondere dieselben Nullstellen im kritischen Streifen besitzt wie die Zeta-Funktion. Diese Aussage wurde jedoch erst über 50 Jahre nach Riemanns Veröffentlichung von Mangoldt rigoros bewiesen.[128] Beim Beweis macht man sich die Funktionalgleichung zunutze. Ein von Gérald Tenenbaum gegebener Standardbeweis nutzt das erweiterte Rechteck und kommt zu
wobei wegen der ganzen Symmetrien von auch über den Linienzug integriert werden kann.[129] Mittels der einfachen Formel für logarithmische Ableitungen, und der Tatsache, dass Imaginärteile des Logarithmus über das Argument gegeben sind, folgt
Während die meisten Faktoren der -Funktion in dieser Formel leicht auszuwerten sind und die Größenordnung liefern, besteht der schwierigste Teil in der Schätzung
Der Fehler konnte bis heute nicht verbessert werden.[130] Von Littlewood stammt die Einsicht, dass die Imaginärteile der nicht-trivialen Nullstellen immer dichter zusammenrücken. Setzte man also (wobei die nach wachsenden, positiven Imaginärteilen aufsteigende Folge der nicht-trivialen Nullstellen bezeichnet), so gilt also . Dies folgert man recht direkt aus der asymptotischen Äquivalenz[130]

Symmetrieeigenschaften
Die Funktionalgleichung der Zeta-Funktion und ihre grundlegende Spiegelungseigenschaft bezüglich konjugierter Argumente implizieren ein paarweises Auftreten der nicht-trivialen Nullstellen. Ist z. B. eine Nullstelle im kritischen Streifen, so ist aufgrund der Funktionalgleichung
auch Nullstelle. Zusätzlich aber ist , weshalb auch Nullstelle ist; analog aber auch Zu bemerken ist, dass alle Werte und im kritischen Streifen liegen, dort zu einem Rechteck verbunden werden können und somit quasi ein Nullstellen-Doppelpaar bilden.
Ist jedoch die Riemannsche Vermutung richtig, so liegen alle Nullstellen auf der Geraden , wobei dann stets bzw. gilt.
Summen und Reihen
Es gilt die Identität[131]
Dabei ist die Euler-Mascheroni-Konstante. Die Reihe über alle konvergiert jedoch keinesfalls absolut. Summiert man die Absolutbeträge, ergibt sich
Diese Formel ist bei der Herleitung der expliziten Restgliedabschätzungen (auch unter Annahme der Riemannschen Vermutung) des Primzahlsatzes erforderlich.[132]
Ordnungen
Über die Ordnung der nicht-trivialen Nullstellen ist bis heute wenig bekannt. Es wird angenommen, dass alle Nullstellen der Zeta-Funktion die Ordnung 1 haben. Diese Vermutung wird von numerischen Untersuchungen unterstützt: Bisher waren alle gefundenen Nullstellen von erster Ordnung.
J. B. Conrey, A. Ghosh und S. M. Gonek fanden jedoch Aussagen unter der Annahme der Riemannschen Vermutung und der verallgemeinerten Lindelöfschen Vermutung. Letztere besagt, dass für alle und jeden Dirichlet-Charakter modulo die zugehörige L-Funktion für anwächst wie
Setzt man beides voraus, ergibt sich für die Anzahl der einfachen Nullstellen :[133]
2013 konnten H. M. Bui und D. R. Heath-Brown zeigen, dass man dies im Wesentlichen auch ohne die Lindelöfsche Vermutung beweisen kann.[134] Des Weiteren gilt für Werte
wobei über Nullstellen summiert wird. Also liegt in jedem Intervall der Imaginärteil einer einfachen Nullstelle.[135]
Nach einer Vermutung von Hardy und Littlewood existiert für jedes eine Zahl , sodass die Funktion für alle im Intervall eine Nullstelle von ungerader Ordnung hat. Zudem gibt es eine Konstante , so dass
gilt. Hierbei ist die Anzahl der Nullstellen ungerader Ordnung auf .[136]
Im Falle, dass alle Nullstellen einfach sein sollten, kommt den nicht-verschwindenden Werten eine Bedeutung zu über die für nicht-natürliche gültige Formel:
Dabei ist die Möbiusfunktion. Diese kann jedoch nur unter zusätzlichen Annahmen an das Verhalten der Zeta-Funktion im kritischen Streifen gezeigt werden; dies bezieht sich auch darauf, über welchen Intervallen die partiellen Nullstellensummen zu erstrecken sind.[137]
Nullstellenfreie Regionen
Bereits Ende des 19. Jahrhunderts konnte mit Hilfe eines einfachen Widerspruchsbeweises gezeigt werden, dass die Zeta-Funktion keine Nullstellen auf der Geraden besitzt. Grundlage dieses Beweises ist die von Mertens gezeigte, für alle mit gültige Ungleichung[138]
Diese nullstellenfreie Region konnte danach immer weiter vergrößert werden. So wurde gezeigt, dass eine Konstante existiert, sodass für keinen Wert mit
eine Nullstelle besitzt.[139] Solche Verbesserungen führen (in verallgemeinerter Form für Dirichletsche L-Funktionen) unter anderem zum Satz von Siegel-Walfisz.[140]
Das bis heute schärfste nullstellenfreie Gebiet, mit großem technischem Aufwand gewonnen, ist für gegeben durch[141]
Dieses führt beim Primzahlsatz zu einem verbesserten Fehler: Für eine Konstante gilt[142][143]
Ein expliziter Wert für die Konstante in der Fehlerfunktion, nämlich , wurde 2002 von Ford gegeben.[144] Insbesondere ist nicht bekannt, ob es ein gibt, sodass gilt für alle mit .[145]
Die Riemannsche Vermutung

Riemann vermutete im Jahr 1859, dass alle nicht-trivialen Nullstellen auf der parallel zur imaginären Achse verlaufenden Geraden liegen. Wegen der Funktionalgleichung ist dies äquivalent zu für alle . Diese sogenannte Riemannsche Vermutung konnte bislang weder bewiesen noch widerlegt werden.
Die Lage der Nullstellen im kritischen Streifen hängt eng mit Aussagen über die Verteilung der Primzahlen zusammen. Beispielsweise ist die Aussage, dass auf dem Rand des kritischen Streifens keine Nullstellen liegen, ein möglicher Zwischenschritt beim Beweis des Primzahlsatzes. Mit anderen Worten: Die Nullstellen kodieren die Abweichung der Primzahlfunktion von der durch den Primzahlsatz gegebenen Größenordnung (Integrallogarithmus). Deren (durch das nicht mehr konvergente Euler-Produkt) gewährleistete Existenz ist also als natürliche Barriere zu verstehen, die eine gewisse Unschärfe bei der Identifikation als Tribut fordert. Doch obwohl man weiß, dass diese Unschärfe natürlicherweise existiert, ist ihre Intensität nicht geklärt und hängt mit der Verteilung der Nullstellen zusammen. Je näher sich Nullstellen an der Geraden befinden, desto größer werden die Abweichungen sein. Gilt für alle mit , so folgt für alle [147]
Liegen jedoch alle Nullstellen auf der mittleren Geraden , so ist diese Unschärfe kleinst möglich (man beachte, dass mit auch nicht-triviale Nullstelle ist). Dies hätte eine erstaunliche Glattheit bei der Verteilung der Primzahlen zur Folge, zum Beispiel gölte nach Lowell Schoenfeld dann ganz explizit[148]
Hierbei ist zu beachten, dass zwar beliebig groß wird, jedoch asymptotisch betrachtet deutlich kleiner als ist.
Atle Selberg gab 1946 folgende Einschätzung:
„Ich denke, wir glauben deshalb so gerne an die Richtigkeit der Riemannschen Vermutung, weil es die schönste und einfachste Verteilung für die Nullstellen ist, die wir uns vorstellen können. Es gibt diese Symmetrie entlang der kritischen Geraden. Außerdem hätte sie die natürlichste Verteilung der Primzahlen zur Folge. Irgendwie möchten wir gerne glauben, dass zumindest etwas in diesem Universum richtig sein sollte.“
Resultate zur Lage auf der kritischen Geraden

Im Jahr 1914 konnte Godfrey Harold Hardy zeigen, dass unendlich viele nicht-triviale Nullstellen auf der kritischen Geraden liegen. In seinem damals revolutionären Beweis machte er sich zunutze, dass für alle reellen Zahlenwerte der Ausdruck
nur reelle Funktionswerte annimmt. Dies vereinfachte das Problem auf die zu klärende Existenz unendlich vieler Nullstellen einer reellwertigen Funktion. Der durch Widerspruch geführte Beweis (siehe Reductio ad absurdum) zeigt auf, dass für unendlich oft sein Vorzeichen wechseln muss, was mit dem Zwischenwertsatz schon zeigt, dass unendlich viele Nullstellen auf besitzt.[150]
1921 verbesserte Hardy zusammen mit seinem Freund und Kollegen John Edensor Littlewood die Aussage auf das wesentlich stärkere Resultat, dass für hinreichend große Werte die Anzahl der Nullstellen auf der kritischen Geraden im Segment mindestens beträgt, wobei eine positive Konstante bezeichnet.
Atle Selberg verbesserte dieses Ergebnis 1942 auf [151] und zeigte außerdem, dass ein positiver Anteil aller Nullstellen auf der kritischen Geraden liegen.[152] Es gibt also eine Konstante , sodass
Für diesen und andere Beiträge wurde er im Jahre 1950 mit der Fields-Medaille geehrt. Ab diesem Punkt wurde daran gearbeitet, möglichst hohe Werte für zu finden.
Anfang der 1970er Jahre konnte Norman Levinson zeigen, dass mindestens ein Drittel () der nicht-trivialen Nullstellen auf der kritischen Geraden liegen muss, wobei jedoch als hinreichend groß vorausgesetzt wird.[153] 1989 verbesserte Conrey diesen Wert auf , wobei er Techniken von Levinson verfeinerte.[154]
Numerische Berechnungen
Bereits früh gab es Anstrengungen, die Riemannsche Vermutung und andere Phänomene durch explizite numerische Berechnungen zu überprüfen. Die Methoden wurden, insbesondere im Zeitalter von leistungsstarken Computern, explosionsartig besser. Bisher liegen alle gefundenen nicht-trivialen Nullstellen auf der Geraden . Da es unendlich viele nicht-triviale Nullstellen gibt, können Algorithmen jedoch höchstens für die Suche eines Gegenbeispiels und nicht für einen Beweis der Riemannschen Vermutung herangezogen werden.
Numerische Werte der frühen Nullstellen
Die Imaginärteile der „ersten“ Nullstellen sind beispielsweise[155]
| ±k | ±Im(ρk) | ±k | ±Im(ρk) |
|---|---|---|---|
| 1 | 14,134725141734693790… | 11 | 52,970321477714460644… |
| 2 | 21,022039638771554993… | 12 | 56,446247697063394804… |
| 3 | 25,010857580145688763… | 13 | 59,347044002602353079… |
| 4 | 30,424876125859513210… | 14 | 60,831778524609809844… |
| 5 | 32,935061587739189690… | 15 | 65,112544048081606660… |
| 6 | 37,586178158825671257… | 16 | 67,079810529494173714… |
| 7 | 40,918719012147495187… | 17 | 69,546401711173979252… |
| 8 | 43,327073280914999519… | 18 | 72,067157674481907582… |
| 9 | 48,005150881167159727… | 19 | 75,704690699083933168… |
| 10 | 49,773832477672302181… | 20 | 77,144840068874805372… |
Über die Eigenschaften dieser Imaginärteile (Irrationalität, Transzendenz …) ist bis heute nichts bekannt.[156]
Hadamard-Produktentwicklung
Neben dem Euler-Produkt gibt es eine weitere Produktdarstellung der Zeta-Funktion, die erstmals ihre Nullstellen in eine mögliche Definition direkt mit einschließt. Diese ist so bedeutend, weil sie der Schlüssel für den Zusammenhang zwischen Primzahlen und Nullstellen ist. Der entscheidende Schritt in Bernhard Riemanns Arbeit war nämlich der „Vergleich“ dieser beiden Produkte, was schließlich ein enges Verhältnis zwischen den Produktelementen (in diesem Falle Primzahlen und Nullstellen) impliziert. Wegen ihrer niedrigen Konvergenzgeschwindigkeit ist die Produktdarstellung jedoch in der Praxis nicht als Grundlage für einen numerischen Berechnungsalgorithmus für die Zeta-Funktion geeignet.
Über den Produktsatz von Hadamard für holomorphe Funktionen ist es möglich, die Zeta-Funktion anhand ihrer Nullstellen über ein Produkt zu rekonstruieren. Dabei wird ausgenutzt, dass die ganze Funktion die Wachstumsordnung 1 besitzt.[157] Demnach gibt es Konstanten und , so dass
Dabei ist und .[158] Damit erhält man das Hadamard-Produkt,[159] benannt nach seinem Entdecker Jacques Hadamard, das global in konvergiert:
Eine etwas einfachere (jedoch nur bedingt konvergente) Form des Hadamard-Produktes ist
Absolute Konvergenz ergibt sich, wenn man die Nullstellen „paarweise“ ordnet. Es werden damit die Faktoren unter Indexierung betrachtet.
Weitere Eigenschaften im kritischen Streifen


Universalitätssatz von Woronin
Nach dem Universalitätssatz von Woronin ist die Riemannsche -Funktion imstande, jede beliebige holomorphe Funktion in einer nullstellenfreien Kreisscheibe mit Radius 1/4 beliebig genau zu approximieren.
Als anschaulichen Vergleich stelle man sich dafür vor, dass es für jede holomorphe Funktion eine Art „Landkarte“ gibt, die Höhen und Tiefen sowie Himmelsrichtung der Funktionswerte in der komplexen Ebene darstellt. Der Universalitätssatz besagt nun, dass man, wenn man die Landkarte der Zeta-Funktion in einem bestimmten unendlichen Bereich scannen würde, früher oder später auf Gebiete stieße, die Ausschnitten der Landkarten anderer Funktionen, also mitsamt allen darin eingetragenen „Bergen“ und „Tälern“, beliebig ähneln. Als einzige Voraussetzung gelte hierbei jedoch, dass auf dem Kartenausschnitt der fremden Funktion nie der Wert 0 eingetragen sei.
Formal ausgedrückt: Sei eine kompakte Teilmenge des Streifens mit zusammenhängendem Komplement. Sei nun eine stetige Funktion, die holomorph im Innern von sei und für kein verschwinde. Es existiert dann für jedes ein , sodass
für alle . Zu beachten ist hierbei, dass es sich im Allgemeinen nur um eine Approximation handelt, also gewährleistet werden muss. Hätte man für eine Teilmenge mit Häufungspunkt im Inneren von , so folgte mit dem Identitätssatz für holomorphe Funktionen bereits auf ganz .
Es gilt sogar noch mehr: Die untere asymptotische Dichte aller , die eine Approximation erfüllen, ist positiv, wie die Ungleichung
beweist. Hier ist das Standard-Lebesgue-Maß auf den reellen Zahlen.[160] Für sehr kleine Kreisscheiben können sogar effektive Schranken angegeben werden, falls bestimmte Voraussetzungen erfüllt. So existiert für alle in analytischen mit und eine Zahl , sodass
Ein ähnliches Resultat findet sich auch für die untere asymptotische Dichte.[161] Es ist zu beachten, dass in dieser Version die modifizierte Funktion universell ist.
Diese erstaunliche Eigenschaft zieht einige Konsequenzen nach sich. Zum Beispiel lässt sich zeigen, dass die Riemannsche Zeta-Funktion keiner algebraischen Differentialgleichung gehorcht. Genauer gesagt kann man zeigen: Sind eine stetige Funktion, Konstanten, natürliche Zahlen mit , sodass
so folgt bereits .[162] Ist zudem mit beliebig gewählt, folgt, dass die Menge
Approximate functional equation
Obwohl die Dirichlet-Reihe im kritischen Streifen nicht mehr konvergiert, können ihre Partialsummen zu einer guten Approximation der Zeta-Funktionen führen. Eine sehr einfache Formel dieses Typs, gültig für , ist beispielsweise
Für feste Werte wird der Fehler für hinreichend große Werte klein. Jedoch ist ein schwerer Nachteil für große Imaginärteile.[164] Um dem entgegenzuwirken, wird fest gewählt. Unter Zuhilfenahme der van-der-Corputschen-Summenformel kann für das Restglied weiter verbessert werden zu
indem der Summationsbereich an das Argument angepasst wird. Damit lässt sich die Zeta-Funktion in durch die ersten Glieder der Dirichlet-Reihe annähern. Im Bereich folgt mittels der Funktionalgleichung die folgende Darstellung durch eine Dirichlet-Reihe:
Auch hier ist eine entsprechende Annäherung im kritischen Streifen zu erwarten und kombiniert man beide Ergebnisse, so ergibt sich mit und , die Formel
die auch Approximate functional equation genannt wird.[165] Diese wurde 1921 von Hardy und Littlewood entdeckt, jedoch war sie, wie sich später herausstellte, bereits Bernhard Riemann bekannt.[166] Sie ist ein mächtiges Werkzeug zur Untersuchung der Zeta-Funktion im kritischen Streifen.
Wachstum im kritischen Streifen
Bekannte Resultate
Mit der Approximate functional equation folgt über
Korobov und Vinogradov haben 1958 die Abschätzung
mit einem bewiesen.[167][168][169] Für die Gerade zeigten sie damit
Eine explizitere Form gab Richert im Jahr 1967:[170]
Aus diesen Resultaten lässt sich das bisher größte bekannte nullstellenfreie Gebiet von bestimmen.[171] Innerhalb diesem gelten die Abschätzungen[172]
und
Die Lindelöfsche Vermutung

Für alle reellen ist die Größe
endlich. Die Notation ist dabei historisch bedingt.[173] Sie ist ein Maß dafür, wie schnell die Riemannsche Zeta-Funktion entlang vertikaler Geraden anwächst. Für reelle Zahlen außerhalb des kritischen Streifens lässt sich leicht berechnen. Für gilt , da für alle Werte mit nach Abschätzung der Summe mittels absoluter Konvergenz folgt, erhält man . Über die Möbius-Funktion folgt andererseits die untere Schranke , weshalb gleichzeitig und damit bewiesen ist. Zusammen mit diesem Resultat folgt über die Stirlingsche Formel und die Funktionalgleichung der Zeta-Funktion für alle .[173] Ebenfalls gesichert sind die Randwerte sowie .[174]

Die genauen Werte von für kritische Werte sind bis heute (September 2023) unbekannt. Schuld daran ist, dass Größencharakterisierungen dieser Genauigkeit ohne absolute Konvergenz sehr schwierig und mitunter unmöglich sind. Es wird vermutet, dass die Zeta-Funktion in den vertikalen Bereichen zu weiterhin langsam anwächst, also gilt, jedoch nicht mehr zwangsläufig durch eine Konstante beschränkt ist. Dies ist äquivalent zu für alle . Diese Aussage wird auch als Lindelöfsche Vermutung (nach Ernst Leonard Lindelöf) bezeichnet und ist bis heute unbewiesen.[175] Es ist aber bekannt, dass die Funktion auf jeder vertikalen Geraden mit unbeschränkt ist.[176]
Trotz allem kann man Abschätzungen für das Verhalten von angeben. Über die Approximate functional equation folgert man beispielsweise
Man kann außerdem zeigen, dass konvex[174] ist und dass die folgende Abschätzung nach unten gilt:[174]
Die Lindelöfsche Vermutung ist äquivalent dazu, dass in der letzten Ungleichung stets Gleichheit gilt. Wegen der Konvexität von und der Funktionalgleichung der Zeta-Funktion ist dies bereits gleichbedeutend mit .
Zusammenhang zu Potenzmomenten
Die zahlentheoretische Bedeutung der Lindelöfschen Vermutung wird durch einen Zusammenhang zu den Potenzmomenten der Zeta-Funktion entlang der kritischen Geraden ersichtlich. Definiert man
so ist sie äquivalent zu der Aussage für alle Werte . Die Potenzmomente tauchen unter anderem bei Fehlerabschätzungen im Dirichletschen Teilerproblem und in der Statistik auf. Explizit gilt[177]
und Heath-Brown zeigte 1979[178][179]
mit und berechenbaren . Die Momente der Zeta-Funktion sind, besonders für große Werte (wo die Theorie deutlich schwieriger ist), ein hochaktuelles Forschungsgebiet. Beiträge lieferten Conrey, Gonek[180] für große Werte und Heath-Brown[181] für rationale . Im Zusammenhang mit der Theorie der Zufallsmatrizen haben Keating und Snaith eine Vermutung über das genaue asymptotische Verhalten der Potenzmomente formuliert.
Zusammenhang mit der Riemannschen Vermutung
Zwischen dem Wachstum einer analytischen Funktion und der Anzahl ihrer Nullstellen besteht wegen der Jensenschen Formel ein Zusammenhang. Tatsächlich gilt die Lindelöfsche Vermutung genau dann, wenn für alle gilt:[182]
Dies wurde erstmals 1918 von Backlund bewiesen.[183][184] Ist die Riemannsche Vermutung richtig, so wäre der Zähler stets 0, womit die Lindelöfsche Vermutung direkt folgt. Jedoch kann aus der Gültigkeit der Lindelöfschen Vermutung nicht die der Riemannschen Vermutung gefolgert werden, da schon eine einzige nicht-triviale Nullstelle mit Realteil ungleich genügt, um letztere zu widerlegen.
Im Falle, dass die Riemannsche Vermutung wahr ist, zeigte Littlewood[185]
mit einer positiven Konstanten . Soundararajan zeigte, dass in diesem Fall gesetzt werden kann.[186]
Anwendung in der analytischen Zahlentheorie
Zusammenhang zur Primzahlverteilung
Der Primzahlsatz
Wie bereits der 15-jährige Gauß vermutete, wächst die Anzahl aller Primzahlen unter einer gegebenen Schranke asymptotisch gleich wie der Ausdruck . Es gilt also:
Dieser sogenannte Primzahlsatz wurde jedoch erst hundert Jahre später unabhängig von Hadamard und Poussin bewiesen. Für einen Beweis kann die zwischen der Riemannschen Zeta-Funktion und der Primzetafunktion geltende Identität
genutzt werden, die ihren Ursprung im Euler-Produkt findet. Weiß man nun, dass für alle , so folgt, dass sich auf das Geradenstück holomorph fortsetzen lässt und in einer Umgebung von in der Form mit einer holomorphen Funktion geschrieben werden kann. Mit dem Taubersatz von Delange folgt damit bereits[187]
Dabei bezeichnet den Integrallogarithmus. Ein anderer elementarerer Ansatz verwendet die Mangoldt-Funktion und den Taubersatz von Wiener-Ikehara.[188] Eine „schnelle“ Methode stammt von Donald Newman und verwendet die Möbiusfunktion.[189][190]
Explizite Berechnung der Primzahlfunktion

Aus der unbedingten Konvergenz des Euler-Produktes folgt unmittelbar, dass auf der Halbebene keine Nullstellen besitzt. Ferner gilt dort die Identität woraus Riemann schließlich den für alle gültigen, zahlentheoretisch sehr wichtigen Ausdruck
mittels inverser Mellin-Transformation hervorbringen konnte. Die Summe auf der linken Seite liefert für jede Primzahlpotenz jeweils den Beitrag , kann also mit identifiziert werden. Hierbei bezeichnet die Primzahlfunktion, die zählt, wie viele Primzahlen kleiner als sind. Riemann berechnete das rechte Integral mittels eines Vorläufers des Hadamard-Produktes und fand damit die für nicht-ganze Zahlen gültige explizite Formel[192]
wobei den Integrallogarithmus bezeichnet. Über Möbius-Inversion kann aus der Wert rekonstruiert werden:[193]
Hierbei ist die Möbiusfunktion. Über die nicht-trivialen Nullstellen kann also der Wert der Primzahlfunktion an der Stelle exakt berechnet werden. Insbesondere ist eine vollständige Fehlerkorrektur des Primzahlsatzes möglich. Bezüglich Konvergenz ist zu beachten, dass die Summe über die Nullstellen nach ihrer Konjugation paarweise addiert. Des Weiteren sind die Terme in der Summe als zu verstehen (hier bezeichnet die (komplexe) Integralexponentialfunktion), denn: Verwechslungen können bei der Auswertung von über den Hauptzweig des komplexen Logarithmus entstehen.
Den „reellen Hauptteil“ seiner Formel interpretierte Riemann als bessere Approximation als an . Er hob auch die mögliche Bedeutung der Nullstellen („periodische Glieder“) bei der Entschlüsselung der unregelmäßigen Abstände zwischen Primzahlen hervor:
„Die bekannte Näherungsformel ist also nur bis auf Größen von der Ordnung richtig und giebt einen etwas zu grossen Werth; denn die nicht periodischen Glieder in dem Ausdrucke von sind, von Größen, die mit nicht ins Unendliche wachsen, abgesehen: . In der That hat sich bei der von Gauss und Goldschmidt vorgenommenen und bis zu = drei Millionen fortgesetzten Vergleichung von mit der Anzahl der Primzahlen unter diese Anzahl schon vom ersten Hunderttausend an stets kleiner als ergeben, und zwar wächst die Differenz unter manchen Schwankungen allmählich mit . Aber auch die von den periodischen Gliedern abhängige stellenweise Verdichtung und Verdünnung der Primzahlen hat schon bei den Zählungen die Aufmerksamkeit erregt, ohne dass jedoch hierin eine Gesetzmässigkeit bemerkt worden wäre. Bei einer etwaigen neuen Zählung würde es interessant sein, den Einfluss der einzelnen in dem Ausdrucke für die Dichtigkeit der Primzahlen enthaltenen periodischen Glieder zu verfolgen.“

Die von Riemann angesprochene Funktion
wird heutzutage als Riemannsche R-Funktion bezeichnet[195] und liefert für die ersten Werte eine (stellenweise deutlich) bessere Approximation von als . Da jedoch Littlewood zeigen konnte, dass die Funktion unendlich viele Nullstellen besitzt,[196] kann das nicht für alle der Fall sein. Lediglich denkbar wäre eine „durchschnittlich“ bessere Annäherung im Sinne
für alle (hinreichend großen) , aber das ist bis heute unbekannt.[197]
Die Selberg-Delange-Methode
Bei der Selberg-Delange-Methode handelt es sich um eine Technik, die mittlere Ordnung einer zahlentheoretischen Funktion zu bestimmen, solange ihre erzeugte Dirichlet-Reihe hinreichend gute Eigenschaften besitzt. Hierbei macht man sich komplexe Potenzen der Zeta-Funktion zunutze. Für betrachtet man und findet mit dem Euler-Produkt für alle :
Sei dafür eine Dirichlet-Reihe, die auf der Halbebene konvergiert. Falls sich für ein die Funktion holomorph in eine nullstellenfreie Region von fortsetzen lässt und dort ein gut kontrolliertes Wachstum besitzt, kann die Summe
explizit geschätzt werden.[198] Der Fehler hängt dabei von der Größe des nullstellenfreien Gebietes von ab. Ein Vorteil dieser Methode ist, dass bis auf Konvergenz der Reihe keine wesentlichen Voraussetzungen an die Terme gestellt werden. Nachteilig ist die notwendige Wachstumsbedingung an die Funktion .
Ein Anwendungsbeispiel der Selberg-Delange-Methode ist ein Resultat von Paul Bateman bezüglich der Eulerschen Phi-Funktion. Dieses besagt, dass die Anzahl der natürlichen Zahlen , für die gilt, asymptotisch durch[199]
gegeben ist, wobei eine Konstante ist. Die dafür betrachtete Dirichlet-Reihe hat für die Gestalt
Das Dirichletsche Teilerproblem
Die Lindelöfsche Vermutung ist bereits eine zahlentheoretische Aussage. Sie kann dazu verwendet werden, die Natur von Teilersummen recht detailliert zu beschreiben. Diese Summen sind Gegenstand des Dirichletschen Teilerproblems, das in der klassischen Variante nach der Größenordnung der Summe
fragt, wobei hier die Anzahl der positiven Teiler von bezeichnet. In etwa ist , da die 6 die Teiler 1, 2, 3 und 6 hat. Bereits Peter Gustav Lejeune Dirichlet zeigte:
mit . Das Teilerproblem fragt nun nach der Natur der Zahlen , die in diese Gleichung eingesetzt werden dürfen. Im Jahr 1922 zeigte J. van der Corput [200] und die Abschätzung wurde von M. N. Huxley im Jahr 2003 angegeben.[201] Auf der anderen Seite zeigten G. H. Hardy und E. Landau, dass gelten muss.[202]
Dieses Problem lässt sich sogar noch verallgemeinern. Dazu definiert man
Während ist und alle Paare mit abzählt (mit anderen Worten die Teiler von ), zählt alle Tupel mit ab.
Mit Hilfe der Potenzmomente der Riemannschen Zeta-Funktion kann die allgemeine Aussage
getroffen werden.[203] Der Term ist durch das Residuum der Funktion an der Stelle 1 gegeben. Hintergrund dieses Zusammenhangs ist, dass die Dirichlet-Reihe der Funktion durch die erzeugt wird.[204] Falls nun aber die Lindelöfsche Vermutung wahr ist, und nur dann, kann dieser Fehler für alle durch für alle ersetzt werden.[205] Aus mit einem Polynom vierten Grades folgt beispielsweise [203]
Produktkompositionen

Eine Produktkomposition der natürlichen Zahl ist von der Form mit natürlichen Zahlen . Bezeichnet die Anzahl aller Produktkompositionen (die Reihenfolge der Faktoren spiele eine Rolle) von , so gilt nach der geometrischen Reihe für Zahlen mit hinreichend großem Realteil, wenn man fordert,
Dies wurde von László Kalmár genutzt, die folgende asymptotische, für jedes gültige, Formel zu entwickeln:[206]
Dabei ist die einzige Lösung der Gleichung im Intervall . Diese wird heutzutage auch als Kalmársche Kompositionskonstante bezeichnet.[207] Kalmár selbst gab die Abschätzung . Inzwischen wurden die Ergebnisse weiter verfeinert.[208]
Bestimmung der mittleren Ordnung zahlentheoretischer Funktionen über Taubersätze
Taubersätze für Dirichlet-Reihen mit gelten bereits unter recht schwachen Voraussetzungen. So lassen sich Wachstumsformeln für summatorische Funktionen
bereits daraus ableiten, dass die zugehörigen Dirichlet-Reihen auf einer Halbebene konvergieren, an der Stelle einen singulären Punkt haben (d. h., dass sich die durch die Dirichlet-Reihe dargestellte holomorphe Funktion für keine offene Menge holomorph nach fortsetzen lässt) und sich ansonsten von rechts holomorph auf die Gerade fortsetzen lassen. Kompositionen der Riemannschen Zeta-Funktionen erfüllen sehr oft diese Bedingungen.
So folgt aus für reellwertige bereits
Für die Phi-Funktion ergibt sich mit
Gutes Werkzeug zur Herleitung dieser Identitäten ist der Taubersatz von Delange. Für den Fall, dass die betrachtete zahlentheoretische Funktion gerade Indikatorfunktion einer Teilmenge ist, geben Taubersätze Auskunft über deren asymptotische Dichte. Der Primzahlsatz, der den Fall (Menge der Primzahlen) behandelt, ist ein solches Dichteresultat.
Quaternionen und Oktaven
Über das Cayley-Dickson-Verfahren kann man aus den Quaternionen und Oktaven Dirichlet-Reihen bestimmen, welche die Quadratsummen-Funktion bzw. beinhalten, nämlich[209]
und auch
Daraus folgt unter anderem unmittelbar der Vier-Quadrate-Satz und der Satz von Jacobi.
Zusammenhänge zu elliptischen Kurven und kongruenten Dreiecken

Die (globale) Hasse-Weil -Funktion einer elliptischen Kurve über hat die Gestalt
wobei die lokalen Zeta-Funktionen zu bezeichnen.[210]
Ein Dreieck wird als kongruent bezeichnet, falls es rechtwinklig ist, ausschließlich rationale Seitenlängen und einen ganzzahligen Flächeninhalt besitzt. Die Zahl wird entsprechend als kongruente Zahl bezeichnet. Eine Zahl ist genau dann eine kongruente Zahl, falls die zugehörige elliptische Kurve unendlich viele rationale Punkte besitzt. Gilt die schwache Vermutung von Birch und Swinnerton-Dyer, ist dies genau dann der Fall, falls .[211] Unter dieser Voraussetzung kodiert die oben definierte Hasse-Weil -Funktion die geometrischen Eigenschaften der Zahlen bezüglich Kongruenz.[212]
Verallgemeinerungen
In dem Wunsch, die Definition der Riemannschen Zeta-Funktion zu verallgemeinern oder zu variieren, wurden zahlreiche verwandte Funktionen eingeführt und untersucht. Häufig tragen diese ebenfalls den Namen „Zeta-Funktion“, verbunden mit dem Namen ihres „Entdeckers“. Vorweg sei vor diesem Hintergrund auch auf die Liste von Zeta-Funktionen verwiesen.
Dirichletsche L-Funktionen
Die Riemannsche Zeta-Funktion ist eine spezielle Dirichletsche L-Funktion. Dabei wird zunächst einem Dirichlet-Charakter (einer periodischen, streng multiplikativen zahlentheoretischen Funktion) eine Dirichlet-Reihe mit Euler-Produkt zugeordnet via
Erneut ist diese Darstellung nur für Werte gültig, und die Funktionen lassen sich analytisch auf ganz fortsetzen, wobei in ein Pol erster Ordnung im Falle eines Hauptcharakters, d. h., nimmt an allen Stellen ungleich Null bloß den Wert 1 an, und ansonsten eine hebbare Singularität vorliegt. In letzterem Fall dehnt sich sogar zu einer ganzen Funktion aus. Die verallgemeinerte Riemannsche Vermutung besagt nun, dass alle (nichttrivialen) Nullstellen von im Streifen den Realteil haben.[213] Die Riemannsche Zeta-Funktion entspricht damit der Dirichletschen L-Funktion zum trivialen Charakter, der stets den Wert 1 annimmt. Aus der verallgemeinerten Riemannschen Vermutung folgt somit die Riemannsche Vermutung mit als Spezialfall.
Hurwitzsche und Lerchsche Zeta-Funktion
Definiert wird die Hurwitzsche Zeta-Funktion für und durch
Für festes besitzt sie eine analytische Fortsetzung auf mit einem einfachen Pol in . Für gilt nun:
Mit Hilfe der Hurwitzschen Zeta-Funktion lassen sich die Riemannsche Zeta-Funktion und die Dirichletschen L-Funktionen einheitlich behandeln. Dies ist vor allen Dingen bezüglich deren verallgemeinerter Funktionalgleichung von Nutzen.
Sogar noch allgemeiner als die Hurwitzsche Zeta-Funktion ist die Lerchsche Zeta-Funktion, welche für , und gegeben ist durch
Es gilt dann
Die weitreichende Definition der Lerchschen Zeta-Funktion gestattet nicht nur Spezialisierungen zur Hurwitzschen und somit auch zur Riemannschen Zeta-Funktion, sondern beinhaltet noch viele andere wichtige Funktionen als Spezialfälle. Ähnlich definierte „verallgemeinerte Zeta-Funktionen“ werden auch in der theoretischen Physik verwendet, und zwar im Zusammenhang mit der systematischen sogenannten semiklassischen Näherung quantenmechanischer Resultate.
Dedekindsche Zeta-Funktion zu Zahlkörpern

Die Dedekindsche Zeta-Funktion eines Zahlkörpers verallgemeinert die Riemannsche Zeta-Funktion. Dabei befasst sich mit der „Primfaktorzerlegung“ im Ganzheitsring von . Der Ring ist die Menge aller Elemente , die Lösung einer Polynomgleichung mit ganzen Zahlen sind.[214] Zum Beispiel ist und . Die Frage, ob es allgemein in eine eindeutige Zerlegung in Primelemente gibt, ist von zahlentheoretischer Relevanz und ihre Antwort lautet im Allgemeinen „Nein“. So sind die Zahlen zwar alle prim und paarweise verschieden in , jedoch gilt
Um Eindeutigkeit wieder herzustellen, wird auf die Ideale von übergegangen. Vor diesem Hintergrund entwickelte Ernst Eduard Kummer die Idee der „idealen Zahlen“, die jedoch als überholt gilt.[215] Jedes nicht-triviale ganze Ideal besitzt eine eindeutige multiplikative Zerlegung in Primideale. Dies ermöglicht schließlich die Definition einer Zeta-Funktion
die in ein Euler-Produkt über die Primideale zerfällt:[216]
Hierbei bezeichnet die natürliche Zahl die Norm des Ideals (ein Maß für seine „Dichte“ in ).
Die Funktion besitzt eine holomorphe Fortsetzung nach , hat einen Pol erster Ordnung in und erfüllt eine Funktionalgleichung.[217] Sie besitzt große zahlentheoretische Relevanz, da sie einerseits das Konzept der Riemannschen Vermutung auf Zahlkörper ausweitet, andererseits in der Klassenzahlformel kodiert, „wie stark“ die Primfaktorzerlegung in von der Eindeutigkeit abweicht.[218] Dieses Maß ist auch als Klassenzahl bekannt.[219]
Der Zahlkörper der rationalen Zahlen
Im Falle ist die Dedekindsche Zeta-Funktion gerade die Riemannsche Zeta-Funktion. Insbesondere hängt diese mit den Primelementen in deren Ganzheitsring zusammen.[220]
Quadratische Zahlkörper
Ist eine quadratische Erweiterung von mit Diskriminante , so gibt es einen Dirichlet-Charakter modulo , sodass
wobei die zu gehörige Dirichletsche L-Funktion bezeichnet.[221]
Ein wichtiger Spezialfall ist . Die dazu korrespondierende Zeta-Funktion ist gegeben durch
wobei die Dirichletsche Betafunktion zum Charakter modulo 4 korrespondiert. Daraus ergibt sich direkt die folgende Identität für die Dirichlet-Reihe der Quadratsummen-Funktion :[222]
Über einen Koeffizientenvergleich kann man damit auf eine geschlossene Formel für die schließen. Dies liefert unter anderem einen analytischen Beweis dafür, dass eine Primzahl genau dann Summe zweier Quadrate ist, also , wenn
Kreisteilungskörper
Ist der Körper der -ten Einheitswurzeln, auch genannt Kreisteilungskörper, dann gilt[223]
Das Produkt durchläuft hierbei alle primitiven Charaktere modulo sodass mit Ausnahme des trivialen Charakters , der nur den Wert 1 annimmt. Da sowohl als auch einfache Pole bei besitzen, folgt, dass gilt für alle Charaktere. Eine Konsequenz dieser Aussage ist der Dirichletsche Primzahlsatz.[224]
Abelsche Erweiterungen
Im Falle, dass eine Abelsche Erweiterung ist, ist der Quotient eine ganze Funktion. D. h. gewissermaßen, dass die Riemannsche Zeta-Funktion in diesem Falle ein „Teiler von “ ist (Satz von Aramata-Brauer).[225] Dass dies auch für nicht-abelsche Erweiterungen richtig ist, ist Gegenstand tiefer zahlentheoretischer Vermutungen, zum Beispiel der Dedekindschen Vermutung[226] oder der Artinschen Vermutung.
Arithmetische Zeta-Funktionen
Die Zeta-Funktion eines Schemas (von endlichem Typ über den ganzen Zahlen) ist definiert durch das Euler-Produkt
Das Produkt durchläuft hierbei alle abgeschlossenen Punkte des Schemas, also jene, deren zugehöriger Restklassenkörper endlich ist. bezeichnet die Anzahl der Elemente dieses Körpers. Dem affinen Schema zugehörig ist dann die Riemannsche Zeta-Funktion.
Zusammenhänge zur Theorie der automorphen Formen
In der Theorie der für die Zahlentheorie wichtigen Modulformen taucht die Riemannsche Zeta-Funktion an einigen Stellen auf.
L-Funktionen zu Eisensteinreihen
Für die Gewichte werden die normierten Eisensteinreihen zur vollen Modulgruppe wie folgt definiert:[227]
Bei letzterem Ausdruck handelt es sich um eine Darstellung als Fourierreihe. Diese ist charakteristisch für Modulformen. Aufgrund der Normierung mittels des Faktors hat diese nun ausschließlich rationale Koeffizienten. Das wird in der Zahlentheorie u. a. dazu benutzt, ganzzahlige Identitäten zwischen Teilerfunktionen zu beweisen.[228] Wegen ihrer Beziehung zu Teilerfunktionen (die Koeffizienten der zu den gehörigen Fourierreihen) sind die zu gehörigen L-Funktionen. Dieses Prinzip verallgemeinert sich für Eisensteinreihen zu Kongruenzuntergruppen. Hier hängen die konstanten Koeffizienten mit Werten von L-Funktionen zu Dirichlet-Charakteren zusammen.
1987 konnte Frits Beukers die Irrationalität von mit Hilfe der Theorie der Eisensteinreihen beweisen. Dafür betrachtete er die Funktion
die eine Modulform zum Gewicht 4 für die Kongruenzuntergruppe ist. Die zu diesem korrespondierende L-Funktion ist dann
Das Argument bezieht sich letztlich auf eine Technik, die Konvergenzradien von Umkehrfunktionen lokal injektiver, meromorpher Funktionen ausnutzt.[229] Mit der gleichen Methode lassen sich auch und zeigen, wobei der Charakter das Legendre-Symbol modulo 5 ist.[230] Die Techniken lassen sich jedoch laut Beukers selbst höchstwahrscheinlich nicht auf die Fälle übertragen, geben jedoch Einblick in algebraisch geometrische und modulare Interpretationen der Apery-Zahlen.[231]
Beziehung zu nicht-holomorphen Eisensteinreihen
Für komplexe Zahlen mit und mit konvergiert die Eisensteinreihe
absolut. Die dadurch definierte Funktion ist nicht-holomorph und zudem (für fixierte ) invariant in unter Wirkung der vollen Modulgruppe. Zudem lässt sie sich (für fixierte ) in meromorph in die gesamte Ebene fortsetzen mit einfachen Polen in und , es gilt die Funktionalgleichung
Diese Parallele zur Theorie der Zeta-Funktion lässt bereits einen Zusammenhang vermuten. Es gilt die Darstellung[232]
wobei die Untergruppe der Translationen von bezeichnet. Betrachtet man zudem die Fourierentwicklung
so gilt[233]
Nicht-holomorphe Eisensteinreihen, und damit auch die Zeta-Funktion selbst, spielen eine fundamentale Rolle bei der sogenannten Rankin-Selberg-Methode, die sich als mächtiges Werkzeug bei Untersuchungen im Rahmen des Langlands-Programms herauskristallisiert hat.[234]
Beziehung zur Jacobischen Theta-Funktion

Eine sehr wichtige Eigenschaft der Riemannschen Zeta-Funktion ist ihre Funktionalgleichung. Diese drückt sich am einfachsten über
aus und es ist zu bemerken, dass auf der rechten Seite erstaunlicherweise die komplexe Variable einfach durch ersetzt wird.
Es gibt mehrere Herleitungsvarianten zum Auffinden dieser Gleichung. Zwei verschiedene zeigte bereits Riemann. Eine davon schließt einen einfachen Spezialfall der Jacobischen Theta-Funktion
direkt mit ein. Von Vorteil ist die Modifizierung , es gilt . Die Theta-Funktion ist dabei eine Modulform halbganzen Gewichts: Mit der Poissonschen Summenformel fand bereits Jacobi die Identität , woraus sofort folgt.[235]
Ausgangspunkt ist die Integraldarstellung
Der folgende Trick ist eine Standardumformung beim Beweis des Heckeschen Umkehrsatzes. Durch eine Aufspaltung des Integrals in die Intervalle und , wobei in letzteres die Substitution vorgenommen wird,[235] folgt:
Das zweite Integral kann elementar berechnet werden:
Wie man leicht erkennt, ist die rechte Seite unter der Abbildung unverändert, woraus schon die Funktionalgleichung folgt. Diese Argumentation ist gerechtfertigt, weil das Integral auf der rechten Seite nun für alle existiert.[236]
Auftreten in der Wahrscheinlichkeitstheorie, Statistik und probabilistischen Zahlentheorie
Teilerfremde Tupel
Auch einige Wahrscheinlichkeitsgesetze aus der Zahlentheorie stehen in engem Zusammenhang zu der Zeta-Funktion. Ein Satz von Ernesto Cesàro besagt, dass die asymptotische Dichte von Paaren ganzer Zahlen, die teilerfremd sind, gleich
ist, d. h., der Anteil solcher Paare in einem Intervall ganzer Zahlen konvergiert gegen , wenn gegen geht. Dasselbe gilt für die asymptotische Wahrscheinlichkeit, dass eine zufällig gewählte Zahl quadratfrei ist.
Allgemeiner ist die asymptotische Wahrscheinlichkeit, dass positive ganze Zahlen keine -te Potenz größer 1 als gemeinsamen Teiler haben.[237]
Beziehungen zur Theorie der Zufallsmatrizen
Im Jahr 1972 beschrieb der Mathematiker Hugh Montgomery am Princeton Institute for Advanced Studies während einer Teepause einem Kollegen, dem Quantenphysiker Freeman Dyson, sein Modell für die Paarkorrelation von Nullstellen der Zeta-Funktion. Unter Annahme der Riemannschen Vermutung lassen sich die nicht-trivialen Nullstellen mit reellen schreiben. Im Folgenden wird die Normalisierung
betrachtet. Zusammen mit erhält man Als weiteres Vorgehen kann für Zahlen die Paarkorrelation und allgemeiner der lineare Operator für Funktionen
studiert werden. Der folgende Satz von Montgomery, unter Annahme der Riemannschen Vermutung bewiesen, klassifiziert das asymptotische Verhalten der für eine weite Klasse von Funktionen : Hat die Fourier-Transformation von kompakten Träger mit , so folgt[238]
Dyson, einer der Gründer der Theorie der Zufallsmatrizen, erkannte sogleich einen Zusammenhang. Sind nämlich mit die Eigenwerte eines Elementes der unitären Gruppe und wird gesetzt, so folgt wie oben[239]
Hierbei bezeichnet das Haar-Maß auf . Die Ähnlichkeit beider Formeln deutet auf eine starke Verbindung der Theorie der Zeta-Funktion zur Theorie unitärer Zufallsmatrizen hin. Diese Verbindung wird durch das sog. Pólya-Hilbert-Programm unterstrichen: Lassen sich die Werte aller nicht-trivialen Nullstellen als Eigenwerte eines (selbstadjungierten) Hamilton-Operators schreiben, folgt die Riemannsche Vermutung.[240]
Vermutung von Keating-Snaith

Keating und Snaith haben eine Vermutung über das asymptotische Wachstum der Potenzmomente der Zeta-Funktion formuliert. Diese sagt aus, dass für alle gilt:
mit dem arithmetischen Faktor
und dem Matrizen-Faktor
Um den Weg bis zu dieser Vermutung und deren Bezug zur Statistik zu verstehen, ist das folgende sehr heuristische Argument hilfreich. Geht man davon aus, dass alle Primzahlen „unabhängig verteilt“ sind, so folgt mittels Euler-Produkt für den Erwartungswert (bezüglich des Lebesgue-Maßes auf )
und daraus gewinnt man letztlich die von Keating und Snaith gegebenen Terme, wobei der Matrizen-Faktor nur ein Korrekturterm innerhalb dieses „Unabhängigkeitsmodells“ ist.[241][242]
Algorithmen zur schnellen numerischen Berechnung
Für eine schnelle numerische Berechnung der Funktion sind viele klassische Darstellungsformen unbrauchbar. Dazu zählen etwa im Besonderen die Dirichlet-Reihe, das Euler-Produkt, die Darstellung als Mellin-Transformation und das Hadamard-Produkt. Für effiziente Leistung ist ein endlicher approximativer Summenausdruck mit hoher Konvergenzgeschwindigkeit am geeignetsten. Als gute und historisch betrachtet früh verwendete Methode erweist sich die „abgebrochene“ Summenformel, die mit Hilfe der Euler-Maclaurin-Summenformel gewonnen wird. Generell wird zunächst eine beliebige natürliche Zahl festgelegt, für die außerdem gelten sollte. Es gilt dann:[26]
Dabei gilt für das Restglied[243][27]
Bei der (freien) Wahl von ist außerdem zu beachten, dass das Restglied nur auf der Halbebene konvergiert. Daher muss stets gelten. Für größer werdende Werte von verkleinert sich der Fehler demnach rapide.[26] Durch Anwendung der Funktionalgleichung (eine schnelle Berechnung der Gamma-Funktion und der Exponentialfunktion ist leicht zu implementieren), kann zudem ohne Einschränkung angenommen werden. Hier ist die Summenformel deutlich schneller. Ein Nachteil dieser Methode ist aber, dass sie für wachsende Imaginärteile an Effizienz einbüßt.
Ein Verfahren mittels abgebrochener alternierender Reihen stammt von Peter Borwein.[244]
Viele Methoden verlieren jedoch an Präzision, wenn der Imaginärteil des Arguments sehr groß gewählt wird, was bei der Nullstellensuche entlang der kritischen Geraden problematisch ist. Daher greift man hier auf andere Methoden zurück, eine davon ist die Riemann-Siegel-Formel.[245] Im Jahr 1988 entwickelten A. M. Odlyzko und A. Schönhage ein sehr schnelles Verfahren, um Werte der Riemannschen Zeta-Funktion auf der kritischen Geraden zu bestimmen. Es wird als Verfahren von Odlyzko und Schönhage bezeichnet. Dieses basiert auf den Ideen der Riemann-Siegel-Formel, benötigt jedoch nur noch anstatt Rechenoperationen, wobei beliebig klein gewählt werden kann. Die Verfeinerung der Rechentechniken basiert auf der schnellen Fouriertransformation.[246]
Ableitung
In den vergangenen Jahrzehnten wurde auch immer verstärkter über die Eigenschaften der Ableitung geforscht.
Die Funktion besitzt eine holomorphe Fortsetzung auf ganz mit einem Pol zweiter Ordnung in . Auch sie erfüllt eine Funktionalgleichung, welche sich durch beidseitiges Ableiten der gewöhnlichen Funktionalgleichung der Zeta-Funktion ergibt.
Zwar besitzt die Ableitung keine Darstellung als ein Euler-Produkt, jedoch gibt es auch hier Zusammenhänge zu den Primzahlen. Eine solche Formel lässt sich mittels logarithmischer Ableitung gewinnen, also über die Identität
Setzt man hier
für die -te Primzahl, ergibt sich[11][247]
Auch für die Ableitung sind die Nullstellen von zahlentheoretischem Interesse. So ist die Aussage im Streifen äquivalent zur Riemannschen Vermutung.[248] Die reellen Nullstellen im negativen Bereich sind asymptotisch gegeben durch
Dabei ist , und .[249]
Für alle negativen ganzen Zahlen erhält man über die Funktionalgleichung[250][251]
Andere Werte sind
wobei hier die Glaisher-Kinkelin-Konstante bezeichnet.[252]
In Kunst und Kultur
Im Film Die Poesie des Unendlichen ist im Büro von Godfrey Harold Hardy im Hintergrund auf einer Tafel die Euler-Produkt-Entwicklung der Riemannschen Zeta-Funktion angeschrieben.
In Neal Stephensons Roman Cryptonomicon wird die Riemannsche Zeta-Funktion mehrfach in Zusammenhang mit den fiktiven Kryptocodes Azure, Pufferfish und Arethusa erwähnt.[253]
Siehe auch
Literatur
Zur Mathematik
Die Fachliteratur zur Mathematik der Riemannschen Zetafunktion wurde zu einem großen Teil in englischer Sprache verfasst. Es existiert vergleichsweise wenig deutschsprachige Fachliteratur zu diesem Thema. Wegen des engen Zusammenhangs zwischen Riemannscher Zeta-Funktion, Riemannscher Vermutung, Primzahlen und Primzahlsatz behandelt Fachliteratur zu einem der drei zuletzt genannten Themen häufig auch die Riemannsche Zeta-Funktion. Lehrbücher zur analytischen Zahlentheorie enthalten in der Regel eine Darstellung der Riemannschen Zeta-Funktion. Mitunter gilt dies sogar für Lehrbücher zur algebraischen Zahlentheorie.
- Tom M. Apostol: Introduction to Analytic Number Theory. Springer, New York 1976, ISBN 0-387-90163-9 (Insbesondere Kapitel 11, 12 und 13).
- Peter Borwein, Stephen Choi, Brendan Rooney, Andrea Weirathmueller: The Riemann Hypothesis. Springer, New York 2008, ISBN 978-0-387-72125-5 (Insbesondere Kapitel 2 und 3. Fasst in Kapitel 10 die Geschichte der Riemannschen Zeta-Funktion, der Riemannschen Vermutung und des Primzahlsatzes von 1737 bis 2004 zusammen. Gibt zu diesem Themenkreis im zweiten Teil des Buches eine Auswahl der wichtigsten mathematischen Originalarbeiten von 1852 bis 2004 wieder.).
- Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, Berlin/Heidelberg 1995, ISBN 3-540-58821-3.
- Pierre Cartier: An Introduction to Zeta Functions. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson (Hrsg.): From Number Theory to Physics, Springer-Verlag (Second Corrected Printing 1995), Berlin/Heidelberg 1992, ISBN 3-540-53342-7, S. 1–63.
- John Brian Conrey: More than two fifths or the zeros of the Riemann zeta function are on the critical line. In: Journal für die reine und angewandte Mathematik (Crelles Journal). Band 1989, Nr. 399. Walter de Gruyter, Berlin, New York 1989, S. 1–26.
- Bernhard Riemann: Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse (Wikisource). In: Monatsberichte der Königlichen Preußischen Akademie der Wissenschaften zu Berlin. Berlin 1859, S. 671–680.
- Harold Edwards: Riemann’s Zeta Function. Dover, 2001, ISBN 0-486-41740-9 (Dieses Buch erläutert ausführlich die Mathematik in Bernhard Riemanns berühmter Originalarbeit Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse aus dem Jahr 1859. Es enthält im Anhang eine englische Übersetzung dieser Originalarbeit.).
- Aleksandar Ivić: The Riemann Zeta-Function: theory and applications. Dover, Mineola 2003, ISBN 0-486-42813-3.
- Henryk Iwaniec, Emmanuel Kowalski: Analytic Number Theory. American Mathematical Society, Providence 2004, ISBN 0-8218-3633-1 (Insbesondere Kapitel 1 und 5).
- Eugen Jahnke: Tafeln höherer Funktionen. Teubner, Stuttgart 1966.
- Anatoly A. Karatsuba, S. M. Voronin: The Riemann Zeta-Function. Walter de Gruyter, Berlin 1992, ISBN 3-11-013170-6.
- Max Koecher: Klassische elementare Analysis. Birkhäuser Verlag, Basel, Boston 1987, ISBN 3-7643-1824-4 (Insbesondere Kapitel II und VI).
- Peter Meier, Jörn Steuding: Wer die Zetafunktion kennt, kennt die Welt! In: Spektrum der Wissenschaft Dossier 6/2009: „Die größten Rätsel der Mathematik“. ISBN 978-3-941205-34-5, S. 12–19.
- Jürgen Neukirch: Algebraische Zahlentheorie. Springer, Berlin 1992, ISBN 3-540-54273-6 (Insbesondere Kapitel 7).
- Samuel Patterson: An introduction to the theory of the Riemann Zeta-Function. Cambridge University Press, New York 1995, ISBN 0-521-49905-4.
- Paulo Ribenboim: Die Welt der Primzahlen. 2. Auflage. Springer, Berlin/Heidelberg 2011, ISBN 978-3-642-18078-1 (Insbesondere Kapitel 4, Abschnitt I.).
- Atle Selberg: On the zeros of the Riemann zeta-function. In: Skr. Norske Vid. Akad. Oslo. Band 10, 1942, S. 1–59.
- Jörn Steuding: Value-Distribution of L-Functions. Springer, Berlin/Heidelberg 2007, ISBN 3-540-26526-0 (Insbesondere Kapitel 1, das auch den Beweis des Universalitätssatzes von Woronin skizziert.).
- Edward Charles Titchmarsh: The Theory of the Riemann Zeta-Function. 1951.
- Sergei Michailowitsch Woronin: Theorem on the ‘universality’ of the Riemann zeta-function. In: Mathematics of the USSR-Izvestiya. Band 9, Nr. 3, 1975, S. 443–445.
- Don Zagier: Zetafunktionen und quadratische Körper. Springer, Berlin; Heidelberg; New York 1981, ISBN 3-540-10603-0 (Teil 1, insbesondere § 4).
Zur Geschichte
- Peter Borwein et al.: The Riemann Hypothesis. (Siehe geschichtliche Zeitleiste in Kapitel 10. Angaben zum Buch befinden sich in der Literaturliste „Zur Mathematik“.).
- Władysław Narkiewicz: The Development of Prime Number Theory. From Euclid to Hardy and Littlewood. Springer, Berlin 2000, ISBN 3-540-66289-8 (Geschichtlich orientiertes mathematisches Lehrbuch).
- Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 4. Auflage. Beck, München 2005, ISBN 3-406-52320-X.
Weblinks
Deutschsprachige Weblinks:
- Otto Forster: Riemannsche Zetafunktion. Website zur Vorlesung von Otto Forster im Wintersemester 2008/09 am Mathematischen Institut der Ludwig-Maximilians-Universität München, enthält Links zu den einzelnen Kapiteln seines Vorlesungsskripts (PDF-Dokumente).
- Bernhard Schiekel: Zeta-Funktionen in der Physik – eine Einführung. doi:10.18725/OPARU-4418. Umfangreiches Skript über das Auftreten von Zetafunktionen in der Physik, 2011.
Englischsprachige Weblinks:
- Tom Apostol: Zeta and Related Functions. Kapitel 25 der Digital Library of Mathematical Functions (Digitale Bibliothek mathematischer Funktionen) des US-amerikanischen National Institute of Standards and Technology (Nationales Institut für Standards und Technologie).
- Enrico Bombieri: Problems of the Millennium: The Riemann Hypothesis. (PDF; 194 kB). Offizielle Problembeschreibung des Clay Mathematics Institute bzgl. der Riemannschen Vermutung, eines der sieben Millennium-Probleme.
- Xavier Gourdon, Pascal Sebah: The Riemann Zeta-function. (PDF; 68 kB). Definition der Riemannschen Zetafunktion, 2003.
- Xavier Gourdon, Pascal Sebah: The Riemann Zeta-function: Generalities. (PDF; 97 kB). Allgemeine Eigenschaften, 2004.
- Xavier Gourdon, Pascal Sebah: Numerical Evaluation of the Riemann Zeta-function. (PDF; 162 kB). Numerische Berechnungen, 2003.
- Xavier Gourdon, Pascal Sebah: Distribution of the zeros of the Riemann Zeta function. (PDF; 112 kB). Verteilung der Nullstellen, 2004.
Mathematische Fachartikel:
- P. Cerone: Bounds for Zeta and Related Functions. (PDF;248 kB). Journal of Inequalities in Pure and Applied Mathematics, Band 6, Nr. 5, 2005 (enthält Abschätzungen der Zetafunktion für ungerade ).
Einzelnachweise
- ↑ Barkley Rosser: Explicit bounds for some functions of prime numbers. In: American Journal of Mathematics. 63. Jahrgang, Nr. 1, 1941, S. 211–232, doi:10.2307/2371291.
- ↑ E. Freitag, R. Busam: Funktionentheorie 1, Springer; Auflage: 4. Aufl. 2006, ISBN 978-3-540-31764-7, S. 440
- ↑ vgl. Arpita Kar, M. Ram Murty: The Central Limit Theorem in Algebra and Number Theory, In: B. Ramakrishnan, Bernhard Heim, Brundaban Sahu (edt.): Modular Forms and Related Topics in Number Theory, S. 101.
- ↑ Carl Friedrich Gauss Werke, Zweiter Band, Herausgegeben von der königlichen Gesellschaft der Wissenschaften zu Göttingen, 1863, S. 444–447 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Miller, Gary L. (1976), Riemann’s Hypothesis and Tests for Primality, Journal of Computer and System Sciences, 13 (3): 300–317, doi:10.1145/800116.803773
- ↑ a b E. Freitag, R. Busam: Funktionentheorie 1, Springer; Auflage: 4. Aufl. 2006, ISBN 978-3-540-31764-7, S. 432.
- ↑ P. Bourgade, J. P. Keating, : Quantum chaos, random matrix theory, and the Riemann ζ-function, Séminaire Poincaré XIV (2010), 115 – 153, S. 116
- ↑ Jonathan M. Borwein, David M. Bradley, Richard E. Crandall: Computational strategies for the Riemann zeta function. Journal of Computational and Applied Mathematics 121 (2000) 247–296, (PDF).
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1992, ISBN 2-540-54273-5, S. 440.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A Tricentennial Tribute. S. 36.
- ↑ a b E. Freitag, R. Busam: Funktionentheorie 1, Springer; Auflage: 4. Aufl. 2006, S. 433
- ↑ Hugh L. Montgomery, Robert C. Vaughan: Multiplicative Number Theory I. Classical Theory, Cambridge studies in advanced mathematics, S. 185.
- ↑ Hugh L. Montgomery, Robert C. Vaughan: Multiplicative Number Theory I. Classical Theory, Cambridge studies in advanced mathematics, S. 328.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, ISBN 978-3-540-48495-0, S. 74.
- ↑ Komaravolu Chandrasekharan: Einführung in die analytische Zahlentheorie. Springer Verlag, 1965/66, Kapitel XI, S. 2.
- ↑ Carl-Erik Fröberg: On the prime zeta function. In: Nordisk Tidskr. Informationsbehandling (BIT). 8. Jahrgang, Nr. 3, 1968, S. 187–202, doi:10.1007/BF01933420.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 209.
- ↑ T. M. Apostol: Introduction to Analytic Number Theory. Springer-Verlag, New York / Heidelberg / Berlin 1976, S. 251.
- ↑ Aleksandar Ivic: The Riemann Zeta-Function. Dover, ISBN 978-0-486-42813-0, S. 4.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 232.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 232.
- ↑ Helmut Hasse: Ein Summierungsverfahren für die Riemannsche ζ-Reihe. Mathematische Zeitschrift. 32 (1): 458–464 (1930). doi:10.1007/BF01194645.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen, 5. Auflage, Springer, S. 484.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen, 5. Auflage, Springer, S. 509.
- ↑ Hans Rademacher: Topics in Analytic Number Theory. Springer-Verlag, Berlin et al. 1973, ISBN 3-540-05447-2.
- ↑ a b c d H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 114.
- ↑ a b H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 115.
- ↑ Jörn Steuding: On the Universality of the Riemann zeta-function. (PDF; 456 kB), 11. Oktober 2012, S. 3.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 233.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, ISBN 978-3-540-48495-0, S. 288–290.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 74, Setzen von in die zweite Formel.
- ↑ H. Hasse: "Ein Summierungsverfahren für die Riemannsche ζ-Reihe", Mathematische Zeitschrift. 32 (1) (1930): 458–464, doi:10.1007/BF01194645.
- ↑ Jonathan M. Borwein, David M. Bradley, Richard E. Crandall: Computational strategies for the Riemann zeta function. Journal of Computational and Applied Mathematics 121 (2000) 247–296, (PDF), S. 253.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, ISBN 978-3-540-48495-0, S. 50.
- ↑ Raymond Ayoub: Euler and the zeta function. In: Amer. Math. Monthly. 81. Jahrgang, 1974, S. 1067–86, doi:10.2307/2319041 (maa.org).
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, ISBN 978-3-540-48495-0, S. 53.
- ↑ L. Euler: Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum, Teil II, Kapitel 5, S. 337 ff. (PDF)
- ↑ Raymond Ayoub: Euler and the zeta function. In: Amer. Math. Monthly. 81. Jahrgang, 1974, S. 1078, doi:10.2307/2319041 (maa.org).
- ↑ A. Schmidt: Einführung in die algebraische Zahlentheorie. Springer, Berlin / Heidelberg / New York, ISBN 978-3-540-45973-6, S. 144.
- ↑ Leonhard Euler: Variae observationes circa series infinitas. 25. April 1737, Commentarii academiae scientiarum imperialis Petropolitanae 9, 1744, S. 160–188 (lateinisch; Euler-Produkt als „Theorema 8“ auf S. 174 f.). Deutsche Übersetzung (PDF) von Alexander Aycock.
- ↑ Leonhard Euler: Variae observationes circa series infinitas. 25. April 1737, Commentarii academiae scientiarum imperialis Petropolitanae 9, 1744, S. 160–188 (lateinisch; Euler-Produkt als „Corollarium 1“ auf S. 176 f.). Deutsche Übersetzung (PDF) von Alexander Aycock.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover Verlag ISBN 978-0-486-41740-0, S. 1.
- ↑ F. Diamond, J. Shurman: A first course in modular forms. Springer, ISBN 978-0-387-23229-4, S. 124.
- ↑ L. Euler: Remarques sur un beau rapport entre les series des puissances tant directes que reciproques. Ursprünglich veröffentlicht in Memoires de l’academie des sciences de Berlin 17, 1768, S. 83–106 (Opera Omnia: Reihe 1, Bd. 15, S. 70–90 (PDF).
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 100
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Deutscher Taschenbuch Verlag, ISBN 978-3-423-34299-5, S. 192
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 188.
- ↑ Laugwitz, Bernhard Riemann, Birkhäuser 1996, S. 180
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 189.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 129
- ↑ H. von Mangoldt: Zu Riemanns Abhandlung „Über die Anzahl der Primzahlen unter einer gegebenen Größe“, J. Reine Angew. Math. 114 (1895), S. 255.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 39.
- ↑ H. von Mangoldt: Zu Riemanns Abhandlung „Über die Anzahl der Primzahlen unter einer gegebenen Größe“, J. Reine Angew. Math. 114 (1895), S. 255–305.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 61.
- ↑ Władysław Narkiewicz: The Development in Prime Number Theory, Springer Monographs in Mathematics, S. 183.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, ISBN 978-3-540-48495-0, S. 216.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, ISBN 978-3-540-48495-0, S. 216–217.
- ↑ A. E. Ingham: The Distribution of Prime Numbers, Cambridge University Press.
- ↑ Joel Spencer, Ronald Graham: The Elementary Proof of the Prime Number Theorem. Mathematical Intelligencer 2009, Nr. 3.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, ISBN 978-3-540-48495-0, S. 216–217.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 12.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, ISBN 978-3-540-48495-0, S. 244–245.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, ISBN 978-3-540-48495-0, S. 245.
- ↑ Brief von Hardy an Ramanujan vom 26. März 1913. Nach Bruce Berndt, Robert Rankin: Ramanujan, Letters and Commentary. AMS S. 77.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 174.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 170 ff.
- ↑ Bruce C. Berndt: Ramanujan’s Notebooks Part I, Springer Verlag, S. 125.
- ↑ Bruce C. Berndt: Ramanujan's Notebooks Part I, Springer Verlag, S. 128.
- ↑ G. E. Andrews, B. C. Berndt: Ramanujan’s Lost Notebook. Part IV. Springer, 2013, ISBN 978-1-4614-4080-2, S. 191.
- ↑ Bruce C. Berndt: Ramanujan’s Notebooks Part I, Springer Verlag, S. 163–164.
- ↑ Bruce C. Berndt: Ramanujan’s Notebooks Part II, Springer Verlag, S. 276
- ↑ G. E. Andrews, B. C. Berndt: Ramanujan’s Lost Notebook. Part IV. Springer, 2013, ISBN 978-1-4614-4080-2, S. 239.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 166.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 130.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 136.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 192.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 136.
- ↑ Calculations relating to the zeros. Kapitel 15. In: Titchmarsh: The Theory of the Riemann Zeta function.
- ↑ A. Odlyzko: Analytic computations in number theory, Proc. Symp. Appl. Math. 48 (1994) 441–463.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 234
- ↑ Turing, Alan M. (1953), Some calculations of the Riemann zeta-function, Proceedings of the London Mathematical Society, Third Series, 3: 99–117
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 238.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 268.
- ↑ Ed Pegg Jr.: «Ten Trillion Zeta Zeros».
- ↑ Gourdon, Xavier (2004): The first zeros of the Riemann Zeta function, and zeros computation at very large height (PDF)
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 323.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 323–324.
- ↑ Odlyzko, A. M. (1987), On the distribution of spacings between zeros of the zeta function, Mathematics of Computation, 48 (177): 273–308, doi:10.2307/2007890
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 346.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 349.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 347–349.
- ↑ Offizielle Liste der Millennium-Probleme: The Millennium Prize Problems, abgerufen am 30. Dezember 2019
- ↑ G. L. Miller: Riemann’s hypothesis and tests for primality, Journal of Computer and System Sciences 13 (1976), 300–317, doi:10.1145/800116.803773
- ↑ M. O. Rabin: Probabilistic algorithm for testing primality, Journal of Number Theory (1980), 12 (1): 128–138, doi:10.1016/0022-314X(80)90084-0
- ↑ Bernhard Schiekel: Zeta-Funktionen in der Physik - eine Einführung, (PDF), abgerufen am 1. Januar 2020.
- ↑ E. Elizalde u. a., Zeta Regularization Techniques with Applications, World Scientific, 1994
- ↑ Ruggiero, Zimerman; Villani (1977): Application of Analytic Regularization to the Casimir Forces, Revista Brasileira de Física. 7 (3), (PDF).
- ↑ siehe John Baez: This Week’s Finds in Mathematical Physics (Week 126). 1998.
- ↑ Henri Guiter, Michail V. Arapov (Hrsg.): Studies on Zipf’s Law (= Quantitative Linguistics. Bd. 16). Studienverlag Brockmeyer, Bochum 1982, ISBN 3-88339-244-8.
- ↑ Eric W. Weisstein: Zipf distribution. In: MathWorld (englisch).
- ↑ T. M. Apostol: Introduction to Analytic Number Theory. Springer-Verlag, New York / Heidelberg / Berlin 1976, S. 259.
- ↑ Aleksandar Ivic: The Riemann Zeta-Function. Dover, ISBN 978-0-486-42813-0, S. 4.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, ISBN 978-3-540-48495-0, S. 290.
- ↑ T. M. Apostol: Introduction to Analytic Number Theory. Springer-Verlag, New York / Heidelberg / Berlin 1976, S. 260.
- ↑ B. Riemann: Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse. In: Monatsberichte der Königlichen Preußischen Akademie der Wissenschaften zu Berlin. Berlin 1859, S. 673.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 16.
- ↑ Hardy, Divergent Series, Clarendon Press 1949, Kapitel 2
- ↑ Ayoub, Euler and the Zetafunction, American Mathematical Monthly, Band 81, Dezember 1974, S. 1067–1086
- ↑ Zitiert nach Detlef Laugwitz, Bernhard Riemann (1826–1866), Birkhäuser 1996, S. 175.
- ↑ H. Hamburger: Über die Riemannsche Funktionalgleichung der Zeta-Funktion. Math. Zeit. 10 (1921), S. 240–254.
- ↑ O. Hölder: Über die Eigenschaft der Gamma Funktion keiner algebraische Differentiagleichung zu genügen, Math. Ann., 28 (1887) 1-13.
- ↑ V. E. E. Stadigh: Ein Satz über Funktionen, die algebraische Differentialgleichungen befriedigen, und über die Eigenschaft der Funktion keiner solchen Gleichung zu genügen, 1902, (Archiv), S. 32.
- ↑ Dragan Miličić: Notes on Riemann’s Zeta Function. (PDF; 121 kB).
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 76 u. 80.
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 78.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 240.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 212.
- ↑ A. Laforgia und P. Natalini: Turan-type inequalities for some special functions, Journal of inequalities in Pure and Applied Mathematics, Volume 7, Issue 1, Article 32, 2006.
- ↑ T. M. Apostol: Modular Functions and Dirichlet Series in Number Theory. Springer-Verlag, New York 1990. ISBN 0-387-90185-X, S. 155.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 200.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 262.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 91.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 251.
- ↑ T. M. Apostol: Introduction to Analytic Number Theory. Springer-Verlag, New York / Heidelberg / Berlin 1976, S. 266.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 234.
- ↑ Roger Apéry: Irrationalité de et . Astérisque 61, 1979, S. 11–13.
- ↑ B. Riemann: Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse. In: Monatsberichte der Königlichen Preußischen Akademie der Wissenschaften zu Berlin. Berlin 1859, S. 674.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 19.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 244–245.
- ↑ a b Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 252.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 159.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 271.
- ↑ J. B. Conrey, A. Ghosh und S. M. Gonek: Simple Zeros of the Riemann Zeta‐Function, Proceedings of the London Mathematical Society, Volume 76, Issue 3, S. 497–522.
- ↑ H. M. Bui und D. R. Heath-Brown: On simple zeros of the Riemann zeta function, Bulletin of the London Mathematical Society, Volume 45, Issue 5, October 2013, Pages 953–961, doi:10.1112/blms/bdt026
- ↑ J. Steuding: On simple zeros of the Riemann zeta-function (PDF), Dissertation an der Universität Hannover, 1999.
- ↑ G.H. Hardy und J.E. Littlewood: The zeros of Riemann’s zeta-function on the critical line, Math. Z. 10 (3–4), (1921), S. 283–317. doi:10.1007/bf01211614
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 257.
- ↑ F. Mertens: Ueber eine Eigenschaft der Riemann’schen ζ-Function. Wien 1898, S. 1429–1434.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 249.
- ↑ H. J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, ISBN 3-540-58821-3, S. 99 ff.
- ↑ K. Ford: Vinogradov’s integral and bounds for the Riemann zeta function. In: Proc. London Math. Soc. 85. Jahrgang, Nr. 3, 2002, S. 565–633, doi:10.1112/S0024611502013655.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 250.
- ↑ W. Ellison, M. Mendès France: Les nombres premiers. Hermann, 1975.
- ↑ K. Ford: Vinogradov’s integral and bounds for the Riemann zeta function. Proc. London Math. Soc. 85, 565–633 (2002).
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 459.
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1992, ISBN 2-540-54273-5, S. 453.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 271.
- ↑ Schoenfeld, Lowell (1976): Sharper bounds for the Chebyshev functions and . II. Mathematics of Computation, 30 (134): 337–360, Corollary 1, (PDF).
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 200.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 226–229.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 226.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 265.
- ↑ Norman Levinson: At least One-Third of Zeros of Riemann’s Zeta-Function are on . (PDF; 314 kB).
- ↑ J. B. Conrey: More than two fifths of the zeros of the Riemann zeta function are on the critical line. J. Reine Angew. Math. 399 (1989).
- ↑ Andrew Odlyzko: Table of zeros of the Riemann zeta function.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, ISBN 978-3-540-48495-0, S. 226.
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 80.
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 86.
- ↑ André Voros: More Zeta Functions for the Riemann Zeros. (PDF; 182 kB), CEA, Service de Physique Théorique de Saclay (CNRS URA 2306), S. 6.
- ↑ J. Steuding: Universality of L-Functions. (PDF; 159 kB). In: pdfs.semanticscholar.org. Departamento de Matemáticas, Universidad Autónoma de Madrid. Göttingen 2004.
- ↑ R. Garunkštis, A. Laurinčikas, K. Matsumoto, J. Steuding, R. Steuding: Effective uniform approximation by the Riemann zeta-function. In: Publicacions Matemàtiques, Bd. 54, 2010, S. 210.
- ↑ E. C. Titchmarsh, D. R. Heath-Brown: The Theory of the Riemann Zeta-function. Zweite Auflage. Oxford U. P., Oxford 1986, ISBN 0-19-853369-1, S. 308–309.
- ↑ J. Steuding: Universality of L-Functions. (PDF; 159 kB). In: pdfs.semanticscholar.org. Departamento de Matemáticas, Universidad Autónoma de Madrid. Göttingen 2004.
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 117.
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 117–119.
- ↑ C. L. Siegel: Über Riemanns Nachlaß zur analytischen Zahlentheorie. Quellen u. Studien z. Geschichte der Math. Astr. u. Physik, Abt. B: Studien, 2 (1932), 45–80.
- ↑ I. M. Vinogradov: A new estimate for ζ(1 + it), Izv. Akad. Nauk SSSR, Ser. Mat. 22 (1958), 161–164. (PDF) (auf Russisch)
- ↑ N. M. Korobov: Estimates of trigonometric sums and their applications, Uspekhi Mat. Nauk, 1958, Volume 13, Issue 4(82), 185–192 (PDF) (auf Russisch)
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 252.
- ↑ H.-E. Richert, Zur Abschätzung der Riemannschen Zetafunktion in der Nähe der Vertikalen σ = 1, Math. Annalen 169 (1967), 97–101.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 252.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 253.
- ↑ a b J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 126.
- ↑ a b c J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 127.
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 151.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 188.
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer, Berlin/Heidelberg 1995, S. 150.
- ↑ Aleksandar Ivić: The Riemann Zeta-Function: theory and applications. Dover (Mineola), 2003, S. 129.
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer, Berlin/Heidelberg 1995, S. 151.
- ↑ J. B. Conrey und S. M. Gonek: High moments of the Riemann zeta-function. In: Duke Methematical Journal, Bd. 107, Nr. 3 (2001), S. 577–604.
- ↑ D. R. Heath-Brown: Fractional Moments of the Riemann Zeta-Function. In: Journal of the London Mathematical Society, Bd. s2–24, Nr. 1, August 1981, S. 65–78, (doi:10.1112/jlms/s2-24.1.65).
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 130.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 188.
- ↑ R. Backlund: Über die Beziehung zwischen Anwachsen und Nullstellen der Zeta-Funktion, Ofversigt Finska Vetensk. Soc. 61, No. 9, (1918-1919).
- ↑ E.C. Titchmarsh: The theory of the Riemann zeta-function, Oxford University Press, New York, 1986.
- ↑ K. Soundararajan: Moments of the Riemann zeta-function. In: Annals of Mathematics, 2. Reihe, Bd. 170, Nr. 2.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory, AMS, 1990, S. 350.
- ↑ J. Korevaar: Tauberian Theory. A century of developments. Grundlehren der mathematischen Wissenschaften, Springer-Verlag, Berlin Heidelberg New York, ISBN 3-540-21058-X, S. 124.
- ↑ J. Korevaar: Tauberian Theory. A century of developments. Grundlehren der mathematischen Wissenschaften, Springer-Verlag, Berlin Heidelberg New York, ISBN 3-540-21058-X, S. 133–135.
- ↑ D. Zagier: Newman's short proof of the prime number theorem. In: The American Mathematical Monthly, Bd. 104, Nr. 8 (Oktober 1997), S. 705–708 (PDF).
- ↑ J. Laurie Snell, Bill Peterson, Jeanne Albert, Charles Grinstead: Chance in the Primes. Chapter 1. ( des vom 15. Juni 2013 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 33 und 48.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 34.
- ↑ B. Riemann: Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse. In: Monatsberichte der Königlichen Preußischen Akademie der Wissenschaften zu Berlin. Berlin 1859, S. 674.
- ↑ Eric W. Weisstein: Riemann Prime Counting Function. In: MathWorld (englisch).
- ↑ J. E. Littlewood: Sur la distribution des nombres premiers. C. R. Acad. Sci. Paris 158, 1869–1872, (1914).
- ↑ Tadej Kotnik: The prime-counting function and its analytic approximations, Adv Comput Math (2008) 29:55–70, doi:10.1007/s10444-007-9039-2, (PDF).
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 281.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, Rhode Island 1990, S. 282.
- ↑ J. G. van der Corput: Verschärfung der Abschätzung beim Teilerproblem. In: Math. Ann. 87 (1922) 39–65. Berichtigungen 89 (1923) S. 160.
- ↑ M. N. Huxley: Exponential Sums and Lattice Points III. In: Proc. London Math. Soc. Band 87, Nr. 3, 2003, S. 591–609.
- ↑ G. H. Hardy: On Dirichlet’s divisor problem. In: Lond. M. S. Proc. (2) 15 (1915) 1–25.
Vgl. G. H. Hardy, E. M. Wright: An Introduction to the Theory of Numbers. 4. Auflage, Oxford University Press, Oxford 1975. ISBN 0-19-853310-1, S. 272. - ↑ a b J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 133.
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 132.
- ↑ J. Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin/Heidelberg 1995, S. 136.
- ↑ L. Kalmár: Über die mittlere Anzahl der Produktdarstellungen der Zahlen, Acta Sci. Math. (Szeged) 5:2-2(1930-32), 95-107, S. 96.
- ↑ S. R. Finch: Mathematical Constants, Encyclopedia of Mathematics and its Applications 94, Cambridge University Press, 2003, S. 292.
- ↑ R. Warlimont: Factorisatio Numerorum with Constraints, Journal of Number Theory, Volume 45, Issue 2, October 1993, 186-199.
- ↑ Holger Reeker: Eulerprodukte von zwei-variablen Zetafunktionen. S. 44–46.
- ↑ N. I. Koblitz: Introduction to Elliptic Curves and Modular Forms, Springer-Verlag New York, ISBN 978-0-387-97966-3, S. 79.
- ↑ N. I. Koblitz: Introduction to Elliptic Curves and Modular Forms, Springer-Verlag New York, ISBN 978-0-387-97966-3, S. 90.
- ↑ N. I. Koblitz: Introduction to Elliptic Curves and Modular Forms, Springer-Verlag New York, ISBN 978-0-387-97966-3, S. 221.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 115.
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1992, ISBN 2-540-54273-5, S. 6.
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1992, ISBN 2-540-54273-5, S. 18.
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1992, ISBN 2-540-54273-5, S. 478.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 217.
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1992, ISBN 2-540-54273-5, S. 488.
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1992, ISBN 2-540-54273-5, S. 36 ff.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 217.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 219.
- ↑ Godfrey Harold Hardy, E. M. Wright: Einführung in die Zahlentheorie. R. Oldenbourg, München 1958, S. 292.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 233.
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1992, ISBN 2-540-54273-5, S. 490 ff.
- ↑ M. R. Murty, V. K. Murty: Non-vanishing of L-Functions and Applications, Birkhäuser Basel, ISBN 978-3-0348-0273-4, doi:10.1007/978-3-0348-0274-1, S. 30.
- ↑ M. R. Murty, V. K. Murty: Non-vanishing of L-Functions and Applications, Birkhäuser Basel, ISBN 978-3-0348-0273-4, doi:10.1007/978-3-0348-0274-1, S. 32.
- ↑ J. H. Brunier, G. van der Geer, G. Harder, D. Zagier: The 1-2-3 of Modular Forms, Lectures at a Summer School in Nordfjordeid, Norway, Springer-Verlag Berlin Heidelberg, ISBN 978-3-540-74117-6, doi:10.1007/978-3-540-74119-0, S. 14
- ↑ J. H. Brunier, G. van der Geer, G. Harder, D. Zagier: The 1-2-3 of Modular Forms, Lectures at a Summer School in Nordfjordeid, Norway, Springer-Verlag Berlin Heidelberg, ISBN 978-3-540-74117-6, doi:10.1007/978-3-540-74119-0, S. 18.
- ↑ F. Beukers: Irrationality proofs using modular forms. In: Astérisque. 147.148 (1987), S. 271–283, (PDF).
- ↑ F. Beukers: Irrationality proofs using modular forms. In: Astérisque. 147.148 (1987), S. 271–283, (PDF), Theoreme 4 und 5.
- ↑ F. Beukers: Irrationality proofs using modular forms. In: Astérisque. 147.148 (1987), S. 271–283, (PDF).
- ↑ D. Bump: Automorphic Forms and Representations. Cambridge Studies in Advanced Mathematics 55, ISBN 0-521-65818-7, S. 69.
- ↑ D. Bump: Automorphic Forms and Representations. Cambridge Studies in Advanced Mathematics 55, ISBN 0-521-65818-7, S. 68.
- ↑ D. Bump: Automorphic Forms and Representations. Cambridge Studies in Advanced Mathematics 55, ISBN 0-521-65818-7, S. 65 ff.
- ↑ a b H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 15.
- ↑ Otto Forster: Funktionalgleichung der Zeta-Funktion. (PDF; 251 kB).
- ↑ ITEM 53 (Salamin). In: M. Beeler, R. W. Gosper, R. Schroeppel: HAKMEM. MIT AI Memo 239, 29. Februar 1972 (englisch).
- ↑ P. Bourgade, J. P. Keating, : Quantum chaos, random matrix theory, and the Riemann ζ-function, Séminaire Poincaré XIV (2010), 115 – 153, S. 126.
- ↑ P. Bourgade, M. Yor: Random Matrices and the Riemann zeta function, hal-00119410, 2006, (PDF), S. 4.
- ↑ C. M. Bender, D. C. Brody, Markus P. Müller: Hamiltonian for the zeros of the Riemann zeta function, (arXiv).
- ↑ P. Bourgade, M. Yor: Random Matrices and the Riemann zeta function, hal-00119410, 2006, (PDF), S. 6–7.
- ↑ J. P. Keating und N. C. Snaith: Random Matrix Theory and , Comm. Math. Phys. 214, 2000, S. 57–89.
- ↑ R. Backlund: Uber die Nullstellen der Riemannschen Zetafunktion. Dissertation, Helsinki 1916.
- ↑ P. Borwein: An efficient algorithm for the Riemann zeta function. In: Théra, Michel A. (Hrsg.): Constructive, Experimental, and Nonlinear Analysis (PDF) (= Canadian Mathematical Society Conference Proceedings, Bd. 27). Providence, Rhode Island, 2000, ISBN 978-0-8218-2167-1, S. 29–34.
- ↑ H. M. Edwards: Riemann’s Zeta Function. Dover, ISBN 978-0-486-41740-0, S. 154.
- ↑ A. M. Odlyzko and A. Schoenhage: Fast algorithms for multiple evaluations of the Riemann zeta function. Trans. Am. Math. Soc., 309 (1988), S. 797–809.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 251.
- ↑ N. Levinson, H. Montgomery: Zeros of the derivatives of the Riemann Zeta function, Acta Mathematica, 1974.
- ↑ Bejoy, K. Choudhury: The Riemann zeta-function and its derivatives, Proc. R. Soc. Lond. A (1995), 450, 477-499, doi:10.1098/rspa.1995.0096, (PDF).
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 260.
- ↑ S. R. Finch: Mathematical Constants, Encyclopedia of Mathematics and its Applications 94, Cambridge University Press, 2003, S. 137.
- ↑ S. R. Finch: Mathematical Constants, Encyclopedia of Mathematics and its Applications 94, Cambridge University Press, 2003, S. 135.
- ↑ Neal Stephenson: Cryptonomicon. München, ISBN 3-442-54529-3, S. 22 und S. 770.
Auf dieser Seite verwendete Medien
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
The function z^(11/2)/(e^z - 1) together with a Hankel contour with radius r=3. x = Re(z), y = Im(z).
The Riemann zeta-function on the strip 1/2<Re(s)<1, 103<Im(s)<109, to illustrate Voronin's universality theorem.
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
The Dirichlet series only converges on the half plane Re(s) > 1. By Euler-MacLaurin summation one obtains inductively expressions valid for Re(s) > 1 - q, where q = 1,2,3... This leads to a meromorphic continuation on C.
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
Plot of Polylogarithm Li_{-2}(z).
Autor/Urheber: User:LoStrangolatore, Lizenz: CC BY-SA 3.0
Zero-free region for the Riemann_zeta_function
Plot der Funktion Zeta(x)Gamma(x/2)Exp[-xLog[Pi]/2]
Autor/Urheber: J. Laurie Snell, Lizenz: GPLv2
Approximation of the prime number function in the interval [200, 230] using the first 500 zeros.
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
Plot of the convex Lindelöf Mu function (red = conjectured, smaller than blue in 0 < x < 1).
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
Plot of the summatory function of all multiplicative components against Kalmar's estimate 0.318173*x^(1.72864).
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
Primzahlfunktion mit der Riemannschen R-Funktion.
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
The function z^5/(e^z - 1). The Hankel contour reduces to a circle in this case. x = Re(z), y = Im(z).
Peter Gustav Lejeune Dirichlet
function Riemann Xi function in the complex plane
Der deutsche Mathematiker David Hilbert im Jahr 1886
Photographie von Godfrey Harold Hardy (1877-1947) in seiner Blütezeit.
"Um so sitzen zu können, muß man in einer Public School erzogen worden sein." [Public School = privates Internat].
Quelle unbekannt. Siehe auch: Robert Kanigel: Der das Unendliche Kannte. Das Leben des genialen Mathematikers Srinivasa Ramanujan. Vieweg, 2.Aufl.1995, S.240.A page with explicit results in Euler's original publication De Summis Serierum Reciprocarum.
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 3.0
Schaubild der Funktionen pi(x), Li(x) und R(x) im Intervall 0 bis 350.
Autor/Urheber: , Lizenz: Bild-frei
(full) complex graph of the riemann zeta function
Autor/Urheber: , Lizenz: Bild-frei
complex graph of the Riemann zeta function (Dirichlet series)
Autor/Urheber: Geek3, Lizenz: CC BY-SA 3.0
Riemann-Zeta-function
real and imaginary part on the critical line from 0 to 100.
note that andAutor/Urheber: Taken by Flickr user ioerror, Jacob Appelbaum, Lizenz: CC BY-SA 2.0
Photo from Long Now Seminar, San Francisco, October 05, 2005
Photograph of the Finnish mathematician Ernst Lindelöf (1870–1946).
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
Plot of summatory function of the divisor function against xlog(x) + (2gamma-1)x.
Autor/Urheber: Renate Schmid, Lizenz: CC BY-SA 2.0 de
Hugh L. Montgomery at Workshop: Analytic Number Theory in Oberwolfach, 2008
function Zeta[z] in the complex plane (horizontal axis = Re(z) and vertical axis = Im(z))
Bernhard Riemann's article concerning the number of primes that are less than a given magnitude.
Carl Jacobi (1804-1851). Carl Gustav Jacob Jacobi was not only a great German mathematician but also considered by many as the most inspiring teacher of his time
Richard Dedekind
Illustration of Voronin's universality theorem about the zeta-function in complex analysis
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
Die Primzahlfunktion in großer Skala.
Graph der Riemannschen Zeta-Funktion im Reellen.
Autor/Urheber: historicair 12:01, 6 September 2007 (UTC), Lizenz: CC BY-SA 3.0
Right triangle
Autor/Urheber: Geek3, Lizenz: CC BY 3.0
Plot of the Riemann zeta function on the real axis in the interval [-15,8], where the first trivial zeros can be seen.
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
The function |Zeta(2+it)| for 0 < t < 1000. One can see that it is bounded between Zeta(4)/Zeta(2) and Zeta(2).
Autor/Urheber: Jacobs, Konrad, Lizenz: CC BY-SA 2.0 de
Carl Ludwig Siegel, German mathematician, at Gottingen in 1975.
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
Primzahlfunktion mit der Riemannschen R-Funktion und dem Korrekturterm über die ersten 50 Nullstellenpaare.