Regelmäßiges Polygon
Ein regelmäßiges Polygon, reguläres Polygon, regelmäßiges Vieleck, reguläres Vieleck oder Isogon (von griechisch ἴσος, gleich und γωνία, Winkel) ist in der Geometrie ein ebenes Polygon, das sowohl gleichseitig als auch gleichwinklig ist. Bei einem regelmäßigen Polygon sind demnach alle Seiten gleich lang und alle Innenwinkel gleich groß. Die Ecken eines regelmäßigen Polygons liegen alle auf einem gemeinsamen virtuellen oder realen Kreis, wobei benachbarte Ecken unter dem gleichen Mittelpunktswinkel erscheinen.
Regelmäßige Polygone können einfach oder überschlagen sein. Einfache regelmäßige Polygone sind stets konvex. Überschlagene regelmäßige Polygone lassen sich in einem Zug zeichnen und werden als reguläre Sternpolygone bezeichnet. Die Symmetriegruppe eines regelmäßigen -Ecks ist die Diedergruppe , bestehend aus genau Drehungen und Spiegelungen.
Alle Kenngrößen regelmäßiger Polygone, wie die Länge der Diagonalen, der Umfang oder der Flächeninhalt, können mit Hilfe trigonometrischer Funktionen angegeben werden. Nicht alle regelmäßigen Polygone sind jedoch mit Zirkel und Lineal konstruierbar. Regelmäßige Polygone werden unter anderem bei der Näherung der Kreiszahl , für Parkettierungen, in der Architektur und als Münzform verwendet.
Definition
Ein Polygon mit den Seiten und den Innenwinkeln heißt regelmäßig, wenn
- und
gilt. In einem regelmäßigen Polygon sind demnach alle Seiten zueinander kongruent und alle Winkel gleich groß.[1]
Klassifikation
Man unterscheidet einfache und überschlagene regelmäßige Polygone. Alle einfachen regelmäßigen Polygone mit gleich viel Ecken sind zueinander ähnlich und werden in der kombinatorischen Geometrie mit dem Schläfli-Symbol bezeichnet. Um degenerierte Fälle auszuschließen, wird in der Regel angenommen. Die ersten vier einfachen regelmäßigen Polygone sind:[1]
- das gleichseitige Dreieck ,
- das Quadrat ,
- das regelmäßige Fünfeck und
- das regelmäßige Sechseck .
Reguläre Sternpolygone weisen neben dem geschlossenen Polygonzug, auch eine größere Vielfalt an Formen auf. Sie werden mit dem Schläfli-Symbol bezeichnet, wobei die Umlaufzahl des Polygons um seinen Mittelpunkt angibt. Die Umlaufzahl muss dabei teilerfremd zu sein, ansonsten entartet das Polygon. Die ersten drei regelmäßigen Sternpolygone sind:
- der Fünfstern ,
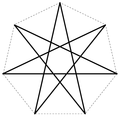
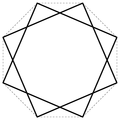
- die Siebensterne und sowie
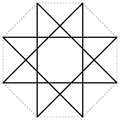
- der Achtstern .
Die Anzahl der verschiedenen Typen regelmäßiger Polygone mit Ecken ist demnach , wobei die eulersche Phi-Funktion ist. Sind und nicht teilerfremd, werden mit dem Schläfli-Symbol Sterne bezeichnet, die aus mehreren regelmäßigen Polygonen zusammengesetzt sind. Beispiele sind das Hexagramm und das Oktagramm .

Kenngrößen
Winkel

Die Ecken eines regelmäßigen Polygons liegen konzyklisch auf einem gemeinsamen Kreis. Ein regelmäßiges Polygon ist damit ein Sehnenvieleck und besitzt so einen Umkreis mit Umkreisradius . Zudem liegen die Ecken gleichabständig auf dem Kreis, das heißt, nebeneinander liegende Ecken erscheinen unter dem gleichen Mittelpunktswinkel (Zentriwinkel)
- .
Damit ist ein regelmäßiges Polygon auch ein Tangentenvieleck mit einem Inkreis mit Inkreisradius . Der Inkreis berührt die Polygonseiten dabei in den Seitenmittelpunkten. Der Inkreismittelpunkt stimmt mit dem Umkreismittelpunkt überein und wird der Mittelpunkt des Polygons genannt. Nachdem die Winkelsumme in einem einfachen -Eck stets ergibt, messen in einem einfachen regelmäßigen Polygon alle Innenwinkel
- .
Da sich an den Ecken eines Polygons Innen- und Außenwinkel zu ergänzen, sind in einem einfachen regelmäßigen Polygon auch alle Außenwinkel gleich groß und messen jeweils[1]
- .
Für die Winkel in regelmäßigen Polygonen ergeben sich beispielsweise folgende Werte:
| Polygon | Mittelpunktswinkel | Innenwinkel | Außenwinkel | |||
|---|---|---|---|---|---|---|
| Gradmaß | Bogenmaß | Gradmaß | Bogenmaß | Gradmaß | Bogenmaß | |
| n-Eck | ||||||
| Dreieck | ||||||
| Viereck | ||||||
| Fünfeck | ||||||
| Sechseck | ||||||
| Achteck | ||||||
| Zehneck | ||||||
| Zwölfeck | ||||||
Längen

Die wichtigsten Kenngrößen einfacher regelmäßiger Polygone können mit Hilfe des Bestimmungsdreiecks, das von dem Mittelpunkt und zwei benachbarten Ecken des Polygons gebildet wird, ermittelt werden. Das Bestimmungsdreieck ist gleichschenklig mit dem Spitzenwinkel , den Basiswinkeln , den Schenkeln , der Basis und der Höhe .[2] Wird das Bestimmungsdreieck entlang der Höhe (dem Apothema) in zwei rechtwinklige Dreiecke unterteilt, ergeben sich mit dem oben angegebenen Mittelpunktswinkel und den trigonometrischen Funktionen (Sinus und Kosinus, Tangens und Kotangens sowie Sekans und Kosekans) die folgenden Beziehungen zwischen der Seitenlänge , dem Umkreisradius und dem Inkreisradius :[3]
Für manche Werte von lassen sich explizite Formeln für die Funktionswerte der trigonometrischen Funktionen (siehe Formelsammlung Trigonometrie) und damit für die Längen in einfachen regelmäßigen Polygonen angeben, zum Beispiel:[3]
| Polygon | Seitenlänge gegeben | Umkreisradius gegeben | Inkreisradius gegeben | |||
|---|---|---|---|---|---|---|
| Umkreisradius | Inkreisradius | Seitenlänge | Inkreisradius | Seitenlänge | Umkreisradius | |
| n-Eck | ||||||
| Dreieck | ||||||
| Viereck | ||||||
| Fünfeck | ||||||
| Sechseck | ||||||
| Achteck | ||||||
| Zehneck | ||||||
| Zwölfeck | ||||||
Umfang und Flächeninhalt
Der Umfang eines einfachen regelmäßigen Polygons ist das -fache der Seitenlänge und damit
- .
Der Flächeninhalt eines einfachen regelmäßigen Polygons ist entsprechend das -Fache der Fläche des Bestimmungsdreiecks:[3]
- .
Die letzte Gleichung folgt dabei aus der Doppelwinkelformel. Damit ergeben sich beispielsweise die folgenden expliziten Formeln für den Umfang und den Flächeninhalt einfacher regelmäßiger Polygone:[3]
| Polygon | Seitenlänge gegeben | Umkreisradius gegeben | Inkreisradius gegeben | |||
|---|---|---|---|---|---|---|
| Umfang | Flächeninhalt | Umfang | Flächeninhalt | Umfang | Flächeninhalt | |
| Monotonie | steigend | steigend | steigend | steigend | fallend | fallend |
| n-Eck | ||||||
| Dreieck | ||||||
| Viereck | ||||||
| Fünfeck | ||||||
| Sechseck | ||||||
| Achteck | ||||||
| Zehneck | ||||||
| Zwölfeck | ||||||
Monotonie und Grenzwert von Flächeninhalt und Umfang
Es ist nicht immer offensichtlich, dass der Umfang und der Flächeninhalt des regelmäßigen Polygons streng monoton steigt oder streng monoton fällt, wenn größer wird. Da bei der Beschreibung von Flächeninhalt und Umfang die Sinus- und Tangensfunktion eine wichtige Rolle spielen, werden zunächst nützliche Eigenschaften dieser Funktionen bereitgestellt.
Eigenschaften der Tangens- und Sinusfunktionen
Aus der Reihendarstellung der Tangensfunktion folgt für :
- die Ungleichung und
- ist streng monoton steigend mit .
Ersetzt man durch , so folgt aus der Kettenregel für eine Umkehrung der Monotonie. Für gilt dann:
- ist streng monoton fallend und .
Für gilt:
- ist streng monoton fallend und .
Die Monotonie ergibt sich mit Hilfe der Ableitung und , der Grenzwert mit der Regel von de L’Hospital. Ersetzt man durch , ergibt sich für :
- ist streng monoton steigend und .
Bei vorgegebenem Umkreisradius
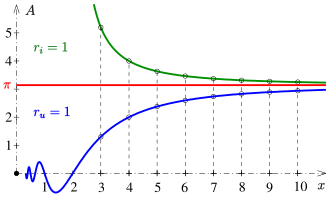
Wenn der Umkreisradius gegeben ist, kann der Flächeninhalt mit der Funktion beschrieben werden (siehe oben).
Aus den Eigenschaften der Sinusfunktion (siehe oben) folgt, dass die Funktion für alle reellen Zahlen streng monoton steigt. Für den Grenzwert erhält man mit
Dies ist der Flächeninhalt des Umkreises.
Analog ergibt sich die strenge Monotonie des Umfangs . Der Grenzwert des Umfangs ist
Dies ist der Umfang des Umkreises.
Bei vorgegebenem Inkreisradius
In diesem Fall wird der Flächeninhalt durch die Funktion beschrieben. Wie im vorigen Abschnitt zeigt man: Für alle reellen Zahlen ist streng monoton steigend und es ist . Die strenge Monotonie des Umfangs lässt sich ebenso beweisen.
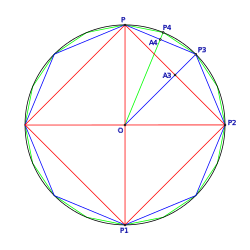
Diagonalen

Von jeder Ecke eines regelmäßigen -Ecks gehen Diagonalen bis aus. Die Länge der Diagonalen kann wiederum mit Hilfe des Bestimmungsdreiecks, das von dem Mittelpunkt des Polygons und den beiden Endpunkten der Diagonale gebildet wird, ermittelt werden. Das Bestimmungsdreieck der -ten Diagonale, , ist wieder gleichschenklig und hat die Schenkel , die Basis und den Spitzenwinkel . Damit ergibt sich für die Länge der -ten Diagonale
- .
Für die Längen der Diagonalen in einem einfachen regelmäßigen Polygon gilt die Identität
- .
Durch Drehung der Diagonalen um den Winkel mit dem Mittelpunkt als Drehzentrum oder aus dem Kreiswinkelsatz, denn jedes regelmäßige Polygon hat einen Umkreis, folgt, dass die kleinen Dreiecke der Dreieckszerlegung mit den Seitenlängen , und die Innenwinkel , und hat. Daraus ergibt sich mithilfe des Sinussatz die genannte Formel für die Länge der -ten Diagonale.[4]
Eine andere Möglichkeit ist die Verwendung des Kosinussatz und vollständige Induktion.
Wenn der Umkreis des regelmäßigen Polygons mit dem Durchmesser betrachtet wird, kann alternativ der Satz des Thales oder auch der Sekanten-Tangenten-Satz verwendet werden.
Ist die Eckenzahl des Polygons gerade, sind daher Diagonalen unterschiedlich lang. Ist die Eckenzahl ungerade, gibt es verschieden lange Diagonalen.
Bei gegebener Seitenlänge ergeben sich beispielsweise die folgenden expliziten Formeln für die Längen der Diagonalen einfacher regelmäßiger Polygone:
| Polygon | Diagonalen | ||||
|---|---|---|---|---|---|
| Diagonale | Diagonale | Diagonale | Diagonale | Diagonale | |
| Viereck | |||||
| Fünfeck | |||||
| Sechseck | |||||
| Achteck | |||||
| Zehneck | |||||
| Zwölfeck | |||||
Eigenschaften
Symmetrien

Die Symmetriegruppe eines regelmäßigen -Ecks ist die Diedergruppe . Die Diedergruppe weist die Ordnung auf und besteht aus
- Rotationen der zyklischen Gruppe und
- Spiegelungen an den Symmetrieachsen durch den Mittelpunkt des Polygons.
Ist gerade, dann verläuft die eine Hälfte der Symmetrieachsen durch zwei gegenüberliegende Ecken und die andere Hälfte durch zwei Mittelpunkte gegenüberliegender Seiten. Ist ungerade, dann verlaufen alle Symmetrieachsen durch eine Ecke und den Mittelpunkt der gegenüberliegenden Seite.
Jedes regelmäßige Polygon mit gerader Eckenzahl ist auch punktsymmetrisch bezüglich seines Mittelpunkts.
Zerlegungen

Die Gesamtzahl aller Diagonalen in einem regelmäßigen -Eck ergibt sich zu (Folge A000096 in OEIS), da von jeder der Ecken Diagonalen ausgehen und bei dieser Zählung alle Diagonalen doppelt gezählt werden. Bei einem einfachen regelmäßigen Polygon mit gerader Eckenzahl verlaufen alle Diagonalen durch den Mittelpunkt des Polygons. Bei ungerader Eckenzahl wird durch die Diagonalen im Inneren eine verkleinerte Kopie des Polygons gebildet. Die Anzahl der Schnittpunkte der Diagonalen im Inneren eines einfachen regelmäßigen -Ecks ergibt die Folge[5]
Diese Folge ganzer Zahlen ist nicht monoton steigend.
Jeweils 4 beliebige Eckpunkte des regelmäßigen -Ecks bilden ein konvexes Viereck. Die zwei Diagonalen des Vierecks schneiden sich in einem Punkt. Umgekehrt gehört jeder Schnittpunkt zu mindestens zwei Diagonalen des regelmäßigen -Ecks.
Für ungerades schneiden sich immer nur 2 Diagonalen in einem Punkt.[5] Die Anzahl der Schnittpunkte ist daher gleich der Anzahl der Möglichkeiten, 4 der Eckpunkte auszuwählen, wenn die Reihenfolge nicht berücksichtigt wird, also die Anzahl der Kombinationen ohne Wiederholung:
Für gerades größer gleich 6 schneiden sich auch mehr als 2 Diagonalen in einem Punkt. In diesem Fall ist die Anzahl der Schnittpunkte kleiner als .
Die Anzahl der Teilpolygone, die durch eine vollständige Zerlegung eines einfachen regelmäßigen -Ecks entlang der Diagonalen entsteht, ergibt die Folge
Für ungerades ist diese Anzahl gleich
und kleiner für gerades . Auch diese Folge ganzer Zahlen ist nicht monoton steigend.[5]
Die Anzahl der Möglichkeiten, ein einfaches regelmäßiges -Eck überschneidungsfrei entlang der Diagonalen in Teilpolygone zu zerteilen, wird durch die kleinen Schröder-Zahlen angegeben. Sollen diese Teilpolygone ausschließlich Dreiecke sein, wird die Anzahl der Möglichkeiten durch die Catalan-Zahlen angegeben. Allgemeiner werden auch Zerlegungen regelmäßiger Polygone untersucht, bei denen nicht nur die Diagonalen verwendet werden dürfen, zum Beispiel die Zerlegung in flächengleiche Dreiecke.
Zusammenhang mit Sternpolygonen
Es können auch nur gleich lange Diagonalen, aber nicht die Seiten in einem regelmäßigen -Eck eingezeichnet werden.
Werden die Ecken mit Indexen durchnummeriert und nur die mit einer geraden Strecke verbunden, deren – fortlaufende – Indexe die Differenz haben, dann sind diese Strecken gleich lange Diagonalen und es entsteht ein regelmäßiges Sternpolygon. Umgangssprachlich kann man auch sagen, dass immer jeder -te Punkt einer gleichmäßig mit Punkten unterteilten Kreislinie mit einer geraden Strecke verbunden wird. Die formale Bezeichnung für ein solches Sternpolygon ist -Stern (siehe Schläfli-Symbol).
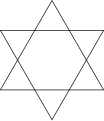
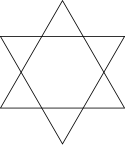
Wird immer jede zweite Ecke innerhalb eines regelmäßigen Fünfecks verbunden, dann entsteht ein regelmäßiger -Stern, nämlich das Pentagramm. Wird immer jede zweite Ecke innerhalb eines regelmäßigen Sechsecks verbunden, dann entsteht ein regelmäßiger -Stern, nämlich das Hexagramm, das auch als Davidstern bekannt ist.
Für und gibt es folgende regelmäßige Sternpolygone:
- {5/2}-Stern (Pentagramm)
- {6/2}-Stern (Hexagramm oder Davidstern)
- {7/2}-Stern
- {7/3}-Stern
- {8/2}-Stern (Achtort)
- {8/3}-Stern (Achterstern)
Abstände

Nach dem Satz von Viviani ist die Summe der senkrechten Abstände von einem beliebigen Punkt im Inneren eines einfachen regelmäßigen Polygons zu den Polygonseiten gleich der Summe der Abstände vom Mittelpunkt zu den Seiten und damit gleich . Betrachtet man nämlich die Dreiecke, die von dem Punkt und jeweils zwei benachbarten Eckpunkten gebildet werden, dann ist die Summe der Flächeninhalte dieser Dreiecke gleich dem gesamten Flächeninhalt des Polygons, also
- .
Die Aussage ergibt sich dann durch Dividieren beider Seiten der Gleichung durch . Weitere Identitäten in regelmäßigen Polygonen sind:[6]
- Die Summe der Abstände von den Eckpunkten zu einer beliebigen Umkreistangente ist .
- Die Summe der Abstandsquadrate von den Eckpunkten zu einem beliebigen Punkt auf dem Umkreis ist .
- Die Summe der Abstandsquadrate von den Seitenmitten zu einem beliebigen Punkt auf dem Umkreis ist .
Das Produkt der Abstände von einem Eckpunkt zu allen anderen Eckpunkten ergibt sich in einem regelmäßigen Polygon zu
- .
Maximalität

Regelmäßige Polygone maximieren nach dem Satz von Zenodoros den Flächeninhalt im Vergleich zu anderen Polygonen in folgender Weise:
- Von allen -Ecken mit gleichem Umfang hat das regelmäßige -Eck den größten Flächeninhalt.
- Von allen in einen gegebenen Kreis einbeschriebenen -Ecken hat das regelmäßige -Eck den größten Flächeninhalt.
- In jeder endlichen Menge regelmäßiger Polygone mit gleichem Umfang hat dasjenige mit den meisten Ecken den größten Flächeninhalt.
Andererseits gilt aber auch die isoperimetrische Ungleichung:
- Ein Kreis hat einen größeren Flächeninhalt als jedes regelmäßige Polygon mit gleichem Umfang.
Darstellung mit Koordinaten

Kartesische Koordinaten:
Die Ecken eines regelmäßigen -Ecks mit den Eckpunkten auf dem Kreis um den Ursprung mit Radius (Umkreisradius) und haben für die Koordinaten
Polarkoordinaten:
Die Polarkoordinaten des Punktes sind
- .
Definition als Menge von Punkten
Definition als Schnittmenge von Halbebenen
Ein regelmäßiges -Eck kann mithilfe der Geraden, die jeweils durch zwei benachbarte Eckpunkte verlaufen, definiert werden. Das regelmäßige Polygon ist die Schnittmenge der Halbebenen, die auf der Seite des Koordinatenursprungs liegen. Sie kann formal geschrieben werden als
Jede dieser Halbebenen ist die Menge aller Punkte, die die zur Zwei-Punkte-Gleichung der Geraden gehörende Ungleichung erfüllen.
Für das Innere des regelmäßige Polygons muss in den Ungleichungen jeweils durch ersetzt werden und für den Rand muss in 1 oder 2 Ungleichungen durch ersetzt werden, sodass ein System aus Gleichungen und Ungleichungen entsteht. Bei 1 Gleichung definiert die Menge eine Seite und bei 2 Gleichungen mit aufeinander folgenden Indexen und eine Ecke.
Definition als Voronoi-Zelle
Ein regelmäßigen -Eck kann als zweidimensionale Voronoi-Zelle, also als Region eines zweidimensionalen Voronoi-Diagramms definiert werden. Eine Voronoi-Zelle ist eine Menge von Punkten in der Ebene. Das Zentrum des regelmäßigen Polygons ist der Koordinatenursprung . Die anderen Zentren des Voronoi-Diagramms bilden die Ecken eines anderen regelmäßigen -Ecks mit dem doppelten Inkreisradius . Nach der Definition einer Voronoi-Zelle kann diese Menge von Punkten formal geschrieben werden als
Dabei bezeichnet den euklidischen Abstand in der Ebene.[7]
Konstruktion
Zirkel und Lineal

Die Frage, welche regelmäßigen -Ecke unter ausschließlicher Verwendung von Zirkel und Lineal konstruiert werden können, wurde bereits in der Antike untersucht, aber erst im 19. Jahrhundert von Carl Friedrich Gauß und Pierre Wantzel abschließend beantwortet. Demnach ist ein regelmäßiges Polygon genau dann mit Zirkel und Lineal konstruierbar, wenn die Zahl seiner Seiten von der Form
ist, wobei und paarweise voneinander verschiedene fermatsche Primzahlen sind. Das kleinste nicht konstruierbare regelmäßige Polygon ist damit das regelmäßige Siebeneck. Lässt man zur Konstruktion zusätzlich ein Hilfsmittel zur Dreiteilung eines Winkels zu, so sind alle regelmäßigen Polygone mit Seitenzahlen der Form
konstruierbar, wobei und verschiedene Pierpont-Primzahlen größer als drei sind. Auf diese Weise sind beispielsweise auch das regelmäßige Siebeneck,[9] das regelmäßige Neuneck und das regelmäßige Dreizehneck[10] konstruierbar, nicht jedoch das regelmäßige Elfeck. Konkrete Konstruktionsvorschriften für regelmäßige Polygone zu finden gestaltet sich jedoch mit wachsender Eckenzahl schnell als sehr aufwändig. Es gibt aber solche Konstruktionsvorschriften unter anderem für das 17-Eck, das 257-Eck und das 65537-Eck.
Apeirogon als Grenzform
Wird bei wachsender Seitenzahl stattdessen die Seitenlänge konstant gehalten, nähert sich die Form eines einfachen regelmäßigen -Ecks einer degenerierten geometrischen Figur an, die Apeirogon (von griechisch ἄπειρον, das Unbeschränkte) genannt wird und mit dem Schläfli-Symbol bezeichnet wird.[11] Ein Apeirogon kann als eine Aneinanderreihung unendlich vieler gleich langer Linienstücke der Form
visualisiert werden oder auch als Kreis mit einem unendlich großen Radius angesehen werden. Die Innenwinkel eines Apeirogons sind gestreckte Winkel und messen daher
- .
Im hyperbolischen Raum ist ein Apeirogon jedoch nicht mehr degeneriert und besitzt eine Reihe interessanter Eigenschaften. So lässt sich beispielsweise die hyperbolische Ebene durch Apeirogone auf verschiedene Weisen regelmäßig parkettieren.
Schachtelungen

Wird in einen Einheitskreis ein regelmäßiges Dreieck einbeschrieben, in dessen Inkreis dann ein regelmäßiges Viereck, in wiederum dessen Inkreis ein regelmäßiges Fünfeck und so weiter, dann konvergiert die Folge der Inkreisradien gegen den Grenzwert
der Kepler-Bouwkamp-Konstante oder polygon inscribing constant genannt wird. Analog konvergiert die Folge der Umkreisradien, wenn um einen Einheitskreis abwechselnd regelmäßige Polygone mit wachsender Seitenzahl und deren Umkreise umbeschrieben werden, gegen den Grenzwert
der als polygon circumscribing constant bekannt ist.
Das Produkt der beiden Konstanten ist 1.
Verwendung
Polygonalzahlen
In der Zahlentheorie werden die Polygonalzahlen und die zentrierten Polygonalzahlen betrachtet, die dadurch entstehen, dass mit einer bestimmten Zahl von Steinen regelmäßige Polygone gelegt werden. Nach dem fermatschen Polygonalzahlensatz lässt sich jede Primzahl als Summe von höchstens solcher -Eckszahlen darstellen. Ein bekannter Spezialfall dieses Satzes ist der Vier-Quadrate-Satz von Joseph Louis Lagrange. Die dreidimensionalen Verallgemeinerungen der Polygonalzahlen heißen Pyramidalzahlen.
Näherung von π

Archimedes setzte im 3. Jahrhundert v. Chr. erstmals regelmäßige Polygone ein, um die Kreiszahl mit Hilfe der Exhaustionsmethode näherungsweise zu berechnen. Hierzu verwendete er eine Folge von Polygonen, die einem Einheitskreis mit Radius ein- beziehungsweise umbeschrieben sind. Er begann dabei mit dem regelmäßigen Sechseck und führte die Reihe mit dem Zwölfeck, dem Vierundzwanzigeck, dem 48-Eck bis hin zum 96-Eck fort. Auf diese Weise gewann er die Abschätzung
- .
Im Mittelalter setzten chinesische und persische Wissenschaftler diese Berechnungen mit dem 192-Eck und weiteren Polygonen fort. Ludolph van Ceulen führte im 16. Jahrhundert Berechnungen bis zum regelmäßigen -Eck durch und ermittelte so die Kreiszahl bis auf 35 Stellen genau. Allgemein ergeben sich durch die Approximation eines Kreises mit ein- und umschriebenen regelmäßigen -Ecken Abschätzungen von der Form
- .
Die trigonometrischen Terme lassen sich dabei mit Hilfe von Rekursionsformeln berechnen.
Parkettierungen
Regelmäßige Polygone können auch als Kacheln einer Parkettierung der Ebene verwendet werden. Wird nur ein regelmäßiges Polygon als Kachel zugelassen, wobei die Kacheln Kante an Kante angeordnet werden müssen, ergeben sich die drei platonischen Parkettierungen aus regelmäßigen Dreiecken, Vierecken und Sechsecken. Werden verschiedene regelmäßige Polygone als Kacheln zugelassen, wobei an den Ecken stets die gleiche Anordnung von Polygonen zusammenstoßen muss, erhält man die acht archimedischen Parkettierungen. Eine weitaus größere Vielfalt an Parkettierungen ergibt sich, wenn an den Ecken unterschiedliche Kombinationen von Polygonen zugelassen werden. Die Parkettierung mit regelmäßigen Sechsecken hat die geringste Umfangslänge pro Flächeneinheit, siehe Bienenwaben-Satz.
- Sechseckgitter
- 3-3-4-3-4
- 3-3-3-3-6 (zwei gespiegelte Varianten)
- 3-4-6-4
- 4-6-12
- (c) Baelde, CC BY-SA 3.03-4-4-6 und 3-6-3-6
Polyeder
Im dreidimensionalen Raum bilden regelmäßige Polygone die Seitenflächen von regulären Polyedern. Zu den konvexen Polyedern, die nur regelmäßige Polygone als Seitenflächen haben, gehören
- die 5 platonischen Körper
- die 13 archimedischen Körper
- die regulären Prismen
- die uniformen Antiprismen
- die 92 Johnson-Körper
- bestimmte regelmäßige Pyramiden
- bestimmte regelmäßige Doppelpyramiden
Einige Polyeder gehören zu mehreren dieser Kategorien.
Wird nur ein regelmäßiges Polygon verwendet, wobei an den Ecken immer gleich viele Polygone zusammenstoßen müssen, erhält man die fünf platonischen Körper Tetraeder, Hexaeder, Oktaeder, Dodekaeder und Ikosaeder. Werden verschiedene regelmäßige Polygone als Seitenflächen zugelassen, wobei an den Ecken stets die gleiche Anordnung von Polygonen zusammenstoßen muss, ergeben sich die 13 archimedischen Körper sowie die regulären Prismen und die uniformen Antiprismen. Werden auch nichtuniforme Ecken zugelassen, erhält man die 92 Johnson-Körper. Mit manchen dieser Polyeder lässt sich auch der dreidimensionale Raum parkettieren.
Es gibt auch Sternkörper, deren Seitenflächen regelmäßige Polygone sind, wie zum Beispiel das Sterntetraeder.
- Quadratische Pyramide
- Dreiecksbipyramide (Johnson-Körper J12)
- Reguläres dreieckiges Prisma
- Uniformes hexagonales Antiprisma
- (c) DTR, CC BY-SA 3.0
- Ikosaederstumpf (Fußballkörper)
- Dreieckskuppel
Vorkommen
Architektur

Regelmäßige Polygone werden in der Architektur häufig als Grundriss von Zentralbauten verwendet. Beispielsweise sind
- quadratisch: die ägyptischen Pyramiden, Vierungstürme im Kirchenbau
- fünfeckig: das Pentagon in Washington, die Festung Rosenberg in Kronach (siehe auch Fünfeckturm, Fünfecke in Architektur und Festungsbau)
- sechseckig: die Festung Saarlouis, das Fort Jefferson in Florida, die Telefonkioske in Dänemark (siehe auch Vorkommen von Sechsecken und hexagonalen Strukturen, Liste sechseckiger Kirchen)
- siebeneckig: das Kultur- und Kongresszentrum Liederhalle in Stuttgart, das Fürstliche Mausoleum in Stadthagen
- achteckig: der Felsendom in Jerusalem, das Castel del Monte in Apulien (siehe auch Oktogon (Architektur))
- neuneckig: die Festungsstadt Palmanova, die Häuser der Andacht der Bahai
- zwölfeckig: der Torre del Oro in Sevilla, die Kirche La Vera Cruz in Segovia (siehe auch Zwölfeck in der Architektur)
- vierzehneckig: die Kirche Notre-Dame de l’Assomption in Rieux-Minervois
- sechzehneckig: der Zentralbau des Aachener Doms, die Stierkampfarena La Malagueta in Málaga
Numismatik

Neben kreisrunden Münzen gibt es auch Münzen mit polygonaler Form. Solche in der Numismatik als Klippen bezeichnete Münzen wurden früher als Notmünzen geprägt, sie finden sich gelegentlich aber auch als Kurs- oder Gedenkmünzen. Beispiele für im Umlauf befindliche Klippen in Form eines regelmäßigen Polygons sind:
- quadratisch: die 50-Cent-Münze der niederländischen Antillen
- sechseckig: die indische 20-Paise-Münze
- siebeneckig: die britischen 20- und 50-Pence-Münzen
- achteckig: die chilenischen Ein- und Fünf-Peso-Münzen
- elfeckig: die indische Zwei-Rupien-Münze
- zwölfeckig: die australische 50-Cent-Münze
Moderne Klippen haben dabei häufig die Form eines Reuleaux-Polygons mit nach außen gekrümmten Seiten, damit sie einfacher von Münzautomaten detektierbar sind.
Natur

Regelmäßige polygonale Strukturen kommen auch in der Natur vor. Manche Atome können cyclische Verbindungen eingehen, wie zum Beispiel der Benzolring C6H6 in Form eines regelmäßigen Sechsecks. Auch in der Struktur von Kristallen treten regelmäßige Polygone auf, beispielsweise in kubischen oder hexagonalen Kristallsystemen. In der Biologie finden sich regelmäßige Polygone unter anderem bei Okrafrüchten (fünfeckig) und Bienenwaben (sechseckig).
Symbolik
Einige regelmäßige Polygone haben neben der geometrischen auch eine symbolische Bedeutung, zum Beispiel das Dreiecksymbol oder das Pentagramm. Verkehrszeichen, insbesondere Vorfahrtsschilder, haben häufig die Form eines regelmäßigen Polygons mit abgerundeten Ecken.
Siehe auch
- Stern (Geometrie)
- Platonische Parkettierung
- Platonischer Körper
- Archimedischer Körper
- Prisma (Geometrie)
- Antiprisma
- Johnson-Körper
- Regelmäßige Pyramide
- Regelmäßige Doppelpyramide
Literatur
- Harold Scott MacDonald Coxeter: Regular Polytopes. Courier Dover Publications, 1973, ISBN 0-486-61480-8.
- John M. Lee: Axiomatic Geometry. American Mathematical Society, 2013, ISBN 978-0-8218-8478-2.
- Roger A. Johnson: Advanced Euclidean Geometry. Dover Publications, 2007, ISBN 978-0-486-46237-0.
Weblinks
- Regular Polygons. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org).
- Eric W. Weisstein: Regular Polygon. In: MathWorld (englisch).
- Wkbj79: Regular Polygon. In: PlanetMath. (englisch)
- Jürgen Köller: Regelmäßiges Vieleck. In: Mathematische Basteleien. 2005, abgerufen am 7. November 2014.
- Edmund Weitz: Das regelmäßige 17-Eck. In: YouTube. 2017, abgerufen am 27. August 2020.
- CalculatorSoup: Regular Polygon Calculator (Web Application zum Berechnen)
- Rechneronline: Regelmäßiges Vieleck - Rechner (Web Application zum Berechnen)
- Wolfram Demonstrations Project: Regular Polygon Maker (Web Application zum Zeichnen)
- GeoGebra: Creating Regular Polygons Practice (Web Application zum Zeichnen)
Einzelnachweise
- ↑ a b c Harold Scott MacDonald Coxeter: Regular Polytopes. Courier Dover Publications, 1973, S. 2.
- ↑ Siegfried Völkel, Horst Bach, Heinz Nickel, Jürgen Schäfer: Mathematik für Techniker. Carl Hanser Verlag, 2014, S. 169.
- ↑ a b c d Hans-Jochen Bartsch: Taschenbuch mathematischer Formeln für Ingenieure und Naturwissenschaftler. Carl Hanser Verlag, 2014, S. 141–143.
- ↑ Anne Fontaine, Susan Hurley, Forum Geometricorum: Proof by Picture: Products and Reciprocals of Diagonal Length Ratios in the Regular Polygon
- ↑ a b c Bjorn Poonen, Michael Rubinstein: The number of intersection points made by the diagonals of a regular polygon. In: SIAM J. Discrete Mathematics. Band 11, Nr. 1, 1998, S. 135–156, doi:10.1137/S0895480195281246. Korrigierte Version: arxiv:math/9508209
- ↑ Roger A. Johnson: Advanced Euclidean Geometry. Dover Publications, 2007, S. 72.
- ↑ Miloš Dimčić, Fakultät Architektur und Stadtplanung der Universität Stuttgart: Structural Optimization of Grid Shells Based on Genetic Algorithms
- ↑ Herbert W. Richmond: A Construction for a regular polygon of seventeen sides. In: The Quarterly Journal of Pure and Applied Mathematics. Band 26, 1893, S. 206–207 (Beschreibung und Abbildung Fig. 6).
- ↑ Andrew Gleason: Angle Trisection, the Heptagon, and the Triskaidecagon. In: The American Mathematical Monthly. Band 95, Nr. 3, 1988, S. 185–194, hier S. 186 ff. (FIG.1. Construction of a regular heptagon [PDF; abgerufen am 15. Mai 2019]).
- ↑ Andrew Gleason: Angle Trisection, the Heptagon, and the Triskaidecagon. In: The American Mathematical Monthly. Band 95, Nr. 3, 1988, S. 185–194, hier S. 193 ff. (FIG. 4. Construction of a regular triskaidecagon [PDF; abgerufen am 15. Mai 2019]).
- ↑ Harold Scott MacDonald Coxeter: Regular Polytopes. Courier Dover Publications, 1973, S. 45.
Auf dieser Seite verwendete Medien
Autor/Urheber: Tomruen, Lizenz: CC BY-SA 3.0
Recolor File:H2_tiling_iii-3.png for *∞∞∞∞ symmetry
Autor/Urheber: original by Tomruen
vectorization by B. Jankuloski, Lizenz: CC0
A regular apeirogon.
Autor/Urheber:
- Triangular_prism.png: mathematics
- derivative work: Lovasoa (talk)
vue tridimensionnelle d'un prisme triangulaire
Regular tiling of hyperbolic plane, ∞x∞x∞x. Generated by Python code at User:Tamfang/programs.
Dual:





Autor/Urheber: Quartl, Lizenz: CC BY-SA 3.0
Alternierende Folgen einbeschriebener (links) und umschriebener (rechts) Kreise und regelmäßiger Polygone mit wachsender Seitenzahl
Autor/Urheber: Quartl, Lizenz: CC BY-SA 3.0
Bestimmungsdreieck beim regelmäßigen Sechseck
Autor/Urheber: World Coin Gallery, Lizenz: CC BY-SA 3.0
Egypt 1933, 2.5 Milliemes, copper-nickel, octagonal
Autor/Urheber: R. A. Nonenmacher, Lizenz: CC BY-SA 4.0
Semiregular Tiling 3-3-3-3-6 (Snub Hexagonal)
Autor/Urheber: R. A. Nonenmacher, Lizenz: CC BY-SA 4.0
Semiregular Tiling 3-4-6-4 (Small Rhombitrihexagonal)
|
Dieses Bild zeigt ein Objekt, das im National Register of Historic Places der Vereinigten Staaten verzeichnet ist. Die Referenznummer lautet 89000932. |
Autor/Urheber: Quartl, Lizenz: CC BY-SA 3.0
Symmetrieachsen eines regelmäßigens Fünfecks und eines regelmäßigens Sechsecks
Autor/Urheber: R. A. Nonenmacher, Lizenz: CC BY-SA 4.0
Semiregular Tiling 3-3-4-3-4 (Snub Square)
(c) Baelde, CC BY-SA 3.0
The image evokes a covering of the entire Euclidean plane with an infinite number of convex regular polygons: equilateral triangles, squares, hexagons. All polygons with the same number of sides are congruent. Every edge of any polygon is shared by two polygons placed edge to edge.
Autor/Urheber:
Beschreibung: Die Kärntner Biene (Apis mellifera carnica, auch: Krainer Biene) ist eine natürlich entstandene Rasse der Westlichen Honigbiene (Apis mellifera). Von den Imkern wird sie auch einfach Carnica genannt.
Autor/Urheber:
Lars H. Rohwedder (Benutzer:RokerHRO)
, Lizenz: PD-SchöpfungshöheSiebenstern (Heptragramm) Variante 2
Simple picture of a Stella octangula / Star Tetrahedron
Autor/Urheber: Stefan Friedrich Birkner, Lizenz: CC BY-SA 3.0
37 Kugeln in Form eines Sechsecks angeordnet.
Autor/Urheber:
Lars H. Rohwedder (Benutzer:RokerHRO)
, Lizenz: PD-SchöpfungshöheOctagramm (Achtstern) - Variante 2
Polígono regular inscrito en una circunferencia para el calculo de Pi.
Autor/Urheber: Quartl, Lizenz: CC BY-SA 3.0
Ein regelmäßiges Sechseck mit Bezeichnungen
Autor/Urheber: Quartl, Lizenz: CC BY-SA 3.0
Satz von Viviani für ein regelmäßiges Achteck: die Summe der Abstände von einem beliebigen Punkt im Inneren des Achtecks zu den Seiten ist gleich der Summe der Abstände vom Mittelpunkt zu den Seiten.
Autor/Urheber: R. A. Nonenmacher, Lizenz: CC BY-SA 4.0
Semiregular Tiling 4-6-12 (Great Rhombitrihexagonal)
Autor/Urheber: Stefan Friedrich Birkner, Lizenz: CC BY-SA 3.0
31 Kugeln in Form eines Fünfecks angeordnet.
Autor/Urheber: Quartl, Lizenz: CC BY-SA 3.0
Zerlegungen eines regelmäßigens Siebenecks und eines regelmäßigens Achtecks mit Hilfe aller Diagonalen
Autor/Urheber: Quartl, Lizenz: CC BY-SA 3.0
In einem Kreis einbeschriebenes unregelmäßiges und regelmäßiges Sechseck.
Autor/Urheber: H. W. Richmond, derivative work: Petrus3743, Lizenz: CC BY-SA 4.0
Siebzehneck, Konstruktion nach H. W. Richmond
W3C-validity not checked.
Autor/Urheber: R. A. Nonenmacher, Lizenz: CC BY-SA 4.0
Regular Tiling 6-3 (Hexagonal)
Autor/Urheber: Perey, Lizenz: CC BY 3.0
Regular polygons, star polygons, and star figures, with up to 16 edges.
Autor/Urheber: Quartl, Lizenz: CC BY-SA 3.0
Diagonalen in einem regelmäßigen Achteck mit Bestimmungsdreieck
Autor/Urheber:
Lars H. Rohwedder (Benutzer:RokerHRO)
, Lizenz: PD-SchöpfungshöheHeptagramm (Siebenstern) Variante 1
Autor/Urheber:
Lars H. Rohwedder (Benutzer:RokerHRO)
, Lizenz: PD-SchöpfungshöheOctagramm (Achtstern) - Variante 1