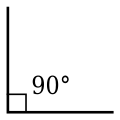
Rechter Winkel

Ein rechter Winkel, kurz auch Rechter, ist ein Winkel von 90° und damit der vierte Teil eines Vollwinkels zu 360°. Zwei Geraden oder Strecken, die sich in einem rechten Winkel schneiden oder berühren, werden als rechtwinklig, senkrecht oder orthogonal bezeichnet. Rechte Winkel treten in vielen geometrischen Figuren und Konstruktionen auf und werden in Zeichnungen durch einen kleinen Viertelkreis mit Punkt oder durch ein kleines Quadrat gekennzeichnet. Der rechte Winkel war neben dem Vollwinkel zeitweise eine gesetzliche Einheit in Deutschland und in der Schweiz.
Definition
Sowohl Euklid in seinem Werk Die Elemente (ca. 300 v. Chr.), als auch David Hilbert in seinem Axiomensystem der euklidischen Geometrie (1899) definieren einen rechten Winkel als einen Winkel, der kongruent zu seinem Nebenwinkel ist:
„Wenn eine gerade Linie, auf eine gerade Linie gestellt, einander gleiche Nebenwinkel bildet, dann ist jeder der gleichen Nebenwinkel ein Rechter“
Das Adjektiv „recht“ meint hierbei nicht rechts, sondern recht im Sinne von aufrecht (lateinisch rectus).[2] Alternativ dazu wird spätestens seit dem 16. Jahrhundert ein rechter Winkel auch als ein Winkel, zu dem ein Viertelkreis gehört, definiert.[2] Beide Definitionen sind zueinander äquivalent, denn zwei Nebenwinkel ergeben zusammen einen gestreckten Winkel, dem ein Halbkreis entspricht.
Beispiele
In der Ebene bilden beispielsweise einen rechten Winkel:
- die Koordinatenachsen eines kartesischen Koordinatensystems
- zwei benachbarte Seiten eines Rechtecks
- die beiden Katheten eines rechtwinkligen Dreiecks
- die beiden Diagonalen eines Drachenvierecks
- die beiden Halbachsen einer Ellipse
- die Verbindungslinien eines Punkts auf einem Halbkreis mit den Endpunkten des Durchmessers (Satz des Thales)
Im Raum bilden beispielsweise einen rechten Winkel:
- je zwei der Koordinatenachsen eines dreidimensionalen kartesischen Koordinatensystems
- zwei benachbarte Kanten eines Quaders
- je zwei der drei Raumdiagonalen eines Oktaeders
- zwei zueinander orthogonale Vektoren
- das Lot auf eine Ebene mit jeder Gerade der Ebene durch den Lotfußpunkt
In einem orthogonalen Polygon oder einem orthogonalen Polyeder bilden alle benachbarten Kanten rechte Winkel.
Bestimmung rechter Winkel

Zwischen Strecken
Zwei Strecken und bilden nach dem Satz des Pythagoras genau dann einen rechten Winkel, wenn für die Längen der Strecken
gilt. Die ganzzahligen Lösungen dieser Gleichung heißen pythagoreische Tripel. So bilden zwei Strecken, die sich in einem Punkt treffen und deren Längen bzw. Einheiten betragen, genau dann miteinander einen rechten Winkel, wenn die Verbindungsstrecke der beiden Endpunkte Einheiten lang ist, denn
- . Die Harpedonapten (Seilspanner) im alten Ägypten verwendeten dies zur Konstruktion des rechten Winkels.[3]
Zwischen Funktionsgraphen
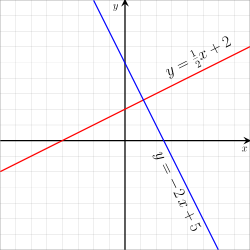
Die Graphen zweier linearer Funktionen und schneiden sich genau dann in einem rechten Winkel, wenn für das Produkt der Steigungen
gilt. Beispielsweise schneiden sich die Graphen der beiden linearen Funktionen und rechtwinklig, denn
- .
Allgemeiner schneiden sich die Graphen zweier differenzierbarer Funktionen und genau dann in einem rechten Winkel, wenn am Schnittpunkt das Produkt der Ableitungen (der Tangentensteigungen)
ergibt. So schneiden sich beispielsweise die Graphen der Funktionen und an der Stelle rechtwinklig, denn und
- .
Zwischen Kurven
Zwei sich schneidende Geraden bilden in einem kartesischen Koordinatensystem genau dann einen rechten Winkel, wenn für das Skalarprodukt der Richtungsvektoren und der beiden Geraden
gilt. So stehen beispielsweise zwei Geraden mit den Richtungsvektoren und aufeinander senkrecht, da
ist. Allgemeiner bilden zwei sich schneidende differenzierbare Kurven miteinander einen rechten Winkel, wenn das Skalarprodukt ihrer Tangentialvektoren am Schnittpunkt verschwindet.
Trigonometrie

Für die trigonometrischen Funktionen Sinus und Kosinus, Tangens und Kotangens sowie Sekans und Kosekans eines rechten Winkels gilt:
- und sind nicht definiert
Einheiten
Ein rechter Winkel entspricht in den verschiedenen Winkelmaßen:
- 1 Rechter = 90° = 90 Grad
- 1 Rechter = /2 rad im Bogenmaß (SI-Einheit)
- 1 Rechter = 100g = 100 gon = 100 Neugrad
- 1 Rechter = 8" = 8 nautische Strich
- 1 Rechter = 1600¯ = 1600 mil = 1600 artilleristische Strich
- 1 Rechter = 6h = 360m = 21600s im Stundenmaß
Vom 5. Juli 1970 bis zum 29. November 1973 war neben dem Vollwinkel (360 Grad) auch der rechte Winkel mit dem Einheitenzeichen ∟ in Deutschland eine gesetzliche Einheit.[4] Bis zum 31. Dezember 1996 war der rechte Winkel in der Schweiz gesetzliche Einheit.
Konstruktion zeichnerisch
Hilfsmittel zum Zeichnen von rechtwinkligen Linien sind beispielsweise in der Schule ein mathematisches Papier oder ein Geodreieck. Zur Konstruktion mit Zirkel und Lineal siehe Lot (Mathematik). Beim technischen Zeichnen am Reißbrett wird ein Zeichenkopf mit Zeichenschienen eingesetzt. Im metall- und holzverarbeitenden Handwerk wird zur Abmessung rechter Winkel ein Winkelmaß oder eine Lehre verwendet.
- Konstruktion eines rechten Winkels in einem Punkt , einer Gerade .
- Konstruktion eines rechten Winkels in einem Punkt , einer Halbgeraden , mithilfe des Thaleskreises
(Punkt frei wählbar). Vorteilhaft, wenn Punkt auf oder nahe am Anfangspunkt liegt.[5]
In der Praxis erhält man so natürlich immer nur Näherungen an das geometrische Konzept des rechten Winkels.
- Zeichnen rechter Winkel mit dem Geodreieck
- Zwei Haarwinkel
- Ingenieur am Reißbrett
- Ein Anschlagwinkel
Konstruktion praktisch

Zur Konstruktion rechter Winkel über längere Distanzen hinweg wurden im Laufe der Zeit verschiedene mechanische Hilfsmittel entwickelt. Die einfachste Art, einen rechten Winkel zu konstruieren, erfolgt mit einer Schnur, an der 12 gleiche Abstände markiert sind (12-Knoten-Schnur). Diese spannt man zu einem Dreieck mit den Kantenlängen . Zwischen den zwei kurzen Seiten (Katheten) liegt der rechte Winkel (genau 90°). Diese Methode wurde schon im alten Ägypten und im Mittelalter in der Baukunst benutzt. Wenn man beispielsweise mit einer Schlauchwaage eine waagrechte Linie konstruieren kann, kann man so eine senkrechte Linie konstruieren. Oder wenn man mit dem Senkblei eine senkrechte Linie konstruieren kann, kann man so eine waagrechte Linie konstruieren. Das zugrundeliegende Prinzip heißt pythagoreisches Tripel.
In der römischen Bautechnik wurde bei der Limitation von Siedlungen eine Groma zur Absteckung rechter Winkel verwendet, in neuerer Zeit kam hierfür eine Kreuzscheibe zum Einsatz. In der Geodäsie kommt bei Katastervermessungen mit dem Orthogonalverfahren ein Winkelprisma oder ein Theodolit zum Einsatz.
Heute sind diese Geräte weitgehend durch elektro-optische Entfernungsmesser, wie beispielsweise Tachymeter, abgelöst worden.
Kennzeichnung und Kodierung
Zur Kennzeichnung rechter Winkel in Zeichnungen wird im deutschsprachigen Raum sowie einer Reihe weiterer europäischer Länder ein beide Schenkel des Winkels verbindender Viertelkreis mit einem Punkt darin verwendet. Gelegentlich wird der Punkt auch weggelassen. Im englischsprachigen Raum wird zur Kennzeichnung ein beide Schenkel des Winkels verbindender und mit ihnen ein kleines Quadrat (bzw. bei schräger Darstellung Parallelogramm) bildender zweiter rechter Winkel eingezeichnet.
Im Zeichensatz werden rechte Winkel folgendermaßen definiert und kodiert:
| Zeichen | Unicode | Name | HTML | |||
|---|---|---|---|---|---|---|
| Position | Bezeichnung | hexadezimal | dezimal | benannt | ||
| ∟ | U+221F | right angle | Rechter Winkel | ∟ | ∟ | – |
| ⦜ | U+299C | right angle variant with square | Variante eines rechten Winkels mit Quadrat | ⦜ | – | – |
| ⦝ | U+299D | measured right angle with dot | Gemessener rechter Winkel mit Punkt | ⦝ | – | – |
| ⊾ | U+22BE | right angle with arc | Rechter Winkel mit Bogen | ⊾ | ⊾ | – |
Das Zeichen ∟ für den rechten Winkel wurde erstmals von dem griechischen Mathematiker Pappos im 4. Jh. n. Chr. verwendet.[6]
Historisches


Rechte Winkel sind – wie der Kreis, die Gerade etc. – Abstraktionen des menschlichen Geistes in seiner permanenten Auseinandersetzung mit der ihn umgebenden Natur und seinen eigenen Bedürfnissen.[7] Sie kommen in der belebten Natur nicht vor und sind auch in der unbelebten sichtbaren Natur äußerst selten. Wahrscheinlich realisierte der Mensch den rechten Winkel erstmals in kleinen geometrischen Zeichnungen der Höhlenmalerei sowie beim Bau von Hütten. Bei letzteren entwickelten sie sich zwischen waagerechtem Boden und aufrecht stehenden Stangen sowie zwischen senkrecht stehenden Pfosten und horizontaler Geflechtfüllung. Später erscheinen sie auch in der Flecht- und Webkunst (z. B. bei Matten und Stoffen).
Dieses einmal gefundene Grundmuster schützte vor Wind und war blickdicht; es wurde immer weiter verfeinert und so entstanden Jahrtausende später die ersten Lehm- und Steinbauten mit rechtwinkligen Zugängen sowie Ecken und Ornamenten. Waren die etwa 10- bis 12.000 Jahre alten Bauten von Göbekli Tepe noch rund, so zeigen die Kanten der dortigen großen Pfeiler eindeutig rechte Winkel; die unmittelbar aneinander gebauten Häuser von Catalhöyük in Anatolien (um 7000 v. Chr.) haben hingegen bereits allesamt ein rechtwinkliges Grundmuster. Bei den Megalithbauten der Jungsteinzeit (um 3500 v. Chr.) sind exakt rechtwinklige Konstruktionen eher selten, doch spielen sie in z. B. Stonehenge und bei einigen Dolmen durchaus eine bedeutende Rolle. Einen großen Aufschwung nahm der rechte Winkel im Bereich der Architektur durch die Herstellung von Lehmziegeln und später von Ziegelsteinen.
Während Ägypter, Griechen, Römer und selbst die mesoamerikanischen Kulturen den Rechten Winkel in der Baukunst häufig verwenden, tritt er in der Keramik sowie in einzelnen Phasen der indisch-asiatischen sowie der europäischen Baukunst (Gotik, Barock) oder bei einzelnen Architekten der Postmoderne (z. B. Antoni Gaudí, Frank Gehry oder Friedensreich Hundertwasser) in den Hintergrund.
In der Möbelkunst (Bänke, Stühle, Tische etc.) sowie in der Ornamentik kommen rechte Winkel seit der Antike in vielfältiger Weise zum Einsatz (z. B. Fischgrätmuster, Schachbrettmuster, Mäander, Zick-Zack-Muster). Selbst die diversen Kreuzformen basieren auf dem Rechten Winkel.
Siehe auch
Weblinks
- Eric W. Weisstein: Right Angle. In: MathWorld (englisch).
Einzelnachweise
- ↑ Clemens Thaer (Hrsg.): Die Elemente von Euklid (= Ostwalds Klassiker der exakten Wissenschaften. Band 235). Akademische Verlagsgesellschaft, Leipzig 1933.
- ↑ a b Johannes Tropfke: Geschichte der Elementarmathematik. Band 4: Ebene Geometrie. de Gruyter, Berlin 1940, ISBN 3-11-162150-2, S. 66 (Erstausgabe: 1903, Nachdruck).
- ↑ Hans-Joachim Schönknecht: Mythos – Wissenschaft – Philosophie: Zur Entstehung der okzidentalen Rationalität in der griechischen Antike Band 1-3; 2.4.1 Von der Praxis der Feldmessung zur mathematischen Geometrie, Tectum Wissenschaftsverlag, 2017, S. 98 ff. (eingeschränkte Vorschau in der Google-Buchsuche), abgerufen am 14. Mai 2020
- ↑ BGBl. 1970 I S. 981, 982, BGBl. 1973 I S. 1761
- ↑ Philipp Schrenk: Konstruktion eines rechten Winkels 2. (PDF) In: mathetreff-online. S. 1–2, abgerufen am 21. Juni 2025.
- ↑ Florian Cajori: A History of Mathematical Notations. Volume 1. Cosimo, 2013, ISBN 978-1-60206-685-4, S. 401.
- ↑ Matthias Fürderer: Die Kulturgeschichte des Rechten Winkels. (PDF; 811 kB) Fachhochschule Nordwestschweiz, Pädagogische Hochschule, 4. April 2008, archiviert vom (nicht mehr online verfügbar) am 31. März 2010; abgerufen am 10. Oktober 2008.Die Kulturgeschichte des Rechten Winkels. (PDF; 811 kB) (Nicht mehr online verfügbar.) Fachhochschule Nordwestschweiz, Pädagogische Hochschule, 4. April 2008, archiviert vom Original am 31. März 2010
Auf dieser Seite verwendete Medien
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Konstruktion des rechten Winkels als Animation
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Rechtwinkliges Dreieck
Autor/Urheber:
- Trigonometric_functions.svg: Alejo2083
- derivative work: Quartl
An image showing the trigonometric functions on 2d space: :Blue - Sine :Green - Cosine :Red - Tangent :Blue (dotted) - Cosecant :Green (dotted) - Secant :Red (dotted) - Cotangent
A - not totally accurate - computer graphic of a famous chair designed by Marcel Breuer and marketed by Knoll.
Autor/Urheber: Bernietaylor, Lizenz: CC BY-SA 3.0
Boxes possibly representing full moons and associated with (a) two ibexes, (b) a leaping cow, (c) a horse, and (d) above a horse. The first full moon is likely the one around the vernal equinox when these hunters arrived.
(c) I, Sakurambo, CC BY-SA 3.0
A right-handed three-dimensional Cartesian coordinate system with the +z axis pointing towards the viewer. Own work, produced as a replacement for 3D Cartesian coordinates.PNG
GRAPHING ERROR: It needs to be noted that this image is not an accurate depiction of an orthogonal 3-d coordinate system. Right angles, when rotated in the third dimension become projected as skewed. They no longer project as 90-degree angles as this image shows. A cube, for example, when looked at from one corner projects as a hexagon with 60-degree angles. According to this erroneous image, continuing rotation to the corner will result in a six-sided irregular hexagon that maintains a projection containing 90-degree angles. In other words, what is being depicted in this erroneous image is not a grid of orthogonal cubes, but rather skewed non-cubes that project their x-y plane faces as squares with 90-degree angles.
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Mittels Thaleskreis eine Senkrechte auf die Halbgerade h ab dem Punkt P errichten, der Punkt M ist frei wählbar, Animation
Autor/Urheber: Luigi Zanasi, Lizenz: CC BY-SA 2.0 ca
Picture of cabinetmaker's try square taken 18 September, 2005 by Luigi Zanasi (myself) on my workbench using a Olympus digital camera.
Autor/Urheber: Cobija, Lizenz: CC BY-SA 4.0
(translation) Göbeklitepe consists of buildings with a diameter of 30 meters and round and oval plan and georadar scans. The excavations of one of them were completed and the others were determined by geomagnetic and georadar methods. The results obtained with these measurements and excavations show that Göbeklitepe is a large meeting place of 11,500 years ago and it is covered with monumental buildings built for ceremonial purposes, not places for daily life. Among these monumental buildings, the most magnificent and preserved temple is the d temple. Temple D is dated to the first phase of the Göbeklitepe ruins (9500-8500 BC). In the center of the temple, with heights up to 6 meters and weights up to 30 tons; 12 steles were placed in the style of the center stelae. In the central steles, it is indisputable that the tiki post is depicted as the arm, hand, belt and garment, and the T steles symbolize the human or human-like saints. There are many animal depictions on the T steles in this temple. These are wild boars, wild oxen, donkeys gazelles, cranes, storks, ibis, ducks and feline as well as a large figure network of snakes and foxes are weighted.
Rechter Winkel markiert mit einem Punkt
Autor/Urheber: Peter Steinberg 23:04, 10. Feb. 2008 (CET), Lizenz: Copyrighted free use
Zeigt, wie mit Hilfe eines Geodreiecks eine Senkrechte zu einer gegebenen Geraden möglichst genau gezeichnet werden kann
(c) Bundesarchiv, Bild 183-09422-0001 / CC-BY-SA 3.0
Zwei lineare Funktionen, die sich in einem rechten Winkel schneiden
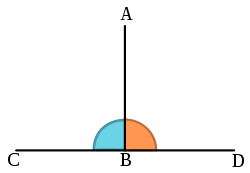

![Konstruktion eines rechten Winkels in einem Punkt '"`UNIQ--postMath-00000028-QINU`"', einer Halbgeraden '"`UNIQ--postMath-00000029-QINU`"', mithilfe des Thaleskreises (Punkt '"`UNIQ--postMath-0000002A-QINU`"' frei wählbar). Vorteilhaft, wenn Punkt '"`UNIQ--postMath-0000002B-QINU`"' auf oder nahe am Anfangspunkt '"`UNIQ--postMath-0000002C-QINU`"' liegt.[5]](http://upload.wikimedia.org/wikipedia/commons/d/df/01-Rechter_Winkel_mittels_Thaleskreis.gif)