Raumfüllung

Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion! (Artikel eintragen)

Eine Raumfüllung oder Parkettierung des dreidimensionalen Raumes ist das Ausfüllen des dreidimensionalen euklidischen Raumes mit dreidimensionalen Gebilden. Zweidimensionale Raumfüllungen nennt man Parkettierung.

Raumfüllungen können vollständig sein, d. h. das gesamte Volumen wird ausgefüllt, oder teilweise, was zu dem interessanten Problem der räumlich dichtesten Kugelpackung führt. In vielen praktischen Anwendungen ist man daran interessiert, die Dichte der Raumfüllung zu optimieren, zum Beispiel in der Verpackungsindustrie. Raumfüllungen mathematisch abstrahiert findet man u. a. bei den raumfüllenden Kurven, wo fraktale Gebilde mit einer fraktalen Dimension kleiner der Raumdimension n und größer als n − 1 zur Raumfüllung benutzt werden.

Raumfüllungen mit Polyedern

Raumfüllungen mit kongruenten Polyedern

Eine lückenlose Raumfüllung mit Polyedern wird auch als Parkettierung des dreidimensionalen Raumes bezeichnet. Es gibt genau fünf konvexe Polyeder, die nur durch regelmäßige Vielecke begrenzt sind, mit denen sich der Raum aus kongruenten Polyedern einer Art ausfüllen lässt:

• Würfel
• dreieckiges reguläres Prisma
• sechseckiges reguläres Prisma
• verdrehter Doppelkeil (Johnson-Körper J₂₆)
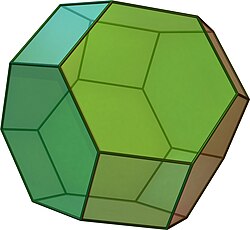
• Oktaederstumpf

Dabei enthalten die letzten vier Polyeder zwei Arten von Vielecken mit unterschiedlicher Eckenzahl. Unter den sogenannten Catalanischen Körpern ist lediglich das Rhombendodekaeder raumfüllend.^[1]

• 

  Würfel

• 

  Parallelepiped

• 

  dreieckiges reguläres Prisma

• 

  sechseckiges reguläres Prisma

• 

  Verdrehter Doppelkeil (Johnson-Körper J₂₆)

• 

  Verlängertes Rhombendodekaeder

• 

  Rhombendodekaeder

• 

  Oktaederstumpf

Jewgraf Stepanowitsch Fjodorow klassifizierte 1885 die raumfüllenden Paralleloeder, das heißt Polyeder, die sich durch Translation ineinander überführen lassen (affine Typen konvexer Paralleloeder), und fand im dreidimensionalen Raum fünf:^[2]

• 

  Parallelepiped

• 

  Hexagonales Prisma

• 

  Rhombendodekaeder

• 

  Verlängertes Rhombendodekaeder

• 

  Oktaederstumpf

Das wurde für seine Klassifikation kristallographischer Raumgruppen wichtig.

Raumfüllungen mit platonischen Körpern

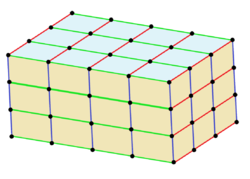
Es gibt zwei Raumfüllungen, die ausschließlich aus platonischen Körpern bestehen:

• 

  8 Würfel

• 

  8 Tetraeder und 6 Oktaeder

Raumfüllungen mit verschiedenen Polyedern

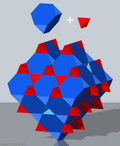
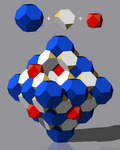
Folgende weitere Beispiele zeigen, wie der dreidimensionale Raum lückenlos mit platonischen Körpern, archimedischen Körpern oder catalanischen Körpern gleicher Kantenlänge ausgefüllt werden kann. Angegeben ist jeweils die Anzahl der Polyeder, die nötig ist, um einen vollen Raumwinkel von ${\displaystyle 4\cdot \pi \ \mathrm {sr} }$ zu bilden.

• 

  6 Tetraederstümpfe und 2 Tetraeder

• 

  4 Kuboktaeder und 2 Oktaeder

• 

  4 Hexaederstümpfe und 1 Oktaeder

• 

  1 Hexaederstumpf, 1 Rhombenkuboktaeder, 2 Achteckprismen und 1 Würfel

• 

  3 Rhombenkuboktaeder, 1 Würfel und 1 Tetraeder

• 

  2 Rhombenkuboktaeder, 2 Würfel und 1 Kuboktaeder

• 

  2 Oktaederstümpfe, 2 Tetraederstümpfe und 1 Kuboktaeder

• 

  2 Kuboktaederstümpfe und 2 Achteckprismen

• 

  2 Kuboktaederstümpfe, 1 Oktaederstumpf und 1 Würfel

• 

  2 Kuboktaederstümpfe, 1 Hexaederstumpf und 1 Tetraederstumpf

Kristallographische Restriktion

Bei periodischen Parkettierungen tritt ein interessantes Phänomen auf: Deren Symmetriegruppen können nur Drehungen um 360°, 180°, 120°, 90° oder 60° enthalten, also Elemente der Ordnungen 1, 2, 3, 4 und 6, jedoch keine Drehungen um andere Winkel, d. h. keine Elemente der Ordnungen 5, 7 oder höher. Diesen Sachverhalt, der übrigens auch für echte Kristalle gilt, bezeichnet man als kristallographische Restriktion. Die Ordnung 5 ist jedoch bei Quasikristallen möglich, die eine „fast“ periodische Teilung haben.

Siehe auch

• Voronoi-Diagramm
• Kristallgitter
• Parkettierung

Einzelnachweise

1. ↑ Wolfram MathWorld: Space-Filling Polyhedron
2. ↑ Eberhard Scholz, Symmetrie, Gruppe, Dualität, Birkhäuser 1989, S. 117