Rücktransport

In verschiedenen Teilgebieten der Mathematik bezeichnet man als Rücktransport^[1] oder Pullback (auch: Zurückziehung, Rückzug) Konstruktionen, die ausgehend von einer Abbildung ${\displaystyle f\colon X\to Y}$ und einem Objekt ${\displaystyle E}$, das in irgendeiner Weise zu ${\displaystyle Y}$ gehört, ein entsprechendes, „entlang von ${\displaystyle f}$ zurückgezogenes“ Objekt für ${\displaystyle X}$ liefern; es wird häufig mit ${\displaystyle f^{*}E}$ bezeichnet.

Das duale Konzept heißt meist Pushforward.

In der Kategorientheorie ist Pullback eine andere Bezeichnung für das Faserprodukt. Das duale Konzept wird hier Pushout, cokartesisches Quadrat oder Fasersumme genannt.

Sei ${\displaystyle f\colon M\to N}$ ein Diffeomorphismus zwischen glatten Mannigfaltigkeiten und sei ${\displaystyle \psi \colon N\to \mathbb {R} }$ eine glatte Funktion auf ${\displaystyle N}$. Dann ist der Rücktransport von ${\displaystyle \psi }$ bezüglich ${\displaystyle f}$ definiert durch

${\displaystyle f^{*}\colon C^{\infty }(N)\to C^{\infty }(M)}$ mit ${\displaystyle (f^{*}(\psi ))(x)=\psi (f(x))\,.}$

Der Rücktransport ${\displaystyle f^{*}\psi }$ ist also eine glatte Funktion ${\displaystyle M\to \mathbb {R} }$.

Schränkt man die Funktion ${\displaystyle \psi }$ auf eine offene Teilmenge ${\displaystyle U\subset N}$ ein, so erhält man ebenso eine glatte Funktion auf ${\displaystyle f^{-1}(U)\subset M}$. Der Rücktransport ist also ein Morphismus zwischen den Garben der glatten Funktionen von ${\displaystyle N}$ und ${\displaystyle M}$.

Seien ${\displaystyle M}$ und ${\displaystyle N}$ topologische Räume, ${\displaystyle \pi _{E}\colon E\to N}$ ein Vektorbündel über ${\displaystyle N}$ und ${\displaystyle f\colon M\to N}$ eine stetige Abbildung. Dann ist das zurückgezogene Vektorbündel ${\displaystyle \pi _{E'}\colon E'\to M}$ definiert durch

${\displaystyle E':=\{(x,e)\in M\times E|f(x)=\pi (e)\}}$

zusammen mit der Projektion ${\displaystyle \pi _{E'}(x,e):=x}$.^[2]

Es kann nun gezeigt werden, dass es einen Vektorbündelhomomorphismus ${\displaystyle f_{*}}$ gibt, so dass das Diagramm

${\displaystyle {\begin{array}{rcl}E'&{\stackrel {f_{*}}{\longrightarrow }}&E\\\pi _{E'}{\big \downarrow }&&{\big \downarrow }\pi _{E}\\M&{\stackrel {f}{\longrightarrow }}&N\end{array}}}$

kommutiert.^[2] Somit ist das zurückgezogene Vektorbündel ein Spezialfall eines Faserproduktes. Für einen fixierten Punkt ${\displaystyle p\in M}$ ist ${\displaystyle f_{*}|_{p}}$ eine lineare Abbildung zwischen Vektorräumen, daher gibt es eine duale Abbildung ${\displaystyle f^{*}|_{p}\colon E_{f(p)}^{*}N\to (E')_{p}^{*}}$. In diesem Kontext wird das zurückgezogene Vektorbündel ${\displaystyle E'}$ auch mittels ${\displaystyle f^{*}E}$ notiert und man nennt es auch Pullbackbündel von ${\displaystyle E}$ bezüglich ${\displaystyle f}$.

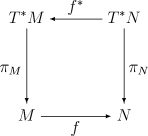
Im Bereich der Differentialgeometrie werden meist glatte Mannigfaltigkeiten anstatt beliebiger topologischer Räume ${\displaystyle M}$ und ${\displaystyle N}$ betrachtet. Dann wird auch zusätzlich gefordert, dass die Abbildung ${\displaystyle f\colon M\to N}$ und das Vektorbündel differenzierbar sind. Betrachtet man die entsprechenden Tangentialräume anstatt beliebiger Vektorbündel, so ist die Abbildung ${\displaystyle f_{*}}$ der Pushforward von ${\displaystyle f}$ und die zurückziehende Abbildung ${\displaystyle f^{*}\colon T_{f(p)}^{*}N\to T_{p}^{*}M}$ ist die duale Abbildung.^[3]

Ist ${\displaystyle \omega \in \Gamma (N,E)}$ ein Schnitt im Vektorbündel ${\displaystyle E}$, so ist ${\displaystyle f^{*}\omega \in \Gamma (M,f^{*}E)}$ der zurückgezogene Schnitt, der durch

${\displaystyle (f^{*}\omega )_{p}=\omega _{f(p)}}$

für alle ${\displaystyle p\in M}$ gegeben ist.

Im vorigen Abschnitt wurde der Rücktransport eines Schnitts in einem Vektorbündel definiert. In diesem Abschnitte werden konkrete Instanzen solcher Rücktransporte von Schnitten aufgeführt. Dazu sind in diesem Abschnitt ${\displaystyle M}$ und ${\displaystyle N}$ glatte Mannigfaltigkeiten und ${\displaystyle f\colon M\to N}$ eine glatte Abbildung.

Die Menge ${\displaystyle C^{\infty }(M)}$ der glatten Funktionen ${\displaystyle \psi \colon M\to \mathbb {R} }$ kann auf natürliche Weise mit dem Vektorraum ${\displaystyle \Gamma ^{\infty }(M,M\times \mathbb {R} )}$ der glatten Schnitte im Vektorbündel ${\displaystyle \textstyle \coprod _{p\in M}\mathbb {R} \cong M\times \mathbb {R} }$ identifiziert werden.^[4] Entsprechend kann der Rücktransport einer glatten Funktion ${\displaystyle (f^{*}(\psi ))(x)=\psi (f(x))}$ auch als Rücktransport eines glatten Schnittes des Vektorbündels ${\displaystyle M\times \mathbb {R} }$ aufgefasst werden.

Der Pushforward von ${\displaystyle f}$ entspricht gerade der äußeren Ableitung von ${\displaystyle f}$, was ein Vektorbündelhomomorphismus vom Tangentialraum ${\displaystyle TM}$ in den Tangentialraum ${\displaystyle TN}$ ist. Der duale Operator ${\displaystyle f^{*}}$ ist somit ein Bündelhomomorphismus vom Kotangentialbündel ${\displaystyle T^{*}N}$ in das Kotangentialbündel ${\displaystyle T^{*}M}$.

Sei ${\displaystyle \alpha }$ ein glatter Schnitt in ${\displaystyle T^{*}N}$, was per Definition eine 1-Form ist. Dann gilt für den Rücktransport von ${\displaystyle \alpha }$

${\displaystyle (f^{*}\alpha )_{p}(X)=\alpha _{f(p)}(df_{p}(X))}$

für ein ${\displaystyle p\in M}$.^[3]

Da die Menge der Differentialformen ein Vektorbündel bildet, kann man den Rücktransport einer Differentialform untersuchen.

Ist ${\displaystyle f\colon M\to N}$ eine differenzierbare Abbildung und ${\displaystyle \omega \in \Gamma (N,\Lambda ^{k}(T^{*}N))}$ eine k-Form auf ${\displaystyle N}$, so gilt für die auf ${\displaystyle M}$ zurückgezogene Differentialform ${\displaystyle f^{*}\omega }$ die Gleichung

${\displaystyle (f^{*}\omega )_{p}(X_{1},\ldots ,X_{k})=\omega _{f(p)}(f_{*p}X_{1},\ldots ,f_{*p}X_{k})}$

für Tangentialvektoren ${\displaystyle X\in T_{p}M}$ im Punkt ${\displaystyle p\in M}$ gegeben.^[5]

• R. Abraham, Jerrold E. Marsden, T. Ratiu: Manifolds, tensor analysis, and applications (= Applied mathematical sciences 75). 2. Auflage. Springer, New York NY u. a. 1988, ISBN 0-387-96790-7.

• Pullback einer Differentialform, nLab

1. ↑ Otto Forster: Riemannsche Flächen (= Heidelberger Taschenbücher 184). Springer, Berlin u. a. 1977, ISBN 3-540-08034-1. S. 62 (Englisch: Lectures on Riemann Surfaces (= Graduate Texts in Mathematics 81). Corrected 2nd printing. ebenda 1991, ISBN 3-540-90617-7).
2. ↑ ^{a b} Allen Hatcher: Vector Bundles & K-Theory. Version 2.1, May 2009, S. 18 online (PDF; 1,11 MB).
3. ↑ ^{a b} John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 136.
4. ↑ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 111.
5. ↑ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 303.