Röntgenbeugung

Röntgenbeugung, auch Röntgendiffraktion (englisch X-ray diffraction, XRD) genannt, ist die Beugung von Röntgenstrahlung an geordneten Strukturen wie Kristallen oder Quasikristallen. Grundsätzlich zeigt Röntgenstrahlung die gleichen Beugungserscheinungen wie Licht und alle anderen elektromagnetischen Wellen. Röntgenbeugung wird in der Materialphysik, der Kristallographie, der Chemie und der Biochemie eingesetzt, um die Struktur von Kristallen zu untersuchen, die sogenannte Röntgendiffraktometrie. Beispielsweise spielten Ergebnisse der Röntgenstreuung eine wichtige Rolle bei der Strukturanalyse der DNA. Die dazu eingesetzten Geräte waren ursprünglich Röntgenkameras, die Beugungsbilder auf handelsüblichen Röntgenfilmen festhielten, heute werden überwiegend Röntgendiffraktometer mit Zählrohren, Flächendetektoren o. ä. verwendet.
Geschichte
Das Phänomen der Röntgenbeugung an Kristallen wurde im Jahre 1912 von Max von Laue nach einem Gespräch mit Paul Peter Ewald[1] postuliert und durch die Versuche von Walter Friedrich und Paul Knipping bestätigt.[2] Von Laue erhielt dafür 1914 den Nobelpreis für Physik. Da Beugung eine typische Eigenschaft von Wellen ist, gelang es ihm so, die Wellennatur von Röntgenstrahlung nachzuweisen. Bis zu diesem Zeitpunkt war man sich noch nicht sicher, ob es sich bei der 1895 von Wilhelm Conrad Röntgen entdeckten Strahlung um Wellen oder Teilchen handelt. Heute weiß man, dass es sich bei Röntgenstrahlung um Licht mit Wellenlängen jenseits der UV-Strahlung handelt und diese sowohl Teilchen- als auch Welleneigenschaften besitzt (siehe Welle-Teilchen-Dualismus). Auf Grundlage der Arbeiten von Max von Laue begannen 1913 William Henry Bragg und William Lawrence Bragg (Vater und Sohn) die Röntgenbeugung als Verfahren zur Strukturaufklärung von Kristallen einzusetzen. Es gelang ihnen unter anderem, die Kristallstrukturen von NaCl, Diamant, Zinkblende, Flussspat und Calcit aufzuklären. Für diese Arbeiten erhielten beide im Jahre 1915 den Nobelpreis für Physik. Noch heute ist die Röntgenbeugung eines der Standardverfahren zur Strukturaufklärung von Festkörpern.[3][4]
Anwendungen
Die Anwendungsmöglichkeiten der Röntgenbeugung sind vielfältig. Neben Anwendungen in der Forschung werden Röntgenbeugungsmethoden in der Metall- und Baustoffindustrie, der pharmazeutischen Industrie oder der geologischen Erkundung routinemäßig und teilweise vollautomatisiert zur Probenuntersuchung oder Produktionsüberwachung eingesetzt. Zu den möglichen Anwendungen der Röntgenbeugung zählen:
- Phasenanalyse: die qualitative oder quantitative Bestimmung kristalliner Phasen anhand ihres Beugungsbildes, dazu gehört auch die Bestimmung von Mineralen
- Bestimmung der Gitterparameter (Gitterkonstanten)
- Kristallstrukturanalyse: die Bestimmung der Symmetrie (Raumgruppe) und die Kristallstrukturbestimmung im engeren Sinn, also die Bestimmung der Atompositionen innerhalb der Elementarzelle
- Röntgenographische Spannungsermittlung (RSE): Untersuchung des Dehnungs- und Spannungszustandes eines Materials
- Texturanalyse: die Bestimmung der Orientierungen (Orientierungsdichteverteilungsfunktion) der Kristallite in einem vielkristallinen Festkörper
- Bestimmung der Kristallorientierung bei Einkristallen
- Untersuchungen an dünnen Schichten
Für viele dieser Anwendungen wird neben klassischer Röntgenstrahlung heute auch Synchrotronstrahlung, Neutronenstrahlung oder Elektronenstrahlung eingesetzt.
Physikalischer Hintergrund
Beugung tritt auf, wenn der Abstand der Gitterlinien des Beugungsgitters in der Größenordnung der Wellenlänge der auftreffenden Wellen liegt. Die Wellenlänge von Röntgenstrahlen liegt in der Größenordnung von 1 pm bis 10 nm, was auch dem Abstand der Atome in Kristallen entspricht. Daher wirken diese auf Röntgenlicht wie ein dreidimensionales Beugungsgitter.
Die Röntgenstrahlung wird an der Elektronenhülle der bestrahlten Atome gebeugt (bei Neutronenstrahlung geschieht dies an den Nukleonen). Die so von den einzelnen Atomen ausgehenden gebeugten Wellen interferieren miteinander. Je nach Abstand der Atome untereinander ergeben sich für die gebeugten Wellen unterschiedliche Gangunterschiede. Ob es unter einem festen Winkel zu konstruktiver oder destruktiver Interferenz kommt, hängt daher vom Abstand der Atome untereinander ab.
Da Kristalle aus dreidimensionalen und periodisch angeordneten Struktureinheiten bestehen, tritt konstruktive Interferenz nur für ganz bestimmte Winkel auf. Diese Winkel lassen sich mittels der unten beschriebenen Bragg-Gleichung in Beziehung zu dem Abstand bestimmter Netzebenen des Kristalls setzen. Notwendige Bedingung für die Röntgenbeugung ist die Mosaikstruktur des Kristalls.
Eine Alternative zur Bragg-Beschreibung ist die Von-Laue-Beschreibung. Dort geht man nicht von Streuung an Netzebenen, sondern von Streuung an einzelnen mikroskopischen Objekten aus (siehe Hauptartikel Laue-Bedingung). Beide Beschreibungen sind, obwohl sie von unterschiedlichen Annahmen ausgehen, äquivalent.
Eine weitere Möglichkeit, die Röntgenbeugung durchzuführen, ist die direkte Erzeugung der Röntgenstrahlen im Kristall durch Anregung der Atome durch Beschuss mit hochenergetischen Teilchen (z. B. Elektronen). An der Beschreibung der Beugung durch die Bragg- oder Laue-Beschreibung ändert sich dabei nichts. Dies wird als Kossel-Effekt bezeichnet.[5]
Bragg-Gleichung

Die Bragg-Gleichung ist die zugrunde liegende mathematische Beziehung für die Ermittlung der Struktur aus dem bei der Röntgenbeugung erhaltenen Beugungsbild:
Dabei ist die Wellenlänge des monochromatischen Röntgenstrahls, mit dem man die Probe bestrahlt, der Abstand der Netzebenen, der Winkel zur Netzebene, unter dem die Strahlung auftrifft und der Grad des untersuchten Maximums von der Mitte aus, gezählt in Form einer natürlichen Zahl.
Die Gleichung beschreibt die Bedingungen für eine konstruktive Interferenz. Die rechte Seite der Bragg-Gleichung beschreibt den Gangunterschied zweier an zwei Netzebenen mit dem Abstand gebeugten Röntgenstrahlen. Beträgt dieser ein ganzzahliges Vielfaches der Wellenlänge, kommt es zu konstruktiver Interferenz. William Lawrence Bragg beschrieb diese Gleichung als „Reflexionsbedingung“, da makroskopisch der Eindruck entsteht, dass die Röntgenstrahlung vom Kristall unter dem Winkel reflektiert wird.
Wenn für eine Schar paralleler Netzebenen die Bragg-Gleichung erfüllt ist, überlagern sich die von den Einzelebenen „reflektierten“ Wellen also so, dass konstruktive Interferenz entsteht. Es gibt also für jede Netzebenenschar nur bestimmte Winkel, unter denen Reflexion stattfindet. Diese Winkel heißen Glanzwinkel oder Bragg-Winkel.
Die durch konstruktive Interferenz entstandene Strahlung kann von einem Detektor oder einem Fotofilm registriert werden. Der Ablenkungswinkel der aus konstruktiver Interferenz entstehenden Wellen vom einfallenden Strahl beträgt . Da die Wellenlänge der eingesetzten Röntgenstrahlung bekannt ist, lässt sich so der Netzebenenabstand berechnen, wobei hkl die Laue-Indizes sind, die die Lage der Schar paralleler Netzebenen im Kristallgitter und gleichzeitig die Beugungsordnung angeben.
Ist das Kristallsystem bekannt, kann man aus die Gitterkonstanten der kristallografischen Elementarzelle ableiten.
Im kubischen Kristallsystem gilt beispielsweise:
- .
Hat man errechnet, so lässt sich durch Zuordnen der Reflexe zu einzelnen Netzebenen (also zu hkl-Reflexen) die Gitterkonstante der Elementarzelle berechnen.
Für ein rhombisches Kristallsystem gilt:
- .
Hierbei erfolgt bei bekanntem d die Berechnung der Gitterkonstanten a, b und c durch Annäherungsverfahren. Ähnlich muss man für andere Kristallsysteme verfahren.
Wie bereits erwähnt, kommt es aufgrund der unterschiedlichen Netzebenenabstände zu miteinander interferierenden Röntgenstrahlen. Beim Eintritt in den Kristall sind die einzelnen Röntgenstrahlen in Phase. Aufgrund der Beugung kommt es jedoch zu Interferenz und einer Verschiebung der einzelnen Phasen untereinander, man spricht von Phasenbeziehungen. Die Bragg-Gleichung zeigt die Bedingung für eine konstruktive Interferenz. Die Phasenbeziehung ist damit eine Verschiebung der Phasen zweier Wellen um genau einen ganzzahligen Wert. Destruktive Interferenz resultiert bei Verschiebung der Phasen um nicht ganzzahlige Werte.
Mit Detektoren für Röntgenstrahlung kann nur die Intensität der Strahlung gemessen werden. Konstruktive bzw. destruktive Interferenz kann man aus erscheinenden Reflexen bzw. systematischen Auslöschungen erschließen. Alle anderen Phasenbeziehungen, die die eigentlichen Informationen für die Verteilung der Elektronendichte im Kristall tragen, gehen jedoch verloren. Dieses Dilemma ist in der Röntgenstrukturanalyse als das Phasenproblem bekannt.
Der Strukturfaktor ist die Gesamtresultierende aller in einer Richtung eines -Reflexes gebeugten Wellen. Die gemessene Intensität ist proportional zum Quadrat des Strukturfaktors ,
und der Strukturfaktor ist die Fourier-Transformation der Elektronendichte
- ,
wobei die Gitterkonstanten, die Koordinaten in der Elementarzelle und die Laue-Indizes darstellen. Den Positionen der Elektronendichtemaxima entsprechen dabei die Positionen der Atome in der Elementarzelle; Wasserstoffatome, bei denen das Maximum der Elektronendichte auf der Bindung zum Nachbaratom liegt, bilden die einzige Ausnahme.
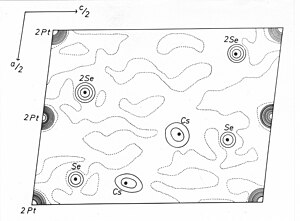
Die gemessenen Intensitäten besitzen nur Informationen über die Amplitude, also den Betrag des Strukturfaktors. Um aus den Intensitäten die Strukturfaktoren abzuleiten, muss deshalb das Phasenproblem gelöst werden. Heute werden dazu meist die „Direkten Methoden“ verwendet, für deren Entwicklung Herbert A. Hauptman und Jerome Karle 1985 den Nobelpreis für Chemie erhielten. Eine andere wichtige Methode zur Lösung des Phasenproblems ist die Patterson-Methode, die vor allem bei Anwesenheit von Schweratomen verwendet wird.
In der Praxis werden Fouriermethoden selten eingesetzt. Stattdessen verwendet man die Strukturverfeinerung. Der Strukturfaktor lässt sich auch ausdrücken als Summe aller atomaren Streufaktoren der Atome in der Elementarzelle:
- ,
wobei über alle Atome in der Elementarzelle summiert wird, die Koordinaten des Atoms und die Millerschen Indizes darstellen. Der atomare Streufaktor ist die Fourier-Transformation der Elektronendichte eines Atoms. Normalerweise wird dabei die Elektronendichte eines kugelförmigen Atoms angenommen, das nicht mit seinen Nachbaratomen überlappt. Mit Hilfe dieser Summengleichung lässt sich also der Strukturfaktor aus den Koordinaten der Atome in der Elementarzelle berechnen. In der Strukturverfeinerung verändert man nun das Strukturmodell (die Atomkoordinaten) solange, bis der Unterschied zwischen den experimentell gemessenen Strukturfaktoren und den aus dem Modell berechneten Strukturfaktoren minimal wird. Zur Strukturverfeinerung mit Computerprogrammen wird die Methode der kleinsten Quadrate eingesetzt.
Atome im Kristallgitter schwingen um ihre Ruheposition. Weil sich das auch auf die Reflexintensitäten auswirkt, werden die atomaren Streufaktoren für die thermische Bewegung korrigiert. Das Strukturmodell besteht folglich aus kugelförmigen Atomen, die um ihre Ruheposition (harmonisch) schwingen. Siehe Debye-Waller-Faktor.
Verfahren
Die ältesten Beugungsverfahren sind das Laue-Verfahren (1912), die Bragg’sche Spektrometermethode (1913),[6] das Debye-Scherrer-Verfahren (1916)[7][8] und das Drehkristallverfahren, das nach ersten Ansätzen von Maurice de Broglie von Michael Polanyi und Karl Weissenberg sowie unabhängig davon von Ernst Schiebold entwickelt wurde.[9] Aus diesen vier ursprünglichen Verfahren ging eine Vielzahl weiterer Verfahren und Geräte hervor, die nach folgenden Kriterien eingeteilt werden können: verwendete Strahlung („weiß“ oder monochromatisch), Probe (Einkristall oder Pulver) und Detektor (Film oder Zählrohr).[10]
| Strahlung | Probe | Detektor | Verfahren |
|---|---|---|---|
| weiß | Einkristall | Film | Laue-Kamera |
| Zählrohr (Ionisationskammer) | Bragg-Spektrometer | ||
| monochromatisch | Einkristall | Film | Drehkristall-Kamera, Schwenkaufnahmen (oscillating camera) Weissenberg-Kamera De Jong-Bouman-Kamera Präzessions-Kamera |
| Zählrohr, auch Flächendetektoren | Einkristalldiffraktometer | ||
| monochromatisch | Pulver | Film | Debye-Scherrer-Kamera Guinier-Kamera Seemann-Bohlin-Kamera Gandolfi-Kamera |
| Zählrohr | Pulverdiffraktometer (meist Bragg-Brentano-Diffraktometer) Guinier-Diffraktometer |
Laue-Verfahren
Im Laue-Verfahren wird ein Einkristall polychromatischer Röntgenstrahlung ausgesetzt. Die Idee ist, die Bragg-Gleichung durch Variation der Wellenlängen zu erfüllen. Die im Beugungsbild erhaltenen Reflexe sind jedoch nicht eindeutig einzelnen Netzebenenabständen zuzuordnen. Es wird heute noch zur Untersuchung dynamischer Prozesse, beispielsweise in Proteinkristallen verwendet.
Drehkristall-Verfahren
Eine Auswertung des Laue-Verfahrens zur Bestimmung von nach der Bragg-Gleichung ist kaum möglich. Ebenso können die Gitterkonstanten nicht bestimmt werden. Beim Drehkristallverfahren wird der zu untersuchende Einkristall um eine Zonenachse senkrecht zum Primärstrahl gedreht. Die Auswertung der Drehkristallaufnahme ermöglicht es, und die Gitterkonstanten zu ermitteln.
Weissenberg-Verfahren
Dieses Verfahren ist eine Weiterentwicklung des Drehkristallverfahrens.[11] Dazu wird eine zylinderförmige Schichtlinienblende zwischen Kristall und Film in die Kamera eingebracht. Diese bewirkt, dass nur die Strahlen eines Lauekegels, dessen Öffnungswinkel durch Verschieben der Blende einstellbar ist, den Film belichten können. Zusätzlich wird die Kristalldrehung synchron mit einer Linearverschiebung des zylindrisch gerollten Films gekoppelt (z. B. 1° Kristalldrehung entspricht einer Filmbewegung von 1 mm). Dadurch werden die Reflexe in der Filmebene auseinandergezogen, womit es einfacher ist, die Indizes der einzelnen Reflexe zu bestimmen. Die Weissenberg-Aufnahme zeigt anstelle des Primärflecks bei der Drehkristallaufnahme eine Mittellinie, von der aus jedem Reflex zwei Koordinaten zugewiesen werden können.
Zwei ähnliche Verfahren, bei denen der Film nicht verschoben, sondern um die Achse des Primärstrahls gedreht wird, sind die Verfahren von Erwin Sauter[12] und Ernst Schiebold.[13] Diese beiden Verfahren, die oft unter der Bezeichnung Schiebold-Sauter-Verfahren zusammengefasst werden, wurden im Gegensatz zum Weissenberg-Verfahren in der Praxis wenig verwendet.
Debye-Scherrer-Verfahren

Das von Peter Debye und Paul Scherrer sowie unabhängig davon von Albert W. Hull entwickelte Verfahren arbeitet nicht mit Einkristallen, sondern mit pulverförmigen Proben. Das Pulver besteht aus einer Reihe zufällig angeordneter Kristallite, so dass auch die Netzebenen zufällig im Raum angeordnet sind und so einige immer die Bragg’sche Reflexionsbedingung erfüllen. Zusätzlich rotiert die Probe um eine Achse senkrecht zum einfallenden Strahl. Um die Probe bilden sich Kegelmäntel aus Röntgenstrahlen, welche aus der konstruktiven Interferenz stammen. Um die Probe liegt ein fotografischer Film, auf dem sich die Kegelmäntel als Reflexe abzeichnen, aus denen sich dann das Diffraktogramm erstellen lässt. Aus den Abständen der vom einfallenden Strahl auf dem Film aufgenommenen Reflexe lässt sich der Glanzwinkel errechnen:
- .
Der Abstand des Beugungsreflexes auf dem Film vom einfallenden Strahl verhält sich zum Umfang der Kamera wie der Öffnungswinkel des entsprechenden Beugungskegels zu 360°.
Verfahren nach Guinier
Dieses Verfahren ähnelt dem Debye-Scherrer-Verfahren. In einer kreisförmigen Kammer wird die Probe allerdings nicht in der Mitte angebracht, sondern wie der Film an der Kammerwand. Es lässt sich zeigen, dass jeder Strahl, der die Kammer durchquert und auf denselben Punkt auf einer Wand fokussiert ist, bei der Beugung an der anderen Wand auf den gleichen Punkt auf dem Kreisumfang abgebildet wird. So kann ein Röntgenstrahl benutzt werden, der nicht parallelisiert, sondern nur durch streifenden Einfall in einen Hohlspiegel fokussiert ist. Damit kann die Intensität einer Röntgenquelle mit einfachen Mitteln wesentlich besser ausgenutzt werden.
Man kann mit der Kammer Durch- und Rückstrahlungsaufnahmen herstellen. Der Abstand der Reflexe auf dem Film ist wie bei der Debye-Scherrer-Methode direkt proportional zum Beugungswinkel. Der Durchmesser der Kammer beträgt üblicherweise 114,7 mm. Beim Ausmessen der Beugungsmuster auf dem Film entspricht dann 1 mm genau 0,5°. Mit dieser Methode erhält man schärfer abgebildete Beugungsringe. Außerdem können gleichzeitig drei Präparate in Pulverform aufgenommen werden, wobei man in der Regel zwei Präparate mit einer Kalibriersubstanz, die auf dem Film im mittleren Bereich abgebildet wird, aufnimmt.[14][15]
Zählrohrverfahren
In modernen Pulverdiffraktometern wird anders als in den vorigen Verfahren zur Registrierung der gebeugten Röntgenstrahlen statt eines Films ein Szintillationszähler benutzt, der die Funktion eines Zählrohrs besitzt. Mit diesem Verfahren kann die Interferenzintensität mit hoher Genauigkeit direkt bestimmt werden. Ein weiterer Vorteil ist die digitale Auswertung, sodass viele Arbeitsschritte automatisiert werden können.
Einkristalldiffraktometer verwenden entweder ebenfalls einen solchen Punktdetektor oder einen Flächendetektor (CCD, CMOS, Imageplate), der gleichzeitig die Intensität und Form mehrerer Reflexe vermessen kann.
Andere Methoden
Eine besondere Form der Röntgenstreuung ist die Kleinwinkelstreuung (engl. small angle X-ray scattering, SAXS): Da gemäß der Bragg-Gleichung bei vorgegebener Wellenlänge größere Strukturen einen kleineren Streuwinkel zur Folge haben, kann die Kleinwinkelstreuung eingesetzt werden, um mesoskopische Strukturen wie Kolloide, teilkristalline Polymere und dergleichen zu untersuchen. SAXS ist eine der Standardmethoden zur Strukturaufklärung in der Soft-Matter-Physik.
Eine weitere Form der Röntgenstreuung ist WAXS (engl. wide angle X-ray scattering, Weitwinkel-Röntgenstreuung).
Als Röntgenquellen dienen Röntgenröhren und Synchrotrons. Alternativ (und ergänzend) zur Röntgenstreuung werden Neutronenstreuung und Elektronenbeugung eingesetzt. Der Vorteil der Strukturbestimmung mit Synchrotronstrahlung liegt in der hohen Intensität und der exzellenten vertikalen Kollimation. Die Auswertung von Pulverdaten wird durch die höhere Auflösung wesentlich erleichtert.
Für Dünne Schichten ist die Röntgendiffraktometrie mit streifendem Einfall besonders geeignet.
Durch AXS (engl. anomalous X-ray scattering, anomale Röntgenstreuung) kann in Röntgen-Streuexperimenten der Kontrast zwischen mehreren in der Probe enthaltenen Elementen erhöht werden. Dabei wird ausgenutzt, dass der Formfaktor eines Elements eine ausgeprägte Abhängigkeit von der Wellenlänge der einfallenden Strahlung aufweist, wenn diese in der unmittelbaren Nähe einer Absorptionskante jenes Elements liegt. Bei Anwenden dieser Technik können zusätzliche Informationen zu Elementen erhalten werden, die in einem regulären Streuexperiment wenig zur gestreuten Intensität beitragen würden, weil 1. das gefragte Element eine geringere Ordnungszahl besitzt als andere Probenbestandteile, oder 2. weil die Konzentration des Elements in der Probe sehr gering ist. Da für AXS die Wellenlänge der Strahlung variiert werden muss und die zu beobachtenden Effekte schwach sind, wird für solche Messungen meist Synchrotronstrahlung genutzt.
Röntgenbeugung in Flüssigkeiten

Beobachtet man bei festen kristallinen Stoffen scharfe Reflexe, die unter ganz bestimmen Glanzwinkeln auftreten und auf die Netzebenen im Kristall zurückzuführen sind, so weist das Beugungsdiagramm von Flüssigkeiten in der Intensivitätsverteilung breite und wenig strukturierte Maxima auf. Trotz der geringen Strukturierung der Beugungsdiagramme von Flüssigkeiten lassen sich zumindest im Nahordnungsbereich innerhalb eines Clusters bestimmte Aussagen machen. Über die Intensivitätsverteilung lassen sich Abstandsvektoren der Teilchen, also Aussagen über Abstände und Richtungen, wie in einem Kristall nicht bestimmen, sondern nur ihre Beträge. Man erhält eine Abstandsstatistik, die eine Verteilungsfunktion der Paarabstände beschreibt. Insofern ist es ein Problem eine dreidimensionale Struktur abzuleiten. Über indirekte Verfahren lassen sich aber mit Strukturmodellen und deren berechnete Abstandsstatistiken und einem Vergleich mit der experimentellen Paarverteilungsfunktion Aussagen über eine mögliche Struktur treffen. So war es gelungen von der Röntgenstrukturuntersuchung des hexagonalen Eises mit einer β-Tridymitstruktur Rückschlüsse auf flüssiges Wasser zu ziehen. Ein hexagonales Strukturmodell lieferte gute Übereinstimmungen mit den experimentellen Daten, sodass man in Wasserclustern ebenfalls eine β-Tridymitstruktur annahm. Beispielsweise führten Röntgenstrukturuntersuchungen einer wässrigen Cäsiumfluoridlösung zu der Folgerung, dass bei der Hydratation von Cäsiumionen diese sich in die β-Tridymitstruktur der Wassercluster einlagern.
Bereits Ende der 1920er Jahre wurden Röntgenbeugungen mit Flüssigkeiten von Peter Debye, Frits Zernike und anderen durchgeführt. Eine Ermittlung von Strukturen im Nahordnungsbereich war mit den damaligen Hilfsmitteln wegen des hohen Rechenaufwandes jedoch noch nicht möglich und wurde erst mit dem Einsatz von Computern interessant.
Siehe auch
Literatur
- Herbert Zimmermann: Röntgenstrukturuntersuchung von Flüssigkeiten. In: Chemie in unserer Zeit, 9. Jahrg. 1975, Nr. 4, S. 99–107.
- Walter Borchardt-Ott: Kristallographie: eine Einführung für Naturwissenschaftler. Verlag Springer, Berlin 1997, ISBN 3-540-63044-9.
- Werner Massa: Kristallstrukturbestimmung. Verlag Teubner, Stuttgart 2002, ISBN 3-519-23527-7.
- Rudolf Allmann: Röntgenpulverdiffraktometrie. Verlag Springer, Berlin 2003, ISBN 3-540-43967-6.
- E. Prince (Hrsg.): International Tables for Crystallography (third series). Volume C. Mathematical, physical and chemical tables. 3. Auflage. Springer, 2004, ISBN 978-1-4020-1900-5 (eingeschränkte Vorschau in der Google-Buchsuche).
- Lothar Spieß, Gerd Teichert, Robert Schwarzer, Herfried Behnken, Christoph Genzel: Moderne Röntgenbeugung: Röntgendiffraktometrie für Materialwissenschaftler, Physiker und Chemiker. 3. Auflage. Springer Spektrum, Wiesbaden 2019, ISBN 978-3-8348-1219-3, S. 635 (eingeschränkte Vorschau in der Google-Buchsuche).
Weblinks
- LP - Röntgenbeugung (inkl. Skizzen, Fotos, Videos und Literaturhinweisen)
- Grundlagen der Röntgen-Diffraktometrie (XRD) und Röntgen-Pulverdiffraktometrie (XRPD) (PDF, 2,7 MB)
- XRD bei Terrachem - Bestimmung der kristallinen Struktur von verschiedenen Probenmaterialien
Einzelnachweise
- ↑ Wolfgang Neumann, Klaus-Werner Benz: Kristalle Verändern Unsere Welt Struktur - Eigenschaften - Anwendungen. Walter de Gruyter GmbH & Co KG, 2018, ISBN 978-3-11-043907-6, S. 65 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Horst Biermann, Lutz Krüger: Moderne Methoden der Werkstoffprüfung. John Wiley & Sons, 2014, ISBN 978-3-527-67070-3, S. 255 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Lothar Spieß, Robert Schwarzer, Herfried Behnken, Gerd Teichert: Moderne Röntgenbeugung Röntgendiffraktometrie für Materialwissenschaftler, Physiker und Chemiker. Springer-Verlag, 2015, ISBN 978-3-663-10831-3 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Ludwig Bergmann, Clemens Schaefer: Lehrbuch der Experimentalphysik - 6. Festkörper. Walter de Gruyter, 2005, ISBN 978-3-11-017485-4, S. 112 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Kossel-Effekt im Techniklexikon
- ↑ W. H. Bragg, W. L. Bragg: The Reflection of X-rays by Crystals. In: Proceedings of the Royal Society of London. Series A. Band 88, Nr. 605, 7. Januar 1913, S. 428–438, doi:10.1098/rspa.1913.0040.
- ↑ Peter Debye, Paul Scherrer: Interferenzen an regellos orientierten Teilchen im Röntgenlicht. I. In: Nachr. Ges. Wiss. Göttingen, Mathematisch-Physikalische Klasse. 1916, S. 1–15.
- ↑ Peter Debye, Paul Scherrer: Interferenzen an regellos orientierten Teilchen im Röntgenlicht. II. In: Nachr. Ges. Wiss. Göttingen, Mathematisch-Physikalische Klasse. 1916, S. 16–26.
- ↑ Michael Polanyi, Ernst Schiebold, Karl Weissenberg: über die Entwicklung des Drehkristallverfahrens. In: Zeitschrift für Physik. Band 23, Nr. 1, Dezember 1924, S. 337–340, doi:10.1007/BF01327599.
- ↑ Diffraction techniques in the solid state. ( vom 3. Oktober 2013 im Internet Archive) (PDF; 930 kB) Vorlesungsskript, University of Lethbridge.
- ↑ Karl Weissenberg: Ein neues Röntgengoniometer. In: Zeitschrift für Physik. Band 23, Nr. 1, Dezember 1924, S. 229–238, doi:10.1007/BF01327586.
- ↑ Erwin Sauter: Eine einfache Universalkamera für Röntgen-Kristallstrukturanalysen. In: Zeitschrift für Kristallographie. Band 85, 1933, S. 156–159.
- ↑ Ernst Schiebold: Über ein neues Röntgengoniometer. Gleichzeitig Bemerkung zu der Arbeit von E. Sauter; „Eine einfache Universalkamera für Röntgen-kristallstrukturanalysen“. In: Zeitschrift für Kristallographie. Band 86, 1933, S. 370–377 und 377–383.
- ↑ W. Bronger: Röntgenographische Untersuchungen nach der Pulvermethode. Schrift des Instituts für Anorganische Chemie der RWTH Aachen 1971.
- ↑ W. Kleber: Einführung in die Kristallographie. VEB Verlag Technik Berlin 1969, S. 344.
Auf dieser Seite verwendete Medien
Bragg-Beugung
Autor/Urheber: Johannes Schneider, Lizenz: CC BY-SA 4.0
Schema der Untersuchung der Röntgenbeugung in einer Flüssigkeit
(c) Martinl, CC BY-SA 3.0
Elektronendichte von Maleinsäureanhydrid. Messtemperatur 130 K. Auflösung d = 0,54 Å. Kontourlinien gezeichnet mit 2,5 e/Å3.
Autor/Urheber: Thomas Splettstoesser (www.scistyle.com), Lizenz: CC BY-SA 3.0
Structure determination by X-ray crystallography
Elektronendichten über Fouriertransformation eines Cäsiumselenoplatinats mit Zuordnung der Cs-, Pt- und Se-Atome
Pulveraufnahmen nach Debye-Scherrer (oben) und Guinier (unten) für ein Kaliumthioplatinat






