Quadratzahl

Eine Quadratzahl oder Viereckszahl ist eine Zahl, die durch Quadrieren einer ganzen Zahl, also die Multiplikation einer solchen mit sich selbst, entsteht. Beispielsweise ist eine Quadratzahl. Die ersten Quadratzahlen sind
- 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, … (Folge A000290 in OEIS)
Einige Mathematiker sehen die Null nicht als Quadratzahl; sie beginnen diese Zahlenfolge mit der Eins.
Die Bezeichnung Quadratzahl leitet sich von der geometrischen Figur des Quadrats her. Die Anzahl der Steine, die man zum Legen eines Quadrats benötigt, ist immer eine Quadratzahl. So lässt sich beispielsweise mit 16 Steinen ein Quadrat mit der Seitenlänge 4 legen.
Aufgrund ihrer Verwandtschaft mit einer geometrischen Figur zählen die Quadratzahlen zu den figurierten Zahlen, zu denen auch die Dreieckszahlen und Kubikzahlen gehören. Diese Begriffe waren schon den griechischen Mathematikern der Antike bekannt.[1]
Die Quadratzahlen zählen – ebenso wie die Dreieckszahlen – insbesondere auch zu den Polygonalzahlen.[2]
Eigenschaften
Eine Quadratzahl ist genau dann eine gerade Zahl, wenn ihre Basis gerade ist. Allgemeiner gilt: Eine Quadratzahl ist genau dann durch eine Primzahl teilbar, wenn ihre Basis durch teilbar ist.
Rekursion
Bezeichnet man die Folge der Quadratzahlen mit , so hat man die folgende Rekursionsvorschrift:[2]
Formeln zum Generieren von Quadratzahlen
Jede Quadratzahl ist die Summe der ersten ungeraden natürlichen Zahlen.
Diese Gesetzmäßigkeit, in englischsprachiger Literatur auch als Odd Number Theorem bekannt,[3] wird durch die folgenden Bilder veranschaulicht.
 |  | ||
Von links nach rechts sind hier die ersten vier Quadratzahlen durch die entsprechende Anzahl an Kugeln dargestellt. Die blauen Kugeln zeigen jeweils den Unterschied zur vorhergehenden Quadratzahl an. Da von links nach rechts immer eine Reihe und eine Spalte hinzukommt, erhöht sich die Anzahl der blauen Kugeln jeweils um 2. Beginnend mit der 1 ganz links durchlaufen so die blauen Kugeln alle ungeraden Zahlen.
Das Bildungsgesetz
lässt sich induktiv beweisen. Der Induktionsanfang
folgt aus dem offensichtlichen und
Aus der Induktionsvoraussetzung
folgt wegen der binomischen Formel und
sofort die Induktionsbehauptung
Außerdem ist jede Quadratzahl die doppelte Summe der ersten natürlichen Zahlen plus der Zahl :
Beispiele:
Dies lässt sich auch leicht geometrisch veranschaulichen: In dem aus Kugeln gelegten Quadrat liegen auf einer der Diagonalen Kugeln, diesseits und jenseits von ihr je .
Geometrische Generierung
In der Quadratzahl ist die Basis eine reelle Zahl und der Exponent eine positive ganze Zahl. Aus diesem Grund ist der Potenzwert von auf einer Zahlengeraden als Konstruktion mit Zirkel und Lineal darstellbar.
Es ist zu unterscheiden, ob die Basis größer oder kleiner als die Zahl ist. Im Folgenden werden beide Möglichkeiten beschrieben.
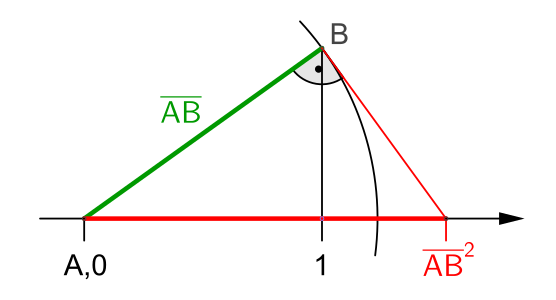
Vorgehensweise für Basis > 1
- Ziehe auf der Zahlengeraden einen Kreisbogen mit Mittelpunkt und der Basis als Radius.
- Bestimme den Abstand mit der Länge zum Punkt und errichte eine Senkrechte zur Zahlengeraden im Punkt , bis sie den Kreisbogen in schneidet.
- Errichte eine Senkrechte zur Basis im Punkt , bis sie die Zahlengerade in schneidet.
- Konstruktion der Quadratzahl mit Basis
- Konstruktion der Quadratzahl mit Basis
Vorgehensweise für Basis < 1
- Bestimme auf der Zahlengeraden die Basis als Strecke mit .
- Bestimme auf der Zahlengeraden ab die Strecke mit der Länge und konstruiere einen Halbkreis um .
- Ziehe einen Kreisbogen um mit dem Radius , bis er den Halbkreis in schneidet.
- Das abschließende Lot von auf die Zahlengerade liefert als Fußpunkt die Quadratzahl .
Trick zum Berechnen des Quadrats einer Zahl mit Einerziffer 5
Das Quadrat von Zahlen, die auf 5 enden (die sich also in der Form mit einer natürlichen Zahl darstellen lassen), lässt sich leicht im Kopf berechnen. Man multipliziert die Zahl ohne die Einerziffer 5 (z. B. bei 65 die 6) mit ihrem Nachfolger (hier 6 + 1 = 7) und hängt an das Produkt (hier 6 · 7 = 42) die Ziffern 2 und 5 an (Endergebnis 4225).
Beweis:
Beziehungen zu anderen figurierten Zahlen
Dreieckszahlen

Jede Quadratzahl lässt sich als Summe zweier aufeinanderfolgender Dreieckszahlen darstellen. Das nebenstehende Bild zeigt beispielhaft, wie sich die Quadratzahl 25 als Summe der Dreieckszahlen und ergibt.
Dieses Phänomen lässt sich auch durch eine Formel beschreiben.
Jede ungerade Quadratzahl lässt sich als Nachfolger einer 8-fachen Dreieckszahl darstellen.
Beweis: mit
Zentrierte Quadratzahlen
Neben dem den Quadratzahlen zugrundeliegenden Muster gibt es noch ein zweites Muster, um ein Quadrat zu legen. Dabei werden um einen Stein in der Mitte des Quadrats weitere Quadrate gelegt. Die für diese Muster notwendige Anzahl an Steinen entspricht jeweils einer zentrierten Quadratzahl. Jede zentrierte Quadratzahl ist die Summe zweier aufeinanderfolgender Quadratzahlen, wie sich an deren geometrischem Muster erkennen lässt.
Der Term für zentrierte Quadratzahlen lässt sich mit Hilfe der binomischen Formel so umstellen, dass die beiden Quadratzahlen sichtbar werden:
Pyramidenzahlen
Die Summe der ersten Quadratzahlen ergibt die -te Pyramidenzahl:
Das folgende Bild veranschaulicht diese Beziehung am Beispiel der vierten Pyramidenzahl.
Endziffern von Quadratzahlen
Quadratzahlen enden nie mit einer der Ziffern 2, 3, 7 oder 8, da kein Quadrat einer einstelligen Zahl mit einer dieser Ziffern endet.
Ist die letzte Ziffer einer beliebigen Zahl , dann gilt für deren Quadrat
Die letzte Ziffer von ist somit identisch mit der letzten Ziffer von . Unter den zehn Quadraten 0, 1, 4, 9, 16, 25, 36, 49, 64 und 81 aller Ziffern findet sich jedoch keines, das auf 2, 3, 7 oder 8 endet.
Symmetrie in den beiden Endziffern um die Basis 25
Die Quadratzahlen sind um die Basis 25 herum in den beiden Endziffern symmetrisch:
Das erklärt sich wie folgt: Für jede natürliche Zahl gilt:
Da die Differenz also ein Vielfaches von ist, sind die beiden Endziffern gleich.
Restklassen von Quadratzahlen
Die vorherige Aussage über mögliche Endziffern von Quadratzahlen bedeutet, dass die möglichen Restklassen der Quadratzahlen modulo repräsentieren. Auch für andere Zahlen sind die Restklassen der Quadratzahlen modulo immer nur ein Teil der insgesamt möglichen Restklassen. Für sind beispielsweise die möglichen Restklassen der Quadratzahlen . Insbesondere sind die Restklassen sowohl der Quadrate modulo als auch modulo und sind die Restklassen der Quadrate modulo . Daraus folgt beispielsweise sowohl, dass keine Restklasse der Summe zweier Quadratzahlen modulo ist, als auch, dass keine Restklasse der Summe dreier Quadratzahlen modulo ist.
In der elementaren Zahlentheorie spielen Untersuchungen über quadratische Reste eine wichtige Rolle.
Teileranzahl
Nur Quadratzahlen haben eine ungerade Anzahl von Teilern. Beweis: Sei , und . Es ist , denn . enthält alle Teiler von , also ist die Anzahl der Teiler von gleich . Ist eine Quadratzahl, so ist . Andernfalls ist .
Reihe der Kehrwerte
Die Summe der Kehrwerte aller Quadratzahlen ist
- .
Es war lange Zeit nicht bekannt, ob diese Reihe konvergiert, und wenn ja, gegen welchen Grenzwert. Erst Leonhard Euler fand im Jahr 1735 den Wert der Reihe.
Summen zweier aufeinanderfolgender Quadratzahlen
Mit der Dreieckszahl gilt die Identität: .
Summen aufeinanderfolgender Quadratzahlen
Es gibt einige merkwürdige Beziehungen für die Summe aufeinanderfolgender Quadratzahlen:
oder allgemein
Manche Primzahlen lassen sich als Summe von zwei, drei oder gar sechs aufeinanderfolgenden Quadraten schreiben (andere Anzahlen an Summanden sind nicht möglich):
- :
- :
- :
Literatur
- Peter Bundschuh: Einführung in die Zahlentheorie (= Springer-Lehrbuch). Dritte, vollständig überarbeitet Auflage. Springer-Verlag, Berlin, Heidelberg 1996, ISBN 3-540-60920-2.
- Emil Grosswald: Representations of Integers as Sums of Squares. Springer-Verlag, New York / Berlin / Heidelberg / Tokio 1985, ISBN 0-387-96126-7 (MR0803155).
- Harald Scheid, Wolfgang Schwarz: Elemente der Arithmetik und Algebra. 6. Auflage. Springer Spektrum, Heidelberg, Berlin 2016, ISBN 978-3-662-48773-0, doi:10.1007/978-3-662-48774-7.
Siehe auch
Weblinks
Einzelnachweise
- ↑ Helmuth Gericke: Mathematik in Antike, Orient und Abendland. Marix Verlag, Wiesbaden 2005, ISBN 3-937715-71-1, S. 142–143.
- ↑ a b Harald Scheid, Wolfgang Schwarz: Elemente der Arithmetik und Algebra, 2016, S. 90ff.
- ↑ Eric W. Weisstein: Odd Number Theorem. In: MathWorld (englisch).
Auf dieser Seite verwendete Medien
Autor/Urheber: Stefan Friedrich Birkner, Lizenz: CC BY-SA 3.0
The Square Number 1 with the Gnomon 1
The Square Number 9 with its Gnomon
Autor/Urheber: Stefan Friedrich Birkner, Lizenz: CC BY-SA 3.0
16 Kugeln, angeordnet als Summe von Gnomonen von Quadraten.
Autor/Urheber: Stefan Friedrich Birkner, Lizenz: CC BY-SA 3.0
The square number 25 as sum of the triangular numbers 10 and 15.
Autor/Urheber: Stefan Friedrich Birkner, Lizenz: CC BY-SA 3.0
The Square Number 16 with its Gnomon
Autor/Urheber: Stefan Friedrich Birkner, Lizenz: CC BY-SA 3.0
Decomposition of the centered square number 13 into the square numbers 9 and 4.
The Square Number 4 with its Gnomon
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Quadrieren einer Strecke bzw. einer Zahl < 1
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Quadrieren einer Strecke bzw. einer Zahl > 1