Quadratur des Quadrates

[1] Einfache, perfekte Quadratur der geringstmöglichen Ordnung (21)

Unter der Quadratur des Quadrates versteht man die lückenlose und überlappungsfreie Bedeckung („Parkettierung“) eines gegebenen Quadrates mit kleineren Quadraten, deren Seitenlängen ganzzahlige Werte haben. Die Bezeichnung Quadratur des Quadrates wurde in scherzhafter Anlehnung an die Quadratur des Kreises gewählt,^[1] obwohl die beiden Problemstellungen nichts miteinander zu tun haben.

Eigenschaften

[2] Einfache, unperfekte Quadratur der geringstmöglichen Ordnung (13)

[3] Perfekte, zusammengesetzte Quadratur der Ordnung 24

Seitenlängen

Der deutsche Geometer Max Dehn bewies 1903, dass die Seiten eines mit Quadraten parkettierten Rechteckes (also auch die eines Quadrates) mit den Seiten der Teilquadrate kommensurabel sein müssen. Dies bedeutet, dass die Seitenlängen des quadrierten Rechtecks und die aller Teilquadrate ganzzahlige Vielfache einer einzigen Zahl sind; bei geeigneter Wahl der Längeneinheit sind dann alle Seitenlängen ganze Zahlen.^[2]

Ordnung

Als Ordnung (engl. order) einer Parkettierung bezeichnet man die Zahl der Teilquadrate.^[3]

Zusatzbedingungen

Triviale Beispiele für die Parkettierung von und mit Quadraten finden sich in vielen Dingen des Alltags – wie etwa dem Schachbrett oder an jeder mit quadratischen Kacheln gefliesten Küchenwand. Interessant und anspruchsvoll wird die Aufgabenstellung durch folgende Zusatzbedingungen:

• Keine zwei Teilquadrate sollen die gleiche Größe haben. Eine Quadrat-Parkettierung, die diese Bedingung erfüllt, heißt perfekt.^[3]
• Solange eine Teilmenge der Teilquadrate ein Rechteck bildet, heißt die Quadratur zusammengesetzt (engl. compound), andernfalls – dies ist der schwierigere Fall – einfach (engl. simple).^[3]

Für unperfekte Parkettierungen, also solche, die mehrere kongruente Teilquadrate enthalten, werden weitere Zusatzbedingungen betrachtet:^[1][4]

• Nowhere-neat tiling – keine zwei gleich großen Teilquadrate haben eine gesamte Seite gemeinsam.
• No touch tiling – keine zwei gleich großen Teilquadrate haben auch nur den Teil einer Seite gemeinsam.

Es ist evident, dass die No-touch-Varianten eine Teilmenge der Nowhere-neat-Parkettierungen sind.

Beispiele

Abbildung 1 zeigt die perfekte und zugleich einfache Parkettierung geringster Ordnung (21), Abbildung 2 die einfache, unperfekte Quadratur der geringstmöglichen^[5] Ordnung 13 (sie ist zugleich vom Typ no touch tiling, da die jeweils gleich großen Teilquadrate einander nicht berühren), Abbildung 3 eine perfekte, aber zusammengesetzte Quadratur der Ordnung 24 (die grau unterlegten Kacheln oben rechts fügen sich zu einem Rechteck zusammen).

Mrs. Perkins’s Quilt

Mrs. Perkins's Quilt (Lösung)

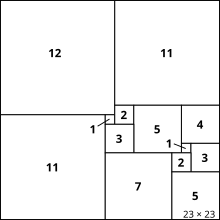
Als „Mrs. Perkins’s Quilt“ wird die Zerlegung eines gegebenen Quadrates in die kleinstmögliche Anzahl von Teilquadraten bezeichnet, ohne dass diese Quadratur perfekt oder einfach zu sein hat. Die Bezeichnung geht zurück auf eine Rätselaufgabe, die der amerikanische Rätselautor Samuel Loyd 1907 und der britische Unterhaltungsmathematiker Ernest Dudeney 1917 publizierten.^[5] In dieser Aufgabe soll ein aus 169 (13 × 13) gleich großen Quadraten zusammengefügter quadratischer Quilt entlang der Nähte in eine möglichst kleine Anzahl von quadratischen Stücken zerschnitten werden. Die Lösung (s. Bild) hat die Ordnung 11; da zwei kongruente Teilstücke (die beiden gelben am oberen Rand) mit einer ganzen Quadratseite aneinandergrenzen, ist sie weder einfach (die beiden Quadrate bilden ein Rechteck) noch perfekt, noch hat sie die Eigenschaften nowhere-neat oder gar no touch.

Geschichte

Sonderbriefmarke von 1998 zum Internationalen Mathematikerkongress in Berlin. Die parkettierte Fläche ist allerdings nur scheinbar ein Quadrat (die Seitenlängen betragen tatsächlich 177 und 176).

Es mag überraschen, dass die Erforschung des eher elementar und einfach anmutenden Problems der Quadratur des Quadrates erst auf das letzte Jahrhundert zurückgeht. Seitdem wurden mehrere Millionen Quadraturen unterschiedlicher Typen und Ordnung entdeckt und dokumentiert, wobei der Ausgangspunkt dieser Entwicklung zunächst die Suche nach der Parkettierung von Rechtecken (nicht zu verwechseln mit der Quadratur des Rechtecks) war.

Beispielhaft seien hier einige Meilensteine dieser Entdeckungsgeschichte genannt.^[3]

• 1903 – Max Dehn beweist, dass ein Rechteck dann und nur dann quadriert werden kann, wenn seine Seiten kommensurabel sind.
• 1936 – Die vier unter dem gemeinsamen Pseudonym „Blanche Descartes“ veröffentlichenden britischen Mathematiker William Thomas Tutte, R. Leonard Brooks, Arthur Harold Stone und Cedric Smith scheitern an dem Beweis ihrer Vermutung, dass Quadrate nicht in eine endliche Anzahl unterschiedlicher Teilquadrate zerlegt werden können. Sie brachten das Problem der Quadratur von Rechtecken und Quadraten mit elektrischen Flüssen in Graphen in Verbindung. 1940 gaben sie ein Beispiel für die Quadratur eines Quadrats mit 69 Quadraten.
• 1939 – Dem deutschen Mathematiker Roland Sprague gelingt die erste Quadratur eines Quadrates, sie ist perfekt und zusammengesetzt, hat die Ordnung 55 und die Seitenlänge 4205.^[6]
• 1939 – R. Leonard Brooks veröffentlicht die erste perfekte und zugleich einfache Quadratur (Ordnung 38, Seitenlänge 4920).
• 1948 – Theophilus Willcocks findet eine Quadratur mit 24 Quadraten.^[7]
• 1978 – A. J. W. Duijvestijn findet mit Computerhilfe die perfekte und einfache Quadratur der Ordnung 21 (Abbildung 1 oben) und beweist, dass dies die Lösung der geringstmöglichen Ordnung und zugleich die einzige dieser Ordnung ist.^[8] (Dass man mindestens 21 benötigt, zeigte er schon 1962.)

Die Quadratur eines Rechtecks erfolgte schon 1925 durch den polnischen Mathematiker Zbigniew Morón. 2008 gelang Frederick und James Henle die lückenlose Zerlegung der Ebene mit Quadraten der Seitenlängen 1,2,3, 4 und so weiter.^[9] 1993 fand S. J. Chapman eine Zerlegung eines Möbiusbandes mit fünf Quadraten unterschiedlicher Größe. Für einen Zylinder benötigt man mindestens neun Quadrate.^[10]

Einzelnachweise

(Quellen siehe Literatur und Weblinks.)

1. ↑ ^{a b} Darling 2004, S. 302
2. ↑ Stewart 1998, S. 10
3. ↑ ^{a b c d} Anderson 2014, Honsberger 2002
4. ↑ Scherer, Devincentis
5. ↑ ^{a b} Anderson 2014
6. ↑ Sprague 1939
7. ↑ Ian Stewart, Professor Stewarts mathematisches Sammelsurium, Rowohlt 2011
8. ↑ Duijvestijn 1978
9. ↑ Henle, Henle, Squaring the plane, American Math. Monthly, Band 115, 2008, S. 3–12
10. ↑ Clifford Pickover, Math Book, Sterling Publ., S. 352

Literatur

• Ian Stewart: Die Quadratur des Quadrates. In: Spektrum der Wissenschaft. Band 4, 1998, ISSN 0170-2971, S. 10 ff. 
• David Darling: The Universal Book of Mathematics. From Abracadabra to Zeno's Paradoxes. Wiley-Blackwell, Hoboken (New Jersey) 2004, ISBN 0-471-27047-4. 
• R. Sprague: Beispiel einer Zerlegung des Quadrats in lauter verschiedene Quadrate. In: Mathematische Zeitschrift. Band 45, 1939, ISSN 0025-5874, S. 607–608.  Online (Digitalisat)
• A. J. W. Duijvestijn: Simple Perfect Squared Square of Lowest Order. In: Journal of Combinatorial Theory, Series B. Band 25, 1978, ISSN 0021-9800, S. 240–243.  Online (Digitalisat)

Weblinks

Commons: Quadratur des Quadrates – Sammlung von Bildern

• Ernest Dudeney: Mrs. Perkins's Quilt, 1917. Faksimile von Aufgabe und Lösung beim Project Gutenberg (englisch)
• Joseph Devincentis: Square the Square. Beispiele für Nowhere-neat- und No-touch-Quadraturen (englisch)
• Stuart Anderson: Squared Squares, 2014. Ausführliche Übersicht mit historischen Informationen (englisch)
• Ross Honsberger: Squaring the Square, University of Waterloo 2002. (englisch)
• Karl Scherer: Square The Square (englisch)