Pyramide (Geometrie)

In der Geometrie ist eine Pyramide ein Polyeder, also ein geometrischer Körper, dessen Kanten die Kanten eines Polygons und außerdem die Verbindungsstrecken der Ecken des Polygons mit der Spitze sind. Das Polygon ist die Grundfläche der Pyramide. Die Spitze der Pyramide liegt nicht in der Ebene der Grundfläche.

Im bekanntesten Fall ist das Polygon ein Quadrat und die Spitze ist ein Punkt senkrecht über dem Mittelpunkt des Quadrats. In diesem Fall entsteht eine gerade quadratische Pyramide. Liegt die Spitze nicht über dem Mittelpunkt des Quadrats, entsteht eine schiefe quadratische Pyramide.

Die Oberfläche der Pyramide, also die Gesamtheit der Seitenflächen einer Pyramide, besteht aus dem gegebenen Polygon, der Grundfläche, und aus Dreiecken mit dem gemeinsamen Punkt ${\displaystyle S}$. Die Dreiecke bilden zusammen die Mantelfläche der Pyramide. Die Kanten des Polygons heißen Grundkanten und die Kanten durch ${\displaystyle S}$ Seitenkanten.

Ist das Polygon regelmäßig, d. h. sind die Kanten gleich lang und liegen die Ecken auf einem Kreis mit Mittelpunkt ${\displaystyle C}$, so heißt die Pyramide regelmäßig. Ist zusätzlich ${\displaystyle C}$ der Lotfußpunkt von ${\displaystyle S}$ auf die Kreisebene, so heißt die Pyramide gerade. Die Dreiecke sind dann alle kongruent und gleichschenklig. Alle anderen Pyramiden heißen schief.^[1]

Hat das Polygon ${\displaystyle n}$ Ecken, den Flächeninhalt ${\displaystyle G}$ und ist die Höhe der Pyramide ${\displaystyle h}$, so gilt:^[2]

Anzahl der Ecken	${\displaystyle n+1}$
Anzahl der Kanten	${\displaystyle 2\cdot n}$
Anzahl der Flächen	${\displaystyle n+1}$
Volumen	${\displaystyle V={\tfrac {1}{3}}\cdot G\cdot h}$
Höhe des Schwerpunkts	${\displaystyle s={\frac {h}{4}}}$
Abbildung für ${\displaystyle n=5}$

Der Schwerpunkt ${\displaystyle C'}$ der Pyramide teilt die Strecke zwischen dem Mittelpunkt der Grundfläche ${\displaystyle C}$ und der Spitze ${\displaystyle S}$ im Verhältnis ${\displaystyle 1:3}$.

Im Fall ${\displaystyle n=3}$ nennt man die Pyramide Tetraeder.

Jede Pyramide ist selbstdual bezüglich der Anordnung der Ecken, Kanten und Flächen.

Es sei ${\displaystyle a}$ die Seitenlänge der quadratischen Grundfläche und ${\displaystyle h}$ die Höhe der Pyramide. Dann hat die gerade quadratische Pyramide folgende geometrische Eigenschaften:

Weitere Eigenschaften enthält der Abschnitt Formeln für gerade regelmäßige Pyramiden.

Eine quadratische Pyramide, deren vier dreieckige Seitenflächen gleichseitig sind, ist der einfachste Johnson-Körper, abgekürzt mit ${\displaystyle J_{1}}$. In diesem Fall gilt ${\displaystyle h={\frac {a}{2}}\cdot {\sqrt {2}}}$ und die Pyramide ist ein halbes reguläres Oktaeder.

Sind für alle geraden quadratischen Pyramiden mit gegebenem Oberflächeninhalt ${\displaystyle A}$ diejenigen mit dem größten Volumen ${\displaystyle V}$ gesucht, dann kann die Seitenlänge ${\displaystyle a}$ und die Höhe ${\displaystyle h}$ in Abhängigkeit von ${\displaystyle A}$ bestimmt werden.

Eine Herleitung für diese Größen geht so:

Man löst die Gleichung ${\displaystyle A=a^{2}+a\cdot {\sqrt {4\cdot h^{2}+a^{2}}}}$ nach ${\displaystyle h^{2}}$ auf, setzt die einzige Lösung für ${\displaystyle h^{2}}$ in die differenzierbare Funktion ${\displaystyle U(a)=9\cdot V^{2}=a^{4}\cdot h^{2}}$ ein und bestimmt das lokale Maximum von ${\displaystyle U}$. Dabei ist der Oberflächeninhalt ${\displaystyle A}$ eine gegebene Konstante und die Seitenlänge ${\displaystyle a}$ ist die Variable der Funktion ${\displaystyle U}$. Beachte, dass ${\displaystyle A}$, ${\displaystyle V}$, ${\displaystyle a}$, ${\displaystyle h}$ positive reelle Zahlen sind.

Wendet man die Kettenregel der Differentialrechnung auf die Funktion ${\displaystyle U(a)=9\cdot (V(a))^{2}}$ an, dann gilt:

${\displaystyle U'(a)=18\cdot V(a)\cdot V'(a)}$

Wegen ${\displaystyle V(a)>0}$ hat die Volumenfunktion ${\displaystyle V}$ genau an den Stellen ${\displaystyle a}$ ein lokales Extremum, wo die Funktion ${\displaystyle U}$ ein lokales Extremum hat. Daraus ergibt sich schließlich folgende einzige Lösung:

${\displaystyle a={\frac {\sqrt {A}}{2}}}$

${\displaystyle h={\sqrt {\frac {A}{2}}}}$

Daraus folgt

${\displaystyle h={\sqrt {2}}\cdot a}$

Bei gegebenem Oberflächeninhalt sind alle Größen der quadratischen Pyramide mit maximalem Volumen eindeutig bestimmt. Für dieses Volumen gilt

${\displaystyle V={\frac {1}{3}}\cdot a^{3}\cdot {\sqrt {2}}={\frac {A\cdot {\sqrt {A}}}{12\cdot {\sqrt {2}}}}={\frac {\sqrt {2}}{24}}\cdot A^{\frac {3}{2}}}$

Die folgende Tabelle enthält Formeln für geometrische Eigenschaften (Größen) einer allgemeinen geraden regelmäßigen Pyramide, einer geraden quadratischen Pyramide und einer geraden regelmäßigen Dreieckspyramide.

Bemerkungen: Für die Herleitung der meisten Formeln werden der Satz des Pythagoras, Sätze für trigonometrischen Funktionen und Sätze für den Arkustangens verwendet.

Der Raumwinkel in den Ecken der Grundfläche, wo drei Seitenflächen (ein regelmäßiges ${\displaystyle n}$-Eck und zwei gleichschenklige Dreiecke) mit den Innenwinkeln ${\displaystyle \alpha }$, ${\displaystyle \alpha _{1}}$, ${\displaystyle \alpha _{1}}$ zusammentreffen, wird mit dem Satz von L’Huilier berechnet (siehe Raumwinkel - Kanten-Formel).^[3]

Der Raumwinkel in der Spitze, wo ${\displaystyle n}$ Seitenflächen zusammentreffen, kann auch mit dem Satz von L’Huilier berechnet werden, indem die regelmäßige Pyramide in ${\displaystyle n}$ nicht regelmäßige Tetraeder mit den Kantenlängen ${\displaystyle a}$, ${\displaystyle l}$, ${\displaystyle l}$, ${\displaystyle h}$, ${\displaystyle R_{u}}$, ${\displaystyle R_{u}}$ zerlegt wird, wobei ${\displaystyle R_{u}={\tfrac {a}{2\cdot \sin \left({\frac {\pi }{n}}\right)}}}$ der Umkreisradius der regelmäßigen Grundfläche ist. Dabei wird der Raumwinkel in der Spitze wegen Rotationssymmetrie in ${\displaystyle n}$ gleich große und kongruente Teilwinkel zerlegt. Also haben diese ${\displaystyle n}$ nicht regelmäßige Tetraeder dort eine gemeinsame Ecke. In dieser Ecke treffen jeweils drei Seitenflächen mit den Innenwinkeln ${\displaystyle \alpha _{3}}$, ${\displaystyle \gamma _{2}}$, ${\displaystyle \gamma _{2}}$ zusammen.

Eine andere Möglichkeit, den Raumwinkel in der Spitze zu berechnen, ist, die Formel von H. C. Rajpoot für den rotationssymmetrischen Ecken-Raumwinkel anzuwenden.^[4] Dabei müssen die Innenwinkel aller ${\displaystyle n}$ Seitenflächen, die in einer Ecke zusammentreffen, gleich groß sein, was für alle regelmäßigen Pyramiden der Fall ist.

Für bestimmte Werte von ${\displaystyle n}$ und ${\displaystyle h}$ ergeben sich Zusammenhänge mit platonischen Körpern:

• Für ${\displaystyle n=3}$ und ${\displaystyle h={\frac {a}{3}}\cdot {\sqrt {6}}}$ ergibt sich das regelmäßige Tetraeder.
• Für ${\displaystyle n=4}$ und ${\displaystyle h={\frac {a}{2}}\cdot {\sqrt {2}}}$ ergibt sich eine quadratische Pyramide, die ein halbes reguläres Oktaeder ist.
• Für ${\displaystyle n=5}$ und ${\displaystyle h={\frac {a}{10}}\cdot {\sqrt {50-10\cdot {\sqrt {5}}}}}$ ergibt sich eine regelmäßige fünfseitige Pyramide, die ein Teil des Ikosaeders ist.

Mit einer analogen Herleitung wie für eine gerade quadratische Pyramide (siehe oben) kann man beweisen:

Unter allen geraden regelmäßigen Pyramiden mit einem regelmäßigen ${\displaystyle n}$-Eck als Grundfläche mit gegebenem Oberflächeninhalt ${\displaystyle A}$ hat diejenige das größte Volumen, für die gilt:

${\displaystyle a=\left({\frac {A\cdot \tan \left({\frac {\pi }{n}}\right)}{n}}\right)^{\frac {1}{2}}}$

${\displaystyle h=\left({\frac {2\cdot A\cdot \cot \left({\frac {\pi }{n}}\right)}{n}}\right)^{\frac {1}{2}}={\sqrt {\frac {2\cdot A}{\pi }}}\cdot {\sqrt {{\frac {\pi }{n}}\cdot \cot \left({\frac {\pi }{n}}\right)}}}$

Daraus folgt

${\displaystyle h={\sqrt {2}}\cdot \cot \left({\frac {\pi }{n}}\right)\cdot a}$

Für den Beweis kann man die Gleichung ${\displaystyle A={\frac {n\cdot a}{4}}\cdot \left(a\cdot \cot \left({\frac {\pi }{n}}\right)+{\sqrt {4\cdot h^{2}+a^{2}\cdot \cot ^{2}\left({\frac {\pi }{n}}\right)}}\right)}$ nach ${\displaystyle h^{2}}$ auflösen, die einzige Lösung für ${\displaystyle h^{2}}$ in die differenzierbare Funktion ${\displaystyle U(a)=144\cdot n^{2}\cdot \tan ^{2}\left({\frac {\pi }{n}}\right)\cdot V^{2}=a^{4}\cdot h^{2}}$ einsetzen und bestimmt das lokale Maximum von ${\displaystyle U}$.

Bemerkungen: Ist stattdessen unter allen geraden regelmäßigen Pyramiden mit gegebenem Volumen ${\displaystyle V}$ diejenige mit dem kleinsten Oberflächeninhalt gesucht, dann ergibt sich als Lösung im Wesentlichen dieselbe Pyramide. Von allen geraden regelmäßigen Pyramiden hat diese die größte Sphärizität.

Der Umkreisradius der regelmäßigen Grundfläche ist

${\displaystyle r_{u}={\frac {a}{2\cdot \sin \left({\frac {\pi }{n}}\right)}}={\sqrt {\frac {A}{4\cdot \pi }}}\cdot {\sqrt {\frac {\frac {2\cdot \pi }{n}}{\sin \left({\frac {2\cdot \pi }{n}}\right)}}}}$

Das maximale Volumen ist ${\displaystyle V=\left({\frac {A^{3}\cdot \cot \left({\frac {\pi }{n}}\right)}{72\cdot n}}\right)^{\frac {1}{2}}={\frac {A\cdot {\sqrt {A}}}{6\cdot {\sqrt {2\cdot \pi }}}}\cdot {\sqrt {{\frac {\pi }{n}}\cdot \cot \left({\frac {\pi }{n}}\right)}}}$.

Für ${\displaystyle n}$ gegen unendlich konvergiert ${\displaystyle a}$ monoton fallend gegen ${\displaystyle 0}$ und ${\displaystyle h}$ konvergiert monoton steigend gegen ${\displaystyle h_{\text{Kegel}}={\sqrt {\tfrac {2{\dot {A}}}{\pi }}}}$.

Dies ist die Höhe eines Kegels mit maximalem Volumen bei gegebener Oberflächeninhalt ${\displaystyle A}$. Bei der Herleitung wird der Grenzwert ${\displaystyle \lim _{x\to 0}{\frac {\sin(x)}{x}}=1}$ verwendet.
Der Radius des Basiskreises des Kegels ist ${\displaystyle r_{\text{Kegel}}={\sqrt {\frac {A}{4\cdot \pi }}}}$, seine Höhe ${\displaystyle h_{\text{Kegel}}=2\cdot {\sqrt {2}}\cdot r_{\text{Kegel}}={\sqrt {\frac {2\cdot A}{\pi }}}}$ und sein Volumen ${\displaystyle V_{\text{Kegel}}={\frac {A\cdot {\sqrt {A}}}{6\cdot {\sqrt {2\cdot \pi }}}}}$.

Für den Quotienten der Volumen gilt

${\displaystyle {\frac {V}{V_{\text{Kegel}}}}={\sqrt {{\frac {\pi }{n}}\cdot \cot \left({\frac {\pi }{n}}\right)}}}$

Dieser Quotient konvergiert gegen 1.

Regelmäßige Pyramiden, die ein regelmäßiges Vieleck als Grundfläche haben, können verwendet werden, um einen Kreiskegel zu approximieren, der nach Definition einen Kreis als Grundfläche hat.

Wenn die Grundfläche ein regelmäßiges ${\displaystyle n}$-Eck ist, kann formal der Grenzwert für unendlich großes ${\displaystyle n}$ gebildet werden. Der Kreiskegel kann sozusagen als regelmäßige Pyramide aufgefasst werden, wobei die Grundfläche unendlich viele Ecken und die Seitenlänge des ${\displaystyle n}$-Ecks den Grenzwert 0 hat.

Im Folgenden soll auf diese Weise das Volumen des Kreiskegels hergeleitet werden.

Mithilfe der Formel für den Flächeninhalt eines regelmäßigen ${\displaystyle n}$-Ecks (siehe Regelmäßiges Polygon – Umfang und Flächeninhalt) ergibt sich für das Volumen ${\displaystyle V}$ der regelmäßigen Pyramide, wenn der Umkreisradius ${\displaystyle r_{u}}$ des ${\displaystyle n}$-Ecks bekannt ist:

${\displaystyle V={\frac {1}{3}}\cdot G\cdot h={\frac {1}{3}}\cdot {\frac {n\cdot r_{u}^{2}}{2}}\cdot \sin \left({\frac {2\cdot \pi }{n}}\right)\cdot h={\frac {n\cdot r_{u}^{2}\cdot h}{6}}\cdot \sin \left({\frac {2\cdot \pi }{n}}\right)}$

Um das Volumen des Kreiskegels zu bestimmen, kann der Grenzwert für ${\displaystyle n}$ gegen unendlich gebildet werden. Dieser Grenzwert ergibt sich mit Hilfe der Formel ${\displaystyle \lim _{x\to 0}{\frac {\sin(x)}{x}}=1}$:

${\displaystyle V_{\text{Kreiskegel}}=\lim _{n\to \infty }{\frac {n\cdot r_{u}^{2}\cdot h}{6}}\cdot \sin \left({\frac {2\cdot \pi }{n}}\right)={\frac {n\cdot r_{u}^{2}\cdot h}{6}}\cdot {\frac {2\cdot \pi }{n}}\cdot \lim _{n\to \infty }{\frac {\sin \left({\frac {2\cdot \pi }{n}}\right)}{\frac {2\cdot \pi }{n}}}={\frac {2\cdot \pi \cdot n\cdot r_{u}^{2}\cdot h}{6\cdot n}}\cdot 1={\frac {\pi \cdot r_{u}^{2}\cdot h}{3}}}$

Für die Berechnung des Volumens einer allgemeinen Pyramide gibt es mehrere Möglichkeiten.

Für eine von den Vektoren ${\displaystyle {\vec {a}},{\vec {b}},{\vec {c}}}$ aufgespannte dreiseitige Pyramide (allgemeines Tetraeder) kann das Volumen mit Hilfe des Spatprodukts berechnet werden:

${\displaystyle V={\frac {1}{6}}\cdot \left|\left({\vec {a}}\times {\vec {b}}\right)\cdot {\vec {c}}\right|}$

Jedes beliebige Vieleck kann in Dreiecke zerlegt werden, deren Ecken mit den Ecken des Vielecks übereinstimmen. Daher kann jede allgemeine Pyramide in allgemeine Tetraeder zerlegt werden. Wenn die Koordinaten aller Ecken bekannt sind, sind auch alle entsprechenden Vektoren bekannt und das Volumen der allgemeinen Pyramide kann als Summe der Volumen dieser allgemeinen Tetraeder berechnet werden.

Die Volumenformel

${\displaystyle V={\frac {1}{3}}\cdot G\cdot h}$

lässt sich elementargeometrisch in zwei Schritten beweisen:

• Ein Würfel kann in drei kongruente Pyramiden mit quadratischer Grundfläche zerlegt werden, deren Spitzen mit derselben Ecke des Würfels übereinstimmen. Die Grundfläche dieser drei gleichen Pyramiden sind die drei Seitenflächen des Würfels, die diese Ecke nicht enthalten.
• Zwei Pyramiden mit gleicher Höhe, deren Grundflächen denselben Flächeninhalt haben, haben dasselbe Volumen. Zum Beweis dieser Aussage kann man das Prinzip von Cavalieri und die Gesetze der zentrischen Streckung heranziehen.

Das Volumen einer allgemeinen Pyramide mit der Grundfläche ${\displaystyle G}$ und der Höhe ${\displaystyle h}$ kann berechnet werden, wenn man sich vorstellt, dass die die Pyramide aus beliebig dünnen Schichten besteht, die parallel zur Grundfläche sind.

Die ${\displaystyle y}$-Achse sei so definiert, dass sie durch die Spitze der Pyramide verläuft und orthogonal zur Grundfläche ist. Dann ist die Höhe der Pyramide Teil der ${\displaystyle y}$-Achse. Bezeichnet man den Flächeninhalt der Schicht im Abstand ${\displaystyle y}$ von der Spitze mit ${\displaystyle A(y)}$, dann ist ${\displaystyle A}$ eine reelle Funktion mit der Variablen ${\displaystyle y}$. Aus den Eigenschaften der zentrischen Streckung kann man eine Formel für ${\displaystyle A(y)}$ herleiten:

${\displaystyle {\frac {A(y)}{G}}={\frac {y^{2}}{h^{2}}}}$

${\displaystyle A(y)={\frac {G}{h^{2}}}\cdot y^{2}}$

Daraus ergibt sich das Volumen der Pyramide als Integral der Funktion ${\displaystyle A(y)}$ auf dem Intervall ${\displaystyle [0,h]}$ nach dem Prinzip von Cavalieri:

${\displaystyle V=\int _{0}^{h}A(y)\ \mathrm {d} y=\int _{0}^{h}{\frac {G}{h^{2}}}\cdot y^{2}\ \mathrm {d} y={\frac {G}{h^{2}}}\cdot \int _{0}^{h}y^{2}\ \mathrm {d} y={\frac {G}{h^{2}}}\cdot \left[{\frac {1}{3}}\cdot y^{3}\right]_{0}^{h}={\frac {G}{h^{2}}}\cdot \left({\frac {1}{3}}\cdot h^{3}-{\frac {1}{3}}\cdot 0^{3}\right)={\frac {1}{3}}\cdot G\cdot h}$

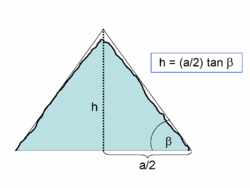
Bei einer großen Pyramide lassen sich die Kantenlängen der Basis direkt gut vermessen, jedoch nicht die Höhe, die nicht direkt zugänglich ist. Im Folgenden sollen die grundsätzlichen Schwierigkeiten dargelegt werden, die nicht so sehr mit der Methodik des Messverfahrens selbst zusammenhängen. Ein einfaches geometrisches Verfahren zur Höhenbestimmung größerer Objekte ist die Betrachtung aus der Entfernung und die Bestimmung des Sehwinkels (in vereinfachter Form durch die nebenstehende Grafik aufgezeigt).

Im Abstand ${\displaystyle s}$ von der unteren Pyramidenkante wird die Spitze der Pyramide unter dem gemessenen Winkel ${\displaystyle \alpha }$ angepeilt. Der Abstand des Beobachtungspunktes von der Pyramidenspitze in horizontaler Linie ist somit der um die halbe Grundseite vermehrte Abstand von der Pyramidenkante ${\displaystyle a/2+s.}$ Die Höhe ${\displaystyle h}$ ergibt sich aus der Formel in der Grafik. Damit wäre die Bestimmung der Höhe kein großes Problem. Es gibt jedoch folgende Schwierigkeiten:

• Die Spitze der Pyramide liegt nicht unbedingt exakt über dem Mittelpunkt der Grundfläche.
• Die Länge der Basiskante der Pyramide ist nicht sauber bestimmbar (abgebrochene Steine, Erosion).
• Die Spitze ist nicht mehr vorhanden (abgetragen).
• Der Neigungswinkel der Pyramide ist schwer bestimmbar (Abtragung, Erosion).

Das entspricht bei den bekannten großen Pyramiden weitgehend der Realität. Es muss definiert werden, von welchem Bodenniveau aus die Höhe der Pyramide gelten soll, also wo ihre Basis angenommen wird; von dieser aus muss die Höhenabweichung des Beobachtungspunktes, an dem ${\displaystyle \alpha }$ gemessen wird, genau berücksichtigt werden. Die Winkelmessung selbst kann in der Regel sehr präzise ausgeführt werden. Angenommen, die Basislänge ${\displaystyle a}$ der Pyramide ließe sich nicht genauer als auf 30 cm und damit die Entfernung ${\displaystyle a/2+s}$ zum Messpunkt nicht genauer als auf 15 cm bestimmen. Dadurch würde bei einem Sehwinkel ${\displaystyle \alpha }$ von angenommenen 35° die Höhe um den Betrag von etwa 10 cm ungenau sein. Außerdem soll noch der Neigungswinkel ${\displaystyle \beta }$ der Seitenfläche bestimmt werden. Eine hypothetische große Pyramide der Basislänge von 200 m und einer Höhe von 140 m hätte bei einer Ungenauigkeit der Höhenangabe von 10 cm eine Ungenauigkeit der Neigungswinkelangabe von etwa einer Bogenminute (54°27′44″ bei ${\displaystyle h=140{,}0\,\mathrm {m} }$ gegenüber 54°26′34″ mit ${\displaystyle h=139{,}9\,\mathrm {m} }$). Das gilt nun für Pyramiden, deren Spitze noch vorhanden ist. Die Realität sieht aber anders aus. Die Höhenbestimmung gibt also nicht die ursprüngliche Höhe wieder, sondern die Höhe der abgetragenen Pyramide.

Die Spitze muss also extrapoliert werden. Das nebenstehende Bild zeigt schematisch das Problem. Sowohl die Seitenflächen als auch die Spitze sind durch Abriss und Verwitterung deutlich abgetragen:

Die Höhe ${\displaystyle h}$ wäre daher gemäß der Formel aus der direkten Bestimmung des Neigungswinkels ${\displaystyle \beta }$ zugänglich. Wie ersichtlich, ist die Bestimmung mit großen Fehlern behaftet. Eine Ausnahme bildet die Chephren-Pyramide, weil diese im oberen Teil noch die originalen Decksteine hat. Der Winkel ${\displaystyle \beta }$ ist dadurch genauer bestimmbar als bei den anderen Pyramiden. Das erklärt die gute Übereinstimmung verschiedener Autoren hinsichtlich des Neigungswinkels.

Damit wird klar, dass bei realen Pyramiden weder die Höhe auf den Zentimeter noch der Neigungswinkel auf die Bogensekunde exakt angegeben werden kann.

Verwandte Formen in der Geometrie sind der Pyramidenstumpf (eine parallel zur Grundfläche „abgeschnittene“ Pyramide) und die Doppelpyramide (ein Polyeder aus zwei spiegelsymmetrischen Pyramiden mit derselben Grundfläche).

Eine Hyperpyramide ist eine Verallgemeinerung auf ${\displaystyle n}$ Dimensionen. Die in diesem Artikel beschriebene Pyramide ist eine dreidimensionale Hyperpyramide. Eine zweidimensionale Hyperpyramide wäre ein Dreieck, eine vierdimensionale ein Pentachoron.

Mit der Pyramide in der Architektur befasst sich der Artikel Pyramide (Bauwerk).

• Tetraeder
• Pyramidenstumpf
• Doppelpyramide
• Hyperpyramide
• Kegel

Commons: Pyramids (geometry) – Sammlung von Bildern, Videos und Audiodateien

• Eric W. Weisstein: Pyramid. In: MathWorld (englisch).

1. ↑ Kleine Enzyklopädie Mathematik. 2. völlig überarbeitete Auflage, Harri Deutsch, Thun (CH) / Frankfurt 1977, ISBN 3-87144-323-9, S. 208.
2. ↑ Hans-Joachim Bartsch: Mathematische Formeln. 5., unveränderter Nachdruck der 11. Auflage, Buch- und Zeit-Verlagsgesellschaft, Köln 1977, S. 152.
3. ↑ Wolfram MathWorld: Spherical Excess
4. ↑ Harish Chandra Rajpoot: Solid angles subtended by the platonic solids (regular polyhedra) at their vertices. In: SlideShare. März 2015, abgerufen am 21. September 2025.