Produktregel
Die Produktregel oder Leibnizregel (nach Gottfried Wilhelm Leibniz) ist eine grundlegende Regel der Differentialrechnung. Mit ihr wird die Ableitung eines Produktes von Funktionen aus den Ableitungen der einzelnen Funktionen berechnet. In Lagrange-Notation lautet die Produktregel
Der Vorteil dieser Regel liegt darin, dass es im Allgemeinen einfacher ist, die Ableitungen beider Faktoren separat zu berechnen, als jene des gesamten Produkts auf einmal.
Zum Beispiel kann mit der Produktregel die Ableitung der Funktion schnell berechnet werden, wenn die Ableitungen der Faktoren und schon bekannt sind, die sich als sowie berechnen lassen mithilfe der Ableitungsregeln elementarer Funktionen. Für den Fall, dass eine der beiden Funktionen konstant ist, geht die Produktregel in die einfachere Faktorregel über.
Neben ihrer Bedeutung für explizite Berechnungen hat die Produktregel auch theoretische Konsequenzen. Der hinter ihr stehende mathematische Satz besagt, dass Differenzierbarkeit, also die Eigenschaft von Funktionen, eine Ableitungsfunktion zu haben, stabil unter Produktbildung ist. Wenn also Funktionen und (in einem Punkt) differenzierbar sind, dann auch ihr Produkt .
Das Analogon hinsichtlich Addition ist die Summenregel und das Analogon hinsichtlich der Division ist die Quotientenregel.
Im Rahmen der Integralrechnung kann die Produktregel dazu verwendet werden, die partielle Integration herzuleiten. Ähnlich wie die Integration gemäß dem Fundamentalsatz der Analysis als Umkehroperator der Differentiation gesehen werden kann, entspricht die partielle Integration dem Umkehroperator der Produktregel.
Einführende Erklärung
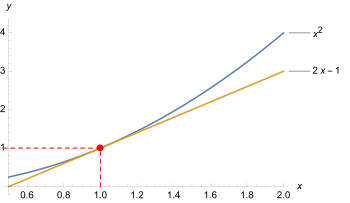
Ist eine Funktion in einem Punkt differenzierbar, so ist es möglich, sie in diesem Bereich relativ gut durch eine lineare Funktion anzunähern. Der Vorteil daran ist, dass man Begriffe wie Steigung, also das Maß, um wie viel Einheiten sich ein Vorgang ändert, wenn man den Eingabewert verändert, für lineare Funktionen verstanden hat. Indes ist es zu Beginn nicht klar, wie zum Beispiel die Steigung einer Funktion wie im Punkt zu begreifen ist. Durch die Annäherung mittels einer linearen Funktion, quasi als gedankliche Hilfestellung, kann man aber den Begriff der Steigung auch auf Kurven, also nicht-lineare Vorgänge, ausweiten. Die Steigung am Punkt einer Kurve entspricht dann per Definition der Steigung der linearen Funktion, welche die Kurve dort am besten annähert, aber die Steigung einer linearen Funktion ist wegen der Gradlinigkeit des Schaubildes gut verstanden. Auf diese Weise können auch komplizierten, nicht-linearen Vorgängen lokale Veränderungsraten zugeordnet werden. Dieser Vorgang entspricht dem Kerngedanken der Differentialrechnung.
Der Gedanke hinter der Produktregel fußt nun wiederum auf einem einfachen Mechanismus. Sind zum Beispiel die Funktionen und separat im Punkt im Sinne der Differentialrechnung gut verstanden, können sie durch lineare Funktionen
- und für fast gleich 0
angenähert werden. Dabei haben die Näherungen, wie man aus der Erfahrung mit linearen Funktionen weiß, die Steigungen bzw. . Das Prinzip der Differentialrechnung ordnet also den „schwierigen Kurven“ von und im Punkt ebenfalls die Steigungen und zu. In kurzer Schreibweise:
- bzw.
Die Näherungen und sind so gewählt, dass sie im Punkt selbst perfekt sind (Tangentenprinzip), es herrscht dann im Grenzfall sogar Gleichheit: bzw. , also kurz
- bzw.
Es ist nun naheliegend, dass sich ihr Produkt über das Produkt dieser Näherungen wieder annähert. Zum Beispiel sind, zunächst einzeln betrachtet, die Zahlen und gute Näherungen für die Zahlen und , also ist deren Produkt eine Näherung für kurz
Nehmen nun und gedanklich den Platz von und , sowie und von und in der oberen Anschauung ein, gilt diesem Gedanken folgend
- und
Durch Ausmultiplizieren von und anschließendes termweises Zusammenfassen erhält man daraus
Der Term ist für verschwindend gering. Daher kann er bei der linearen Näherung des Produktes ignoriert werden:
Auf der rechten Seite steht nun wieder eine lineare Näherung. Die Steigung von im Punkt ist also
Exakt dieselbe Überlegung gilt für beliebige feste Punkte , wenn man oben durch in den Näherungstermen ersetzt. Die analytische Gestalt der Produktregel ist also das Resultat des mittleren Termes von in ausmultiplizierter Form.
Aussage der Produktregel
Sind die Funktionen und von einem Intervall in die Menge der reellen oder der komplexen Zahlen an einer Stelle differenzierbar, so ist auch die durch
- für alle
definierte Funktion an der Stelle differenzierbar, und es gilt[1]
oder kurz:
Letztere Schreibweise ist besonders dann in Gebrauch, wenn und , also damit auch , im gesamten Definitionsbereich differenzierbar sind.
Geschichte

Als Entdecker der Produktregel wird in der Literatur häufig Gottfried Wilhelm Leibniz genannt, der sie in seiner bahnbrechenden Nova Methodus pro Maximis et Minimis (1684), dem ersten Werk über das Kalkül der Infinitesimalrechnung, zusammen mit Summen- und Quotientenregel publizierte.[2][3] Allerdings hatte Leibniz bereits im November 1675 in einem Manuskript mit dem Titel Pro methodo tangentium inversa et aliis tetragonisticis specimina et inventa die Regel
formuliert und diese „einen äußerst bemerkenswerten und für alle Kurven geltenden Satz“ bezeichnet.[4] Hierbei nutzte er seine eigens eingeführte Notation für infinitesimale Größen. In einer weiteren Arbeit vom 11. Juli 1677 lieferte Leibniz schließlich erste Beweise für sowohl die Produkt- als auch die Quotientenregel. Um zu zeigen, schreibt Leibniz
und argumentiert, dass die Größe „unendlich viel kleiner“ sei verglichen zum Rest, womit nur noch überbleibt.[5] Auch war Leibniz im Jahr 1710 im Stande, eine allgemeine Form der Produktregel zu formulieren. Diese bezieht sich auf höhere Ableitungen eines Produktes, also zweite, dritte, vierte usw. Ableitung. Leibniz schrieb:[6]
- etc.,
- etc.,
wobei er die Notationen für die -te Potenz und für das -te Differential verwendete. Leibniz erkannte, dass die allgemeine Produktregel in direkter Verbindung zum binomischen Lehrsatz stand und sich diese durch die Analogie zwischen dimensionsgebundener Homogenität (im Sinne gleicher Potenzen in Polynomen) und Potenzen unendlich kleiner Größen ausdrückt.[7] In einer Leibniz-Übersetzung im Jahr 1920 behauptete J. M. Child jedoch, dass Isaac Barrow die Produktregel, wie auch andere Techniken, zuvor entwickelt habe. Dort heißt es:
„Newton, with his great knowledge of and inclination toward geometrical reasoning, backed with his personal intercourse with Barrow, could appreciate the finality of Barrow’s proofs of the differentiation of a product, quotient, power, root, logarithm and exponential, and the trigonometrical functions, in a way that Leibniz could not.“
„Newton, mit seiner großen Kenntnis und Neigung zu geometrischem Denken, unterstützt durch seinen persönlichen Verkehr mit Barrow, konnte die Bedeutung von Barrows Beweisen für die Differenzierung eines Produkts, eines Quotienten, einer Potenz, einer Wurzel, eines Logarithmus und eines Exponentials sowie der trigonometrischen Funktionen in einer Weise schätzen, wie es Leibniz nicht konnte.“
Bereits im Jahr 1916 hatte Child eine englische Übersetzung von Teilen der Lectiones Geometricae von Barrow veröffentlicht,[9] in deren Vorwort er Barrow zum eigentlichen und einzigen Erfinder der Differential- und Integralrechnung erhoben hatte. Damit ging Child nach Einschätzung von Thomas Sonar jedoch zu weit, denn man könne aus Barrows geometrischen Konstruktionen den Hauptsatz zwar herauslesen, allerdings hätte Child dies aus der Position des heutigen, mathematisch gebildeten Menschen getan. Barrow wäre es laut Sonar hingegen versagt geblieben, diese tiefe Einsicht aus seinen eigenen Arbeiten zu gewinnen.[10]
Anwendungsbeispiele
Im Folgenden sei stets
- Ist und so ist und man erhält aus der Kenntnis von und mit der Produktregel
- Ist und , so ist und wegen und folgt daraus
- Ist und , so ist und wegen und folgt daraus
- Verwendet man die Kurznotation so erhält man beispielsweise für die Ableitung folgender Funktion
- Ausmultipliziert ergibt sich
Erklärung und Beweis


Das Produkt zweier reeller an einer Stelle differenzierbarer Funktionen und hat an der Stelle den Wert der als Flächeninhalt eines Rechtecks mit den Seiten und gedeutet werden kann. Ändert sich nun um so ändert sich um und um Die Änderung des Flächeninhalts setzt sich dann (siehe Abbildung) zusammen aus
Dividiert man durch so ergibt sich mit
der Differenzenquotient der Produkt- oder Flächeninhaltsfunktion an der Stelle .
Für gegen 0 konvergiert und damit der ganze letzte Summand gegen 0, sodass man an der Stelle
erhält, wie behauptet. Dies ist auch im Wesentlichen die Argumentation, wie sie sich in einem ersten Beweis der Produktregel 1677 in einem Manuskript von Gottfried Wilhelm Leibniz findet. Die Produktregel, die er dort gemeinsam mit der Quotientenregel beweist, war damit eine der ersten Regeln zur Anwendung der Infinitesimalrechnung, die er herleitete. Er benutzte allerdings keinen Grenzwert, sondern noch Differentiale und schloss, dass wegfällt, weil es im Vergleich zu den anderen Summanden infinitesimal klein sei. Leonhard Euler benutzte noch dasselbe Argument, erst bei Augustin-Louis Cauchy findet sich ein Beweis mit Grenzwerten, der den heutigen Maßstäben an mathematische Strenge genügt:
Beweis
Gegeben sei die Funktion durch Die Ableitung von an einer Stelle ist dann durch den Grenzwert des Differenzenquotienten
gegeben. Addition und Subtraktion des Terms liefert
Das Ausführen der beiden Grenzübergänge liefert die Produktregel
Verallgemeinerungen
Bei allen Betrachtungen und Verallgemeinerungen der Produktregel ist darauf zu achten, dass die Faktoren beziehungsweise alle Faktoren an der betrachteten Stelle differenzierbar sind. Ansonsten kann die Ableitung des Produkts an der Stelle eine Definitionslücke haben.
Mehrfache Differentiation
Auch die Regel für Ableitungen der Ordnung (höhere Ableitungen) für ein Produkt aus zwei Funktionen war schon Gottfried Wilhelm Leibniz bekannt und wird entsprechend manchmal ebenfalls als Leibnizregel bezeichnet. Sie ergibt sich aus der Produktregel mithilfe vollständiger Induktion:[11][12]
Das Symbol ist das Summenzeichen für reelle Zahlen. Die hier auftretenden Ausdrücke der Form sind Binomialkoeffizienten. Die obige Formel enthält die eigentliche Produktregel als Spezialfall und impliziert, dass der -Vektorraum der -mal differenzierbaren Funktionen auf sogar eine -Algebra ist. Einfach gesprochen folgt also, dass wenn und jeweils -mal differenzierbar sind, dies auch auf ihr Produkt zutrifft.
Bemerkung: Diese Verallgemeinerung für die mehrfache Differentiation eines Produkts aus zwei Funktionen hat auffallende Ähnlichkeit zum binomischen Lehrsatz
Diese Ähnlichkeit ist kein Zufall. Der übliche Induktionsbeweis läuft in beiden Fällen vollkommen analog. Man kann die Leibnizregel aber auch mit dem binomischen Lehrsatz beweisen.
Produkte von endlich vielen differenzierbaren Funktionen
Wird die erste Ableitung eines Produkts von endlich vielen differenzierbaren Funktionen betrachtet, dann gilt folgende allgemeinere Gleichung
wobei das Produktzeichen für reelle Zahlen ist. Haben die Funktionen keine Nullstellen, so kann man diese Regel auch in der übersichtlichen Form
schreiben. Derartige Brüche bezeichnet man als logarithmische Ableitungen. Hintergrund dabei ist die Gleichung.
Für die mehrfache Differentiation von mehr als zwei Faktoren lässt sich ganz entsprechend das Multinomialtheorem verwenden. Es gilt
mit den Multinomialkoeffizienten .
Die Anzahl der Summanden, die dabei insgesamt addiert werden, also die Anzahl der Lösungen der Gleichung für natürliche Zahlen ist , siehe Kombination mit Wiederholung.
Komplexe Differenzierbarkeit
Die Produktregel gilt auch für komplex differenzierbare Funktionen. Ist eine offene Teilmenge der komplexen Zahlen und komplex differenzierbare Funktionen in , dann ist ebenfalls komplex differenzierbar in und es gilt
Insbesondere gilt: Sind und holomorph in , so folgt in ganz und die Funktion ist erneut holomorph in .
Produkte von Skalaren, Vektoren und Matrix-Vektor-Produkte
Beim Beweis der Produktregel werden aus den Werten von Linearkombinationen (Summen, Differenzen, Produkte mit Zahlen) gebildet, ebenso aus den Werten von Die Rollen von und sind dabei klar getrennt: ist der linke Faktor, der rechte. Der Beweis überträgt sich deswegen auf alle Produktbildungen, die sowohl im linken als auch im rechten Faktor linear sind. Insbesondere gilt die Produktregel auch für
- das Produkt von Skalar und Vektor (Skalarmultiplikation):
- das Skalarprodukt von zwei Vektoren:
- das Vektorprodukt (Kreuzprodukt) von zwei Vektoren:
Vektoren bzw. Matrizen sind dabei als Funktionen einer unabhängigen Variablen zu verstehen.
Höherdimensionaler Definitionsbereich
Verallgemeinert man auf Funktionen mit höherdimensionalem Definitionsbereich, so lässt sich die Produktregel wie folgt formulieren: Es seien eine offene Teilmenge, differenzierbare Funktionen und ein Richtungsvektor. Dann gilt die Produktregel für die Richtungsableitung:[15]
Entsprechend gilt für die Gradienten
In der Sprache der differenzierbaren Mannigfaltigkeiten lauten diese beiden Aussagen:
- Sind ein Tangentialvektor und lokal differenzierbare Funktionen, dann gilt
- Sind lokal differenzierbare Funktionen, so gilt die folgende Beziehung zwischen den äußeren Ableitungen:
Höhere partielle Ableitungen
Sei , und . Dann gilt:[16]
Allgemeine differenzierbare Abbildungen
Es seien ein offenes Intervall, eine Banachalgebra (z. B. die Algebra der reellen oder komplexen -Matrizen) und differenzierbare Funktionen. Dann gilt:
Dabei bezeichnet der Operator die Multiplikation in der Banachalgebra.
Sind allgemeiner und Banachräume, und differenzierbare Funktionen, so gilt ebenfalls eine Produktregel, wobei die Funktion des Produktes von einer Bilinearform übernommen wird. Von dieser wird verlangt, dass sie stetig ist, also beschränkt:
- für alle
mit einer festen Konstante . Dann gilt die Produktregel
Entsprechende Aussagen gelten für höherdimensionale Definitionsbereiche.
Leibniz-Regel für dividierte Differenzen
Die Leibnizregel lässt sich auf dividierte Differenzen übertragen:[17]
Der Spezialfall
- mit und schließt die originale Leibnizregel mit ein.
Derivationen
Allgemein nennt man Abbildungen welche die Produktregel
erfüllen, Derivationen. Die Reihenfolge der Faktoren ist hier für den Fall einer Derivation mit einer Algebra und einem -Linksmodul gewählt.
Im Zusammenhang mit - oder -graduierten Algebren („Superalgebren“) muss der Begriff der Derivation jedoch durch den der Antiderivation ersetzt werden. Die entsprechende Gleichung lautet dann
für homogene Elemente Dabei bezeichnet den Grad von Das prominenteste Beispiel einer Antiderivation ist die äußere Ableitung für Differentialformen
Siehe auch
Literatur
Die Produktregel für Funktionen wird in jedem Buch erläutert, das Differentialrechnung in allgemeiner Form behandelt.
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. 7. Auflage. Vieweg, Braunschweig 2004, ISBN 3-528-67224-2.
- Otto Forster: Analysis 2. Differentialrechnung im Rn. Gewöhnliche Differentialgleichungen. 6. Auflage. Vieweg, Braunschweig 2005, ISBN 3-528-47231-6.
- Konrad Königsberger: Analysis. 2 Bde. Springer, Berlin 2004, ISBN 3-540-41282-4.
- Charles Henry Edwards Jr.: The Historical Development of the Calculus. Springer, New York 1979, ISBN 0-387-90436-0.
Weblinks
- Herleitung der Produktregel und zahlreiche Beispiele ( vom 29. Februar 2008 im Internet Archive)
Einzelnachweise
- ↑ Herbert Amann, Joachim Escher: Analysis 1, Dritte Auflage, Birkhäuser, S. 321.
- ↑ Gottfried Wilhelm Leibniz: Nova Methodus pro Maximis et Minimis. In: Acta Eruditorum. Band 3, 1684, S. 467 (archive.org).
- ↑ John Stillwell: Mathematics and Its History, Springer, S. 171.
- ↑ J. M. Child: The Early Mathematical Manuscripts Of Leibniz, S. 107.
- ↑ Charles Henry Edwards: The Historical Development of the Calculus, Springer, S. 255–256.
- ↑ Gottfried Wilhelm Leibniz: Mathematische Schriften V, S. 379–380.
- ↑ H. J. M. Bos: Differentials, Higher-Order Differentials and the Derivative in the Leibnizian Calculus, Arch. Hist. Exact Sci. 14, 1975, S. 33.
- ↑ J. M. Child: The Early Mathematical Manuscripts Of Leibniz, S. 28–29, Fußnote 58.
- ↑ J. M. Child: Geometrical Lectures of Isaac Barrow. Chicago, London, 1916.
- ↑ Thomas Sonar: 3000 Jahre Analysis, Springer, S. 330.
- ↑ Alexander Grigoryan: Analysis II. Universität Bielefeld, S. 43, abgerufen am 3. November 2025.
- ↑ Herbert Amann, Joachim Escher: Analysis 1, Dritte Auflage, Birkhäuser, S. 325.
- ↑ Ilja Nikolajewitsch Bronstein: Taschenbuch der Mathematik. 5. Auflage. Verlag Harri Deutsch, 2001, ISBN 3-8171-2005-2, S. 661.
- ↑ Josiah Willard Gibbs: Vector Analysis. A Text-book for the Use of Students of Mathematics and Physics. Charles Scribner's Sons, New York City 1901, S. 118 (archive.org).
- ↑ Herbert Amann, Joachim Escher: Analysis 2, Zweite Auflage, Birkhäuser, S. 175.
- ↑ Lawrence C. Evans: Partial Differential Equations. ISBN 0-8218-0772-2, 19. Auflage, S. 12.
- ↑ De Boor: Divided Differences. Surveys in Approximation Theory. Band 1, 2005, S. 46–69.
Auf dieser Seite verwendete Medien
Autor/Urheber: ThibautLienart, Lizenz: CC BY-SA 3.0
Illustration for the graphical proof of the product rule.
Autor/Urheber: Googolplexian1221, Lizenz: CC BY-SA 4.0
The function f(x) = x^2 is linearized by g(x) = 2x-1.
Autor/Urheber: Der ursprünglich hochladende Benutzer war Honina in der Wikipedia auf Deutsch, Lizenz: CC BY-SA 3.0
Veranschaulichung der Produktregel



