Problem der Museumswächter
Das Problem der Museumswächter (englisch Art gallery problem) ist eine Fragestellung der algorithmischen Geometrie. Dabei wird folgende Situation untersucht:
„Gegeben sei eine polygonale Fläche mit Rand , interpretiert als Grundriss eines Museums. Wähle nun möglichst wenige Punkte (‚Wächter‘) im Innern des Polygons, sodass jeder Punkt im Innern des Polygons durch eine Gerade, die ganz in einschließlich Rand liegt, mit einem Wächter verbunden werden kann.“
Das ist äquivalent dazu, ein Polygon minimal sternförmig zu überdecken.
In der Praxis tritt das Problem in der Robotik auf, wenn „künstliche Intelligenzen“ Bewegungsmuster in Abhängigkeit von ihren Umgebungen ausführen sollen.[1] Manche Fragestellungen der digitalen Bildbearbeitung lassen sich auf Wächterprobleme zurückführen.[2] Auch Beleuchtungsprobleme einer Bühne und das Problem bei der Beobachtung von Tierpopulationen in großen Gebieten können als Wächterproblem modelliert werden. Eine weitere Anwendung ist die Aufstellung der Infrastruktur für die Wetterbeobachtung oder zur Warnung vor Naturkatastrophen.
Das Problem fällt komplexitätstheoretisch in die Klasse der APX-Probleme, das heißt, dass wahrscheinlich[A 1] kein Algorithmus existiert, der es für allgemeine Polygone effizient und korrekt löst. Andererseits hat man für das Problem und seine Varianten obere Schranken für die Zahl der Wächter gefunden und beweisen können, dass diese auch scharf sind. Das heißt, sie können nicht weiter verbessert werden, ohne dass man sich auf spezielle Polygonklassen einschränkt.
Die wahrscheinlich erste systematische Betrachtung von Sichtbarkeitsfragen regte Victor Klee im August 1973 auf einer Konferenz in Stanford an, indem er das Museumsproblem für Punktwächter und eine sich als korrekt herausgestellte Vermutung formulierte.[3] Zwei Jahre später präsentierte Chvátal eine bewiesene Lösung des Problems.[4]
Elementare Beispiele
Wir betrachten zunächst die „einfache“ Version des Problems mit stationären Wächtern. Man überlege sich für eine vorgegebene kleine Kantenzahl ein Polygon, das möglichst viele Wächter benötigt. Bei einem Dreieck und einem Viereck hat man wenig Möglichkeiten, weil offensichtlich stets ein Wächter ausreicht. Bei einem Fünfeck ist das weiterhin richtig, wobei diese Einsicht nicht mehr ganz so offensichtlich ist:
- Spezialfall 5-seitiger Polygone
Abbildung 1
Abbildung 2
Abbildung 3
Abbildung 4
Die ersten drei Abbildungen zeigen Stereotype aller möglichen Fünfecke: Jedes Fünfeck kann entweder keine, eine oder zwei konkave Ecken besitzen, also Ecken die einen Innenwinkel von mehr als 180° beziehungsweise im Bogenmaß haben. Das folgt aus der Tatsache, dass in jedem -Eck die Summe der Innenwinkel gleich ist, im Fall ist diese Summe . Sie lässt also höchstens zwei konkave Ecken zu.
Für das 4. Beispiel bräuchte man zwei Wächter: einen auf einem der Berührungspunkte der Dreiecke und einen weiteren im jeweils verbleibenden Dreieck. Allerdings würde man dort monieren, dass das Polygon „eigentlich“ neun Seiten hat, wenn man Überschneidungen verbieten möchte. Für gewöhnlich tut man das auch. Von nun an werden nur noch solche schneidungsfreien Polygone betrachtet.
- Weitere „kritische Graphen“ für kleine Kantenzahlen
Abbildung 5
Abbildung 6
Abbildung 7
Abbildung 8
Im Fall (Abbildungen 5 und 6) tritt der Fall ein, dass Polygone existieren, die nicht von einem Wächter allein bewacht werden können, allerdings reichen stets zwei Wächter aus. Führt man solche Überlegungen weiter fort, kann man beobachten, dass nach jeweils drei weiteren Kanten ein weiterer Wächter nötig werden kann. Ein Polygon, das zu einer Kantenzahl eine maximale Wächterzahl benötigt, nennt man in dem Zusammenhang des Problems ein kritisches Polygon.
Satz von Chvátal
Der Beweis dafür, dass die oberen Beispiele tatsächlich kritische Polygone sind, also dass für neun- beziehungsweise zwölfkantige Polygone stets drei respektive vier Wächter ausreichen, ist ein Spezialfall folgenden Satzes:
„Zur Bewachung eines jeden überschneidungsfreien, geschlossenen und planaren Polygons mit Seiten sind [A 2] Wächterpunkte stets ausreichend und manchmal notwendig.“
Als Beweis gibt es im Wesentlichen zwei Versionen: Eine geometrische Variante, wie sie Chvátal zunächst angab, und eine graphentheoretische, die von S. Fisk angegeben wurde.[5] Fisks Beweis benutzt einige wohlbekannte Resultate aus der Graphentheorie, sodass der Beweis vergleichsweise kurz ist und als etwas ästhetischer gilt. Andererseits lässt er im Gegensatz zu Chvátal einige Verallgemeinerungen nicht zu.
Beweis
- (Nach Fisk) Zu einem geschlossenen planaren und überschneidungsfreien Polygon lassen sich geeignete Sehnen zwischen seinen Ecken ziehen, sodass das Polygon in, bis auf die Sehnen, paarweise disjunkte Dreiecke zerfällt. So eine Zerlegung heißt naheliegenderweise Triangulation und ihre Existenz ist unter den gegebenen Voraussetzungen allgemein bewiesen. Weiterhin ist bekannt, dass sich die Ecken eines triangulierten Polygons unter Verwendung von nur drei Farben so färben lassen, dass benachbarte Ecken verschiedene Farben haben.[6] Jede Farbklasse ist dann offensichtlich eine gültige Wächtermenge; Insbesondere ist das für die kleinste Farbklasse wahr, die gerade Ecken enthält.
Bereits vor dem Beweis dieses Satzes war bekannt, dass diese obere Schranke, falls sie sich als gültig herausstellen sollte, nicht weiter verschärft werden könnte. Dazu betrachtet man folgende Folge von Graphen mit Kanten. Jedes solche Polygon benötigt Wächter.

Anlehnend an Fisks Konstruktionsbeweis entwickelten Avis und Toussaint einen Algorithmus, der eine Wächtermenge der Größe konstruiert.[7] Seine Laufzeit hängt im Wesentlichen davon ab, wie effizient eine Triangulation gefunden werden kann. Einige einfache Methoden realisieren das in quadratischer Zeit. In ihrem Artikel schlagen sie eine Version in vor.[A 3] 1990 hat Chazelle einen Algorithmus mit Laufzeit vorgestellt.
Die Färbung ist dann relativ leicht konstruierbar, wenn man annimmt, dass die Triangulation eine Datenstruktur übergibt, die alle Adjazenzinformationen enthält. Im Allgemeinen kann das nicht gesichert werden. Die Leistung von Toussaint und Avis war es, eine Färbung in Linearzeit zu finden, allein unter der Benutzung einer Liste von Sehnenkanten der Triangulation.
Veranschaulichung des Beweises
Zur Veranschaulichung des Beweises wird das unten stehende Polygon betrachtet. Der erste Schritt besteht darin, das Polygon zu triangulieren (siehe Abbildung 1). Dann wendet man eine -Färbung an (Abbildung 2) und stellt fest, dass es rote, blaue und grüne Scheitelpunkte gibt. Die Farbe mit den wenigsten Scheitelpunkten ist blau oder rot, so dass das Polygon durch Wächter abgedeckt werden kann (Abbildung 3). Dies stimmt mit dem Satz von Chvátal überein, da das Polygon Scheitelpunkte hat und .
Abbildung 1
Abbildung 2
Abbildung 3
Varianten und Verallgemeinerungen
Im Satz von Chvátal wird angenommen, dass die Wächter auf den Eckpunkten stehen. Die angegebene obere Schranke bleibt jedoch gültig, wenn die Beschränkung auf Wächter an den Ecken gelockert wird, um Wächter an jedem Punkt zuzulassen, der nicht außerhalb des Polygons liegt. Darüber hinaus wurden eine Reihe weiterer Verallgemeinerungen und Spezifikationen des ursprünglichen Satz von Chvátal untersucht.
Orthogonale Polygone
Ein wesentlicher Spezialfall des Wächterproblems ist die Einschränkung auf orthogonale Polygone.[A 4] Darunter versteht man Polygone, die ausschließlich die Innenwinkel und , das sind 90° beziehungsweise 270°, annehmen. Solche Polygone betrachtet man in geometrischen Anwendungen, die stark an das kartesische Koordinatensystem gebunden sind: darunter fallen Designprobleme hochintegrierter Schaltungen, Architektur und einige Algorithmen auf Rastergraphiken.[8]
Die zunächst naheliegende Vermutung, dass man mit dieser Einschränkung eine bessere Schranke an die Zahl der nötigen Wächter würde beweisen können, wurde 1980 durch einen Satz von Klawe und Kleitman bestätigt.[9] Sie zeigten die Existenz so genannter „konvexer Quadrilaterationen“:[A 5] Das sind, analog zur Triangulation, Zerlegungen eines Polygons in konvexe Vierecke, indem Sehnen zwischen gewissen Ecken gezogen werden, die ganz im Polygon liegen. Ihr Beweis dazu ist sehr allgemein gehalten hält auch für eine entsprechende Aussage über Polygonen mit (endlich vielen) „Löchern“ oder „Überlappungen“.[A 6] Es lässt sich vergleichsweise leicht zeigen, dass der Dualgraph einer konvexen Quadrilateration keinen der Kuratowskiminoren, also die Graphen und , enthalten kann. Nach dem Satz von Kuratowski ist der Graph dann planar und nach dem Vierfarbentheorem vierfärbbar. Daraus folgt der Satz:
„Zur Bewachung eines jeden überschneidungs- und lochfreien sowie planaren und orthogonalen Polygons mit Seiten sind Wächterpunkte stets ausreichend und manchmal notwendig.“
Dass Wächter manchmal notwendig sind, zeigt in Analogie zum Beispiel des allgemeinen Falls der „orthogonale Kamm“:

Um die Existenz der konvexen Quadrilaterationen zu zeigen, nutzt der Beweis folgende aufeinander aufbauende Konzepte:
Eine „rechte“ und eine „linke“ Kante und eines Polygons heißen benachbart, falls
- Das Innere von „links“ von und rechts von liegt.
- und „sehen“ einander (Das heißt, es existieren Punkte und , sodass die Verbindung ganz in enthalten ist.)
- Der Abstand zwischen und zueinander ist unter den Bedingungen (1) und (2) minimal.
Daraus folgt sofort, dass zu einer Kante keine Nachbarin existieren muss, falls aber eine existiert so kann o. B. d. A. davon ausgegangen werden, dass diese eindeutig ist.[A 7] Sind zwei benachbarte Kanten durch eine vertikale Kante miteinander verbunden, nennt man die drei Kanten zusammen ein Ohr. Für „obere“ und „untere“ Kanten definiert man die Nachbarschafts- und Ohreigenschaft ganz analog.
In gegebenen Polygonen solche Ohren zu finden, ist deshalb interessant, weil man relativ leicht beweisen kann, dass jede konvexe Quadrilateration jedes Ohr enthalten muss. Allerdings muss man, um die Aussage des Wächtertheorems zu erhalten, das Konzept etwas allgemeiner fassen, denn nicht jedes Polygon muss ein Ohr enthalten.
Außerdem gibt es solche (Ohrenthaltenden) Polygone, die es gestatten, ein Polygon durch Abspaltung eines konvexen Vierecks auf ein oder mehrere kleinere, das heißt mit wenigstens einem Loch oder einer Kante weniger, zurückzuführen, und solche, die so eine Reduktion nicht gestatten. Diese nennt man reduzibel respektive irreduzibel. Klawe und Kleitmann konnten zeigen, dass orthogonale Polygone
- entweder in diesem Sinne reduzibel sind
- oder ein Ohrenpaar (zwei Ohren, sodass die Verbindungskanten der benachbarten Kanten einander sehen) enthalten,
- oder zwei benachbarte Kanten enthalten, die kein Ohr bilden,
- oder unendlich viele Ecken haben müssen.
Für den Fall des Ohrenpaars und der benachbarten Kanten konnten sie auch eine Reduktion auf ein kleineres Polygon angeben und so induktiv die Existenz der vorgeschlagenen Quadrilaterationen für endliche Polygone begründen.
- Beispiele zu konvexen Quadrilaterationen
Konvexe Quadrilaterationen von orthogonalen Polygonen sind im Allgemeinen nicht eindeutig. Dieses Polygon hat kein Ohr.
Das Viereck ist ein Ohr. ist kein Ohr, weil mit benachbart ist. Die in diesem Fall eindeutige konvexe Quadrilateration (eingezeichnet) kann nicht aus einer allgemeinen Triangulation konstruiert werden. (könnte das Dreieck enthalten)
Algorithmen
Einen Versuch der Umsetzung des eben vorgestellten Beweises stellt Sack in seiner Promotionsschrift von 1984 vor.[10]
Einen anderen Beweisansatz und einen daraus abgeleiteten Algorithmus hat Lubiw 1985 entwickelt.[11]
Festungsproblem
Derick Wood und Joseph Malkelvitch stellten in den 1970ern unabhängig voneinander die Frage nach zwei Verallgemeinerungen des Problems der Museumswächter: Anstelle Punkte zu finden, die das Innere eines Polygons bewachen, fragten sie nach Punkten, die das Äußere bewachen oder beides leisten. Wood prägte dafür die Namen Festungsproblem (für Bewachungsprobleme von äußeren Gebieten) und Problem des Gefängnishofs (für Probleme bei denen beides bewacht werden soll). Das Festungsproblem ist insofern zufriedenstellend gelöst, als dass scharfe Aussagen zur benötigten Wächterzahl für ein Polygon in der Eckenzahl bewiesen werden konnten.

„Zur Lösung des Festungsproblems sind Eckenwächter manchmal notwendig und immer ausreichend“
Ein Beispiel für die Notwendigkeit ist jedes konvexe Polygon. Dass das hinreicht, folgt aus folgender Konstruktion: Zu einem allgemeinen Polygon betrachte die konvexe Hülle. Trianguliere nun den Teil der Ebene, der innerhalb der konvexen Hülle, jedoch außerhalb des Polygons liegt. Wähle einen künstlichen Knoten und verbinde alle Punkte der konvexen Hülle mit ihm. An einem beliebigen Knoten der konvexen Hülle wird das Polygon nun „geöffnet“: wird ersetzt durch Knoten und mit bis auf je eine Kante, die sie mit ihrem Nachbarn auf der konvexen Hülle verbinden, identischen Inzidenzen wie . Der resultierende Graph mit Knoten ist ein Triangulationsgraph, also dreifärbbar. Man rechnet dann elementar aus, dass eine minimale chromatische Klasse, die nicht enthält, höchstens von der Ordnung ist. Die Übertragung des Beweises auf den orthogonalen Fall hat Aggarwal durchgeführt und er kommt darin zu dem Ergebnis, dass Eckenwächter stets ausreichend und manchmal notwendig sind. Beide Beweise liefern Linearzeitalgorithmen zur Konstruktion einer entsprechenden Wächtermenge.

Wenn man die Beschränkung aufhebt, dass Wächter ausschließlich an den Ecken platziert werden dürfen, kann man zeigen, dass dafür stets ausreichend und manchmal nötig sind. Zum Beweis hat sich eine Idee von Shermer als einsichtig erwiesen. Man konstruiert einen Triangulationsgraphen: Zwei zusätzliche Punkte werden rechts und links des Polygons hinreichend weit entfernt gewählt. Mit der konvexen Hülle kann dann ein Graph mit Knoten erklärt werden, zu dem eine Triangulation existiert. In dem Fall, dass die Knotenzahl auf der konvexen Hülle gerade ist, ist dieser Graph dann 3-färbbar, die Zusatzknoten bekommen die Farbe Eins, die Punkte auf der Hülle dann alternierend Zwei und Drei. Ist sie ungerade, kann man mit einem Trick[12] einen weiteren Knoten hinzunehmen und ist im geraden Fall. Eine kleinste chromatische Klasse enthält dann Knoten.
Resultate der Wächtertheorie im Überblick
(Quelle: O’Rourke[13])
| gesichteter Bereich | Polygonstruktur | Löcher | Wächtertyp | untere Schranke | obere Schranke | Diskussion |
|---|---|---|---|---|---|---|
| Innen | allgemein | Ecken | Satz von Chvátal | |||
| Untere Schranke, obere Schranke fast trivial[14] | ||||||
| Untere Schranke für kleine . Obere in O’Rourke S. 125 ff. | ||||||
| Kanten | ||||||
| sternförmig | Ecken | Einige untere Schranken hier. Obere Schranken und Rest in O’Rourke S. 116 ff. | ||||
| Linie | ||||||
| Diagonale | ||||||
| Kanten | ||||||
| orthogonal | Ecken | Orthogonale Polygone | ||||
| Analog zum allgemeinen Fall mit Löchern O’Rourke S. 140 ff. | ||||||
| Punkt | ||||||
| Ecken | ||||||
| Diagonal | O’Rourke S. 108 ff. Nach Aggarwal. | |||||
| Außen | allgemein | Ecken | Festungsproblem | |||
| Punkt | ||||||
| orthogonal | Ecken | Festungsproblem | ||||
| Innen und außen | allgemein | Ecken | Füredi-Keitmann | |||
| konvex | Füredi-Keitmann | |||||
| orthogonal | Hoffmann-Kriegel | |||||
| ||||||
Weitere kritische Beispiele
- Für sternförmige Polygone
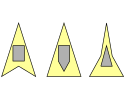
Beweisidee der unteren Schranke in der Eckenzahl für sternförmige Polygone: Für Ecken braucht man hier 8 Eckenwächter. (Einen für jeden „Zacken“. Keine Ecke bewacht 2 Zacken oder mehr.)
Beweis der unteren Schranke in der Zahl de konkaven Ecken für sternförmige Polygone: Für je zwei Zacken braucht man einen Wächter an deren konkaven Ecken. Keine Ecke mehr als zwei Zacken.
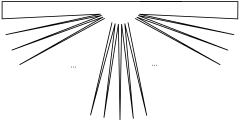
Beweisidee der unteren Schranke in der Eckenzahl für Sternförmige Polygone: Für braucht man hier 5 Kantenwächter. Bei der Verallgemeinerung für größere n muss man die Zacken Derart spitz wählen, dass die durch jeden Zacken induzierten Strahlen für jeden Zacken eine andere Kante des „Kreises“ schneiden.
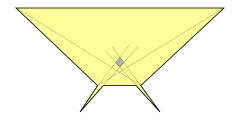
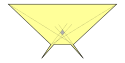
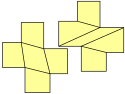
Beispiel eines sternförmigen Polygons, das zwei Diagonalenwächter benötigt. Zwei der vier möglichen Diagonalen sind eingezeichnet: Keine schneidet die grau hervorgehobene Kernregion. Dieses Beispiel wurde von Shermer und Suri entdeckt.
- Schranke in der Zahl konkaver Ecken und Polygone mit Löchern.
Es gibt Polygonklassen, die für jede konkave Ecke einen Wächter benötigen.
Für Ecken werden 3 Wächter benötigt. Das linke Polygon geht auf Julian Sidarto zurück. Die beiden Rechten auf Tomas Shermer.
Hier braucht man 4 Wächter für Ecken. Das Linke geht auf Shermer zurück; das Rechte auf Arthur Delcher. Diese und die vorherigen Beispiele mit Löchern wurden in einer Hausaufgabe eines Seminars von O’Rourke gefunden.
und drei Löcher brauchen 9 Eckenwächter.
Literatur
- J. Urrutia: Art gallery and illumination problems. In: Handbook of computational geometry. 2000, S. 973–1027.
- A. Aggarwal: The art gallery theorem: its variations, applications and algorithmic aspects. 1984.
- J. O’Rourke: Art gallery theorems and algorithms. Oxford University Press Oxford, 1987 (smith.edu [PDF]).
- Frank Hoffmann, Klaus Kriegel: Algorithms and Computation. 1993, A graph coloring result and its consequences for some guarding problems, S. 78–87, doi:10.1007/3-540-57568-5_237.
- Zoltán Füredi, D. J. Kleitman: The prison yard problem. In: Combinatorica. Band 14, Nr. 3, 1994, S. 287–300, doi:10.1007/BF01212977.
Anmerkungen
- ↑ Bewiesen wurde die Zugehörigkeit unter der Voraussetzung . Viele Mathematiker gehen davon aus, der Beweis hat sich in den jüngeren Jahrzehnten jedoch als genuin schwierig herausgestellt. (Siehe P-NP-Problem)
- ↑ Die Symbole sind die Gaußklammern. Sie runden den eingeschlossenen Ausdruck ab. Beispiel:
- ↑ Zur -Notation siehe Landau-Symbol
- ↑ Andere gebrauchte Bezeichnungen dafür sind rektilinear, isothetisch und rektanguloid.
- ↑ O’Rourke gebraucht den Begriff Quadrilateralization.
- ↑ Um Überlappungen zu Modellieren untersucht man Polygone als orthogonale, geschlossene Jordan-Kurven auf einer Riemannschen Fläche.
- ↑ Man kann zu jedem orthogonalen Polygon ein „beliebig nahes“ Polygon mit zu identischer Quadrilateration finden, dessen Ecken paarweise verschiedene Koordinaten haben.
Einzelnachweise
- ↑ N. J. Nilsson: A mobile automaton: An application of artificial intelligence techniques. Storming Media, 1969.
- ↑ L. S. Davis, M. L. Benedikt: Computational models of space: Isovists and isovist fields. 1979.
- ↑ R. Honsberger: Mathematical Gems II: The Dolciani Mathematical Expositions. In: Mathematical Association of America. Band 84, 1976.
- ↑ a b V. Chvatal: A combinatorial theorem in plane geometry. In: J. Combin. Theory Ser. B. Band 18, Nr. 39–41, 1975, S. 32.
- ↑ S. Fisk: A short proof of Chvátals watchman theorem. In: J. Combin. Theory Ser. B. Band 24, Nr. 3, 1978, S. 374.
- ↑ Für die Existenzbeweise von Triangulationen und der Färbung kann man O’Rourke (1987) studieren
- ↑ D. Avis, G. T. Toussaint: An efficient algorithm for decomposing a polygon into star-shaped polygons. In: Pattern Recognition. Band 13, Nr. 6, 1981, S. 395–398 (Online [PDF]).
- ↑ O’Rourke: S. 31
- ↑ J. Kahn, M. Klawe, D. Kleitman: Traditional galleries require fewer watchmen. In: SIAM Journal on Algebraic and Discrete Methods. Band 4, 1983, S. 194, doi:10.1137/0604020.
- ↑ Jörg-Rüdiger Wolfgang Sack: Rectilinear computational geometry. ACM, 1984, abgerufen am 11. März 2010. und J. R. Sack, G. Toussaint: A linear-time algorithm for decomposing rectilinear star-shaped polygons into convex quadrilaterals. In: Proceedings 19th Conference on Communications, Control, and Computing. 1981, S. 21–30.
- ↑ Anna Lubiw: Decomposing polygonal regions into convex quadrilaterals. In: Proceedings of the first annual symposium on Computational geometry. ACM, Baltimore, Maryland, United States 1985, ISBN 0-89791-163-6, S. 97–106, doi:10.1145/323233.323247 (online [abgerufen am 13. März 2010]).
- ↑ vgl. O’Rourke S. 152 ff.
- ↑ O’Rourke: S. 267
- ↑ B. M Chazelle: Computational geometry and convexity. New Haven Yale Univ. 1980.
Auf dieser Seite verwendete Medien
Autor/Urheber: Kimdc98, Lizenz: CC BY-SA 4.0
Figure representing the least color of a 3-coloring of a polygon.
Autor/Urheber: Kimdc98, Lizenz: CC BY-SA 4.0
Figure representing a 3-coloring of the vertices of a polygon
Autor/Urheber: Kimdc98, Lizenz: CC BY-SA 4.0
Figure representing a triangulation of a polygon