Portal:Mathematik/Lesenswerte Artikel

Übersicht

Qualitätssicherung

Projekt

Exzellente Artikel

Lesenswerte Artikel

Portal:Mathematik

Allgemein

• Portalseite
• Diskussionsseite

Mitarbeit

• Qualitätssicherung
• Arbeitslisten
• Exzellenzinitiative
• Fehlende Artikel
• Artikel ohne Quellenangaben
• Verwaiste Artikel

Projekt

• Hinweise zur Mitarbeit
• Projektinterna
• Portalchat
• Ansprechpartner
• Artikelcharts
• Kategorienbaum Mathematik
• Quellen im Web

Siehe auch

• Literaturstipendium
• Hilfe zu TeX

Commons: Mathematik

Beweisarchiv

Algorithmensammlung

Lesenswerte Artikel zu mathematischen Themen

A*-Algorithmus

Der A*-Algorithmus gehört zur Klasse der informierten Suchalgorithmen. Er dient in der Informatik der Berechnung eines kürzesten Pfades zwischen zwei Knoten in einem Graphen mit positiven Kantengewichten. Er wurde das erste Mal 1968 von Peter Hart, Nils J. Nilsson und Bertram Raphael beschrieben. Der Algorithmus gilt als Verallgemeinerung und Erweiterung des Dijkstra-Algorithmus, in vielen Fällen kann aber umgekehrt A* auch auf Dijkstra reduziert werden. ↪ zum Artikel

AVL-Baum

Der AVL-Baum ist eine Datenstruktur in der Informatik, und zwar ein binärer Suchbaum mit der zusätzlichen Eigenschaft, dass sich an jedem Knoten die Höhe der beiden Teilbäume um höchstens eins unterscheidet. Diese Eigenschaft lässt seine Höhe nur logarithmisch mit der Zahl der Schlüssel wachsen und macht ihn zu einem balancierten binären Suchbaum. Die maximale (und mittlere) Anzahl der Schritte (Vergleiche), die nötig sind, um An- oder Abwesenheit eines Schlüssels festzustellen, hängt direkt mit der Höhe zusammen. Ferner ist der maximale Aufwand für Operationen zum Einfügen und Entfernen eines Schlüssels proportional zur Höhe des Baums und damit ebenfalls logarithmisch in der Zahl der Schlüssel; der mittlere Aufwand ist sogar konstant, wenn das Positionieren auf das Zielelement nicht mitgerechnet wird. ↪ zum Artikel

B-Baum

(c) Flying sheep, CC-BY-SA-3.0

Ein B-Baum ist in der Informatik eine Daten- oder Indexstruktur, die häufig in Datenbanken und Dateisystemen eingesetzt wird. Ein B-Baum ist ein immer vollständig balancierter Baum, der Daten sortiert nach Schlüsseln speichert. Er kann binär sein, ist aber im allgemeinen kein Binärbaum. Das Einfügen, Suchen und Löschen von Daten in B-Bäumen ist in amortisiert logarithmischer Zeit möglich. B-Bäume wachsen – und schrumpfen – anders als viele Suchbäume von den Blättern hin zur Wurzel. ↪ zum Artikel

Begriffsschrift

Die Begriffsschrift ist ein schmales, weniger als hundert Seiten umfassendes Buch des Jenaer Mathematikers und Philosophen Gottlob Frege zur Logik. Es wurde 1879 mit dem Untertitel „Eine der arithmetischen nachgebildete Formelsprache des reinen Denkens“ veröffentlicht und gilt allgemein als die wichtigste Veröffentlichung im Bereich der Logik seit Aristoteles' Organon.

Frege gelang in diesem Buch zum ersten Mal eine Formalisierung der klassischen Prädikatenlogik, und damit die erste Formalisierung einer Logik, in der sich ein hinreichend großer Teil der Mathematik, aber auch der natürlichen Sprache ausdrücken ließ. Gemeinsam mit George Booles Mathematical Analysis of Logic von 1847 markiert die Begriffsschrift deshalb den Beginn der modernen formalen Logik. Die Bezeichnung Begriffsschrift wird auch für den von Frege definierten logischen Kalkül sowie für Freges logische Notation verwendet. Frege entwarf die Begriffsschrift zur Unterstützung seiner Forschung an den Grundlagen der Mathematik. ↪ zum Artikel

Benfordsches Gesetz

Das Benfordsche Gesetz, auch Newcomb-Benford's Law (NBL), zählt zu den universellen Verteilungsgesetzen der Stochastik. Es beschreibt eine fundamentale Gesetzmäßigkeit der Verteilung der Ziffernstrukturen der Zahlen in Datensätzen, zum Beispiel ihrer ersten Ziffern, seien es Datensätze über Einwohnerzahlen von Städten oder über Geldbeträge in der Buchhaltung, von Naturkonstanten oder Datensätze wissenschaftlicher Beobachtungen.

1881 wurde diese Gesetzmäßigkeit von dem Mathematiker Simon Newcomb entdeckt und im „American Journal of Mathematics“ publiziert. Er soll bemerkt haben, dass in den benutzten Büchern mit Logarithmentafeln die Seiten mit Tabellen mit Eins als erster Ziffer deutlich schmutziger waren als die anderen Seiten, weil sie offenbar öfter benutzt worden seien. Die Abhandlung Newcombs blieb unbeachtet und war schon in Vergessenheit geraten, als der Physiker Frank Benford (1883–1948) diese Gesetzmäßigkeit wiederentdeckte und darüber 1938 neu publizierte. ↪ zum Artikel

Braess-Paradoxon

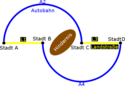
Das Braess-Paradoxon (nach dem Mathematiker Dietrich Braess) ist eine Veranschaulichung der Tatsache, dass eine zusätzliche Handlungsalternative unter der Annahme rationaler Einzelentscheidungen zu einer Verschlechterung der Situation für alle führen kann.

Braess originale Arbeit zeigt eine paradoxe Situation, in der der Bau einer zusätzlichen Straße (also einer Kapazitätserhöhung) dazu führt, dass sich bei gleich bleibendem Verkehrsaufkommen die Fahrtdauer für alle Autofahrer erhöht, d. h. die Kapazität des Netzwerkes reduziert wird. ↪ zum Artikel

Brinkmanship

Brinkmanship (engl.: „Spiel mit dem Feuer“ oder „Politik am Rande des Abgrunds“) bezeichnet in der Spieltheorie eine risikoreiche Strategie bei Verhandlungen. Der Spieler geht mit dem Gegenspieler zur Klärung einer Streitfrage sinnbildlich bis an den Rand (engl. “brink”) einer Felsklippe, wodurch der Gegenspieler zum Nachgeben gebracht werden soll, bevor am Ende beide in den Abgrund fallen. Die Brinkmanship wird beispielsweise in der Außenpolitik von Staaten oder bei Streiks von Arbeitnehmern angewendet. ↪ zum Artikel

Chaosforschung

Die Chaosforschung ist ein Teilgebiet der Mathematik und Physik und befasst sich im Wesentlichen mit Systemen, deren Dynamik unter bestimmten Bedingungen empfindlich von den Anfangsbedingungen abhängt, so dass ihr Verhalten nicht langfristig vorhersagbar ist. Da diese Dynamik einerseits den physikalischen Gesetzen unterliegt, andererseits aber irregulär erscheint, bezeichnet man sie als deterministisches Chaos. Chaotische Systeme sind nichtlineare dynamische Systeme. Beispiele sind der Schmetterlingseffekt beim Wetter, Turbulenzen, Wirtschaftskreisläufe, bestimmte Musterbildungsprozesse, wie beispielsweise Erosion, sowie neuronale Netze und damit letztlich auch menschliches Verhalten. ↪ zum Artikel

Damenproblem

Das Damenproblem ist eine schachmathematische Aufgabe. Es sollen jeweils acht Damen auf einem Schachbrett so aufgestellt werden, dass keine zwei Damen einander nach den Schachregeln schlagen können. Die Figurenfarbe wird dabei ignoriert, und es wird angenommen, dass jede Figur jede andere angreifen könnte. Anders ausgedrückt, es sollen sich keine zwei Damen die gleiche Reihe, Linie oder Diagonale teilen. Im Mittelpunkt steht die Frage nach der Anzahl der möglichen Lösungen.

Das Problem kann auf Schachbretter beliebiger Größe verallgemeinert werden. Dann gilt es, n nicht-dominierende Damen auf einem Brett von n x n Feldern zu positionieren. Für n = 8 hat das Damenproblem 92 verschiedene Lösungen. Betrachtet man Lösungen als gleich, die sich durch Spiegelung oder Drehung des Brettes aus einander ergeben, verbleiben noch zwölf Lösungen. ↪ zum Artikel

Direkte Numerische Simulation

Unter Direkter Numerischer Simulation, kurz DNS, versteht man die rechnerische Lösung der vollständigen instationären Navier-Stokes-Gleichungen. Sie unterscheidet sich von anderen Berechnungsmethoden der Strömungsmechanik dadurch, dass kleinskalige turbulente Schwankungen aufgelöst und nicht durch Turbulenzmodelle dargestellt werden.

Aufgrund der zeitlich variierenden, räumlich kleinen Schwankungen in einer turbulenten Strömung ist neben der hohen räumlichen Auflösung eine instationäre Betrachtungsweise für die detaillierte Beschreibung der physikalischen Vorgänge erforderlich. Die DNS ist damit die genaueste Methode, Strömungen zu berechnen; sie stellt allerdings auch die höchsten Anforderungen an das numerische Verfahren sowie an die zur Verfügung stehende Rechenleistung. Deshalb findet die DNS hauptsächlich in der Grundlagenforschung Verwendung. ↪ zum Artikel

Fundamentalsatz der Analysis

Der Fundamentalsatz der Analysis, auch bekannt als Hauptsatz der Differential- und Integralrechnung, bringt die beiden grundlegenden Konzepte der Analysis, nämlich das der Integration und das der Differentiation, miteinander in Verbindung. Genauer sagt er aus, dass Ableiten und Integrieren jeweils die Umkehrung des anderen sind. Der Satz besteht aus zwei Teilen, die manchmal als erster und zweiter Hauptsatz der Analysis bezeichnet werden. Die konkrete Formulierung des Satzes und sein Beweis variieren je nach Aufbau der betrachteten Integrationstheorie. Hier wird zunächst das Riemann-Integral betrachtet. ↪ zum Artikel

Gaußsches Eliminationsverfahren

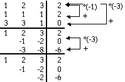
Das Gauß'sche Eliminationsverfahren oder einfach Gauß-Verfahren (nach Carl Friedrich Gauß) ist ein Algorithmus aus den mathematischen Teilgebieten der linearen Algebra und der Numerik. Es ist ein wichtiges Verfahren zum Lösen von linearen Gleichungssystemen und beruht darauf, dass elementare Umformungen zwar das Gleichungssystem ändern, aber die Lösung erhalten. Dies erlaubt es, jedes Gleichungssystem auf Stufenform zu bringen, an der die Lösung durch sukzessive Elimination der Unbekannten leicht ermittelt oder die Lösungsmenge abgelesen werden kann. Die Anzahl der benötigten Operationen ist von der Größenordnung ${\displaystyle n^{3}}$ bei einer ${\displaystyle n\times n}$-Matrix. In seiner Grundform ist der Algorithmus anfällig für Rundungsfehler, aber mit kleinen Modifikationen (Pivotisierung) stellt er für allgemeine lineare Gleichungssysteme das Standardlösungsverfahren dar. ↪ zum Artikel

Geometrisierung von 3-Mannigfaltigkeiten

Die Idee der Geometrisierung wurde 1980 von William Thurston als ein Programm zur Klassifizierung geschlossener 3-dimensionaler Mannigfaltigkeiten vorgestellt. Das Ziel der Geometrisierung ist, nach der Zerlegung einer 3-Mannigfaltigkeit in Grundbausteine auf jedem dieser Bausteine eine charakteristische geometrische Struktur zu finden. Die von Thurston aufgestellte Vermutung, dass dies immer möglich ist, stellt eine Verallgemeinerung der Poincaré-Vermutung dar und wurde von Grisha Perelman mit seinen Arbeiten zum Ricci-Fluss bewiesen. ↪ zum Artikel

Geschichte der Mathematik

Die Geschichte der Mathematik reicht zurück bis ins Altertum. Die wichtigsten erhaltenen Quellen, die uns Auskunft über die mathematischen Fähigkeiten der Ägypter geben, sind der Papyrus Rhind, der Papyrus Moskau und die so genannte Lederrolle. Die Ägypter verwendeten die Mathematik hauptsächlich für praktische Aufgaben wie die Lohnberechnung, die Berechnung von Getreidemengen zum Brotbacken oder Flächenberechnungen. Sie kannten die vier Grundrechenarten durch Rückführung auf Addition, Stammbrüche und das Lösen von Gleichungen mit einer Variablen. ↪ zum Artikel

Geschichte der Wahrscheinlichkeitsrechnung

Die Geschichte der Wahrscheinlichkeitsrechnung oder Stochastik beschreibt die Entwicklung eines gleichzeitig alten und modernen Teilgebiets der Mathematik, das sich mit der mathematischen Analyse von Experimenten mit unsicherem Ausgang befasst. Während viele heute noch gebräuchliche Formeln zu einfachen Zufallsprozessen möglicherweise bereits im Altertum, spätestens jedoch im ausgehenden Mittelalter bekannt waren, hat sich das heute verwendete axiomatische Fundament der Wahrscheinlichkeitstheorie erst zu Beginn des 20. Jahrhunderts herausgebildet. ↪ zum Artikel

Hamming-Code

Der Hamming-Code ist ein von Richard Hamming entwickelter linearer fehlerkorrigierender Blockcode, der in der digitalen Signalverarbeitung und der Nachrichtentechnik zur gesicherten Datenübertragung oder Datenspeicherung verwendet wird. Die Besonderheit dieses Codes besteht in der Verwendung mehrerer Paritätsbits. Diese Bits ergänzen jeweils unterschiedlich gewählte Gruppen von den die Information tragenden Nutzdatenbits. Durch eine geschickte Wahl der Gruppierung ist nicht nur eine Fehlererkennung, sondern auch eine Fehlerkorrektur der übertragenden Datenbits möglich. ↪ zum Artikel

Infinite monkey theorem

(c) Kosmopolitat, CC-BY-SA-3.0

Das Infinite monkey theorem (v. engl. infinite, „unendlich“; monkey, „Affe“; theorem, „Theorem“, „Lehrsatz“) besagt, dass ein einzelner Affe, der unendlich lange zufällig auf einer Tastatur herumtippt, mit an Sicherheit grenzender Wahrscheinlichkeit irgendwann alle Bücher in der französischen Bibliothèque nationale de France (Nationalbibliothek Frankreichs) schreiben wird. In englischsprachigen Ländern geht man davon aus, dass so irgendwann die Werke William Shakespeares entstehen werden. ↪ zum Artikel

Kettenbruch

In der Mathematik und insbesondere der Zahlentheorie ist ein Kettenbruch (fortgesetzter Bruch) ein Ausdruck der Form ${\displaystyle a+{\tfrac {b}{c+{\tfrac {d}{e+\ldots }}}}}$. Ein Kettenbruch ist also ein gemischter Bruch der Form ${\displaystyle a+{\tfrac {b}{x}}}$, bei dem der Nenner x wieder die Form eines gemischten Bruchs besitzt, wobei sich dieser Aufbau weiter so fortsetzt. Kettenbrüche kommen in der Zahlentheorie zur Anwendung und ebenso in der Kryptographie, algebraischen Geometrie, Topologie, Funktionentheorie und numerischen Mathematik. ↪ zum Artikel

Mandelbrot-Menge

Die Mandelbrot-Menge, im allgemeinen Sprachgebrauch oft auch Apfelmännchen genannt, ist ein Fraktal, das in der Chaostheorie eine bedeutende Rolle spielt. Es wurde 1980 von Benoît Mandelbrot erstmals computergrafisch dargestellt und untersucht. Die mathematischen Grundlagen dafür wurden bereits 1905 von dem französischen Mathematiker Pierre Fatou erarbeitet. Außerhalb der Fachwelt wurde die Mandelbrot-Menge vor allem durch den hohen ästhetischen Reiz dieser Computergrafiken bekannt, der durch geschickte Farbgestaltung des Außenbereichs, der nicht zur Menge gehört, noch erhöht wird. Die Mandelbrot-Menge wird oft als das formenreichste geometrische Gebilde bezeichnet, das überhaupt bekannt ist. ↪ zum Artikel

Mathematik

Die Mathematik (griechisches Adjektiv μαθηματική [τέχνη], mathēmatikē [téchnē], „[die Kunst des] Lernen[s], zum Lernen gehörig“; vom altgriechischen Verb μανθάνω, manthánō, „ich lerne“) ist die Wissenschaft, welche aus der Untersuchung von Figuren und dem Rechnen mit Zahlen entstand. Für Mathematik gibt es keine allgemein anerkannte Definition; heute wird sie üblicherweise als eine Wissenschaft, die selbstgeschaffene abstrakte Strukturen auf ihre Eigenschaften und Muster untersucht, beschrieben. ↪ zum Artikel

Methode der kleinsten Quadrate

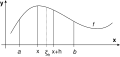
Die Methode der kleinsten Quadrate (bezeichnender auch: der kleinsten Fehlerquadrate; englisch: Least Squares Method) ist das mathematische Standardverfahren zur Ausgleichungsrechnung. Es ist eine Wolke aus Datenpunkten gegeben, die physikalische Messwerte, wirtschaftliche Größen usw. repräsentieren können. In diese Punktwolke soll eine möglichst genau passende, parameterabhängige Modellkurve gelegt werden. Dazu bestimmt man die Parameter dieser Kurve numerisch, indem die Summe der quadratischen Abweichungen der Kurve von den beobachteten Punkten minimiert wird. ↪ zum Artikel

Newton-Verfahren

Das Newtonsche Näherungsverfahren, auch Newton-Raphsonsche Methode, (benannt nach Sir Isaac Newton 1669 und Joseph Raphson 1690) ist in der Mathematik das Standardverfahren zur numerischen Lösung von nichtlinearen Gleichungen und Gleichungssystemen. Im Falle einer Gleichung mit einer Variablen lassen sich zu einer gegebenen stetig differenzierbaren Funktion f: R → R Näherungswerte zu Lösungen der Gleichung f(x)=0, d. h. Näherungen der Nullstellen dieser Funktion finden. Die grundlegende Idee dieses Verfahrens ist, die Funktion in einem Ausgangspunkt zu linearisieren, d. h. ihre Tangente zu bestimmen, und die Nullstelle der Tangente als verbesserte Näherung der Nullstelle der Funktion zu verwenden. ↪ zum Artikel

Produktregel

Die Produktregel oder Leibnizregel (nach G. W. Leibniz) ist eine grundlegende Regel der Differentialrechnung. Sie führt die Berechnung der Ableitung eines Produktes von Funktionen auf die Berechnung der Ableitung der einzelnen Funktionen zurück. Sind die Funktionen u(x) und v(x) von einem Intervall D in die reellen oder komplexen Zahlen an der Stelle xa aus D differenzierbar, so ist auch die Funktion f(x) = u(x) · v(x) an der Stelle x=xa differenzierbar, und es gilt: (uv)' = u'v + uv'. Eine Anwendung der Produktregel in der Integralrechnung ist die Methode der partiellen Integration. ↪ zum Artikel

Römische Zahlschrift

Als römische Zahlen bezeichnet man die Zahlzeichen einer in der römischen Antike entstandenen und noch heute für Nummern und besondere Zwecke gebräuchlichen Zahlschrift, in der in der heutigen Normalform die lateinischen Buchstaben I (1), V (5), X (10), L (50), C (100), D (500) und M (1000) als Zahlzeichen für die Schreibung der natürlichen Zahlen verwendet werden.

Es handelt sich um eine additive Zahlschrift, mit ergänzender Regel für die subtraktive Schreibung bestimmter Zeichen, aber ohne Stellenwertsystem und ohne Zeichen für Null. Zugrunde liegt ein kombiniert quinär-dezimales oder biquinäres Zahlensystem mit den Basiszahlen 5 und 10. ↪ zum Artikel

Rot-Schwarz-Baum

Ein Rot-Schwarz-Baum (engl. red–black tree oder RB tree) ist in der Informatik eine vom binären Suchbaum abgeleitete Datenstruktur, die sehr schnellen Zugriff auf die in ihr gespeicherten Werte garantiert. Rot-Schwarz-Bäume wurden zuerst 1972 von Rudolf Bayer beschrieben, welcher sie symmetric binary B-trees nannte. Der heutige Name geht auf Leo J. Guibas und Robert Sedgewick zurück, die 1978 die rot-schwarze Farbkonvention einführten. ↪ zum Artikel

Sammelbilderproblem

Das Sammelbilderproblem, Sammler-Problem, Sammelalben-Problem oder Problem der vollständigen Serie (englisch Coupon Collector’s Problem) befasst sich mit der Frage, wie viele Bilder einer Sammelbildserie zu kaufen sind, um ein Sammelalbum vervollständigen zu können. Beim klassischen Sammelbilderproblem geht man davon aus, dass alle Bilder verdeckt gekauft werden und alle Motive gleich häufig vorkommen. Die letztere Voraussetzung ist aber beispielsweise bei Sammelkartenspielen, auch „Trading Card Games“ genannt, nicht erfüllt, da hier das Vorkommen einzelner Karten stark variiert. Eine weitere wichtige Rolle spielt die Möglichkeit des Nachkaufens und Tauschens von Karten. Mit Hilfsmitteln der Wahrscheinlichkeitstheorie sowie Monte-Carlo-Simulationen können Sammelstrategien optimiert werden, um das Sammelalbum möglichst kostengünstig zu füllen. Das Sammelbilderproblem ist aufgrund der Beliebtheit der Fußball-Sammelalben eines der wenigen mathematischen Probleme, über das regelmäßig in den Massenmedien berichtet und diskutiert wird. ↪ zum Artikel

Schere, Stein, Papier

(c) Enzoklop, CC BY-SA 3.0

Schere, Stein, Papier (auch Schnick, Schnack, Schnuck; Ching, Chang, Chong; Klick, Klack, Kluck; Stein schleift Schere; Schnibbeln, Knobeln oder Schniekern) ist ein weltweit verbreitetes Knobelspiel, das sowohl bei Kindern als auch Erwachsenen beliebt ist. Jeder der beiden Kontrahenten entscheidet sich für ein Symbol, welches gleichzeitig mit der Hand dargestellt wird. Da jedes Symbol gegen eines der anderen gewinnen und gegen ein anderes verlieren kann, ist der Spielausgang ungewiss, da kein Spieler weiß, für welche Symbole sich die anderen Spieler entscheiden werden. ↪ zum Artikel

Sierpinski-Dreieck

Ein Sierpinski-Dreieck (nach Wacław Sierpiński) ist ein Fraktal, das durch fortgesetzte rekursive Aufteilung eines Vorgängerdreiecks n-1 in vier weitere (zueinander kongruente) Dreiecke erhalten wird, die dem Ausgangsdreieck ähnlich im mathematischen Sinne sind. Geht n gegen unendlich, spricht man von einer Sierpinski-Fläche. Die fraktale Dimension der Sierpinski-Fläche beträgt D = log 3/log 2 = 1,585... ↪ zum Artikel

Solow-Modell

Das Solow-Modell (auch Solow-Swan-Modell) ist ein 1956 von Robert Merton Solow und Trevor Swan entwickeltes Modell, welches einen Beitrag dazu leistet, das ökonomische Wachstum einer Volkswirtschaft mathematisch zu erklären. Es stellt ein exogenes Wachstumsmodell dar und bildet eine Grundlage der neoklassischen Wachstumstheorie. Aufgrund seiner besonderen attraktiven mathematischen Eigenschaften und der mathematischen Einfachheit erwies sich das Solow-Modell als ein geeigneter Ausgangspunkt für verschiedenste Erweiterungen. ↪ zum Artikel

Stellenwertsystem

(c) Alexander Jones & Eric Pierce, CC-BY-SA-3.0

Ein Stellenwertsystem (auch Positionssystem genannt) ist ein Zahlensystem, das im Vergleich zu Additionssystemen mit wenigen Symbolen (meist Ziffern oder Zahlzeichen genannt) große Zahlen darstellt. In diesem Zusammenhang wird auch oft von der b-adischen Darstellung von Zahlen (nicht zu verwechseln mit p-adischen Zahlen) gesprochen, wobei die Variable b für die Anzahl der Symbole steht. Der Wert von b wird in diesem Zusammenhang auch oft als Basis oder Grundzahl bezeichnet. Beispiele für Stellenwertsysteme sind das im Alltag gewöhnlich gebrauchte Dezimalsystem (dekadisches System mit der Grundzahl 10), das Dualsystem (dyadisches System mit der Grundzahl 2) und das Hexadezimalsystem (hexadekadisches System mit der Grundzahl 16). Ein Beispiel für ein Zahlensystem, das kein Stellenwertsystem ist, ist das der römischen Ziffern. Es handelt sich dabei um ein Additionssystem. ↪ zum Artikel

Sudoku

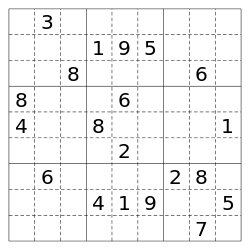
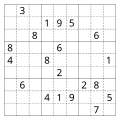
Sudoku (jap. 数独 Sūdoku, kurz für 数字は独身に限る Sūji wa dokushin ni kagiru, wörtlich so viel wie „Isolieren Sie die Zahlen“) ist ein Logikrätsel und ähnelt lateinischen Quadraten. In der üblichen Version ist es das Ziel, ein 9×9-Gitter mit den Ziffern 1 bis 9 so zu füllen, dass jede Ziffer in jeder Spalte, in jeder Zeile und in jedem Block (3×3-Unterquadrat) genau einmal vorkommt. Ausgangspunkt ist ein Gitter, in dem bereits mehrere Ziffern vorgegeben sind. In Zeitungen und Zeitschriften werden heute regelmäßig Sudokurätsel veröffentlicht. ↪ zum Artikel

Theorie der endlichen Kugelpackungen

Die Theorie der endlichen Kugelpackungen ist ein Gebiet der Mathematik, welches sich mit der Frage beschäftigt, wie eine endliche Menge von Kugeln optimal, also möglichst platzsparend, verpackt werden kann. Endliche Kugelpackungen sind erst in den letzten Jahrzehnten mathematisch genauer untersucht worden. Fejes Tóth hat dazu wichtige Grundsteine gelegt. Eine weitaus längere Tradition haben dagegen unendliche Kugelpackungen. Das Problem der dichtesten Anordnung kann man auch für eine unendliche Anzahl von Kugeln betrachten. Hier geht es darum, diejenige Anordnung von Kugeln zu finden, bei der am wenigsten Zwischenraum bleibt. Die berühmteste Vermutung hierzu ist die Keplersche Vermutung. Kugelpackungen haben ihre Anwendung in der Kristallografie. ↪ zum Artikel

Varianz

Die Varianz (lateinisch variantia für „Verschiedenheit“), veraltet auch Dispersion (lat. dispersio „Zerstreuung“, von dispergere „verteilen, ausbreiten, zerstreuen“) oder Streuung, ist die mittlere quadratische Abweichung einer reellen Zufallsvariablen von ihrem Erwartungswert. Sie ist das Quadrat der Standardabweichung, dem wichtigsten Streuungsmaß in der Stochastik. Die Varianz ist ein Maß für die Streuung der Wahrscheinlichkeitsdichte um ihren Schwerpunkt und kann physikalisch als Trägheitsmoment interpretiert werden. Mathematisch stellt die Varianz das zentrale Moment zweiter Ordnung einer Zufallsvariablen dar. ↪ zum Artikel

Vollständige Induktion

Vollständige Induktion oder der „Schluss von n auf n + 1“ ist eine mathematische Beweismethode, die üblicherweise eine Aussage für alle natürlichen Zahlen beweist (verallgemeinert). Sie funktioniert aber auch für allgemeinere Fälle (siehe unten). Der Name dieses Beweisverfahrens leitet sich ab von lat. inductio (= Herein- oder Hinaufführung, im Kontrast zu deductio Herabführung). Obwohl auch bei der vollständigen Induktion vom Speziellen auf das Allgemeine geschlossen wird, ist sie jedoch kein induktives, sondern ein deduktives Prinzip. ↪ zum Artikel

Zweitpreisauktion

Als (verdeckte) Zweitpreisauktion (englisch second-price [sealed bid] auction) bezeichnet man in der Auktionstheorie eine Form einer Auktion, bei der zwar der Höchstbietende den Zuschlag erhält, am Ende jedoch nur das zweithöchste Gebot zahlen muss. Dabei werden die Gebote jeweils einmalig so abgegeben, dass sie den anderen Bietern nicht bekannt werden („verdeckt“, wie bei der Abgabe in einem Umschlag, der erst nach Ende des Bietprozesses geöffnet wird). Nach ihrem theoretischen Begründer, dem Nobelpreisträger William Vickrey, bezeichnet man Zweitpreisauktionen auch als Vickreyauktionen. Zweitpreisauktionen sind abzugrenzen von den so genannten Erstpreisauktionen, die zwar dasselbe Format und einen identischen Allokationsmechanismus verwenden (der Höchstbietende gewinnt), bei denen der Gewinner aber auch das von ihm selbst abgegebene Gebot zahlen muss. ↪ zum Artikel

Lesenswerte Artikel zu Mathematikern

René Descartes

René Descartes, latinisiert Renatus Cartesius, (* 31. März 1596 in La Haye/Touraine, Frankreich; † 11. Februar 1650 in Stockholm, Schweden) war ein französischer Philosoph, Mathematiker und Naturwissenschaftler.

Descartes gilt als der Begründer des modernen frühneuzeitlichen Rationalismus, den Spinoza, Malebranche und Leibniz kritisch-konstruktiv weitergeführt haben. Sein rationalistisches Denken wird auch Cartesianismus genannt. Er ist außerdem für das berühmte Dictum „cogito ergo sum“ („ich denke, also bin ich“) bekannt, das die Grundlage seiner Metaphysik bildet aber auch das Selbstbewusstsein als genuin philosophisches Thema eingeführt hat. ↪ zum Artikel

Leonhard Euler

Leonhard Euler (lateinisch Leonhardus Eulerus; * 15. April 1707 in Basel; † 7. September [jul.]/ 18. September 1783 [greg.] in Sankt Petersburg) war ein Schweizer Mathematiker, Physiker, Astronom, Geograph, Logiker und Ingenieur. Er machte wichtige und weitreichende Entdeckungen in vielen Zweigen der Mathematik, wie beispielsweise der Infinitesimalrechnung und der Graphentheorie. Gleichzeitig leistete Euler fundamentale Beiträge auf anderen Gebieten wie der Topologie und der analytischen Zahlentheorie. Er prägte große Teile der bis heute weltweit gebräuchlichen mathematischen Terminologie und Notation. Beispielsweise führte Euler den Begriff der mathematischen Funktion in die Analysis ein. Er ist zudem für seine Arbeiten in der Mechanik, Strömungsdynamik, Optik, Astronomie und Musiktheorie bekannt. ↪ zum Artikel

Carl Friedrich Gauß

Johann Carl Friedrich Gauß (latinisiert Carolus Fridericus Gauss; * 30. April 1777 in Braunschweig; † 23. Februar 1855 in Göttingen) war ein deutscher Mathematiker, Astronom, Geodät und Physiker mit einem breit gefächerten Feld an Interessen. Er wird auch Fürst der Mathematik genannt, da ihn viele für den besten Mathematiker aller Zeiten halten. Im Alter von sieben Jahren kam Gauß in die Volksschule. Dort stellte sein Lehrer Büttner seinen Schülern die Aufgabe, die Zahlen von 1 bis 100 zu summieren, um diese zu beschäftigen. Gauß hatte sie allerdings nach kürzester Zeit gelöst, indem er 50 Paare der Summe 101 bildete (1 + 100, 2 + 99, ..., 50 + 51) und 5050 als Ergebnis erhielt. Die daraus resultierende Formel wird gelegentlich auch als „der kleine Gauß“ bezeichnet. ↪ zum Artikel

Kurt Gödel

Kurt Gödel (* 28. April 1906 in Brünn, Österreich-Ungarn, heute Brno, Tschechien; † 14. Januar 1978 in Princeton, New Jersey) war Mathematiker und Logiker. Gödel wird von vielen als der bedeutendste Logiker des 20. Jahrhunderts angesehen. Er hat maßgebliche Beiträge im Bereich der Prädikatenlogik (Entscheidungsproblem) sowie zum klassischen und intuitionistischen Aussagenkalkül geleistet. ↪ zum Artikel

Felix Hausdorff

Felix Hausdorff (* 8. November 1868 in Breslau; † 26. Januar 1942 in Bonn) war ein deutscher Mathematiker. Er gilt als Mitbegründer der modernen Topologie und lieferte wesentliche Beiträge zur allgemeinen und deskriptiven Mengenlehre, zur Maßtheorie, Funktionalanalysis und Algebra. Neben seinem Beruf wirkte er unter dem Pseudonym Paul Mongré auch als philosophischer Schriftsteller und Literat. ↪ zum Artikel

David Hilbert

David Hilbert (* 23. Januar 1862 in Königsberg; † 14. Februar 1943 in Göttingen) war einer der bedeutendsten Mathematiker der Neuzeit. Viele seiner Arbeiten in Mathematik und mathematischer Physik begründeten eigenständige Forschungsgebiete. Seine Vorschläge zu den Grundlagen der Mathematik („Hilbertprogramm“) führten zu einer kritischen Analyse der Begriffsdefinitionen der Mathematik und des mathematischen Beweises. Hilberts programmatische Rede auf dem internationalen Mathematikerkongress in Paris im Jahre 1900, in der er eine Liste von 23 mathematischen Problemen vorstellte, beeinflusste die mathematische Forschung des 20. Jahrhunderts nachhaltig. ↪ zum Artikel

Johannes Kepler

Johannes Kepler (lateinisch Ioannes Keplerus, auch Keppler; * 27. Dezember 1571 in Weil der Stadt; † 15. November 1630 in Regensburg) war ein deutscher Naturphilosoph, Mathematiker, Astronom, Astrologe, Optiker und evangelischer Theologe.

Johannes Kepler entdeckte die Gesetzmäßigkeiten, nach denen sich Planeten um die Sonne bewegen. Sie werden nach ihm Keplersche Gesetze genannt. In der Mathematik wurde ein numerisches Verfahren zur Berechnung von Integralen nach ihm Keplersche Fassregel benannt. Mit seiner Einführung in das Rechnen mit Logarithmen trug Kepler zur Verbreitung dieser Rechenart bei. ↪ zum Artikel

Sofja Kowalewskaja

Sofja Kowalewskaja (russisch Софья Васильевна Ковалевская, wiss. Transliteration Sofja Vasiljevna Kovalevskaja; * 3. Januar / 15. Januar 1850 in Moskau; † 29. Januar / 10. Februar 1891 in Stockholm) war eine russische Mathematikerin. Zu Sofja Kowalewskaja gibt es viele verschiedene Namensversionen: In englischen Arbeiten heißt sie meistens Sofia Kovalevskaia oder Kovalevskaya; weil in den westeuropäischen Ländern unbekannt war, dass es in Russland auch eine weibliche Form des Nachnamens gibt, wird sie in Westeuropa bis heute häufig unter dem Namen ihres Mannes Kowalewski (auch Kowalewsky oder Kovalewsky) geführt; ihr Vorname wurde in Deutschland zumeist zu Sonja, in Frankreich zu Sophie. ↪ zum Artikel

Emanuel Lasker

(c) Bundesarchiv, Bild 102-00457 / CC-BY-SA 3.0

Emanuel Lasker (* 24. Dezember 1868 in Berlinchen, Neumark; † 11. Januar 1941 in New York) war ein deutscher Schachspieler, Mathematiker und Philosoph. Er war der zweite offizielle Schachweltmeister und zugleich der bislang einzige deutsche Träger dieses Titels. Er behauptete diese Position über einen Zeitraum von 27 Jahren (1894 bis 1921) und damit länger als jeder andere Schachweltmeister. 2008 wurde Emanuel Lasker in die Hall of Fame des deutschen Sports aufgenommen. ↪ zum Artikel

Paul Lorenzen

Paul Lorenzen (* 24. März 1915 in Kiel; † 1. Oktober 1994 in Göttingen) war ein deutscher Philosoph, Wissenschaftstheoretiker, Mathematiker und Logiker. Er ist neben Wilhelm Kamlah der Begründer der Erlanger Schule des methodischen Konstruktivismus.

Lorenzen orientierte seine Philosophie am pragmatischen Handeln und am Prinzip der Methodischen Ordnung. In der Logischen Propädeutik gestaltete er einen handlungstheoretischen und sprachphilosophischen Neuansatz. In der Dialogischen Logik erarbeite er ein eigenständiges System zur Argumentationstheorie. Weiterhin leistete er wichtige Beiträge zur Konstruktiven Mathematik und zur Modallogik. ↪ zum Artikel

Charles Sanders Peirce

Charles Sanders Peirce (* 10. September 1839 in Cambridge, Massachusetts, † 19. April 1914 in Milford, Pennsylvania) war ein US-amerikanischer Mathematiker, Philosoph und Logiker.

Peirce gehört neben William James und John Dewey zu den maßgeblichen Denkern des Pragmatismus; außerdem gilt er als Begründer der modernen Semiotik. Bertrand Russell bezeichnete ihn als den „größten amerikanischen Denker“, Karl Popper betrachtete ihn sogar als „einen der größten Philosophen aller Zeiten“. ↪ zum Artikel

Pythagoras

Pythagoras von Samos (griechisch Πυθαγόρας) (* um 570 v. Chr., † nach 510 v. Chr. in Metapont in der Basilicata) war ein antiker griechischer Philosoph und Gründer einer einflussreichen religiös-philosophischen Bewegung. Als Vierzigjähriger verließ er seine griechische Heimat und wanderte nach Unteritalien aus. Dort gründete er eine Schule und betätigte sich auch politisch. Trotz intensiver Bemühungen der Forschung gehört er noch heute zu den rätselhaftesten Persönlichkeiten der Antike. Manche Historiker zählen ihn zu den Pionieren der beginnenden griechischen Philosophie, Mathematik und Naturwissenschaft, andere meinen, er sei vorwiegend oder ausschließlich ein Verkünder religiöser Lehren gewesen. Möglicherweise konnte er diese Bereiche verbinden. Die nach ihm benannten Pythagoreer blieben auch nach seinem Tod kulturgeschichtlich bedeutsam. ↪ zum Artikel

Srinivasa Ramanujan

Srinivasa Ramanujan, (* 22. Dezember 1887 in Erode; † 26. April 1920 in Chetpet, Madras) war ein indischer Mathematiker. Er eignete sich seine mathematischen Kenntnisse autodidaktisch aus Fachliteratur an und besaß eine außerordentliche Begabung dafür, analytische und zahlentheoretische Probleme intuitiv zu lösen, meist ohne zunächst einen Lösungsweg oder Beweise angeben zu können. In der Schule wurden seine mathematischen Fähigkeiten gefördert, doch ein Studium scheiterte an seiner Spezialisierung. Am Existenzminimum lebend betrieb er die Mathematik privat und notierte seine Erkenntnisse in den sogenannten Notizbüchern. ↪ zum Artikel

Ludwig Wittgenstein

Ludwig Josef Johann Wittgenstein (* 26. April 1889 in Wien; † 29. April 1951 in Cambridge) war ein österreichisch-britischer Philosoph.

Er lieferte bedeutende Beiträge zur Philosophie der Logik, der Sprache und des Bewusstseins. Seine beiden Hauptwerke Logisch-philosophische Abhandlung (Tractatus Logico-Philosophicus, 1921) und Philosophische Untersuchungen (1953, postum) wurden zu wichtigen Bezugspunkten zweier philosophischer Schulen, des Logischen Positivismus und der Analytischen Sprachphilosophie. ↪ zum Artikel

Yoshida Mitsuyoshi

Yoshida Mitsuyoshi (japanisch 吉田 光由; * 1598; † 1672) war ein japanischer Mathematiker der Edo-Zeit. Er verfasste das weit verbreitete Rechenbuch Jinkōki (塵劫記; erschienen zwischen 1627 und 1641). Es wurde bis zu den europäisch orientierten Schulreformen zu Beginn der Meiji-Zeit unter anderem in den Terakoya-Schulen eingesetzt. Das Jinkōki gehört zum breitenwirksamsten Bereich der traditionellen japanischen Mathematik (和算, Wasan), der im Gegensatz zur mehr wissenschaftlich orientierten Expertenmathematik etwa der Seiki-Schule und den kultisch bedeutsamen Sangaku-Tafeln für den Hausgebrauch gedacht war. Zum praktischen Nutzen des Werks trugen auch die zahlreichen darin enthaltenen, wohl vom Autor entworfenen Zeichnungen bei. ↪ zum Artikel

Viri Mathematici

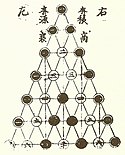
Viri Mathematici quos inclytum Viennense gymnasium ordine celebres habuit (deutsch Berühmte Mathematiker der Wiener Universität) ist der Titel von Georg Tannstetters lateinischer Darstellung der von 1384 bis zum Druckjahr 1514 in Wien tätigen Astronomen und Mathematiker. Dieser historische Rückblick, ein früher Ansatz einer Wissenschaftsgeschichte, erschien als einleitendes Kapitel einer Edition astronomischer Tabellen. Darin sind biographische Informationen zu insgesamt 32 Astronomen und Mathematikern enthalten. Bei fünf von ihnen sind umfangreiche Listen ihrer Werke hinzugefügt: Johannes von Gmunden, Georg von Peuerbach, Johannes Regiomontanus, Johannes Stabius und Andreas Stiborius. Insgesamt enthält dieser Rückblick etwa 170 Buchtitel zu überwiegend mathematischen und astronomischen Themen. ↪ zum Artikel

Georg Tannstetter

Georg Tannstetter, Humanistenname Collimitius (1482-1535) war an der Wiener Universität Professor für angewandte Mathematik, außerdem königlicher Leibarzt im Dienst mehrerer habsburgischer Regenten. Seine Darstellung der Geschichte der Wiener Mathematiker und Astronomen (Viri Mathematici) ist ein früher Ansatz zur Naturwissenschaftsgeschichtsschreibung. Gemeinsam mit einem Schüler entwarf er eine Ungarnkarte, die zum Weltdokumentenerbe gehört. Seine Vorlesung zur „Iatromathematik“, der Anwendung astrologischer Regeln auf die Medizin, wurde gedruckt. 1515 veröffentlichte er für den mathematischen Unterricht eine Sammlung spätmittelalterlicher mathematischer Abhandlungen. ↪ zum Artikel

Informative Listen

Liste bedeutender Mathematiker

Liste kleiner Gruppen

Liste univariater Wahrscheinlichkeitsverteilungen

Siehe auch

• Exzellenzinitiative Mathematik
• Weitere lesenswerte Artikel in der Wikipedia
• Weitere informative Listen in der Wikipedia