Portal:Mathematik/Exzellente Artikel

Übersicht

Qualitätssicherung

Projekt

Exzellente Artikel

Lesenswerte Artikel

Portal:Mathematik

Allgemein

• Portalseite
• Diskussionsseite

Mitarbeit

• Qualitätssicherung
• Arbeitslisten
• Exzellenzinitiative
• Fehlende Artikel
• Artikel ohne Quellenangaben
• Verwaiste Artikel

Projekt

• Hinweise zur Mitarbeit
• Projektinterna
• Portalchat
• Ansprechpartner
• Artikelcharts
• Kategorienbaum Mathematik
• Quellen im Web

Siehe auch

• Literaturstipendium
• Hilfe zu TeX

Commons: Mathematik

Beweisarchiv

Algorithmensammlung

Exzellente Artikel zu mathematischen Themen

Ackermannfunktion

Die Ackermannfunktion ist eine 1926 von Wilhelm Ackermann gefundene, extrem schnell wachsende mathematische Funktion, mit deren Hilfe in der theoretischen Informatik Grenzen von Computer- und Berechnungsmodellen aufgezeigt werden können. Heute gibt es eine ganze Reihe von Funktionen, die als Ackermannfunktion bezeichnet werden. Diese weisen alle ein ähnliches Bildungsgesetz wie die ursprüngliche Ackermannfunktion auf und haben auch ein ähnliches Wachstumsverhalten. ↪ zum Artikel

Bestimmtheitsmaß

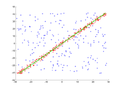
Das Bestimmtheitsmaß, auch Determinationskoeffizient (von lateinisch determinatio „Abgrenzung, Bestimmung“, bzw. determinare „eingrenzen“, „festlegen“, „bestimmen“ und coefficere „mitwirken“), ist in der Statistik eine wichtige Kennzahl zur formalen Beurteilung der Anpassungsgüte einer Regression. Das Bestimmtheitsmaß beruht auf der Streuungszerlegung, bei der die gesamte Variation der abhängigen Variablen in die (durch das Regressionsmodell) erklärte Variation und in die Variation der Residuen zerlegt wird. In der einfachen und multiplen linearen Regression ist das Bestimmtheitsmaß definiert als Verhältnis der „durch die Regression erklärten Variation“ zur „gesamten zu erklärenden Variation“ und zeigt, wie viel Variation in den Daten durch ein vorliegendes lineares Regressionsmodell „erklärt“ werden kann. ↪ zum Artikel

Differentialrechnung

(c) ​German Wikipedia Benutzer Honina, CC-BY-SA-3.0

Die Differential- oder Differenzialrechnung ist ein wesentlicher Bestandteil der Analysis und damit ein Gebiet der Mathematik. Zentrales Thema der Differentialrechnung ist die Berechnung lokaler Veränderungen von Funktionen. Während eine Funktion ihren Eingabewerten nach tabellarischem Prinzip gewisse Ausgangswerte zuordnet, wird durch die Differentialrechnung ermittelt, wie stark sich die Ausgabewerte nach sehr kleinen Veränderungen der Eingabewerte ändern. Sie ist eng verwandt mit der Integralrechnung, mit der sie gemeinsam unter der Bezeichnung Infinitesimalrechnung zusammengefasst wird. ↪ zum Artikel

Dreiteilung des Winkels

Unter der Dreiteilung des Winkels (auch: Trisektion des Winkels) versteht man in der Geometrie das Problem, ob man einen beliebigen Winkel nur mit Hilfe von Zirkel und Lineal (den euklidischen Werkzeugen) konstruktiv und präzise in drei gleich große Winkel unterteilen kann. Die Dreiteilung des Winkels gehört zu den drei klassischen Problemen der antiken Mathematik und ist nur für bestimmte Winkel durchführbar. ↪ zum Artikel

Einschrittverfahren

Einschrittverfahren sind in der numerischen Mathematik neben den Mehrschrittverfahren eine große Gruppe von Rechenverfahren zur Lösung von Anfangswertproblemen. Diese Aufgabenstellung, bei der eine gewöhnliche Differentialgleichung zusammen mit einer Startbedingung gegeben ist, spielt in allen Natur- und Ingenieurwissenschaften eine zentrale Rolle und gewinnt beispielsweise auch in den Wirtschafts- und Sozialwissenschaften immer mehr an Bedeutung. Anfangswertprobleme werden verwendet, um dynamische Vorgänge zu analysieren, zu simulieren oder vorherzusagen.

Die namensgebende Grundidee der Einschrittverfahren ist, dass sie ausgehend von dem gegebenen Anfangspunkt Schritt für Schritt entlang der gesuchten Lösung Näherungspunkte berechnen. Dabei verwenden sie jeweils nur die zuletzt bestimmte Näherung für den nächsten Schritt, im Gegensatz zu den Mehrschrittverfahren, die auch weiter zurückliegende Punkte in die Rechnung miteinbeziehen. ↪ zum Artikel

Epipolargeometrie

Bei der Aufnahme eines Objekts oder einer Szene aus zwei Kamerapositionen beschreibt die Epipolargeometrie die geometrische Beziehung korrespondierender Bildpunkte, also der beiden Bildpunkte eines Objektpunktes, in den beiden Bildern.

Aus den zwei Aufnahmen eines Objekts von unterschiedlichen Kamerapositionen kann das Objekt dreidimensional rekonstruiert werden. Dazu müssen korrespondierende Bildpunkte eines Objektpunktes einander zugeordnet werden. Mit Hilfe der Epipolargeometrie kann eine einfache Beziehung zwischen korrespondierenden Punkte ohne Kenntnis der Kameraposition hergestellt werden. ↪ zum Artikel

Heegner-Punkt

Heegner-Punkte (benannt nach Kurt Heegner) sind Zahlen, die quadratische Gleichungen mit ganzzahligen Koeffizienten lösen, und die mit Punkten auf geometrischen Figuren, nämlich Modulkurven, verknüpft werden können. Die mittels der Verknüpfung gegebenen Punkte auf Modulkurven werden ebenfalls Heegner-Punkte genannt und sind Gegenstand der arithmetischen Geometrie. Sie spielen eine bedeutende Rolle in der Theorie der elliptischen Kurven und in der Klassenkörpertheorie. Heegner-Punkte unterscheiden sich von den namensähnlichen Heegner-Zahlen. ↪ zum Artikel

Holomorphe Funktion

In der Mathematik sind holomorphe Funktionen (von gr. ὅλος holos, „ganz“ und μορφή morphe, „Form“) komplexwertige Funktionen (Abbildungen von komplexen Zahlen in komplexe Zahlen), die in der Funktionentheorie, einem Teilgebiet der Mathematik, untersucht werden. Eine komplexwertige Funktion mit Definitionsbereich ${\displaystyle U}$ heißt holomorph, falls sie an jeder Stelle von ${\displaystyle U}$ komplex differenzierbar ist. Die aus der Schulmathematik bekannten Rechenregeln zum Ableiten vormals reeller Funktionen gelten dabei weiterhin für komplexe Funktionen, obgleich der Holomorphiebegriff viel weitreichendere Konsequenzen nach sich zieht. Anschaulich bedeutet Holomorphie, dass sich die betroffene Funktion an jeder Stelle „fast“ wie eine aus mathematischer Sicht leicht zu verstehende (komplexwertige) lineare Funktion verhält. Erstmals eingeführt und studiert wurden holomorphe Funktionen im 19. Jahrhundert von Augustin-Louis Cauchy, Bernhard Riemann und Karl Weierstraß, obgleich sich die Terminologie der Holomorphie erst im 20. Jahrhundert flächendeckend durchsetzte. Besonders in älterer Literatur werden solche Funktionen auch „regulär“ genannt. Aufgrund ihrer breiten Anwendungsmöglichkeiten zählen sie zu den wichtigsten Funktionstypen innerhalb der Mathematik. ↪ zum Artikel

Kreiszahl

Die Kreiszahl π (pi) ist eine mathematische Konstante; ihr Wert beträgt näherungsweise 3,141592. Sie beschreibt in der Geometrie das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser. Dieses Verhältnis ist unabhängig von der Größe des Kreises. Die Kreiszahl wird mit dem kleinen griechischen Buchstaben π bezeichnet, dem Anfangsbuchstaben des griechischen Wortes perifereia (Randbereich) bzw. perimeter (Umfang). Die Bezeichnung π erschien erstmals 1706 in dem Buch Synopsis palmariorum mathesos des aus Wales stammenden Gelehrten William Jones (1675–1749). Sie wird auch Archimedes-Konstante oder Ludolphsche Zahl (nach Ludolph van Ceulen) genannt. ↪ zum Artikel

Malfatti-Kreis

Die drei Malfatti-Kreise, später bekannt als Malfattisches Problem, sind benannt nach Gianfrancesco Malfatti, der 1803 ihre Konstruktion angab. Bestimmt sind die Malfatti-Kreise – unabhängig von der Form des Ausgangsdreiecks – durch drei Kreise in einem Dreieck mit der Eigenschaft, dass jeder die beiden anderen Kreise von außen und zwei Dreiecksseiten von innen berührt. Malfatti nahm fälschlich an, dass diese Eigenschaft der Kreise das Problem lösen, drei Kreise überschneidungsfrei so in ein Dreieck zu packen, dass sie maximalen Flächeninhalt haben. Warum die Malfatti-Kreise dieses sogenannte Malfatti’sche Maximierungsproblem, sprich die maximale Bedeckung der Dreiecksfläche durch drei Kreise, nicht lösen, lässt sich z. B. leicht an einem langen schmalen rechtwinkligen Dreieck erkennen. ↪ zum Artikel

Marshallsche Nachfragefunktion

Als marshallsche Nachfragefunktion (auch walrasianische Nachfragefunktion), benannt nach dem Ökonomen Alfred Marshall (bzw. Léon Walras), bezeichnet man in der Mikroökonomik und dort speziell in der Haushaltstheorie eine mathematische Funktion, die für gegebene Güterpreise und ein gegebenes Einkommen angibt, welche Menge von jedem einzelnen Gut konsumiert werden sollte, wenn man den größtmöglichen Nutzen realisieren möchte. ↪ zum Artikel

Mathematik in der Blütezeit des Islam

Die Mathematik in der Blütezeit des Islam basierte auf den Erkenntnissen der antiken griechischen und der indischen Mathematik, fügte diesen in der Zeit zwischen dem 8. und 13. Jahrhundert aber auch zahlreiche Neuerungen und Weiterentwicklungen hinzu. Während zeitgleich die Werke der Antike im frühmittelalterlichen christlichen Europa fast vergessen waren und dort kaum nennenswerte wissenschaftliche Fortschritte erzielt wurden, bewahrten die Gelehrten in der islamischen Welt die Kontinuität der mathematischen Forschung. Aus diesem Grunde spielen sie für die Geschichte der Mathematik eine wichtige Rolle. Bedeutende Mathematiker in der Blütezeit des Islam waren beispielsweise al-Chwarizmi, Thabit ibn Qurra, al-Battani, Abu l-Wafa, Alhazen und Omar Chayyam. ↪ zum Artikel

Numerische lineare Algebra

Die numerische lineare Algebra ist ein zentrales Teilgebiet der numerischen Mathematik. Sie beschäftigt sich mit der Entwicklung und der Analyse von Rechenverfahren (Algorithmen) für Problemstellungen der linearen Algebra, insbesondere der Lösung von linearen Gleichungssystemen und Eigenwertproblemen. Solche Probleme spielen in allen Natur- und Ingenieurwissenschaften, aber auch in der Ökonometrie und in der Statistik eine große Rolle. ↪ zum Artikel

Quadratur des Kreises

Die Quadratur des Kreises ist ein klassisches Problem der Geometrie. Die Aufgabe besteht darin, aus einem gegebenen Kreis in endlich vielen Schritten ein Quadrat mit dem gleichen Flächeninhalt zu konstruieren. Sie ist äquivalent zur sogenannten Rektifikation des Kreises, also der Konstruktion einer geraden Strecke, die dem Kreisumfang entspricht. Das wiederum entspricht der Konstruktion der Kreiszahl ${\displaystyle \pi }$ aus der Strecke 1. Beschränkt man die Konstruktionsmittel auf Lineal und Zirkel, so ist die Aufgabe aufgrund der Transzendenz von ${\displaystyle \pi }$ unlösbar; dies konnte 1882 von dem deutschen Mathematiker Ferdinand von Lindemann bewiesen werden. ↪ zum Artikel

Problem des Handlungsreisenden

Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein kombinatorisches Optimierungsproblem des Operations Research und der theoretischen Informatik. Die Aufgabe besteht darin, eine Reihenfolge für den Besuch mehrerer Orte so zu wählen, dass die gesamte Reisestrecke des Handlungsreisenden nach der Rückkehr zum Ausgangsort möglichst kurz ist.

Komplexitätstheoretisch gehört das TSP zur Klasse der NP-äquivalenten Probleme. Es wird daher sehr stark angenommen, dass die Laufzeit jedes deterministischen Algorithmus, der für dieses Problem stets optimale Lösungen liefert, im schlimmsten Fall exponentiell von der Anzahl der Städte abhängt. Schon für wenige Städte kann die benötigte Laufzeit eines solchen Algorithmus also unpraktikabel viel Zeit beanspruchen. ↪ zum Artikel

RANSAC-Algorithmus

Der RANSAC-Algorithmus (Random Sample Consensus, deutsch etwa „Übereinstimmung mit einer zufälligen Stichprobe“) ist ein Algorithmus zur Detektion von Ausreißern und groben Fehlern innerhalb einer Reihe von Messwerten. Er wurde 1981 von Martin A. Fischler und Robert C. Bolles vorgestellt. Oft liegen als Ergebnis einer Messung Datenpunkte vor, die physikalische Messwerte wie Druck, Entfernung oder Temperatur, wirtschaftliche Größen oder Ähnliches repräsentieren. In diese Punkte soll eine möglichst genau passende, parameterabhängige Modellkurve gelegt werden. Der RANSAC-Algorithmus erstellt mit Hilfe eines iterativen Verfahrens diese Modellkurve. ↪ zum Artikel

Riemannsche Vermutung

Die Riemannsche Vermutung, Riemannsche Hypothese, Riemannhypothese oder kurz RH trifft eine Aussage über die Verteilung der Primzahlen und ist eines der bedeutendsten ungelösten Probleme der Mathematik. Sie wurde erstmals 1859 von Bernhard Riemann in seiner Arbeit Über die Anzahl der Primzahlen unter einer gegebenen Größe in einem Nebensatz formuliert. Nachdem sie bereits im Jahr 1900 von David Hilbert auf seine Liste 23 wichtiger Jahrhundertprobleme gesetzt worden war, wurde sie im Jahr 2000 vom Clay Mathematics Institute in die Liste der sieben Millennium-Probleme der Mathematik aufgenommen. Das Institut in Cambridge (Massachusetts) hat damit ein Preisgeld von einer Million US-Dollar für eine schlüssige Lösung des Problems in Form eines mathematischen Beweises ausgelobt.

↪ zum Artikel

Riemannsche Zeta-Funktion

Die Riemannsche Zeta-Funktion ist eine komplexwertige, spezielle mathematische Funktion, die in der analytischen Zahlentheorie, einem Teilgebiet der Mathematik, eine wichtige Rolle spielt. Erstmals betrachtet wurde sie im 18. Jahrhundert von Leonhard Euler, der sie im Rahmen des Basler Problems untersuchte. Bezeichnet wird sie üblicherweise mit dem Symbol ${\displaystyle \zeta (s)}$ (mit dem Buchstaben Zeta), wobei ${\displaystyle s}$ eine komplexe Zahl ihres Definitionsbereichs ist. Für Werte ${\displaystyle s\in \mathbb {C} }$ mit Realteil größer als 1 wird die Riemannsche Zeta-Funktion über eine Dirichlet-Reihe definiert. Mittels analytischer Fortsetzung kann sie zu einer auf ${\displaystyle \mathbb {C} \setminus \{1\}}$ holomorphen Funktion ausgeweitet werden. Sie erfüllt eine wichtige Funktionalgleichung, mit deren Hilfe sie sogar charakterisiert werden kann. ↪ zum Artikel

Satz des Euklid

Der Satz des Euklid, manchmal auch Satz von Euklid, ist ein Lehrsatz aus der elementaren Zahlentheorie und besagt, dass es unendlich viele Primzahlen gibt. Benannt ist er nach Euklid von Alexandria, der ihn als Erster im dritten Jahrhundert v. Chr. in seinen Elemente (Euklid)|Elementen bewies. Jedoch kannten die Mathematiker der Antike das Konzept der Unendlichkeit noch nicht. Euklid selbst formulierte den Satz daher wie folgt: „Es gibt mehr Primzahlen als jede vorgelegte Anzahl von Primzahlen“. Der ursprüngliche von Euklid geführte Beweis ist direkt und konstruktiv. Zu einer gegebenen endlichen Liste von Primzahlen wird stets eine weitere noch nicht vorhandene Primzahl erzeugt, ohne diese jedoch explizit anzugeben. Vielmehr wird argumentiert, dass jede endliche Liste von Primzahlen unvollständig ist. Daraus wird gefolgert, dass es unendlich viele Primzahlen gibt. In der späteren Literatur wird oft fälschlicherweise behauptet, dass Euklids Argument anhand eines Widerspruchsbeweises aufgeführt sei. Jedoch lässt sich der Beweis leicht zu einem Widerspruchsbeweis umformulieren.↪ zum Artikel

Satz des Pythagoras

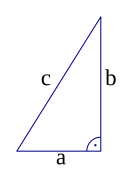
Der Satz des Pythagoras ist einer der fundamentalen Sätze der euklidischen Geometrie. Er besagt, dass in allen ebenen rechtwinkligen Dreiecken die Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates ist. Als Gleichung ausgedrückt lautet er a²+b²=c², wobei a und b wie im Bild für die Längen der am rechten Winkel anliegenden Seiten, der Katheten, stehen und die Länge der dem rechten Winkel gegenüberliegenden Seite, der Hypotenuse, darstellt. In der modernen Mathematik motiviert der Satz das Konzept des Senkrechtstehens in abstrakten Räumen. Der nach Pythagoras von Samos benannte Satz ist theoretischer Ausdruck der von indischen, babylonischen und ägyptischen Baumeistern und Priestern entwickelten praktischen Kunst, bei Abmessungen von Feldern und Bauten mit Hilfe von Seilen präzise rechte Winkel zu erzielen. ↪ zum Artikel

Satz von Dirichlet (Primzahlen)

Der Satz von Dirichlet, gelegentlich auch Dirichletscher Primzahlsatz, benannt nach Peter Gustav Lejeune Dirichlet, ist eine Aussage aus dem mathematischen Teilgebiet der Zahlentheorie. Er besagt, dass eine aufsteigende arithmetische Progression unendlich viele Primzahlen enthält, wenn dies nicht aus trivialen Gründen unmöglich ist. Eine arithmetische Progression ist dabei eine Folge ganzer Zahlen, sodass zwei aufeinanderfolgende Glieder stets dieselbe Differenz haben. Den ersten vollständigen Beweis der Aussage lieferte Dirichlet im Jahr 1837. Dabei wurden erstmals rein analytische Methoden für die Gewinnung eines zahlentheoretischen Satzes verwendet. Die Vermutung über Primzahlen in arithmetischen Folgen stammt von Adrien-Marie Legendre aus dem Jahr 1798, der in seinem Lehrbuch der Zahlentheorie einen fehlerhaften Beweis gab, wie Dirichlet darlegte. Anwendung findet der Satz innerhalb der Zahlentheorie, etwa im Beweis des Satzes von Hasse-Minkowski. ↪ zum Artikel

Stochastische Analysis

Die stochastische Analysis ist ein Teilgebiet der Mathematik, genauer der Wahrscheinlichkeitstheorie. Sie beschäftigt sich mit der Verallgemeinerung von Begriffsbildungen, Aussagen und Modellen der Analysis auf stochastische Prozesse, also auf Funktionen, deren Werte zufällig sind. Im Zentrum der stochastischen Analysis stehen die Formulierung und die Untersuchung von stochastischen Integralen und, darauf aufbauend, von stochastischen Differentialgleichungen. Historisch geht das Fachgebiet auf Arbeiten des japanischen Mathematikers Kiyoshi Itō ab 1944 zurück. Anwendungen des Fachgebiets finden sich unter anderem in der Biologie, in der Physik und in den Ingenieurwissenschaften, vor allem aber in der Finanzmathematik. ↪ zum Artikel

Wissenschaftliches Werk Leonhard Eulers

Das wissenschaftliche Werk von Leonhard Euler ist das umfangreichste von einem Mathematiker jemals geschaffene. Es umfasst unter anderem grundlegende Resultate in den Bereichen Infinitesimalrechnung, Analysis, Mechanik, Astronomie, Geodäsie, Zahlentheorie, Algebra, Trigonometrie, Geometrie, Musiktheorie und Optik. Zu Eulers berühmtesten Resultaten zählen die Lösung des Basler Problems, der Polyedersatz und die Eulersche Identität, wobei letztere eine enge Verbindung zwischen zahlreichen fundamentalen mathematischen Konstanten zieht. Für diese und andere Ergebnisse erhielt Euler auch posthum viele Ehrungen. ↪ zum Artikel

Würfelverdoppelung

Die Würfelverdoppelung, auch bekannt als Delisches Problem, bezeichnet die geometrische Aufgabe, zu einem gegebenen Würfel einen zweiten Würfel zu konstruieren, der im Vergleich zum ersten Würfel das doppelte Volumen aufweist. Das Problem gehört zu den drei „klassischen Problemen der antiken Mathematik“ und wurde bereits im 5. Jahrhundert v. Chr. im antiken Griechenland formuliert. ↪ zum Artikel

Exzellente Artikel zu Mathematikern

Archytas von Tarent

Archytas von Tarent (griechisch Ἀρχύτας Archýtas; * wohl zwischen 435 und 410 v. Chr.; † wohl zwischen 355 und 350 v. Chr.) war ein antiker griechischer Philosoph, Mathematiker, Musiktheoretiker, Physiker, Ingenieur, Staatsmann und Feldherr.

Archytas wirkte in seiner Heimatstadt, der griechischen Kolonie Tarent in Apulien. Als Philosoph gehörte er zur Richtung der Pythagoreer. Bekannt ist er vor allem durch seine freundschaftliche Beziehung zu Platon, durch die angeblich von ihm erfundene fliegende Taube und durch ein Gedankenexperiment, mit dem er die Unendlichkeit des Universums beweisen wollte. Von seinen Schriften, die insbesondere Themen der Mathematik und der Musik behandelten, sind nur wenige Fragmente erhalten geblieben. ↪ zum Artikel

Lewis Carroll

Lewis Carroll (* 27. Januar 1832 in Daresbury im County Cheshire; † 14. Januar 1898 in Guildford im County Surrey; eigentlich Charles Lutwidge Dodgson) war ein britischer Schriftsteller des viktorianischen Zeitalters, Fotograf, Mathematiker und Diakon. Er ist der Autor der berühmten Kinderbücher Alice im Wunderland, Alice hinter den Spiegeln (oder Alice im Spiegelland) und The Hunting of the Snark.

Neben seiner Tätigkeit als Tutor für Mathematik verfasste Carroll unter seinem Realnamen verschiedene mathematische Abhandlungen und Bücher über Algebra, ebene algebraische Kurven, Trigonometrie, zwei Bücher über Euklid, ein zweibändiges Buch „Curiosa Matematica“ (1888, 1893), dessen zweiter Teil der Unterhaltungsmathematik gewidmet ist, sowie 1896 sein letztes Werk zur symbolischen Logik. ↪ zum Artikel

Augustin Louis Cauchy

Augustin Louis Cauchy (* 21. August 1789 in Paris; † 23. Mai 1857 in Sceaux) war ein französischer Mathematiker.

Als ein Pionier der Analysis entwickelte er die von Gottfried Wilhelm Leibniz und Sir Isaac Newton aufgestellten Grundlagen weiter und formulierte sie als Theorie, wobei er die fundamentalen Aussagen auch formal bewies. Insbesondere in der Funktionentheorie stammen viele zentrale Sätze von ihm. Seine fast 800 Publikationen decken im Großen und Ganzen die komplette Bandbreite der damaligen Mathematik ab. ↪ zum Artikel

Eratosthenes

Eratosthenes von Kyrene (griechisch Έρατοσθένης ὁ Κυρηναῖος; * zwischen 276 und 273 v. Chr. in Kyrene; † um 194 v. Chr. in Alexandria) war ein außergewöhnlich vielseitiger griechischer Gelehrter in der Blütezeit der hellenistischen Wissenschaften.

Er betätigte sich als Mathematiker, Geograph, Astronom, Historiker, Philologe, Philosoph und Dichter. Im Auftrag der ägyptischen Könige aus der Dynastie der Ptolemäer leitete er rund ein halbes Jahrhundert lang die Bibliothek von Alexandria, die bedeutendste Bibliothek der Antike. Berühmt ist er vor allem als Begründer der wissenschaftlichen Geographie. Seine auf sorgfältigen Messungen beruhende Bestimmung des Erdumfangs gehört zu den bekanntesten wissenschaftlichen Leistungen des Altertums. Von seinen zahlreichen verlorenen Werken ist nur ein winziger Bruchteil aus Zitaten und Berichten späterer Autoren bekannt, was eine Würdigung seines Lebenswerks sehr erschwert. ↪ zum Artikel

Galileo Galilei

Galileo Galilei (* 15. Februar 1564 in Pisa; † 8. Januar 1642 in Arcetri bei Florenz) war ein italienischer Philosoph, Mathematiker, Physiker und Astronom, der bahnbrechende Entdeckungen auf mehreren Gebieten der Naturwissenschaften machte. In methodischer Hinsicht ist die streng mathematische, und zwar geometrische Vorgehensweise Galileis bemerkenswert. ↪ zum Artikel

Hypatia

Hypatia (auch Hypatia von Alexandria, griechisch Ὑπατία Hypatía; * um 355 in Alexandria; † März 415 oder März 416 in Alexandria) war eine griechische spätantike Mathematikerin, Astronomin und Philosophin. Von ihren Werken ist nichts erhalten geblieben, Einzelheiten ihrer Lehre sind nicht bekannt. Sie unterrichtete öffentlich und vertrat einen vermutlich mit kynischem Gedankengut angereicherten Neuplatonismus. Als Vertreterin einer nichtchristlichen philosophischen Tradition gehörte sie im überwiegend christlichen Alexandria der bedrängten paganen Minderheit an. Dennoch konnte sie lange unangefochten lehren und erfreute sich hohen Ansehens. Schließlich wurde sie aber das Opfer eines politischen Machtkampfs, in dem religiöse Gegensätze instrumentalisiert wurden. Eine aufgehetzte christliche Menge brachte sie in eine Kirche, ermordete sie dort und schändete den Leichnam. ↪ zum Artikel

Nikolaus von Kues

Nikolaus von Kues, latinisiert Nicolaus Cusanus oder Nicolaus de Cusa (* 1401 in Kues an der Mosel, heute Bernkastel-Kues; † 11. August 1464 in Todi, Umbrien), war ein berühmter, universal gebildeter deutscher Philosoph, Theologe und Mathematiker. Er gehörte zu den ersten deutschen Humanisten in der Epoche des Übergangs zwischen Spätmittelalter und Früher Neuzeit.

Das mathematische und naturwissenschaftliche Werk des Cusanus ist vor allem von seinem Interesse an Wissenschaftstheorie und von seinen metaphysisch-theologischen Fragestellungen geprägt; er will von mathematischen zu metaphysischen Einsichten hinführen. Mit dem Problem der Kreisquadratur und der Berechnung des Kreisumfangs setzt er sich in mehreren Schriften auseinander. Er hält eine Kreisquadratur nur näherungsweise für möglich und schlägt dafür ein Verfahren vor. ↪ zum Artikel

Mathias Metternich

Mathias Metternich (* 8. Mai 1747 in Steinefrenz, Kurfürstentum Trier; † 28. Oktober 1825 in Mainz, Großherzogtum Hessen) war Professor für Mathematik und Physik an der Kurfürstlichen Universität zu Mainz. Seine Studien, bei denen er zum Doktor der Philosophie promoviert wurde, betrieb er an der Kurfürstlichen Universität in Mainz und später an der Universität Göttingen, wo er unter anderem Student bei Abraham Gotthelf Kästner und Georg Christoph Lichtenberg war.

Trotz Metternichs zahlreich publizierter Werke als Mathematiker und Physiker wird in der Rezeption seines Lebenswerks vornehmlich seine Rolle als revolutionärer Politiker und Publizist während der 1780er und 1790er Jahre gewürdigt. ↪ zum Artikel

Florence Nightingale

Florence Nightingale (* 12. Mai 1820 in Florenz, Großherzogtum Toskana; † 13. August 1910 in London) war eine Begründerin der modernen westlichen Krankenpflege und einflussreiche Reformerin des Sanitätswesens und der Gesundheitsfürsorge in Großbritannien und Britisch-Indien. Sie trug wesentlich dazu bei, dass sich die Krankenpflege zu einem gesellschaftlich geachteten und anerkannten Berufsweg für Frauen entwickelte und legte Ausbildungsstandards fest, die zuerst in der von ihr gegründeten Krankenpflegeschule umgesetzt wurden.

Die mathematisch hoch begabte Nightingale gilt außerdem als Pionierin der visuellen Veranschaulichung von Zusammenhängen in der Statistik. ↪ zum Artikel

Alfred North Whitehead

Alfred North Whitehead (* 15. Februar 1861 in Ramsgate; † 30. Dezember 1947 in Cambridge (Massachusetts)) war ein britischer Philosoph und Mathematiker.

Bekannt wurde Alfred Whitehead durch das Standardwerk „Principia Mathematica“ über Logik, das er zusammen mit seinem langjährigen Schüler und Freund Bertrand Russell zwischen 1911 und 1913 in drei Bänden veröffentlichte. Es stellte den Versuch dar, im Sinne des logizistischen Programmes alle wahren mathematischen Aussagen und Beweise auf eine symbolische Logik zurückzuführen. Obwohl ein geplanter vierter Band nicht mehr veröffentlicht wurde und die Frage, ob der Versuch selbst erfolgreich war, weiterhin kontrovers diskutiert wird, wurde „Principia Mathematica“ zu einem der einflussreichsten Bücher der Geschichte der Mathematik und Logik. ↪ zum Artikel

Siehe auch

• Exzellenzinitiative Mathematik
• Weitere exzellente Artikel in der Wikipedia
• Exzellente Bilder und Grafiken zum Thema Mathematik