Polygonzug (Geodäsie)

Ein Polygonzug (A-B-C-D-E) zum Vermessen eines Straßenstücks. Der Exzenterpunkt Exz ist für die hinteren Hausecken erforderlich.

Ein Polygonzug ist die Spur eines Weges, der sich aus endlich vielen Geradenstücken zusammensetzt. In der Geodäsie und im Bauwesen sind Polygonzüge die wichtigsten Messlinien für terrestrische Detailvermessungen. Dort dienen Polygonzüge vor allem der Koordinatenbestimmung mehrerer Neupunkte in einem Arbeitsgang. Das Messen von Polygonzügen wird als Polygonierung bezeichnet.

Wortherkunft

Das Wort Polygon stammt von altgriechischen πολυγώνιον (polygṓnion ‚Vieleck‘) und rührt her von πολύς (polýs , ‚viel‘) und γωνία (gōnía, Winkel‘).^[1]

Prinzip der Polygonzugmessung

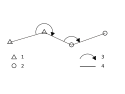
Ein Polygonzug hat folgende Elemente: die Polygonpunkte PP, die Polygonseiten ${\displaystyle {s_{i}}}$ und die Brechungswinkel ${\displaystyle {\beta _{i}}}$. Die Brechungswinkel werden mit einem Winkelmessinstrument (z. B. einem Theodolit), die Horizontalstrecken mit einem Längenmessgerät gemessen. Instrumente, die beides messen können, werden Tachymeter genannt. Aus den Brechungswinkeln und den Strecken werden die Koordinaten der einzelnen Polygonpunkte durch fortgesetztes polares Anhängen berechnet.

Die einzelnen Teilstrecken sind in der Regel – je nach Gelände, Bebauung oder geforderter Genauigkeit – etwa 50 bis 200 Meter lang. Die Polygonpunkte werden im Boden durch Pflöcke oder Metallstifte vermarkt, um sie auch für spätere Vermessungen oder fallweise Kontrollen nutzen zu können. Über den Bodenpunkten werden Stative mit dem Tachymeter bzw. den Zielzeichen (Prismenreflektoren) aufgestellt und exakt zentriert, so dass die genauen Brechungswinkel und Strecken gemessen werden können. Tachymeter und Prismen sind untereinander austauschbar ohne das Stativ zu verändern (Zwangszentrierung). Die Genauigkeit liegt im mm-Bereich.

Früher wurden Messtische oder Theodolit und Maßband verwendet; seit der flächendeckenden Einführung elektronischer Tachymeter ist dies überholt.

Polygonzugarten

In der Geodäsie unterscheidet man mehrere Arten von Polygonzügen:

Offene Polygonzüge

offener Polygonzug (3); 1 = bekannte Punkte, 2 = neu zu bestimmende Punkte, 3 = Brechungswinkel, 4 = Polygonseiten

beidseitig angeschlossener Polygonzug (4); 1 = bekannte Punkte, 2 = neu zu bestimmende Punkte, 3 = Brechungswinkel, 4 = Polygonseiten

1. Zug mit einseitigem Koordinaten- und Richtungsanschluss (d. h. der Startpunkt des Polygonzugs ist aus einer anderen Messung festgelegt, ebenso die Richtung zum zweiten Punkt), ohne Koordinaten- und Richtungsabschluss (kein festgelegter Endpunkt, z. B. aus einer anderen Messung, keine festgelegte Richtung vom vorletzten zum letzten Polygonzugspunkt)
2. Zug mit einseitigem Koordinaten- und zweiseitigem Richtungsanschluss
3. Zug mit einseitigem Koordinatenanschluss, ohne Fernziel für den Endpunkt (kein Richtungsabschluss)
4. Zug mit beidseitigem Richtungs- und Koordinatenanschluss (voll angeschlossener Zug)

Geschlossener Polygonzug

Ringpolygon; 1 = bekannte Punkte, 2 = neu zu bestimmende Punkte, 3 = Brechungswinkel, 4 = Polygonseiten

• Ringpolygon (Anfangs- und Endpunkt sind identisch)

Polygonnetze

Polygonnetz

Polygonnetze entstehen durch die Verknotung mehrerer Polygonzüge.

Anwendungsgebiete

Polygonzüge sind wichtige Messungslinien in der Geodäsie. Die Polygonpunkte dienen als Messpunkte, mit denen das Netz der amtlichen Festpunkte weiter verdichtet wird, indem zwischen deren bekannten Koordinaten die ${\displaystyle t_{i}}$ als Zwischenpunkte eingerechnet werden. Sie werden auch zur Vermessung von Gebäuden, von großen Maschinen und von Bergwerken verwendet (siehe Markscheidewesen). Polygonzüge dienen zur Bestimmung von Aufnahmepunkten für die Objektvermessung (z. B. Orthogonalwinkelaufnahme, Polaraufnahme, Grenzpunkte), sowie für topographische Vermessung (z. B. Polaraufnahme bei Geländepunkten) und Absteckungsaufgaben.

Anforderungen

Von den Neupunkten (Polygonpunkte) aus sollte möglichst viel vom aufzunehmenden Gebiet erfasst werden, die Polygonseiten sollten möglichst gestreckt und gleich lang sein. Zweckmäßigerweise werden die Neupunkte für Nachmessungen vermarkt.

Siehe auch

• Fehlerfortpflanzung
• Polygonzug (Mathematik)
• Richtungskontrolle mit Fernziel, Sonnenazimut oder Vermessungskreisel (Kreiselazimut)
• Netzausgleichung, Vermessungsnetz

Literatur

• Eberhard Baumann: Vermessungskunde. Bd. 2, Dümmler, Bonn 1995, ISBN 978-3-42-779056-3.
• Paul Knufinke: Allg. Vermessungs- und Markscheidekunde. Bochum 1990, ISBN 978-3-89-653530-6.
• Asbeck, Drüppel, Gärtner (Hrsg.), Skindelies, Stein: Vermessung und Geoinformation. 12. Auflage. Düsseldorf 2012, ISBN 978-3-00-038273-4, S. 161.

Weblinks

• Polygonzug. (PDF; 245 kB) Hochschule Bochum, abgerufen am 21. November 2013 (Skript zur Vermessungskunde). 
• Polygonzug. Abgerufen am 21. November 2013. 
• Polygonierung. (PDF; 177 kB) Abgerufen am 21. November 2013. 

Einzelnachweise

1. ↑ Wilhelm Gemoll: Griechisch-Deutsches Schul- und Handwörterbuch. G. Freytag Verlag/Hölder-Pichler-Tempsky, München/Wien 1965.