Polygoneffekt

Der Polygoneffekt tritt auf, wenn ein Zugmittel (Kette und Zahnriemen sind Zugmitteltriebe) durch ein Antriebsrad formschlüssig (d. h. durch Ineinandergreifen) eine Arbeitsmaschine antreibt.

Dabei kann das Zugmittel auf dem Antriebsrad nicht kreisrund auf- und ablaufen, sodass es zu Abwinkelungen des Zugmittels kommt. Dadurch entsteht aus dem kreisrunden Antriebsrad wirkmäßig ein Polygon (Vieleck) mit unterschiedlich vielen Sehnen entsprechend dem Durchmesser des Antriebsrades.

Definition und Auftreten

Dreht sich das Antriebsrad mit konstanter Winkelgeschwindigkeit, so kommt es durch die Polygonauflage des Zugmittels zu unterschiedlichen Wirkradien. Die Geschwindigkeit des Zugmittels schwankt dann periodisch um eine mittlere Geschwindigkeit. Des Weiteren resultieren daraus unangenehme Erregungen in Längs- und Querrichtung des Zugmittels, die zu Schwingungen führen können, welche im Extrem zur Resonanzkatastrophe und damit meist zum Materialbruch führen.

Aufgrund des Schwingungsphänomens durch den Polygoneffekt und der Übertragungsungenauigkeit gibt es in allen Bereichen des Maschinenbaues, in denen die Zugmittel Kette oder Zahnriemen verwendet werden, vereinfachte Berechnungen.

Speziell im Motorenbau wird für die Nockenwellensteuerung (mit Kette oder Zahnriemen) ein exaktes Übertragungsverhalten der Steuerkette verlangt, das aufwändig vorherberechnet werden kann.

Bei Positionieraufgaben mit zahnriemengetriebenen Fahrzeugen kann die Nichtberücksichtigung des Polygoneffekts zu Ungenauigkeiten führen.

Rundstahlkettentrieb im Kettenzug

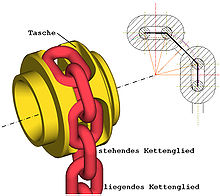
Der Polygoneffekt bei Stahlgelenkketten, z. B. im Kettengetriebe, unterscheidet sich von jenem bei Rundstahlketten, da letztere aus einer Abfolge von jeweils um 90° zueinander verdrehten Kettengliedern bestehen. Diese liegen unterschiedlich in der Kettennuss auf und bewirken dadurch veränderte geometrische Zusammenhänge: man unterscheidet stehende und liegende Kettenglieder. Die Kraft wird dabei von der hängenden Kette nur über die liegenden Glieder auf das Kettenrad übertragen.

Bei den Rundstahlketten haben die Antriebsräder geringe Zähne(Ecken)zahlen und somit die Polygone nur wenige Seiten. Dies bringt den Vorteil, dass die Antriebsmomente für das Kettenrad klein gehalten werden können und das Kettenrad mit Antrieb nicht viel Bauraum benötigt. Aber: je kleiner die Anzahl der Polygonseiten, desto größer die Auswirkungen des Polygoneffekts.

Kinematische Verhältnisse

Dreht sich ein Rundstahlkettenrad (vgl. Abbildung) mit konstanter Winkelgeschwindigkeit, dann entstehen folgende kinematische Verhältnisse:

Man erkennt, dass sich die Kinematik nach 90° wiederholt, also periodisch ist, weil das Kettenrad vier Taschen hat. Die zweimaligen Beschleunigungssprünge während einer Periode erregen die an der Kette hängenden Lasten zu Schwingungen in Kettenlängsrichtung, da die Rundstahlkette (elastisch) mit der hängenden Last vereinfacht einen Einmassenschwinger bildet. Diese erzwungene Schwingung führt zu unerwünschten Betriebszuständen.

Schwingung durch Polygoneffekt

Wird eine Last von 1600 kg mit einem 2,3 kW starken Kettenzug mit einer mittleren Hubgeschwindigkeit von 8 m/min angehoben und anschließend abgesenkt, entstehen an der Last die im Bild rechts gezeigten Beschleunigungen und entsprechende dynamische Kräfte.

Es wird erkennbar, dass zur Hublast von 15696 N (= 1600 kg • 9,81 m/s²) noch eine Zusatzkraft von 5280 N (= 1600 kg • 3,3 m/s²) die Kette beim Senken zusätzlich belastet. Dies tritt hier bei einer Kettenlänge von 10,3 m auf. Es werden jeweils nach dem Anfahren Resonanzen mit bis zur IV. Ordnung durchlaufen, die Frequenzen liegen dabei unter 10 Hz. Diese niederfrequenten Schwingungen sind mit freiem Auge zu beobachten und verursachen mitunter eine Amplitude von mehr als 40 mm.

Simulation der dynamischen Gesamtsituation

Wenn man die physikalischen Zusammenhänge mathematisch genau beschreibt und noch die Eigenschaften der Kette und des Kettenzuges sehr genau kennt – dies lässt sich experimentell ermitteln – kann man mittels numerischer Lösungsverfahren alle diese beschreibenden Gleichungen lösen, und das Verhalten der Last und des Kettenzuges vorherberechnen.

Dazu bedarf es unzähliger Rechenschritte des Simulations- oder Lösungsprogrammes mit entsprechend hohem Rechenzeitbedarf, von bis zu einigen Stunden. Das Ergebnis sollte dann aber, bei genügend genauer Modellbildung mit der gemessenen Wirklichkeit gut übereinstimmen.

Das Bild zeigt gute Übereinstimmung von Messung und Berechnung (Simulation) für einen polygoneffekterregten Hubvorgang. Weiters ist darin der Messaufbau mit Kettenzug, Kette, Kraftmessdose und Last abgebildet.

Literatur

• Christian Landschuetzer: Analyse von Schwingungen an einsträngigen Elektrokettenzügen. Diss. TU Graz, 2004.

Weblinks

• Theo Korse, Martin Sopouch: Eine neue Steuerkette ohne Polygoneffekt (theoretisch), erschienen in MTZ worldwide 5/2004, S. 382.