Peter Wason
Peter Cathcart Wason (* 22. April 1924 in Bath, England; † 17. April 2003 in Wallingford, England) war ein englischer Denkpsychologe.
Er gehörte zu den führenden Forschern der experimentellen Denkpsychologie. Mit seinen drei paradigmatischen Experimenten, der 2-4-6-Aufgabe, der Selection Task und der THOG-Aufgabe, setzte er eine bis heute anhaltende weltweite Forschungstätigkeit in Gang[1].
Leben
Wason entstammt einer fortschrittlich-liberalen, politisch aktiven Familie. Sein Urgroßvater Peter Rigby Wason und sein Großonkel Cathcart Wason waren beide Mitglieder des House of Commons.
Nach dem Krieg, den er als Verbindungsoffizier in der Normandie verbrachte, ging er zunächst ans New College (Oxford), um Englisch zu studieren. Nach kurzer Zeit als Dozent an der Universität Aberdeen entschloss er sich 1950, Psychologie am University College London zu studieren, wo er mehr als 30 Jahre blieb.
Peter Wason war ein Internationaler Meister im Fernschach. Er war zweimal verheiratet und hinterließ zwei Töchter.
Werk
Wason war einer der ersten, der mit experimentellen Mitteln untersuchte, welche systematischen Fehler beim Denken gemacht werden.
2-4-6-Aufgabe
Der Versuchsleiter hat sich eine Regel ausgedacht, die bestimmte Zahlentripel produziert (zum Beispiel: „drei beliebige Zahlen in aufsteigender Reihenfolge“). Eines dieser Tripel, z. B. 2-4-6, nennt er der Testperson. Deren Aufgabe besteht darin, die gedachte Regel durch Versuch und Irrtum herauszufinden. Dazu soll sie dem Versuchsleiter Zahlentripel nennen, der dann mit „Ja, dieses Tripel entspricht meiner Regel“ oder „Nein, dieses Tripel entspricht nicht meiner Regel“ antwortet. Die Testperson ist also auf Vermutungen angewiesen, sie wird daher Hypothesen aufstellen (z. B. „gerade Zahlen“) und dann testen. Es zeigte sich nun, dass die Mehrzahl der Testpersonen eine positive Teststrategie bevorzugt. Sie nennen also häufig Tripel wie „8-10-12“ und so weiter und bekommen auch immer ein „Ja“ dafür, ohne der Lösung näher zu kommen. Im vorliegenden Fall wäre eine falsifizierende Teststrategie sinnvoller, da die naheliegende Hypothese („gerade Zahlen in aufsteigender Reihenfolge“) enger gefasst ist als die tatsächliche Regel.[2] Eine die eigene Hypothese („gerade Zahlen in aufsteigender Reihenfolge“) falsifizierende Teststrategie könnte beinhalten: 1) „24-22-04“ (Falsifizierung „aufsteigende Reihenfolge“) und 2) „1-3-7“ (Falsifizierung „nur gerade Zahlen“). Im Falle eines „Nein“ für 1) und „Ja“ für 2) ist die Wahrscheinlichkeit, dass die Regel „drei beliebige Zahlen in aufsteigender Reihenfolge“ lautet hoch.
Die Eignung der 2-4-6-Aufgabe zum Nachweis einer aus dem Confirmation bias herrührenden Anwendung positiver Teststrategien der Teilnehmer ist in der Fachliteratur stark umstritten. Ryan D. Tweney gab in Untersuchungen getrennten Gruppen von Teilnehmern beispielsweise die Zusatzinformation zur Aufgabe, dass sie eine bestätigende bzw. widerlegende Teststrategie verfolgen sollten. Beide Gruppen hatten dieselbe Erfolgsquote zur Ermittlung der Regel. Es wurde daraus geschlossen, dass es keine Korrelation zwischen der Erfolgsquote des Tests und der Anwendung einer ausschließlich positiven Teststrategie gibt.[3]
Eine starke Reduktion der Anzahl von Versuchen zur Ermittlung der korrekten Regel sowie die Erhöhung der Gesamterfolgsquote beim Lösen konnte durch eine Abwandlung des Originaltests hin zu einer Kategorisierungsaufgabe nach Einführung der Regeln „DAX“ und „MED“ erreicht werden. Bei DAX handelt es sich um die Originalregel, während MED alle komplementären Regeln, d. h. jene die nicht durch DAX abgedeckt werden, beinhaltet. Diese Komplementarität war den Teilnehmern jedoch unbekannt und die Rückmeldung bestand nur in der Antwort: gehört zu „DAX“ bzw. gehört zu „MED“. Die Teilnehmer reagierten darauf mit einer höheren Variabilität an getesteten Zahlentriples im Vergleich zum Originaltest, der nur eine einzige Regel als Lösungziel beinhaltet. Das Ergebnis unterstreicht die Relevanz komplementärer Lösungsansätze zur Lösung von Aufgaben bei denen eine ausschließlich positive oder negative Teststrategie weniger erfolgreich ist.[4][5]
Selection Task
Vor dem Probanden liegen vier Karten. Sie zeigen E, K, 4, 7. Jede Karte hat einen Buchstaben auf der einen und eine Zahl auf der anderen Seite. Der Versuchsleiter behauptet: „Wenn auf der einen Seite der Karte ein Vokal ist, dann ist auf der anderen Seite eine gerade Zahl.“ Welche Karten muss die Testperson umdrehen, um die Regel zu überprüfen?
Fast alle Versuchspersonen überprüfen richtigerweise die „E“-Karte (Modus ponens), viele zusätzlich (falsch) die „4“-Karte, kaum jemand (was richtig wäre) die „7“-Karte (Modus tollens).[6][7]
Später haben andere Forscher gezeigt, dass die richtige Auswahl viel häufiger getroffen wird, wenn der Inhalt realistisch, das heißt weniger abstrakt, und/oder deontisch ist („Wer Alkohol trinken will, muss mindestens 18 Jahre alt sein“).[8]
THOG-Aufgabe
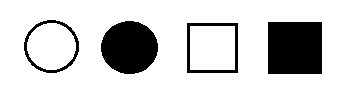
Vor dem Probanden liegen vier Karten. Sie zeigen:
- ein schwarzes Quadrat
- ein weißes Quadrat
- einen schwarzen Kreis
- einen weißen Kreis
Der Versuchsleiter sagt: „Ich habe mir eine Farbe (schwarz oder weiß) und eine Form (Quadrat oder Kreis) ausgesucht. Eine Karte, die genau eine dieser Eigenschaften hat, aber nicht beide, ist ein THOG. Das schwarze Quadrat ist ein THOG. Was kann man über die anderen drei Karten sagen (ist ein THOG / ist kein THOG / nicht entscheidbar)?“
Wie bei allen von Wasons Logikfragen ist es auch bei der THOG-Aufgabe unbedingt notwendig, dass die Fragestellung vom Versuchsleiter so genau und schlüssig wie möglich dargestellt wird, da die Schwierigkeit dieser Aufgabe dadurch entsteht, dass viele Informationen gleichzeitig bedacht werden müssen, was eine starke Belastung des Arbeitsgedächtnisses bedeutet.[9] Dies merkt man daran, dass viele Probanden, auch wenn die Frage genau gestellt wurde, sagen, dass der weiße Kreis kein THOG wäre, da er keine der Eigenschaften des schwarzen Quadrat besitzt. Über den schwarzen Kreis und das weiße Quadrat könne man keine Aussage treffen. Dies ist aber nicht richtig wenn wir alle gegebenen Information beachten.
Der richtige Lösungsweg wäre folgender:
Der Versuchsleiter kann sich eins dieser 4 Paare von Eigenschaften ausgesucht haben:
- schwarz und quadratisch
- schwarz und kreisförmig
- weiß und quadratisch
- weiß und kreisförmig
Wir wissen vom Versuchsleiter, dass das schwarze Quadrat ein THOG ist, weil es genau eine der ausgesuchten Eigenschaften hat. Die Eigenschaft, die es zu einem THOG macht, ist also entweder schwarz oder quadratisch – jedoch nicht beides. Der Versuchsleiter kann sich also nicht 1. schwarz und quadratisch ausgesucht haben, sonst wäre das schwarze Quadrat kein THOG. Auch kann er sich nicht 4. Weiß und kreisförmig ausgesucht haben, da sonst das schwarze Quadrat keine der ausgesuchten Eigenschaften besitzen würde und somit kein THOG wäre. Dies bedeutet, der Versuchsleiter hat sich entweder 2. Schwarz und kreisförmig oder 3. Weiß und quadratisch ausgesucht. Bei diesen beiden Paaren wäre der weiße Kreis jedenfalls ein THOG, da er entweder wie in 2. kreisförmig (aber nicht auch schwarz) oder wie in 3. weiß (aber nicht auch quadratisch) ist. Das weiße Quadrat und der schwarzen Kreis können also keine THOGs sein, da sie entweder beide oder keine der Eigenschaften aus den Paaren 2. und 3. besitzen würden.
Die Lösung lautet also: Der weiße Kreis ist ein THOG, die beiden anderen Karten sind keine THOGs.
Veröffentlichungen
- mit Philip Johnson-Laird: Thinking and Reasoning. Penguin Books, Harmondsworth 1968
- mit Philip Johnson-Laird: Psychology of Reasoning: Structure and Content. 1972; Taschenbuch: Harvard University Press, 1990, ISBN 0674721276
- mit Philip Johnson-Laird: Thinking: Readings in Cognitive Science. Cambridge University Press, 1977, ISBN 0521217563
- mit William Hartston: The Psychology of Chess. Facts on File, 1983, ISBN 0871962268
Literatur
- Stephen Newstead & Jonathan St. B. T. Evans (Hrsg.): Essays In Honour Of Peter Wason. Psychology Press, 1995, ISBN 978-0-86377-358-7
Weblinks
- Nachruf von Jonathan St B. T. Evans im Independent, 22. April 2003
- Nachruf von Philip Johnson-Laird im Guardian, 25. April 2003
- Nachruf im Daily Telegraph, 21. April 2003
- Peter Cathcart Wason auf der Website von Herbert Huber (mit veranschaulichten Problemstellungen)
Einzelnachweise
- ↑ Rüdiger F. Pohl (Hrsg.): Cognitive Illusions. A Handbook on Fallacies and Biases in Thinking, Judgement and Memory. Psychology Press, Hove and New York 2004, ISBN 978-1-84169-351-4.
- ↑ P. C. Wason: On the failure to eliminate hypotheses in a conceptual task. In: Quarterly Journal of Experimental Psychology. 12, 1960, S. 129–140
- ↑ Tweney, Ryan D., et al.: Strategies of rule discovery in an inference task. Quarterly Journal of Experimental Psychology, 32, Nr. 1, 1980, 109-123, doi:10.1080/00335558008248237.
- ↑ Maggie Gale, John Ball Linden: Does Positivity Bias Explain Patterns of Performance on Wason’s 2-4-6 Task?. Proceedings of the Twenty-Fourth Annual Conference of the Cognitive Science Society, 24(24), 2002, 340-344, doi:10.4324/9781315782379-95.
- ↑ Christine Hoffmann(2001). Dissertation. Hypothesentesten – Der Einfluß von Phänomenwahrscheinlichkeit und Informationsmenge auf den Schlußfolgerungsprozeß. Albert-Ludwigs-Universität zu Freiburg i. Br. S. 33
- ↑ P. C. Wason: Reasoning about a rule. In: Quarterly Journal of Experimental Psychology. 20, 1968, S. 273–281
- ↑ Wenn Sie dieses Rätsel lösen, haben Sie einen Gehirnschaden. In: NZZ Folio. 12/07.
- ↑ Wason Four Cards Test (Seite nicht mehr abrufbar, festgestellt im Dezember 2022. Suche in Webarchiven.) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis. (PDF; 28 kB). Referat für ein Seminar von Friedel Bolle, Website der Europa-Universität Viadrina
- ↑ P. C. Wason, P. G. Brooks: THOG: The anatomy of a problem. In: Psychological Research. 41. Jahrgang, Nr. 1, 1979, S. 79–90, doi:10.1007/BF00309425 (englisch, eurekamag.com [PDF]).
| Personendaten | |
|---|---|
| NAME | Wason, Peter |
| ALTERNATIVNAMEN | Wason, Peter Cathcart |
| KURZBESCHREIBUNG | englischer Denkpsychologe |
| GEBURTSDATUM | 22. April 1924 |
| GEBURTSORT | Bath, England |
| STERBEDATUM | 17. April 2003 |
| STERBEORT | Wallingford, England |