Perspektive Zuordnung

Perspektive Zuordnung ist ein Begriff aus der projektiven Geometrie und bezeichnet in einer projektiven Ebene eine besondere Beziehung zwischen eindimensionalen Grundgebilden, also einer Punktreihe (alle Punkte einer Gerade) oder einem Geradenbüschel (alle Geraden durch einen festen Punkt).

Im einfachsten Fall stellt die Projektion einer Punktreihe auf eine andere von einem Punkt aus eine perspektive Zuordnung zweier Punktreihen dar. Es kann aber auch ein Geradenbüschel einer Punktreihe zugeordnet werden. Perspektive Zuordnungen können unter hinreichenden Bedingungen zu Perspektivitäten (Kollineationen) der projektiven Ebene fortgesetzt werden.

Eine projektive Zuordnung zwischen zwei Grundgebilden ist die Hintereinanderausführung endlich vieler perspektiver Zuordnungen. Sind zwei Grundgebilde durch perspektive oder projektive Zuordnung einander zugeordnet, so sagt man auch, sie befinden sich in perspektiver Lage bzw. projektiver Lage.

Die Bedeutung perspektiver bzw. projektiver Zuordnungen zeigt sich im Hauptsatz der projektiven Geometrie und dem Satz von Steiner über die Erzeugung eines Kegelschnitts.

Punktreihe und Geradenbüschel in perspektiver Lage

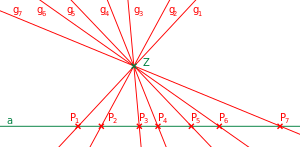
Die geometrisch einfachste perspektive Zuordnung von eindimensionalen Gebilden in einer projektiven Ebene ist die Zuordnung zwischen einer Punktreihe, das heißt der Punktmenge einer Geraden ${\displaystyle a}$ in der Ebene und einem Geradenbüschel der gleichen Ebene, das heißt der Menge der Geraden durch einen festen Punkt ${\displaystyle Z}$ der Ebene, der nicht mit ${\displaystyle a}$ inzidiert. Die Zuordnung lässt sich formal so definieren:

${\displaystyle \Delta (a,Z):a\ni P\mapsto (P+Z)\ni Z.}$

Das heißt: Jedem Punkt ${\displaystyle P}$ auf ${\displaystyle a}$ wird die Verbindungsgerade ${\displaystyle P+Z}$^[1] zugeordnet, vergleiche die Abbildung rechts oben. Die Zuordnung ${\displaystyle \Delta (a,Z)}$ ist allein aufgrund der Inzidenzaxiome für projektive Ebenen wohldefiniert und bijektiv. Damit zeigt sich:

1. In einer projektiven Ebene ist jede projektive Punktreihe ${\displaystyle (a,\{a\},I_{a})}$ als Inzidenzstruktur^[2] isomorph zu der Inzidenzstruktur, die durch die Büschelstruktur ${\displaystyle (\{g|g\mathop {I^{-1}} Z\},\{Z\},(I^{-1})_{Z})}$ gegeben ist, sofern ${\displaystyle Z}$ nicht auf ${\displaystyle a}$ liegt. Dass diese letzte Bedingung fortgelassen werden kann, sieht man durch mehrmaliges perspektives Zuordnen.
2. Daraus ergibt sich: In jeder projektiven Ebene sind alle Punktreihen inzidenzisomorph zueinander und zu allen Geradenbüscheln. Insbesondere sind die „Punktmengen“ dieser Strukturen gleichmächtig.
3. Das bedeutet konkret für endliche Ebenen: Jede Gerade enthält gleich viele Punkte ${\displaystyle v_{1}=q+1}$, jedes Büschel gleich viele Geraden ${\displaystyle b_{1}=q+1}$ und es ist ${\displaystyle v_{1}=b_{1}}$. Das heißt: Jede endliche Ebene ist ein symmetrischer ${\displaystyle 2-(q^{2}+q+1,q+1,1)}$-Blockplan.^[3] Die Zahl ${\displaystyle q}$ ist hier die Ordnung der endlichen Ebene.
4. In jeder papposschen Ebene existiert eine Korrelation der Ebene ${\displaystyle ({\mathcal {P}},{\mathcal {G}},I)}$ in ihre (im Sinne der Inzidenzstruktur) duale Ebene ${\displaystyle ({\mathcal {G}},{\mathcal {P}},I^{-1})}$, die die Zuordnung ${\displaystyle \Delta (a,Z)}$ fortsetzt.
5. In jeder desarguesschen projektiven Ebene lässt sich durch die Zuordnung ein auf einer Punktreihe definiertes Doppelverhältnis auf Punktbüschel übertragen und umgekehrt.^[4]
6. In jeder angeordneten Ebene lässt sich die Anordnung einer Punktreihe durch die Zuordnung auf ein Punktbüschel übertragen und umgekehrt.^[4]
7. In jeder topologischen projektiven Ebene sind Punktbüschel und Punktreihen homöomorph.^[4]

Zwei Punktreihen in perspektiver Lage

Wenn man eine perspektive Zuordnung der Punktreihe auf einer Geraden ${\displaystyle a}$ auf das Punktbüschel der Geraden durch einen Punkt ${\displaystyle Z}$ mit einer solchen vom gleichen Punktbüschel auf die Punktreihe einer anderen Geraden ${\displaystyle b}$ zusammensetzt, dann erhält man eine perspektive Zuordnung zwischen den Punktreihen von ${\displaystyle a}$ und ${\displaystyle b}$. Voraussetzung ist, dass das gemeinsame Zentrum auf keiner der beiden Geraden ${\displaystyle a,b}$ liegt:

${\displaystyle \pi =\pi (a,Z,b):=\left(\Delta (b,Z)\right)^{-1}\circ \Delta (a,Z)}$

Man kann diese Zuordnung auch selbständig definieren:

${\displaystyle \pi (a,Z,b)(A)=B:\Leftrightarrow \left(A\in a\land B=(A+Z)\cap b\right)}$

Einem Punkt ${\displaystyle A\in a}$ wird also der Schnittpunkt der Verbindungsgeraden ${\displaystyle A+Z}$^[1] mit der Geraden ${\displaystyle b}$ zugeordnet. Die zweite Definition ist vorzuziehen, weil die zentralperspektive Zuordnung vom Punkt ${\displaystyle Z}$ aus abbildungstheoretisch einfacher (keine Dualität!) ist und sich unter schwächeren Bedingungen fortsetzen lässt:

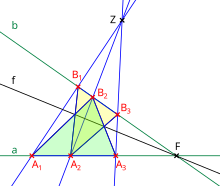
• In einer desarguesschen Ebene existiert wenigstens eine Projektivität, die ${\displaystyle \pi =\pi (a,Z,b)}$ fortsetzt. Sie kann als Perspektivität mit dem Zentrum ${\displaystyle Z}$ gewählt werden und ihre Achse kann, falls die Ebene auch noch dem Fano-Axiom genügt, aus zwei verschiedenen Punkt-Bildpunktpaare ${\displaystyle (A_{1},\pi (A_{1})),(A_{2},\pi (A_{2}))}$ konstruiert werden, wenn darunter nicht der Schnittpunkt ${\displaystyle F=a\cap b}$ ist, der durch ${\displaystyle \pi }$ sich selbst zugeordnet wird ${\displaystyle \left(\pi (F)=F\right)}$, vergleiche auch die Abbildung rechts: Das (einzig mögliche) Zentrum für die Perspektivität ergibt sich als Schnittpunkt der zwei Spuren ${\displaystyle Z=(A_{1}+B_{1})\cap (A_{2}+B_{2})}$. Einen Fixpunkt ${\displaystyle F}$, also einen Punkt auf der Achse ${\displaystyle f}$ bestimmt man als Schnittpunkt der Urbildgeraden ${\displaystyle a=A_{1}+A_{2}}$ mit ihrer Bildgeraden ${\displaystyle b=B_{1}+B_{2}}$, also ${\displaystyle F=a\cap b}$.

Aus zwei Punkt-Bildpunkt-Paaren ergibt sich ein zweiter Punkt der Achse, indem man sie, wie in der Abbildung gezeigt, „kreuzweise“ verbindet (die Strecken ${\displaystyle A_{1}B_{2}}$ usw. in der Abbildung). Beachte dazu, dass die farblich hervorgehobenen Dreiecke von ${\displaystyle Z}$ aus zentral-perspektiv liegen und dass ${\displaystyle f}$ die nach dem desarguesschen Satz existierende Achse für diese Konfiguration ist: Die Schnittpunkte zugeordneter Dreiecksseiten sind gerade die zwei im Bild gezeigten „Kreuzschnittpunkte“ und der oben beschriebene Fixpunkt ${\displaystyle F}$.^[5]

• In einer beliebigen projektiven Ebene ${\displaystyle \mathbb {P} }$ ist ${\displaystyle \pi (a,Z,b)}$ zu einer Kollineation der Gesamtebene fortsetzbar, wenn ${\displaystyle Z}$ in der Lenz-Barlotti-Figur ${\displaystyle {\mathcal {B}}(\mathbb {P} )}$ der Ebene zu einem Paar ${\displaystyle (c,Z)\in {\mathcal {B}}(\mathbb {P} )}$ mit ${\displaystyle c\not \in \{a,b\}}$ gehört. Die Kollineation braucht nicht eindeutig bestimmt zu sein, es gibt aber dann, falls die Ebene das Fano-Axiom erfüllt, auch eine Projektivität, die die Zuordnung fortsetzt, eine Perspektivität mit Zentrum ${\displaystyle Z}$.

Man kann die (zentral-)perspektive Zuordnung zwischen zwei projektiven Geraden auch affin spezialisieren: Ist ${\displaystyle Z}$ ein Fernpunkt, dann induziert ${\displaystyle \pi }$ auf den affinen Teilmengen der Punktreihen von ${\displaystyle a,b}$ eine bijektive Parallelprojektion. Diese Parallelprojektionen spielen in der synthetischen affinen Geometrie eine ähnlich zentrale Rolle, wie die Perspektivitäten in der projektiven.

Notation^[6]

Die Tatsache, dass eine geordnete Menge von kollinearen Punkten ${\displaystyle (A_{1},A_{2},\ldots )}$ perspektiv zu einer gleichartigen geordneten Menge liegt, kann man zur Definition einer Relation auf der Menge ${\displaystyle T}$ aller ${\displaystyle n}$-Tupel ${\displaystyle \left(n\in \mathbb {N} ,\,n\geq 2\right)}$ von kollinearen Punkten ${\displaystyle T:=\bigcup _{n=2}^{\infty }T_{n};T_{n}:=\{(A_{1},A_{2},\ldots A_{n})|\exists g\in {\mathcal {G}}:A_{1},A_{2},\ldots A_{n}\in g\}}$ verwenden. Diese Relation wird (im Beispiel der Abbildung rechts oben) als

${\displaystyle (A_{1},A_{2},A_{3})\doublebarwedge (B_{1},B_{2},B_{3});\quad (A_{1},A_{2},A_{3},F)\doublebarwedge (B_{1},B_{2},B_{3},F)}$ usw. notiert

oder auch genauer, mit dem vermittelnden Zentrum über dem Relationensymbol als

${\displaystyle (A_{1},A_{2},A_{3}){\stackrel {Z}{\doublebarwedge }}(B_{1},B_{2},B_{3});\quad (A_{1},A_{2},A_{3},F){\stackrel {Z}{\doublebarwedge }}(B_{1},B_{2},B_{3},F)}$

notiert. Gilt dann etwa mit (nicht unbedingt verschiedenen) Zentren ${\displaystyle Y,Z:\,\left[(A_{1},A_{2},A_{3}){\stackrel {Y}{\doublebarwedge }}(B_{1},B_{2},B_{3})\right]\land \left[(B_{1},B_{2},B_{3}){\stackrel {Z}{\doublebarwedge }}(C_{1},C_{2},C_{3})\right]}$, dann schreibt man ${\displaystyle (A_{1},A_{2},A_{3})\barwedge (C_{1},C_{2},C_{3})}$. Wenn man diese Relation entsprechend transitiv fortsetzt (über endlich viele^[7] statt nur zwei vermittelnde Zentren) dann ist die Relation ${\displaystyle \barwedge }$ in ${\displaystyle T}$ und in jeder Teilmenge ${\displaystyle T_{n}\subset T}$ eine Äquivalenzrelation. Man sagt dann von den Punkten ${\displaystyle (A_{1},A_{2},A_{3});(C_{1},C_{2},C_{3})}$ sie sind aufeinander projektiv bezogen oder auch sie liegen zueinander projektiv. Man beachte:

1. Für die perspektive Lage zueinander (Relation ${\displaystyle \doublebarwedge }$) und die projektive Lage (Relation ${\displaystyle \barwedge }$) zueinander von Punkten kommt es auf die Reihenfolge beider Punktmengen an! Die hier verwendete Tupelschreibweise, die dies formal absichert, wird in der Literatur meistens nicht (konsequent)^[8] verwendet.
2. Es muss im Allgemeinen für zwei ${\displaystyle n}$-Tupel, die perspektiv oder projektiv aufeinander bezogen sind, keine Kollineation existieren, die das eine Tupel auf das andere abbildet! Existiert eine solche Kollineation, dann existiert aber auch eine Projektivität mit dieser Eigenschaft. Dies ist für projektiv aufeinander bezogene ${\displaystyle n}$-Tupel über einer desarguesschen Ebene immer der Fall, und über jeder Ebene trivialerweise, wenn die beiden Tupel identisch sind. Jedes Tupel aus ${\displaystyle T}$ liegt offenbar projektiv zu sich selbst, meist wird vereinbart,^[9] dass ein solches Tupel sogar perspektiv zu sich selbst liegen soll, das vermittelnde Zentrum außerhalb der Trägergeraden ist dann beliebig. Da die Identität eine Projektivität ist, existiert mit ihr auch eine fortsetzende Kollineation, dies kann aber höchstens für eine Ebene der Lenz-Barlotti-Klasse I.1 die einzige Fortsetzung sein.
3. Die hier erläuterte moderne Notation für Sprechweisen des 19. Jahrhunderts ist durch die Sprache der modernen Mengenlehre im Grunde ein überflüssiger Formalismus: Die durch ${\displaystyle \pi =\pi (a,Z,b)}$ gegebene bijektive Abbildung ist selbst eine Relation, man kann die Punktreihe von ${\displaystyle a}$ selbst als Zählmenge verwenden, wobei man sie, falls nötig, mit einer Wohlordnung ausstattet, und damit jede beliebige, auch unendliche Teilmenge der Punktreihe von ${\displaystyle b}$ korrekt „nummerieren“. Für die einander projektiv zugeordneten Punktreihen, die also in der ${\displaystyle \barwedge }$-Relation zueinander stehen, gilt das Gleiche.

Zwei Geradenbüschel in perspektiver Lage

Dual zur perspektiven Zuordnung zweier Punktreihen von einem Zentrum aus ist die perspektive Lage zweier Geradenbüschel (mit den Punkten ${\displaystyle Y,Z}$ als Trägern) von einer Achse ${\displaystyle a}$ aus definiert. Die Achse darf in keinem der zugeordneten Büschel liegen, darf also keinen der Punkte ${\displaystyle Y,Z}$ enthalten.

${\displaystyle \Pi (Y,a,Z):=\Delta (a,Z)\circ \left(\Delta (a,Y)\right)^{-1}}$

Selbständige Definition:

${\displaystyle \Pi (Y,a,Z)(g)=(g\cap a)+Z;\;\left(Y\in g\right)}$^[1]

Für diese (axial-)perspektive Zuordnung ${\displaystyle \Pi (Y,a,Z)}$ des Geradenbüschels durch ${\displaystyle Y}$ zu dem Geradenbüschel durch ${\displaystyle Z}$von der Achse ${\displaystyle a}$ aus gelten die zu den Aussagen des vorigen Absatzes dualen Aussagen.

Die Relations-Notation (Relation ${\displaystyle {\stackrel {a}{\doublebarwedge }}}$) und eine transitive Fortsetzung (Relation ${\displaystyle \barwedge }$) zwischen ${\displaystyle n}$-Tupeln von Geraden aus je einem Punktbüschel wird analog zu der oben für Punkttupel beschriebenen vereinbart, die Sprechweisen sind ebenfalls analog: Tripel mit ${\displaystyle (g_{1},g_{2},g_{3}){\stackrel {a}{\doublebarwedge }}(h_{1},h_{2},h_{3})}$ liegen (von der Achse ${\displaystyle a}$ aus) perspektiv zueinander, sind also auch projektiv aufeinander bezogen ${\displaystyle \left((g_{1},g_{2},g_{3})\barwedge (h_{1},h_{2},h_{3})\right)}$ usw.

Punktreihe und Kegelschnitt oder Oval in perspektiver Lage

Die Abbildung rechts zeigt einen Kreis ${\displaystyle k}$ und eine Gerade ${\displaystyle a}$, deren Punktmengen vom Zentrum ${\displaystyle Z}$ aus, das auf der Kreislinie liegt, zueinander perspektiv liegen. Die Zuordnung ${\displaystyle \pi =\pi (a,Z,k)}$ ordnet jedem Punkt ${\displaystyle P}$ der Punktreihe den Schnittpunkt aus ${\displaystyle (P+Z)\cap k}$ (in der projektiv abgeschlossenen Ebene) zu, der von ${\displaystyle Z}$ verschieden ist, es sei denn, diese Schnittmenge enthält nur ${\displaystyle Z}$, dann dieses Zentrum ${\displaystyle Z}$. Die Verbindungsgeraden, die die Zuordnung vermitteln, sind in der Abbildung durch blaue Halbgeraden dargestellt. Die „Verbindungsgerade ${\displaystyle t:=Z+Z}$“ ist hier die Tangente an ${\displaystyle k}$ im Punkt ${\displaystyle Z}$, denn diese Tangente hat einen „doppelt zählenden“ Schnittpunkt mit ${\displaystyle k}$. Diese Gerade trifft bei dieser Wahl von ${\displaystyle a}$ diese Gerade in deren Fernpunkt, im Bild angedeutet durch zwei Pfeile.

Weiter oben wurde bereits erläutert, dass die Abbildung ${\displaystyle \Delta (a,Z)}$ die Punktreihe bijektiv der Menge der Büschelgeraden zuordnet. Die Antworten auf die folgenden drei Fragen der so dargestellten Relation zwischen Punkten einer Kreislinie (allgemeiner: Punkten auf einem nichtausgearteten Kegelschnitt ${\displaystyle {\mathcal {Q}}}$) besagen, dass es sich um eine bijektive Funktion handelt (die Injektivität ist dann trivialerweise gegeben):^[10]

1. Schneidet jede Gerade durch ${\displaystyle Z}$ außer der Tangente in ${\displaystyle Z}$ den Kegelschnitt den Kegelschnitt noch einmal, ist also ${\displaystyle \pi }$ für jeden Punkt definierbar?
2. Ist die Abbildung eindeutig definierbar oder kann es Geraden ${\displaystyle P+Z}$ geben, die ${\displaystyle k}$ mehr als zweimal treffen?
3. Ist die Abbildung surjektiv, wird also jeder Punkt auf der Kreislinie von einer Geraden getroffen?

Begründungen^[10]

1. Würde eine Gerade ${\displaystyle P_{0}+Z}$ den Kegelschnitt in keinem weiteren Punkt außer in ${\displaystyle Z}$ schneiden, dann wäre auch diese Gerade eine Tangente im Punkt ${\displaystyle Z}$. Dies tritt aber aus rein rechnerischen Gründen (nichtausgearteter Kegelschnitt!) nur einmal beim Einsetzen der linearen Geradengleichungen in die quadratische Gleichung auf. Im Bild dann, wenn ${\displaystyle P_{0}}$ der Fernpunkt von ${\displaystyle a}$ ist.^[11]
2. Geraden ${\displaystyle P+Z}$ die den Kegelschnitt mehr als zweimal treffen, kann es nicht geben, sonst wäre der Kegelschnitt ausgeartet.
3. Ein nichtgetroffener Punkt ${\displaystyle Q\neq Z}$ hat aber doch eine Verbindungsgerade mit dem Zentrum, diese schneidet aber ${\displaystyle a}$, also wird ${\displaystyle Q}$ doch getroffen.

Folgerungen

Für ein Oval ${\displaystyle {\mathcal {Q}}}$ in einer papposschen Ebene, die dem Fano-Axiom genügt, ist die perspektive Zuordnung von einem Zentrum ${\displaystyle Z\in {\mathcal {Q}}}$ auf eine Gerade ${\displaystyle a\not \ni Z}$ ebenfalls eine bijektive, perspektive Zuordnung, genau so sind die Ovale definiert.^[10] Daher gelten die nachfolgenden Aussagen sowohl für jede Quadrik ${\displaystyle {\mathcal {Q}}}$ als auch für jedes Oval ${\displaystyle {\mathcal {Q}}}$ in einer solchen Ebene:

• Die Frage der Fortsetzbarkeit stellt sich für die Zuordnung ${\displaystyle \pi =\pi (a,Z,{\mathcal {Q}})}$ so nicht, da kollineare auf nichtkollineare Punkte bezogen werden.
• Ist die Ebene endlich, dann enthält ${\displaystyle {\mathcal {Q}}}$ genau ${\displaystyle q+1}$ Elemente, wobei ${\displaystyle q}$ die Ordnung der Ebene ist.
• Auf ${\displaystyle {\mathcal {Q}}}$ lassen sich (auf verschiedene Arten, je nach Wahl von ${\displaystyle Z,a}$) eindimensionale Koordinaten einführen, wodurch diese Kurve zu einem eindimensionalen projektiven Raum über dem Koordinatenkörper der Ebene wird.
• Eine Anordnung der projektiven Ebene induziert eine eindeutige Anordnung auf jedem Kreis und umgekehrt.
• In einer topologischen projektiven Ebene ist ${\displaystyle {\mathcal {Q}}}$ homöomorph zu jeder projektiven Geraden. Speziell: Eine Gerade in einer topologischen projektiven Ebene ist ein topologischer Kreis.

Projektive Zuordnungen und der Hauptsatz der projektiven Geometrie

• Eine projektive Zuordnung ist eine Verkettung von perspektiven Zuordnungen (s. o.) zwischen den Punktreihen von zwei verschiedenen projektiven Geraden.

Die folgende Aussage wurde in der Geometrie der Lage des 19. Jahrhunderts als Hauptsatz der projektiven Geometrie^[12] bezeichnet:

Eine Projektivität ist bestimmt, wenn drei Punkte einer Geraden und die entsprechenden drei der anderen Geraden gegeben sind.^[13]

Bei dieser Formulierung des Satzes ist zu beachten:

1. „Projektivität“ bezeichnet hier eine projektive Zuordnung, und nicht eine projektive Kollineation der gesamten Ebene oder gar des Raumes! Über die Existenz oder Eindeutigkeit einer solchen Fortsetzung wird hier nichts ausgesagt.
2. Im Zusammenhang wird vorausgesetzt, dass beide projektiven Geraden in einer gemeinsamen Ebene liegen, also gleichwertig einander schneiden. Auch die verketteten perspektiven Zuordnungen können dann ganz in dieser Ebene vorgenommen werden.
3. Die Entsprechung des Satzes („entsprechende Punkte“) ist in modernerer Formulierung eine Relation zwischen Punktetripeln, also zwischen geordneten Mengen von drei (für diesen Satz verschiedenen) Punkten. Anders formuliert: Es ist für den Satz wichtig, welcher der drei Punkte auf der ersten Geraden, welchem auf der zweiten „entspricht“.

Eine moderne Formulierung, die diese drei zu beachtenden Bedingungen berücksichtigt, lautet:^[14]

Axiom P7′: Es seien ${\displaystyle a,b}$ verschiedene Geraden in einer projektiven Ebene. Es seien ${\displaystyle A_{1},A_{2},A_{3}\in a;B_{1},B_{2},B_{3}\in b}$ jeweils Tripel verschiedener Punkte.^[15] Dann existiert genau eine projektive Zuordnung ${\displaystyle \pi :a\rightarrow b}$, so dass ${\displaystyle (A_{1},A_{2},A_{3})\barwedge (B_{1},B_{2},B_{3})}$ bezüglich dieser projektiven Zuordnung gilt, vergleiche dazu auch die erste Abbildung rechts.

Die folgenden Varianten des Hauptsatzes sind zueinander äquivalente Aussagen über eine projektive Ebene und gleichwertig zum Satz von Pappos (PA):^[16]

• Axiom P7′
• Axiom P7: Es seien ${\displaystyle a}$ eine Gerade in einer projektiven Ebene. Es seien ${\displaystyle (A_{1},A_{2},A_{3}),(B_{1},B_{2},B_{3})}$ zwei Tripel aus drei unterschiedlichen Punkten auf ${\displaystyle a}$. Dann existiert höchstens eine projektive Zuordnung ${\displaystyle \pi :a\rightarrow a}$, bezüglich der ${\displaystyle (A_{1},A_{2},A_{3})\barwedge (B_{1},B_{2},B_{3})}$ gilt.
• Axiom P7″: Es seien ${\displaystyle a,b}$ verschiedene Geraden in einer projektiven Ebene, ${\displaystyle F=a\cap b}$ ihr Schnittpunkt. Dann ist jede projektive Zuordnung ${\displaystyle \pi :a\rightarrow b}$, die ${\displaystyle F}$ fixiert (das heißt mit ${\displaystyle \pi (F)=F}$) eine perspektive Zuordnung.

Für jede projektive Ebene sind die drei genannten P7-Aussagen äquivalent zu den dualisierten Aussagen. Als Beispiel die duale Form von P7:^[14]

D7: Es sei ${\displaystyle Z}$ ein Punkt in einer projektiven Ebene. Es seien ${\displaystyle (g_{1},g_{2},g_{3}),(h_{1},h_{2},h_{3})}$ zwei Tripel aus drei unterschiedlichen Geraden durch ${\displaystyle Z}$. Dann existiert höchstens eine projektive Zuordnung ${\displaystyle \Pi :\{g|g\ni Z\}\rightarrow \{g|g\ni Z\}}$, bezüglich der ${\displaystyle (g_{1},g_{2},g_{3})\barwedge (h_{1},h_{2},h_{3})}$ gilt.

Literatur

• Arrigo Bonisoli: On collineation groups of finite planes. Socrates Intensive Programme, Dipartimento di Matematic a Università della Basilicata, Potenza, Italien (ugent.be [PDF; abgerufen am 8. Januar 2012] Wie der Titel schon sagt: Gruppenstruktur der Kollineationsgruppe). 
• Harold Scott MacDonald Coxeter: Reelle projektive Geometrie der Ebene. Nach der 2. engl. Auflage übersetzt von W. Burau. Hrsg.: Wilhelm Blaschke (= Mathematische Einzelschriften. Band 3). 1. deutsche Auflage. R. Oldenbourg, München 1955 (Das Lehrbuch bringt die klassische, reelle „Geometrie der Lage“ des 19. Jahrhunderts in relativ moderner Formulierung, vor allem erläutert der Autor bzw. Übersetzer ausführlich, auf wen bestimmte Ideen und Sprechweisen zurückgehen und der Übersetzer erläutert Unterschiede zwischen deutschem und amerikanischem Sprachgebrauch). 
• Hans Walser: Projektive Abbildungen, zeichnerischer Zugang. Eidgenössische Technische Hochschule, Zürich (ethz.ch [PDF; abgerufen am 8. Januar 2012] Vorlesungsskript; Zahlreiche Abbildungen, die aber großteils zu Übungsaufgaben gehören und daher (nach Anleitungen im Text) zu vervollständigen sind). 
• Erich Hartmann: Projektive Geometrie. Technische Universität, Darmstadt 2006 (mathematik.tu-darmstadt.de [PDF; abgerufen am 8. Januar 2012] Kurzskript). 
• Lars Kadison, Matthias T. Kromann: Projective Geometry and Modern Algebra. Birkhäuser, Boston / Basel / Berlin 1996, ISBN 3-7643-3900-4 (Konsequenzen des Fano-Axioms und der Sätze von Desargues und Pappos für die Transitivitätseigenschaften der projektiven Gruppen). 
• Albrecht Beutelspacher, Ute Rosenbaum: Projektive Geometrie. Von den Grundlagen bis zu den Anwendungen (= Vieweg Studium: Aufbaukurs Mathematik). 2., durchgesehene und erweiterte Auflage. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X. 
• Günter Pickert: Projektive Ebenen. 2. Auflage. Springer, Berlin / Heidelberg / New York 1975, ISBN 3-540-07280-2 (Anwendung der Perspektivitäten vor allem in nichtdesarguesschen Ebenen). 

Hauptsatz der projektiven Geometrie

• Harold Scott MacDonald Coxeter: Reelle projektive Geometrie der Ebene. Nach der 2. engl. Auflage übersetzt von W. Burau. Hrsg.: Wilhelm Blaschke (= Mathematische Einzelschriften. Band 3). 1. deutsche Auflage. R. Oldenbourg, München 1955 (Das Lehrbuch bringt die klassische, reelle „Geometrie der Lage“ des 19. Jahrhunderts in relativ moderner Formulierung, vor allem erläutert der Autor bzw. Übersetzer ausführlich, auf wen bestimmte Ideen und Sprechweisen zurückgehen und der Übersetzer erläutert Unterschiede zwischen deutschem und amerikanischem Sprachgebrauch). 
• Karl Georg Christian von Staudt: Geometrie der Lage. 1857, § 110, S. 52 (Formulierung und Beweis des Hauptsatzes der projektiven Geometrie für den reellen Fall). 

Einzelnachweise und Anmerkungen

1. ↑ ^{a b c} Das Pluszeichen zwischen Punkten wird hier nach Pickert (1975) so verstanden, dass die Summe der Punkte deren Verbindungsgerade darstellt. Im desarguesschen Fall handelt es sich im Standardmodell tatsächlich um die Summe zweier Unterräume eines (Links-)Vektorraums.
2. ↑ ${\displaystyle I_{a}}$ bezeichnet die auf die Punktreihe von ${\displaystyle a}$ eingeschränkte Inzidenzrelation.
3. ↑ Für die Parameter ${\displaystyle t=2,v_{0}=q^{2}+q+1}$ in der Bezeichnung ${\displaystyle t-(v_{0},v_{1},b_{2})}$ wendet man für ${\displaystyle t=2,b_{2}=1}$ das Inzidenzaxiom an: Zwei Geraden schneiden sich in genau einem Punkt. Für die Gesamtpunktzahl ${\displaystyle v_{0}}$ zählt man von einem Punkt ${\displaystyle P_{0}}$ aus alle Punkte auf allen Büschelgeraden durch ${\displaystyle P_{0}}$. Diese Zahl ist ${\displaystyle b_{1}\cdot v_{1}-q=(q+1)^{2}-q}$. Dabei hat man ${\displaystyle P_{0}}$ selbst zunächst mehrfach, nämlich ${\displaystyle (q+1)}$-mal gezählt und zieht deshalb ${\displaystyle q}$ von dem Produkt ab. Beutelspacher und Rosenbaum (2004)
4. ↑ ^{a b c} Dafür ist es nicht notwendig, dass sich die perspektive Zuordnung zu einer Korrelation der gesamten Ebene auf ihre duale Ebene fortsetzen lässt.
5. ↑ Betrachtet man zwei Kreuzschnittkonfigurationen und die Dreiecke isoliert, dann hat man auch eine Pappuskonfiguration, aber dadurch, dass die Tripel perspektiv zueinander liegen, greift der desarguessche Satz. Kadison und Kromann (1996), chapter 6:The Fundamental theorem for perspectivities on a line
6. ↑ Nach Coxeter (1955) S. 27. Die Notation geht laut Coxeter auf Veblen und Young: Projective Geometry. Band I. Boston 1910.  zurück.
7. ↑ In beliebigen Ebenen genügen, wenn es über endlich viele Zentren möglich ist, dafür bereits höchstens 4 vermittelnde Zentren, in desarguesschen Ebenen drei, wenn die Punktetupel auf der gleichen Gerade liegen, sonst zwei. Pickert (1975)
8. ↑ Etwa auch bei Coxeter (1955)!
9. ↑ Coxeter (1955), S. 28.
10. ↑ ^{a b c} Beutelsbacher, Rosenbaum (2004), Kapitel 4: Quadratische Mengen.
11. ↑ Die Wahl des Zentrums auf der Kreislinie ist für dieses Argument wesentlich: Die zu lösende quadratische Gleichung hat im Koordinatenkörper ${\displaystyle K}$ (pappossche Ebene) dadurch eine Lösung und damit (unter Voraussetzung des Fano-Axioms, womit ${\displaystyle \operatorname {char} (K)\neq 2}$ gilt) auch noch eine zweite, die entweder doppelt-zählend gleich oder von der ersten verschieden ist.
12. ↑ von Staudt (1857)
13. ↑ Bezeichnung und Formulierung des Satzes wörtlich aus Coxeter (1955), 4: Satz des Pappos, 4.2: Der Hauptsatz der projektiven Geometrie.
14. ↑ ^{a b} Übersetzt aus Kadison und Kromann (1996): 6.1: The Fundamental theorem: Axiom P7.
15. ↑ Auch der Schnittpunkt ${\displaystyle S=a\cap b}$ darf in einem oder beiden Tripeln vorkommen! Kadison und Kromann (1996): 6.1: The Fundamental theorem: Axiom P7
16. ↑ Übersetzt aus Kadison und Kromann (1996): 6.1: The Fundamental theorem: Axiom P7.