Permutationsmatrix

Eine Permutationsmatrix oder auch Vertauschungsmatrix ist in der Mathematik eine Matrix, bei der in jeder Zeile und in jeder Spalte genau ein Eintrag eins ist und alle anderen Einträge null sind. Jede Permutationsmatrix entspricht genau einer Permutation einer endlichen Menge von Zahlen. Wird eine Permutationsmatrix mit einem Vektor multipliziert, dann werden die Komponenten des Vektors entsprechend dieser Permutation vertauscht. Permutationsmatrizen sind orthogonal, doppelt-stochastisch und ganzzahlig unimodular. Die Menge der Permutationsmatrizen fester Größe bildet mit der Matrizenmultiplikation eine Untergruppe der allgemeinen linearen Gruppe. Permutationsmatrizen werden unter anderem in der linearen Algebra, der Kombinatorik und der Kryptographie verwendet.
Definition
Eine Permutationsmatrix ist eine quadratische Matrix, bei der genau ein Eintrag pro Zeile und Spalte gleich ist und alle anderen Einträge gleich sind.[1] Hierbei sind im Allgemeinen und das Einselement und Nullelement eines zugrunde liegenden Rings (in der Praxis meist die reellen Zahlen). Jede Permutationsmatrix der Größe entspricht genau einer Permutation der Zahlen von bis . Die zu einer Permutation zugehörige Permutationsmatrix
hat dann als Einträge
wobei das Kronecker-Delta bezeichne. Werden durch die Permutation genau zwei Zahlen miteinander vertauscht, so bezeichnet man auch als Vertauschungsmatrix. Ist der -te kanonische Einheitsvektor als Zeilenvektor, dann lässt sich die Permutationsmatrix auch durch
darstellen. Gelegentlich findet sich allerdings in der Literatur auch die umgekehrte Variante, bei der die Einheitsvektoren spaltenweise zusammengesetzt werden, wodurch die Permutationsmatrizen entsprechend transponiert werden.[2] Im Folgenden wird jedoch die gebräuchlichere erste Variante verwendet.
Beispiel
Die zu der Permutation
zugehörige Permutationsmatrix ist
- .
Nachdem durch die Permutation beispielsweise die Zahl auf die Zahl abgebildet wird, findet sich in der fünften Zeile von die in der dritten Spalte.
Anwendung
Wird eine Permutationsmatrix mit einem gegebenen Spaltenvektor multipliziert, dann ergibt das Matrix-Vektor-Produkt
einen neuen Spaltenvektor, dessen Einträge entsprechend der Permutation vertauscht wurden. Ist beispielsweise , dann ergibt das Matrix-Vektor-Produkt mit der obigen Beispiel-Permutationsmatrix den Spaltenvektor
Wird eine Matrix von links mit einer Permutationsmatrix multipliziert, dann werden die Zeilen der Matrix gemäß der Permutation vertauscht. Umgekehrt ergibt die Multiplikation eines Zeilenvektors mit der transponierten Permutationsmatrix wieder einen Zeilenvektor mit entsprechend der Permutation vertauschten Elementen, also
- .
Für obiges Beispiel erhält man somit
Wird eine Matrix von rechts mit der transponierten Permutationsmatrix multipliziert, werden entsprechend die Spalten der Matrix gemäß der Permutation vertauscht.
Eigenschaften


Inverse
Permutationsmatrizen sind stets invertierbar, wobei die Inverse einer Permutationsmatrix gerade ihre Transponierte ist. Die transponierte Matrix ist dabei die Permutationsmatrix der inversen Permutation, es gilt also
- .
Reelle Permutationsmatrizen sind demnach stets orthogonal und haben vollen Rang .
Produkt
Das Produkt zweier Permutationsmatrizen ist wieder eine Permutationsmatrix, die der Hintereinanderausführung der zugehörigen Permutationen entspricht. Die Permutationsmatrix der Hintereinanderausführung zweier Permutationen ergibt sich zu
- .
Die Abbildung stellt somit einen Antihomomorphismus dar. Die Menge der Permutationsmatrizen bildet zusammen mit der Matrizenmultiplikation eine Gruppe, und zwar eine Untergruppe der allgemeinen linearen Gruppe . Jede Permutationsmatrix kann dabei als Produkt von elementaren zeilenvertauschenden Matrizen dargestellt werden.
Potenzen
Ganzzahlige Potenzen von Permutationsmatrizen sind wieder Permutationsmatrizen. Für jede Permutationsmatrix gibt es dabei eine Potenz , sodass
ergibt, wobei die Einheitsmatrix ist. Das kleinste positive mit dieser Eigenschaft ist gleich der Ordnung von in der allgemeinen linearen Gruppe. Diese Ordnung ist gleich dem kleinsten gemeinsamen Vielfachen der Längen der disjunkten Zyklen von .
Determinante
Die Determinante einer Permutationsmatrix ist entweder oder und entspricht dem Vorzeichen der zugehörigen Permutation:
- .
Eine Permutationsmatrix über den ganzen Zahlen ist damit eine ganzzahlige unimodulare Matrix. Die Spur einer ganzzahligen Permutationsmatrix entspricht der Anzahl der Fixpunkte der Permutation.
Die Determinante kann mit dem folgenden Schema ermittelt werden. Dazu wird für jede Spalte der Matrix die Zeilennummer, in der die eins steht, nebeneinander in eine Tabelle geschrieben. Darunter wird für jede Zahl z der ersten Zeile die Anzahl der Zahlen geschrieben, die größer als z sind und in der Tabelle links von z stehen; diese Anzahl heißt Kennmarke. Bei der eingangs angegebenen 8×8-Permutationsmatrix ergibt sich
| Zeilennummer z | 4 | 7 | 1 | 6 | 2 | 8 | 5 | 3 |
|---|---|---|---|---|---|---|---|---|
| Kennmarke a | 0 | 0 | 2 | 1 | 3 | 0 | 3 | 5 |
Ist die Summe der Kennmarken, wie hier, eine gerade Zahl, dann ist die Determinante 1, sonst −1; als Formel bei einer Permutationsmatrix der Größe :[3]
- mit
Eigenwerte
Die Eigenwerte einer reellen Permutationsmatrix sind nicht notwendigerweise alle reell, sie liegen aber auf dem komplexen Einheitskreis. Sind die Längen der Zyklen einer Permutation , dann sind die Eigenwerte der zugehörigen Permutationsmatrix die komplexen Einheitswurzeln
für und . Eine reelle Permutationsmatrix besitzt demnach genau dann den Eigenwert , wobei und teilerfremd seien, wenn die zugrunde liegende Permutation mindestens einen Zyklus aufweist, dessen Länge durch teilbar ist. Die Vielfachheit dieses Eigenwerts entspricht dann der Anzahl solcher Zyklen. Eine reelle Permutationsmatrix besitzt daher stets den Eigenwert mit Vielfachheit gleich der Gesamtzahl der Zyklen der zugrunde liegenden Permutation.
Normen
Da reelle Permutationsmatrizen orthogonal sind, gilt für ihre Spektralnorm
- .
Für die Spalten- und Zeilensummennorm einer reellen Permutationsmatrix ergibt sich ebenfalls
- .
Eine reelle Permutationsmatrix ist damit eine doppelt-stochastische Matrix. Nach dem Satz von Birkhoff und von Neumann ist eine quadratische Matrix genau dann doppelt-stochastisch, wenn sie eine Konvexkombination von Permutationsmatrizen ist.
Spezialfälle
- Die Permutationsmatrix der identischen Permutation ist die Einheitsmatrix.
- Eine Permutationsmatrix ist genau dann symmetrisch, wenn die zugrunde liegende Permutation selbstinvers ist.
- Weist eine Permutationsmatrix eine Blockstruktur auf, dann lässt sich die zugrunde liegende Permutation als Summe von Permutationen darstellen.
Verwendung
| a | b | c | d | e | f | g | h | ||
| 8 | 8 | ||||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h |
Acht sich wechselseitig nicht angreifende Türme auf einem Schachbrett
Permutationsmatrizen werden unter anderem verwendet:
- in der linearen Algebra als Elementarmatrizen bei der Gauß-Elimination zur Lösung linearer Gleichungssysteme
- in der Kombinatorik bei der Matrixdarstellung von Permutationsgruppen
- in der Kryptographie als Komponenten von Blockverschlüsselungsverfahren
In der Schachmathematik bilden die Permutationsmatrizen gerade die Lösungen des Problems, Türme auf ein Schachbrett der Größe so zu verteilen, dass sich keine Türme gegenseitig angreifen. Schwieriger zu lösen ist das Damenproblem, bei dem die Türme durch Damen ersetzt werden, die auch diagonal angreifen können. Die Lösungen des Damenproblems sind ebenfalls Permutationsmatrizen.
Verallgemeinerung
Eine verallgemeinerte Permutationsmatrix oder monomiale Matrix ist eine quadratische Matrix , bei der genau ein Eintrag pro Zeile und Spalte ungleich ist. Monomiale Matrizen haben die Darstellung
- ,
wobei eine gewöhnliche Permutationsmatrix und eine Diagonalmatrix ist, deren Diagonaleinträge alle ungleich sind. Die regulären monomialen Matrizen bilden mit der Matrizenmultiplikation als Verknüpfung die monomiale Gruppe , eine weitere Untergruppe der allgemeinen linearen Gruppe . Spezielle monomiale Matrizen sind vorzeichenbehaftete Permutationsmatrizen, bei denen in jeder Zeile und jeder Spalte genau ein Eintrag oder ist und alle übrigen Einträge sind.
Siehe auch
- Rothe-Diagramm
- Irreduzible Matrix
- Levi-Civita-Symbol
- Zyklische Matrix
Literatur
- Siegfried Bosch: Lineare Algebra. Springer, 2006, ISBN 3-540-29884-3.
- Jörg Liesen, Volker Mehrmann: Lineare Algebra. 3. Auflage. Springer, Berlin, Heidelberg 2021, ISBN 978-3-662-62741-9, doi:10.1007/978-3-662-62742-6.
Einzelnachweise
- ↑ Jörg Liesen, Volker Mehrmann: Lineare Algebra. Springer, 2011, S. 45.
- ↑ Siegfried Bosch: Lineare Algebra. Springer, 2006, S. 275.
- ↑ R. Zurmühl, S. Falk: Matrizen und ihre Anwendungen 1. Grundlagen, Für Ingenieure, Physiker und Angewandte Mathematiker. Springer, Berlin u. a. 1997, ISBN 3-540-61436-2, S. 57.
Weblinks
- Eric W. Weisstein: Permutation Matrix. In: MathWorld (englisch).
- Wkbj79: Permutation Matrix. In: PlanetMath. (englisch)
Auf dieser Seite verwendete Medien
Blank 45x45 square for use in chess templates (2nd version
Autor/Urheber: Cburnett, Lizenz: CC BY-SA 3.0
Light rook on transparent square, default size 45x45
Autor/Urheber: ManiacParisien, Lizenz: CC BY-SA 3.0
A Costas array composed of non-attacking kings
Autor/Urheber:
| Watchduck You can name the author as "T. Piesk", "Tilman Piesk" or "Watchduck". |


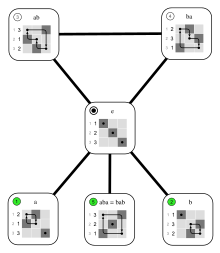
Cayley table of the 6 permutations of 3 elements, represented by matrices
|
|

(These matrices form the same group.)
| This SVG was created with Inkscape. |
Positions of the entries 0 ... 5 in the Cayley table of S3:
|
|