Pentachoron
| Regelmäßiges Pentachoron (5-Zeller) | |
|---|---|
 Schlegeldiagramm (Ecken und Kanten) | |
| Typ | Regelmäßiges Polychoron |
| Familie | Simplex |
| Zellen | 5 (3.3.3) |
| Flächen | 10 {3} |
| Kanten | 10 |
| Ecken | 5 |
| Eckfigur | (3.3.3) |
| Schläfli-Symbol | {3,3,3} |
| Coxeter-Dynkin-Diagramm | |
| Symmetriegruppe | A4, [3,3,3] |
| Eigenschaften | konvex |

Ein Pentachōron (das, von altgriechisch πεντα-penta-, Präfixform von πέντεpénte ‚fünf‘, und χῶροςchōros ‚Raum‘; auch 5-Zeller, Pentatop, vierdimensionale Hyperpyramide oder vierdimensionales Hypertetraeder genannt) ist eine vierdimensionale Hyperpyramide mit einem Tetraeder als „Grundfläche“, bzw. ein 4-Simplex, das einfachste Polychoron (vierdimensionale Figur). Es besteht aus fünf tetraederförmigen Zellen und ist das Analogon zum Dreieck (2-Simplex) und zum Tetraeder (3-Simplex).
Das regelmäßige Pentachoron ist eines der sechs regelmäßigen, konvexen Polychora (der sechs Platonischen Körper im 4-dimensionalen Raum) und wird vom Schläfli-Symbol {3,3,3} repräsentiert.
Geometrie
Ein Pentachoron besteht aus fünf Zellen, die alle tetraederförmig sind. Seine Eckfigur ist ein Tetraeder. Seine maximale Durchschneidung mit dem dreidimensionalen Raum ist das Dreiecksprisma.
Bilder
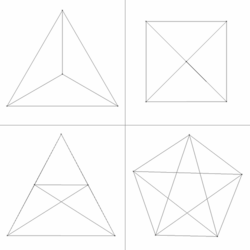
 Eine 3D-Projektion eines 5-Zellers, der eine Doppelrotation um zwei orthogonale Ebenen ausführt. | 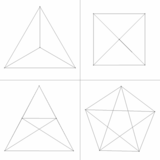 Vier orthographische Projektionen. |
Konstruktion
Ein Pentachoron kann konstruiert werden, indem zu einem Tetraeder eine fünfte Ecke hinzugefügt wird, die die gleiche Entfernung von den anderen Ecken hat wie die anderen Ecken untereinander (Im Wesentlichen ist ein Pentachoron eine vierdimensionale Pyramide mit einer tetraederförmigen Basis).
Projektionen
Eine mögliche Projektion des Pentachorons ist ein Pentagramm innerhalb eines Pentagons.
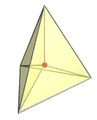
Die Ecke-Zuerst- und die Zelle-Zuerst-Parallelprojektion des Pentachorons in drei Dimensionen haben eine tetraederförmige Hülle. Das nächste bzw. die entfernteste Zelle wird auf den Tetraeder selbst projiziert, während die anderen vier Zellen auf die vier gestauchten tetraederförmigen Regionen, die das Zentrum umgeben, abgebildet werden.
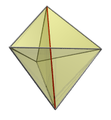
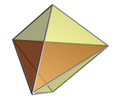
Die Kante-Zuerst- und die Fläche-Zuerst-Projektion des Pentachorons in drei Dimensionen haben eine doppeldreieckspyramidenförmige Hülle. Zwei der Zellen werden auf die obere und untere Hälfte der Doppelpyramide projiziert, während die übrigen drei auf drei nicht-regelmäßige tetraederförmige Körper um die zentrale Achse der Doppelpyramide mit Winkeln von jeweils 120° zueinander projiziert werden.
- Projektionen in den 3-dimensionalen Raum
- Ecke-Zuerst-Projektion
- Kante-Zuerst-Projektion
- Fläche-Zuerst-Projektion
- Zelle-Zuerst-Projektion
Formeln
| Größen eines Tesserakt mit Kantenlänge a | |
|---|---|
| Vierdimensionales Hypervolumen | |
| Begrenzungsvolumen | |
| Umkugelradius | |
| Kantenkugelradius | |
| Inkugelradius | |
Weblinks
- Platonische Polychora
- Eric W. Weisstein: Regular Polychoron. In: MathWorld (englisch).
Auf dieser Seite verwendete Medien
Four symmetry views of the 5-cell polytope, edges drawn with an orthographic projection (z-w axes ignored). Tiny squares are draw marking vertex positions. Some views have overlapping edges.
(c) Tetracube at en.wikipedia, CC BY 3.0
Cell-first projection of the 5-cell into 3D, hidden cells culled.
(c) Tetracube at en.wikipedia, CC BY 3.0
Vertex-first perspective projection of the pentachoron into 3D. The nearest vertex to the 4D viewpoint is shown, projecting to the center of the image.
Autor/Urheber: Der ursprünglich hochladende Benutzer war Tomruen in der Wikipedia auf Englisch, Lizenz: CC BY-SA 3.0
en:5-cell wireframe

|
Der Urheberrechtsinhaber dieser Datei, Robert Webb, erlaubt es jedem, diese für jeden Zweck zu benutzen, vorausgesetzt, dass der Urheberrechtsinhaber ordnungsgemäß genannt wird. Weiterverbreitung, Abänderungen, kommerzielle Nutzung sowie jede andere Verwendung sind gestattet. |
Namensnennung:
Attribution must be given to Robert Webb's Stella software as the creator of this image along with a link to the website: http://www.software3d.com/Stella.php. A complimentary copy of any book or poster using images from the Software would also be appreciated where feasible.
|
(c) Tetracube in der Wikipedia auf Englisch, CC BY 3.0
Edge-first projection of the pentachoron (5-cell) into 3D, with nearest edge shown.
Created by Jason Hise with Maya and Macromedia Fireworks.
A 3D projection of a 5-cell performing a simple rotation.Autor/Urheber: Tomruen, Lizenz: CC BY-SA 3.0
Elément graphique pour le diagramme de Coxeter-Dynkin avec les nombres entiers
(c) Tetracube at en.wikipedia, CC BY 3.0
Face-first projection of the 5-cell into 3D, with nearest face highlighted.
Autor/Urheber: Tomruen, Lizenz: CC BY-SA 3.0
Elément graphique pour le diagramme de Coxeter-Dynkin avec les nombres entiers
Autor/Urheber:

|
Eine Rastergrafik-Version dieses Bildes liegt vor. Diese sollte verwendet werden, wenn sie eine bessere Qualität aufweist.
File:Tetrahedron.svg → File:Tetrahedron.jpg
Weitere Informationen über Bildformate gibt es u.a. auf Commons:Dateitypen. |