Pellsche Gleichung

Als Pellsche Gleichung (nach John Pell, 1611–1685) bezeichnet man eine diophantische Gleichung der Form

${\displaystyle x^{2}-n\cdot y^{2}=1}$

mit positiv ganzzahligem ${\displaystyle n}$.

Ist ${\displaystyle n}$ eine Quadratzahl, so besitzt die Gleichung offenbar nur die trivialen Lösungen ${\displaystyle (\pm 1,\ 0)}$. Andernfalls gibt es unendlich viele Lösungen, die man mit Hilfe der Kettenbruchentwicklung von ${\displaystyle {\sqrt {n}}}$ bestimmen kann. Die verwandten Gleichungen ${\displaystyle x^{2}-n\cdot y^{2}=-1\,\!}$ und ${\displaystyle x^{2}-n\cdot y^{2}=\pm 4\;\!}$ werden oft ebenfalls Pellsche Gleichungen genannt.

Die Gleichung wird John Pell fälschlicherweise zugeschrieben. Korrekter wäre die Bezeichnung Fermatsche Gleichung.^[1][2]

Die Gleichung war schon Brahmagupta und Bhaskara II. bekannt. Die Lösung dieser Gleichung war als Problem von Pierre de Fermat in einem Brief an Bernard Frénicle de Bessy gestellt worden und 1657 als Problem veröffentlicht. Pell befasste sich nie mit der Lösung der Gleichung. Brouncker fand einige Lösungen (veröffentlicht im Commercium epistolicum of John Wallis 1658). Leonhard Euler stieß auf die Lösung von Brouncker in der lateinischen Ausgabe des Treatise of Algebra von John Wallis und benannte die Gleichung fälschlich nach Pell.^[3][4] Euler veröffentlichte zuerst 1732 über die Pell-Gleichung und fand später die Verbindung mit Kettenbrüchen (veröffentlicht 1765), die im Grunde schon hinter der Lösung von Brouncker steckt. Joseph-Louis Lagrange befasste sich nach Euler ausführlich mit der Gleichung und gab als Erster einen Beweis, dass es für jedes ${\displaystyle n}$ eine Lösung gibt, wobei Fermat möglicherweise auch einen Beweis hatte.^[5]

Das Auffinden aller Lösungen ist für spezielle ${\displaystyle n}$ äquivalent dazu, die Einheiten des Ganzheitsrings des reellquadratischen Zahlkörpers ${\displaystyle \mathbb {Q} ({\sqrt {n}})}$ zu finden. Nach dem Dirichletschen Einheitensatz hat die Einheitengruppe den Rang 1, d. h., es gibt eine Fundamentaleinheit (oder auch Grundeinheit) ${\displaystyle \varepsilon =x_{0}+y_{0}{\sqrt {n}},}$ mit der sich alle Lösungen als ${\displaystyle \pm \varepsilon ^{k},k\in \mathbb {N} }$ darstellen lassen.

Beispielsweise ist für ${\displaystyle n=2}$ die Einheit ${\displaystyle 1+1{\sqrt {2}}}$ eine Fundamentaleinheit und man kann die anderen Lösungen

${\displaystyle 3+2{\sqrt {2}},\ 7+5{\sqrt {2}},\ 17+12{\sqrt {2}},\ \ldots ,\ (1+1{\sqrt {2}})^{k}}$

aus ihr erzeugen.

Die Kettenbruchentwicklung einer quadratisch irrationalen Zahl ${\displaystyle {\sqrt {n}}}$ ist unendlich und periodisch. ${\displaystyle {\sqrt {n}}}$ hat die Kettenbruchentwicklung ${\displaystyle {\sqrt {n}}=[b_{0};\ {\overline {b_{1},\dotsc ,b_{m}}}]}$ (siehe Periodische Kettenbrüche). Sei

${\displaystyle {\frac {x}{y}}=[b_{0};\ b_{1},\dotsc ,b_{m-1}]}$

mit ganzzahligen ${\displaystyle x,\ y}$, dann ist ${\displaystyle x,\ y}$ die kleinste Lösung der verallgemeinerten Pellschen Gleichung ${\displaystyle x^{2}-n\cdot y^{2}={(-1)}^{m}}$. Die anderen Lösungen lassen sich wie erwähnt daraus konstruieren.^[6] Auch alle weiteren

${\displaystyle {\frac {x_{k}}{y_{k}}}=[b_{0};\ b_{1},\dotsc ,b_{km-1}]}$

mit ${\displaystyle k\in \mathbb {N} }$ lösen ${\displaystyle x^{2}-n\cdot y^{2}={(-1)}^{km}}$.

Die negative Pellsche Gleichung ${\displaystyle x^{2}-n\cdot y^{2}=-1}$ hat genau dann eine Lösung, wenn die Kettenbruchentwicklung von ${\displaystyle {\sqrt {n}}}$ eine ungerade Periode hat. Eine notwendige, aber nicht hinreichende Bedingung dafür ist, dass ${\displaystyle n}$ die Summe von zwei Quadratzahlen ist.^[7]

Das ist für 1, 2, 5, 10, 13, 17, 26, 29, 37, 41, 50, 53, 58, 61, 65, 73, 74, 82, 85, 89, 97, ... der Fall (siehe Folge A031396 in OEIS).

${\displaystyle {\sqrt {13}}}$ hat die Kettenbruchentwicklung

${\displaystyle {\sqrt {13}}=[3;\ {\overline {1,1,1,1,6}}]}$

Bricht man die Entwicklung jeweils an der Stelle ${\displaystyle k}$ ab, so erhält man beginnend mit ${\displaystyle k=1}$

${\displaystyle {\sqrt {13}}\approx {\frac {3}{1}},{\frac {4}{1}},{\frac {7}{2}},{\frac {11}{3}},{\frac {18}{5}}_{k=5},{\frac {119}{33}},{\frac {137}{38}},{\frac {256}{71}},{\frac {393}{109}},{\frac {649}{180}}_{k=10},{\frac {4287}{1189}},\ \dots }$

und findet an den Stellen ${\displaystyle k=5}$ und ${\displaystyle k=10}$ die Lösungen

${\displaystyle x_{0}=\ \ 18,\ y_{0}=\quad 5}$  von  ${\displaystyle x^{2}-13\cdot y^{2}=-1}$  und

${\displaystyle x_{1}=649,\ y_{1}=180}$  von  ${\displaystyle x^{2}-13\cdot y^{2}=+1}$.

Weiter stellt man fest, dass für ${\displaystyle n=13}$ jedes Element der abgebrochenen Kettenbruchentwicklung der Länge ${\displaystyle k=5l,\ l\in \mathbb {N} }$ eine Lösung einer Pellschen Gleichung mit rechter Seite ${\displaystyle \pm 1}$ ist, die Näherungsbrüche dazwischen lösen die Gleichung mit ${\displaystyle \pm 3}$ und ${\displaystyle \pm 4}$.

Ist eine Lösung ${\displaystyle (x_{0},\ y_{0})}$ bekannt, so lassen sich weitere Lösungen daraus bestimmen. Es gelten die rekursiven Gleichungen

${\displaystyle x_{i+1}=x_{0}\cdot x_{i}+n\cdot y_{0}\cdot y_{i}}$

${\displaystyle y_{i+1}=y_{0}\cdot x_{i}+x_{0}\cdot y_{i}}$

Dies ergibt sich aus dem Koeffizientenvergleich aus der Gleichung ${\displaystyle x+y\cdot {\sqrt {n}}=(x_{0}+y_{0}\cdot {\sqrt {n}})^{i}}$.

Das kann auch mit einer Matrizenmultiplikation dargestellt werden. Es gilt

${\displaystyle {\begin{pmatrix}x_{i+1}\\y_{i+1}\\\end{pmatrix}}={\begin{pmatrix}x_{0}&n\cdot y_{0}\\y_{0}&x_{0}\\\end{pmatrix}}\cdot {\begin{pmatrix}x_{i}\\y_{i}\\\end{pmatrix}}}$

Auf diese Weise können aus der kleinsten Lösung alle weiteren Lösungen bestimmt werden.^[8]

Die Lösungen können auch mit folgenden expliziten Formeln berechnet werden:^[9]

${\displaystyle x_{i}={\frac {1}{2}}\cdot \left((x_{0}+y_{0}\cdot {\sqrt {n}})^{i}+(x_{0}-y_{0}\cdot {\sqrt {n}})^{i}\right)}$

${\displaystyle y_{i}={\frac {1}{2\cdot {\sqrt {n}}}}\cdot \left((x_{0}+y_{0}\cdot {\sqrt {n}})^{i}-(x_{0}-y_{0}\cdot {\sqrt {n}})^{i}\right)}$

Die Pellsche Gleichung für ${\displaystyle n=3}$ hat die kleinste Lösung ${\displaystyle (x_{0}=2,\ y_{0}=1)}$. Die nächsten drei Lösungen berechnen sich dann wie folgt:

${\displaystyle {\begin{pmatrix}x_{1}\\y_{1}\\\end{pmatrix}}={\begin{pmatrix}2&3\\1&2\\\end{pmatrix}}\cdot {\begin{pmatrix}2\\1\\\end{pmatrix}}={\begin{pmatrix}7\\4\\\end{pmatrix}}}$

${\displaystyle {\begin{pmatrix}x_{2}\\y_{2}\\\end{pmatrix}}={\begin{pmatrix}2&3\\1&2\\\end{pmatrix}}\cdot {\begin{pmatrix}7\\4\\\end{pmatrix}}={\begin{pmatrix}26\\15\\\end{pmatrix}}}$

${\displaystyle {\begin{pmatrix}x_{3}\\y_{3}\\\end{pmatrix}}={\begin{pmatrix}2&3\\1&2\\\end{pmatrix}}\cdot {\begin{pmatrix}26\\15\\\end{pmatrix}}={\begin{pmatrix}97\\56\\\end{pmatrix}}}$

Für spezielle ${\displaystyle n}$ lässt sich die kleinste Lösung von ${\displaystyle x^{2}-n\cdot y^{2}=1}$ auf einfache Weise explizit bestimmen. Im Folgenden sei ${\displaystyle a}$ eine ganze Zahl mit ${\displaystyle a\geq 2}$.

• ${\displaystyle n=a^{2}-1}$: ${\displaystyle (x_{0}=a,\ y_{0}=1)}$
• ${\displaystyle n=a^{2}-2}$: ${\displaystyle (x_{0}=a^{2}-1,\ y_{0}=a)}$
• ${\displaystyle n=a^{2}+1}$: ${\displaystyle (x_{0}=2\cdot a^{2}+1,\ y_{0}=2\cdot a)}$
• ${\displaystyle n=a^{2}+2}$: ${\displaystyle (x_{0}=a^{2}+1,\ y_{0}=a)}$
• ${\displaystyle n=a\cdot (a+1)}$: ${\displaystyle (x_{0}=2\cdot a+1,\ y_{0}=2)}$

Außerdem ergeben sich für folgende ${\displaystyle n}$ die kleinsten Lösungen

• ${\displaystyle n=(a\cdot b)^{2}-b}$: ${\displaystyle (x_{0}=2\cdot a^{2}\cdot b-1,\ y_{0}=2\cdot a)}$ für ${\displaystyle b\geq 2}$
• ${\displaystyle n=(a\cdot b)^{2}-2\cdot b}$: ${\displaystyle (x_{0}=a^{2}\cdot b-1,\ y_{0}=a)}$
• ${\displaystyle n=(a\cdot b)^{2}+b}$: ${\displaystyle (x_{0}=2\cdot a^{2}\cdot b+1,\ y_{0}=2\cdot a)}$
• ${\displaystyle n=(a\cdot b)^{2}+2\cdot b}$: ${\displaystyle (x_{0}=a^{2}\cdot b+1,\ y_{0}=a)}$

Das sind Verallgemeinerungen der oben genannten Lösungsformeln.

Hier eine Tabelle der kleinsten Lösungen (Fundamentaleinheiten) von ${\displaystyle x^{2}-n\cdot y^{2}=1}$ mit ${\displaystyle 1\leq n\leq 128}$. Ist ${\displaystyle n}$ ein Quadrat gibt es nur die trivialen Lösungen ${\displaystyle (\pm 1,\ 0)}$.

Die Werte von ${\displaystyle x}$ und ${\displaystyle y}$ bilden die Folgen A002350^[10] und A002349^[11] in OEIS.

Eine verallgemeinerte Pellsche Gleichung ist eine diophantische Gleichung der Form

${\displaystyle x^{2}-d\cdot y^{2}=n}$

wobei ${\displaystyle d}$ eine positive ganze Zahl, aber keine Quadratzahl und ${\displaystyle n}$ eine ganze Zahl ungleich 0 ist. Um diese Gleichung vollständig zu lösen, muss als vorbereitender Schritt eine Lösung ${\displaystyle (x_{0},y_{0})}$ dieser Gleichung und außerdem die kleinste Lösung ${\displaystyle (p,q)}$ der entsprechenden (normierten) Pellschen Gleichung ${\displaystyle x^{2}-d\cdot y^{2}=1}$ bekannt sein. Dann kann man unendlich viele weitere Lösungen ${\displaystyle (x_{i},y_{i})}$ von ${\displaystyle x^{2}-d\cdot y^{2}=n}$ darstellen als

${\displaystyle x_{i}+y_{i}\cdot {\sqrt {d}}=(x_{0}+y_{0}\cdot {\sqrt {d}})\cdot (p+q\cdot {\sqrt {d}})^{i}}$

Es gelten also die rekursiven Gleichungen

${\displaystyle x_{i+1}=p\cdot x_{i}+d\cdot q\cdot y_{i}}$

${\displaystyle y_{i+1}=q\cdot x_{i}+p\cdot y_{i}}$

Für ${\displaystyle n\neq 1}$ kann es sein, dass die verallgemeinerte Pellsche Gleichung keine Lösungen besitzt, im Gegensatz zum schon betrachteten Fall ${\displaystyle n=1}$. Dies lässt sich oft mithilfe der Division mit Rest beweisen.

Um alle Lösungen der verallgemeinerten Pellsche Gleichung zu bestimmen, reicht es, endlich viele Lösungen ${\displaystyle (x,y)}$ in einem bestimmten Bereich zu finden und daraus mithilfe der rekursiven Gleichungen alle weiteren Lösungen zu berechnen. Für diese endlich viele Lösungen ${\displaystyle (x,y)}$ gilt

${\displaystyle |x|\leq {\frac {1}{2}}\cdot {\sqrt {|n|}}\cdot \left({\sqrt {u}}+{\frac {1}{\sqrt {u}}}\right)}$

${\displaystyle |y|\leq {\frac {1}{2\cdot {\sqrt {d}}}}\cdot {\sqrt {|n|}}\cdot \left({\sqrt {u}}+{\frac {1}{\sqrt {u}}}\right)}$

mit ${\displaystyle u:=p+q\cdot {\sqrt {d}}}$.^[12]

Gesucht sind die Lösungen der Gleichung

${\displaystyle x^{2}-7\cdot y^{2}=-3}$

Dafür wird die kleinste Lösung der Gleichung ${\displaystyle x^{2}-7\cdot y^{2}=1}$ bestimmt. Diese lautet ${\displaystyle (p=8,q=3)}$. Also ist ${\displaystyle d=7}$, ${\displaystyle n=-3}$, ${\displaystyle u=8+3\cdot {\sqrt {7}}}$. Es müssen zunächst die Lösungen mit ${\displaystyle |x|\leq {\frac {1}{2}}\cdot {\sqrt {|-3|}}\cdot \left({\sqrt {8+3\cdot {\sqrt {7}}}}+{\tfrac {1}{\sqrt {8+3\cdot {\sqrt {7}}}}}\right)<4}$ bestimmt werden. Das sind ${\displaystyle (x_{0}=-2,y_{0}=-1)}$, ${\displaystyle (x_{0}=-2,y_{0}=1)}$, ${\displaystyle (x_{0}=2,y_{0}=-1)}$ und ${\displaystyle (x_{0}=2,y_{0}=1)}$. Daraus ergeben sich mithilfe der Rekursion alle Lösungen. Aus ${\displaystyle (x_{0}=-2,y_{0}=1)}$ und ${\displaystyle (x_{0}=2,y_{0}=1)}$ erhält man

${\displaystyle (x_{0}=-2,y_{0}=1)}$, ${\displaystyle (x_{1}=5,y_{1}=2)}$, ${\displaystyle (x_{2}=82,y_{2}=31)}$, ${\displaystyle (x_{3}=1307,y_{3}=494)}$, ${\displaystyle (x_{4}=20830,y_{4}=7873)}$, ...

${\displaystyle (x_{0}=2,y_{0}=1)}$, ${\displaystyle (x_{1}=37,y_{1}=14)}$, ${\displaystyle (x_{2}=590,y_{2}=223)}$, ${\displaystyle (x_{3}=9403,y_{3}=3554)}$, ${\displaystyle (x_{4}=149858,y_{4}=56641)}$, ...

Aus ${\displaystyle (x_{0}=2,y_{0}=-1)}$ und ${\displaystyle (x_{0}=-2,y_{0}=-1)}$ ergeben sich die gleichen Lösungen mit umgekehrtem Vorzeichen.

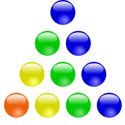
Eine bestimmte Anzahl 1-Euro-Münzen kann sowohl in Form eines Quadrats als auch in Form eines Dreiecks angeordnet werden. Die Bilder rechts veranschaulichen das. Für welche Anzahl von Münzen ist das möglich?

Die gesuchte Anzahl muss sowohl eine Dreieckszahl als auch eine Quadratzahl sein. Daraus erhält man die äquivalenten Gleichungen

${\displaystyle {\begin{aligned}{\frac {n\cdot (n+1)}{2}}&=m^{2}\\{\frac {1}{8}}\cdot ((2\cdot n+1)^{2}-1)&=m^{2}\\(2\cdot n+1)^{2}-2\cdot (2\cdot m)^{2}&=1\\\end{aligned}}}$

Die Substitutionen ${\displaystyle x:=2\cdot n+1}$ und ${\displaystyle y:=2\cdot m}$ ergeben die Pellsche Gleichung

${\displaystyle x^{2}-2\cdot y^{2}=1}$

Die kleinste Lösung ist ${\displaystyle (x_{0}=3,\ y_{0}=2)}$. Aus den rekursiven Gleichungen

${\displaystyle x_{i+1}=x_{0}\cdot x_{i}+2\cdot y_{0}\cdot y_{i}}$

${\displaystyle y_{i+1}=y_{0}\cdot x_{i}+x_{0}\cdot y_{i}}$

erhält man die weiteren Lösungen. Die ersten vier Lösungen mit der entsprechenden Anzahl von Münzen zeigt die folgende Tabelle.^[13]

An einer Straße befinden sich ${\displaystyle n}$ Häuser mit den ungeraden Hausnummern ${\displaystyle 1,3,5,\ldots ,2\cdot n-1}$. Die Häuser sind von links nach rechts durchnummeriert. Eines dieser Häuser ist weiß. Die Summe der Hausnummern links vom weißen Haus ist gleich der Summe der Hausnummern rechts vom weißen Haus. Für welche Anzahl ${\displaystyle n}$ von Häusern ist das möglich? Welche Hausnummer hat dann das weiße Haus?

Hat das weiße Haus die Hausnummer ${\displaystyle 2\cdot m-1}$, dann ist die Summe der Häuser links davon gleich der Summe der Häuser rechts davon:

${\displaystyle {\begin{aligned}1+3+5+\cdots +(2\cdot m-3)&=(2\cdot m+1)+(2\cdot m+3)+\cdots +(2\cdot n-1)\\1+3+5+\cdots +(2\cdot m-3)&=(1+3+5+\cdots +(2\cdot n-1))-(1+3+5+\cdots +(2\cdot m-1))\\\end{aligned}}}$

Jede Quadratzahl ${\displaystyle n^{2}}$ ist die Summe der ersten ${\displaystyle n}$ ungeraden natürlichen Zahlen. Also ist diese Gleichung äquivalent zu

${\displaystyle {\begin{aligned}(m-1)^{2}&=n^{2}-m^{2}\\2\cdot m^{2}-2\cdot m+1&=n^{2}\\4\cdot m^{2}-4\cdot m+2&=2\cdot n^{2}\\(2\cdot m-1)^{2}-2\cdot n^{2}=-1\\\end{aligned}}}$

Die Substitutionen ${\displaystyle x:=2\cdot m-1}$ und ${\displaystyle y:=n}$ ergeben die negative Pellsche Gleichung

${\displaystyle x^{2}-2\cdot y^{2}=-1}$

Die kleinste Lösung ist ${\displaystyle (x_{1}=1,\ y_{1}=1)}$. Aus den rekursiven Gleichungen

${\displaystyle x_{i+1}=x_{0}\cdot x_{i}+2\cdot y_{0}\cdot y_{i}}$

${\displaystyle y_{i+1}=y_{0}\cdot x_{i}+x_{0}\cdot y_{i}}$

erhält man die weiteren Lösungen. Die ersten vier Lösungen mit der Anzahl von Häusern, der größten Hausnummer und der Hausnummer des weiße Hauses zeigt die folgende Tabelle.

Bei der Lösung des Rinderproblems des Archimedes stößt man (wenn man geschickt rechnet) auf die Pellsche Gleichung ${\displaystyle x^{2}-n\cdot y^{2}=1}$ zum Parameter ${\displaystyle n=4729494}$, die als Minimallösung

${\displaystyle x=109931986732829734979866232821433543901088049\approx 1{,}099\cdot 10^{44}}$

${\displaystyle y=\,\qquad 50549485234315033074477819735540408986340\approx 5{,}055\cdot 10^{40}}$

hat. Für das Rinderproblem braucht man allerdings nicht die Minimallösung, sondern die kleinste Lösung, bei der ${\displaystyle y}$ ein Vielfaches von ${\displaystyle 2\cdot 4657}$ ist.

Alternativ dazu kann man für die Pellsche Gleichung mit Parameter ${\displaystyle n=410286423278424=(2\cdot 4657)^{2}\cdot 4729494}$ die Minimallösung (jetzt ohne Nebenbedingung) suchen, die von folgender Größenordnung ist:

${\displaystyle x\approx 3{,}7653\cdot 10^{103272}}$

${\displaystyle y\approx 1{,}8589\cdot 10^{103265}}$

Nicht zufällig ist ${\displaystyle 2\cdot 3{,}7653\cdot 10^{103272}\approx (2\cdot 1{,}0993199\cdot 10^{44})^{2329}}$, wodurch numerisch der Zusammenhang zwischen den Minimallösungen der beiden Pellschen Gleichungen hergestellt ist.

Für das Rinderproblem selbst ist als Zwischenergebnis die Zahl ${\displaystyle 4657\cdot 957\cdot y^{2}\approx 1{,}5401\cdot 10^{206537}}$ von Belang. Das Endergebnis ist das ${\displaystyle 50389082}$-Fache davon, also ca. ${\displaystyle 7{,}760\cdot 10^{206544}}$.^[1]

Gesucht sind die rechtwinkligen Dreiecke mit ganzzahligen Seitenlängen, wo die Kathetenlängen eine bestimmte Differenz haben. Diese Seitenlängen sind sogenannte pythagoreische Tripel mit besonderen Eigenschaften.

Ist ${\displaystyle k}$ die Differenz der Kathetenlängen, dann sind die ganzzahligen Seitenlängen der rechtwinkligen Dreiecke die pythagoreischen Tripel der Form ${\displaystyle (a,a+k,c)}$. Nach dem Satz des Pythagoras gilt dann

${\displaystyle {\begin{aligned}a^{2}+(a+k)^{2}&=c^{2}\\2\cdot a^{2}+2\cdot a\cdot k+k^{2}&=c^{2}\\4\cdot a^{2}+4\cdot a\cdot k+2\cdot k^{2}&=2\cdot c^{2}\\(2\cdot a+k)^{2}-2\cdot c^{2}&=-k^{2}\\\end{aligned}}}$

Die Substitutionen ${\displaystyle x:=2\cdot a+k}$ und ${\displaystyle y:=c}$ ergeben die verallgemeinerte Pellsche Gleichung

${\displaystyle x^{2}-2\cdot y^{2}=-k^{2}}$

Die kleinste Lösung der Gleichung ${\displaystyle x^{2}-2\cdot y^{2}=1}$ ist ${\displaystyle (p=3,q=2)}$.

Für den Fall ${\displaystyle k=1}$ ist ${\displaystyle (x_{0}=1,y_{0}=1)}$ die einzige positive Basislösung der verallgemeinerten Pellschen Gleichung mit ${\displaystyle d=2}$, ${\displaystyle n=-1}$, ${\displaystyle u=3+2\cdot {\sqrt {2}}}$. Die weiteren Lösungen mit den entsprechenden Seitenlängen der rechtwinkligen Dreiecke sind

Für ${\displaystyle (x_{0}=1,y_{0}=1)}$ ist ${\displaystyle a=0}$. Daher gehört diese Lösung zu keinem Dreieck. Die Seitenlängen der gesuchten rechtwinkligen Dreiecke sind (3, 4, 5), (20, 21, 29), (119, 120, 169), ... Das sind die rechtwinkligen Dreiecke, wo die Kathetenlängen die Differenz ${\displaystyle k=1}$ haben. Für ${\displaystyle k=2,3,4,5,6}$ sind die Lösungen der verallgemeinerten Pellsche Gleichung die entsprechenden Vielfachen. Für die Differenz ${\displaystyle k=6}$ zum Beispiel ergeben sich die rechtwinkligen Dreiecke mit den Seitenlängen (18, 24, 30), (120, 126, 174), (714, 720, 1014), ...

Für ${\displaystyle k=7}$ hat die verallgemeinerte Pellsche Gleichung mehrere Basislösungen, darunter ${\displaystyle (x_{0}=-1,y_{0}=5)}$, ${\displaystyle (x_{0}=1,y_{0}=5)}$ und ${\displaystyle (x_{0}=7,y_{0}=7)}$. Daraus ergeben sich alle weiteren positiven Lösungen und, wenn alle positiv, die entsprechenden Seitenlängen der rechtwinkligen Dreiecke:

Gesucht sind gleichseitige Dreiecke, die in zwei Teildreiecke mit ganzzahligen Seitenlängen zerlegt werden können.

Ist ${\displaystyle a}$ die Seitenlänge und ${\displaystyle h}$ die Höhe des gleichseitigen Dreiecks, ist ${\displaystyle t}$ die Länge der Strecke, die das gleichseitige Dreieck teilt, und sind ${\displaystyle s}$ und ${\displaystyle a-s}$ die Längen der geteilten Seite, dann bildet die Höhe zusammen mit der Teilungsstrecke und einer Strecke der Länge ${\displaystyle k:={\frac {a}{2}}-s}$ ein rechtwinkliges Dreieck, wobei ${\displaystyle t}$ die Hypotenusenlänge ist. Die Abbildung rechts zeigt das.

Nach dem Satz des Pythagoras und wegen ${\displaystyle h^{2}={\frac {3}{4}}\cdot a^{2}}$ gilt dann

${\displaystyle {\begin{aligned}h^{2}+k^{2}&=t^{2}\\{\frac {3}{4}}\cdot a^{2}+k^{2}&=t^{2}\\t^{2}-3\cdot \left({\frac {a}{2}}\right)^{2}&=k^{2}\\\end{aligned}}}$

Die Substitutionen ${\displaystyle x:=t}$ und ${\displaystyle y:={\frac {a}{2}}}$ ergeben die verallgemeinerte Pellsche Gleichung

${\displaystyle x^{2}-3\cdot y^{2}=k^{2}}$

Die kleinste Lösung der Gleichung ${\displaystyle x^{2}-3\cdot y^{2}=1}$ ist ${\displaystyle (p=2,q=1)}$.

Für den Fall ${\displaystyle k=1}$ ist ${\displaystyle (x_{0}=2,y_{0}=1)}$ die einzige positive Basislösung der verallgemeinerten Pellschen Gleichung mit ${\displaystyle d=3}$, ${\displaystyle n=1}$, ${\displaystyle u=2+{\sqrt {3}}}$. Die weiteren Lösungen mit die entsprechenden Seitenlänge ${\displaystyle a}$ des gleichseitigen Dreiecks und die Seitenlängen ${\displaystyle s,t,a}$ und ${\displaystyle a-s,a,t}$ der zwei Teildreiecke sind

Für ${\displaystyle k=2,3,4,5,6,7,8,9,10}$ sind die Lösungen der verallgemeinerten Pellsche Gleichung die entsprechenden Vielfachen.

Für den Fall ${\displaystyle k=11}$ hat die verallgemeinerte Pellsche Gleichung mehrere Basislösungen, darunter ${\displaystyle (x_{0}=11,y_{0}=0)}$, ${\displaystyle (x_{0}=13,y_{0}=4)}$ und ${\displaystyle (x_{0}=14,y_{0}=5)}$. Daraus ergeben sich alle weiteren positiven Lösungen und, wenn alle positiv, die entsprechenden Seitenlängen des gleichseitigen Dreiecks und der zwei Teildreiecke:

• H. W. Lenstra Jr.: Solving the Pell Equation, Notices of the American Mathematical Society, Band 49, Heft 2, 2002, S. 182–192, online (PDF; 237 kB).
• M. J. Jacobson Jr., H. C. Williams: Solving the Pell Equation, CMS Books in Mathematics, Springer 2009, ISBN 978-0-387-84922-5
• Leonard Dickson: History of the theory of numbers, Washington D.C.: Carnegie Institution, 1920, Kapitel 12 (zur Geschichte der Pellschen Gleichung)

• Pell Equation in Wolfram’s Math World (englisch)
• Universität Bayreuth: Diophantische Gleichungen (Seite 71)
• Schweizer Mathematik-Olympiade: Zahlentheorie 3 (Seite 5)
• Technische Universität Graz: Zahlentheorie - Vorbereitungskurs zur Österreichischen Mathematischen Olympiade (Seite 39)

1. ↑ ^{a b} Siehe Artikel von H. W. Lenstra Jr.
2. ↑ So auch Dickson, History of the theory of numbers, Band 2, S. 341 (Kapitel 12 zur Geschichte der Pellschen Gleichung)
3. ↑ Noel Malcolm, Jacqueline Steadall: John Pell in his correspondence with Sir Charles Cavendish, Oxford UP, 2005, S. 320
4. ↑ André Weil, Number theory - An approach through history from Hammurapi to Legendre, Birkhäuser 1984, S. 174
5. ↑ Dickson, History of the theory of numbers, Band 2, Carnegie Institution 1920, S. 353. Er benutzte seine Methode des unendlichen Abstiegs
6. ↑ Max Lahn, Jonathan Spiegel: Continued Fractions and Pell’s Equation. In: Mixed Math - Explorations in math and number theory. David Lowry-Duda, Mai 2016, abgerufen am 31. Mai 2020 (englisch). 
7. ↑ Erick Knight, Stanley Yao Xiao, University of Toronto: The Negative Pell Equation
8. ↑ Keith Conrad, University of Connecticut: Pell’s Equation
9. ↑ Wolfram MathWorld: Pell Equation
10. ↑ A002350, auf oeis.org
11. ↑ A002349, auf oeis.org
12. ↑ Keith Conrad, University of Connecticut: Pell’s Equation
13. ↑ Wolfram MathWorld: Square Triangular Number