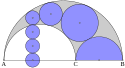
Pappos-Kette

Die Pappos-Kette im Arbelos

Die Pappos-Kette (auch Pappus-Kette) ist in der Geometrie eine unendliche Folge einander berührender Kreise in einem Arbelos. Sie ist benannt nach dem griechischen Geometer Pappos von Alexandria, der sie im 3. Jahrhundert erstmals untersuchte.

Konstruktion

Pappos-Kette im gespiegelten Arbelos

Ein Arbelos wird gebildet durch die drei Halbkreise über ${\displaystyle AB}$, ${\displaystyle AC}$ und ${\displaystyle CB}$ (sichelförmige Figur in der oberen Abbildung). Der Inkreis des Arbelos mit dem Mittelpunkt ${\displaystyle P_{1}}$ ist der erste Kreis der Pappos-Kette, die weiteren (mit den Mittelpunkten ${\displaystyle P_{2}}$, ${\displaystyle P_{3}}$ u. s. f.) ergeben sich durch Aneinanderreihung von Kreisen, die den jeweils vorangehenden Kreis der Kette, den großen Halbkreis über ${\displaystyle AB}$ und einen der beiden kleineren Halbkreise berühren. In der Abbildung, auf die sich auch der weitere Text bezieht, ist das der linke Halbkreis über ${\displaystyle AC}$, die Kette hätte ebenso gut nach rechts (den Halbkreis über ${\displaystyle CB}$ berührend) fortgesetzt werden können.

Man kann die Pappos-Kette auch in einem an ${\displaystyle AB}$ gespiegelten Arbelos betrachten, dann wird der zum Kreis ergänzte Arbelos-Halbkreis, der nicht alle Kreise der Kette berührt (hier der über ${\displaystyle CB}$), zu einem Glied der Kette.

Eigenschaften

Abstand des Kreises 3 von der Arbelos-Grundlinie

Man nummeriere die Kreise der Pappos-Kette wie folgt: Der zum Kreis ergänzte Arbelos-Halbkreis über ${\displaystyle CB}$ erhält die Nummer 0, der Arbelos-Inkreis die Nummer 1 u. s. f. (entsprechend der Indizierung der Kreismittelpunkte ${\displaystyle P_{n}}$ in der oberen Abbildung), die Radien dieser Kreise bezeichne man mit ${\displaystyle r_{n}}$. Die Radien der beiden kleinen Arbelos-Halbkreise seien ${\displaystyle a={\overline {CB}}/2=r_{0}}$ und ${\displaystyle b={\overline {AC}}/2}$.

• Der Kreis mit der Nummer ${\displaystyle n}$ hat den Radius
  ${\displaystyle r_{n}={\frac {ab(a+b)}{n^{2}a^{2}+b(a+b)}}}$.
• Der Mittelpunkt ${\displaystyle P_{n}}$ des Kreises mit der Nummer ${\displaystyle n}$ hat den Abstand ${\displaystyle 2nr_{n}}$ von der Arbelos-Grundlinie ${\displaystyle AB}$. Die Abbildung rechts illustriert dies für den Kreis mit der Nummer 3.
• Die Mittelpunkte der Kreise der Pappos-Kette liegen auf einer Ellipse (gestrichelt in der oberen Abbildung). Die Brennpunkte dieser Ellipse sind die Mittelpunkte der Strecken ${\displaystyle AB}$ und ${\displaystyle AC}$.
• Die Punkte, in denen die Kreise der Pappos-Kette einander berühren, liegen auf einem Kreis.

Siehe auch

• Steiner-Kette
• Buch der Lemmata

Weblinks

Commons: Pappus chain – Sammlung von Bildern

• Jürgen Köller: Pappus-Kette. Mathematische Basteleien.
• Bob Allanson: Pappus’s Arbelos (animiertes Java-Applet, englisch)
• Walter Fendt: Die Pappos-Kette. (HTML5-App). HTML5-Apps zur Mathematik.
• Floor van Lamoen, Eric W. Weisstein: Pappus Chain. In: MathWorld (englisch).