Orthogonale Axonometrie

Die orthogonale (senkrechte) Axonometrie bietet ein relativ einfaches Verfahren, um aus zwei zugeordneten Rissen (Grund- und Aufriss) eine orthogonale Parallelprojektion eines Objektes herzustellen. Dabei bedient man sich eines Einschneideverfahrens, für das zwar die Bilder der Koordinatenachsen noch (fast) frei gewählt werden können, aber die Orientierungen von Grund- und Aufriss mit dieser Wahl schon fest liegen (s. unten). Die Vorteile einer orthogonalen Axonometrie sind a) gute Bildwirkung, b) frei wählbare Projektionsrichtung, c) Umriss einer Kugel ist ein Kreis d) schnelles Einschneideverfahren: Man muss nicht einzelne Koordinaten verkürzen und antragen. Es genügt, Parallelen zu den Einschneiderichtungen zu zeichnen und zugeordnete Strahlen zu schneiden.

Beschreibung des Verfahrens

Man geht von einem Grundriss in der xy-Ebene und einem Aufriss in der yz-Ebene aus.

1. Man wähle in der Bildtafel (Zeichenebene) die Bilder der 3 Koordinatenachsen (nicht alle auf einer Gerade).
2. Auf einer der Achsen, z. B. x-Achse, wählt man einen Punkt als Spurpunkt der Bildtafel, z. B. ${\displaystyle S_{x}}$ und konstruiert die Spurpunkte ${\displaystyle S_{y},S_{z}}$ unter Beachtung, dass die Bilder der Koordinatenachsen die Höhen im Spurpunktdreieck sind. (Das Bild des Koordinatenursprungs ist der Höhenschnittpunkt.)
3. Der Schnitt des Thaleskreises über ${\displaystyle S_{x},S_{y}}$ mit dem Bild der z-Achse liefert den in die Bildtafel hineingedrehten Nullpunkt ${\displaystyle {\tilde {O}}'}$ des Grundrisses. Durch Herausziehen des Umgeklappten Grundrisses in Richtung des Bildes der z-Achse (1. Einschneiderichtung) ergibt sich die Lage des Grundrisses für das anschließende Einschneideverfahren.
4. Analog verfährt man, um die Lage des Aufrisses für das Einschneideverfahren zu bestimmen.
5. Durchführung des Einschneideverfahrens.

Begründung des Verfahrens

Eine orthogonale Parallelprojektion ist durch Angabe der Projektionsrichtung ${\displaystyle \mathbf {p} }$ eindeutig bestimmt. Die Bildtafel ist senkrecht zur Projektionsrichtung und kann entlang der Projektionsrichtung beliebig verschoben werden. Um ein anschauliches Bild von dem räumlichen Objekt zu erhalten, wählt man eine Projektionsrichtung nicht parallel zu einer der Koordinatenachsen. Also schneiden die 3 Koordinatenachsen die Bildtafel in Spurpunkten ${\displaystyle S_{x},S_{y},S_{z}}$, dem Spurpunktdreieck. Mit der Wahl eines Spurpunktes liegen die restlichen beiden fest. Die Bilder der Koordinatenachsen sind die Höhen des Spurpunktdreiecks und das Bild des Koordinatenursprungs der Schnittpunkt dieser Höhen. Beim Umklappen der Grundrissebene (xy-Ebene) um die Spurgerade ${\displaystyle S_{x}S_{y}}$ bewegt sich das Bild des Nullpunktes ${\displaystyle {\overline {O}}}$ auf der ${\displaystyle {\overline {z}}}$-Achse in den Punkt ${\displaystyle {\tilde {O}}'}$. Die Spurpunkte ${\displaystyle S_{x}S_{y}}$ bleiben bei dem Drehvorgang unverändert. Also ist die Gerade durch ${\displaystyle S_{x},{\tilde {O}}'}$ die in die Bildtafel geklappte x-Achse. Analog erhält man die umgeklappte y-Achse und damit die unverzerrte Grundrissebene (xy-Ebene). Um das zu zeichnende Bild nicht zu stören, zieht man den Grundriss in Richtung der ${\displaystyle {\overline {z}}}$-Achse nach unten. Analog verfährt man mit dem Aufriss (yz-Ebene). Die für das Einschneideverfahren wichtigen Einschneiderichtungen sind die Richtungen der ${\displaystyle {\overline {z}}}$-Achse und ${\displaystyle {\overline {x}}}$-Achse.

Kugel und Kreis

Kugeln sind in orthogonaler Axonometrie besonders leicht abzubilden: Der Umriss einer Kugel ist ein Kreis mit dem Radius der Kugel. Um eine Kugel abzubilden, muss also nur das Bild des Mittelpunktes der Kugel bestimmt und dann der Umrisskreis gezeichnet werden. In einer schiefen Parallelprojektion ist der Umriss einer Kugel immer eine Ellipse, deren Achsen erst mühsam bestimmt werden müssen.

Die Parallelprojektion eines Kreises, der zur Bildtafel parallel ist, ist ein unverzerrter Kreis. In jedem anderen Fall wird ein Kreis auf eine Ellipse abgebildet, deren Mittelpunkt das Bild des Kreismittelpunktes ist. Die Richtungen der Hauptachsen und die Größe der Halbachsen müssen i. a. mit der Rytz-Konstruktion bestimmt werden.

Bei einer orthogonalen Parallelprojektion wird derjenige Durchmesser eines Kreises, der parallel zur Bildtafel ist, unverzerrt auf die große Hauptachse der Bildellipse abgebildet. D. h. Mittelpunkt, die Hauptachsenrichtungen und die große Halbachse (= Kreisradius) sind im Bild bekannt. Die Größe der kleinen Halbachse ermittelt man gemäß der Abbildung „Ellipse: Punkt-Konstruktion mit Hilfe der Scheitelkreise“, indem man die Kenntnis der großen Hauptachse und eines Ellipsenpunktes voraussetzt. Im Beispiel sind Boden- und Deckelkreise eines Zylinders parallel zur xy-Ebene. Geraden der xy-Ebene, die parallel zur Bildtafel sind, sind alle parallel zur Spurgerade ${\displaystyle S_{x}S_{y}}$. Also wird der Durchmesser des Bodenkreises, der parallel zu dieser Spurgerade ist, unverzerrt abgebildet. Als Ellipsenpunkt zur Konstruktion der kleinen Halbachse wird hier der Kreispunkt auf der x-Achse verwendet. Das Bild des Deckelkreises des Zylinders ist das Bild des Bodenkreises in den Deckel verschoben.

Alternative Vorgaben

Statt der oben angegebenen Vorgabe der Achsenbilder kann man auch

• das Spurpunktdreieck vorgeben. Die Achsenbilder sind dann die Höhen dieses Dreiecks und das Bild des Koordinatenursprungs ist der Höhenschnittpunkt.
• die Projektionsrichtung ${\displaystyle \mathbf {p} }$ in Grund- und Aufriss vorgeben (s. Bild). Zur Konstruktion des Spurpunktdreiecks wählt man einen beliebigen Punkt der x-Achse als ${\displaystyle S_{x}}$. Da die Spur ${\displaystyle S_{x}S_{y}}$ senkrecht zu ${\displaystyle \mathbf {p} '}$ verlaufen muss, ergibt sich ${\displaystyle S_{y}}$ als Schnittpunkt des Lotes von ${\displaystyle S_{x}}$ auf ${\displaystyle \mathbf {p} '}$ mit der y-Achse im Grundriss. Mit dem analogen Argument im Aufriss findet man ${\displaystyle S_{z}}$ (s. Bild). Die Längen der Seiten ${\displaystyle S_{x}S_{y}}$ und ${\displaystyle S_{y}S_{z}}$ erkennt man im Grund- bzw. Aufriss. Die Länge von ${\displaystyle S_{x}S_{z}}$ ergibt sich durch Paralleldrehen zur Aufrissebene (s. wahre Länge). Damit sind alle Seitenlängen des Spurpunktdreiecks bekannt und das Dreieck kann gezeichnet werden. (Die Zahlen in der Zeichnung geben die Reihenfolge der Konstruktionsschritte an.)

Umkehrung des Verfahrens

Geht man von einem Bild in orthogonaler Parallelprojektion aus, bei dem die Bilder der Achsen erkennbar sind, so lässt sich die Umkehrung des obigen Einschneideverfahrens dazu benutzen, um Grund- und Aufriss zu rekonstruieren. Auch die Projektions-Richtung ist in der Rekonstruktion zu erkennen.

Beispiel: Rekonstruktion eines Aufrisses

Gegeben: orthogonale Axonometrie eines Kreuzgewölbes.

Gesucht: ein Aufriss, um die wahren Maße festzustellen.

Lösungsschritte:

1. Wahl eines Spurpunktes: hier der Mittelpunkt des rechten Randkreises.
2. Vervollständigung des Spurdreiecks (rot, s. o.)
3. Herausziehen des rechten Aufrisses: a) Parallele zur rechten Dreiecksseite, zugehörige Spurpunkte, Thaleskreis. b) Schnitt des Thaleskreises mit der zugehörigen Einschneidegerade durch den Ursprung. c) Zeichnen der Aufrissachsen.
4. Rekonstruktion wesentlicher Punkte (s. Zeichnung).

Mögliche Verkürzungen

Bei einer orthogonalen Axonometrie können, im Gegensatz zu einer allgemeinen Axonometrie, nicht beliebige Verkürzungen ${\displaystyle v_{x},v_{y},v_{z}}$ auftreten. Man sieht leicht ein (siehe oben), dass alle Verkürzungen kleiner oder gleich ${\displaystyle 1}$ sind. Aber nicht beliebige drei Zahlen kleiner oder gleich ${\displaystyle 1}$ können als Verkürzungen auftreten. Um festzustellen, welche Tripel möglich sind, werden die Verkürzungen für eine beliebige orthogonale Axonometrie bestimmt:

Die Bildtafel möge den Nullpunkt des Koordinatensystems enthalten und die negative Projektionsrichtung ${\displaystyle {\vec {n}}}$ (Einheitsnormale der Bildebene) werde durch den Ortsvektor eines Punktes auf der Einheitskugel beschrieben. Die Projektion lässt sich alo so beschreiben:

${\displaystyle {\vec {x}}\ \rightarrow {\vec {x}}-({\vec {x}}\cdot {\vec {n}}){\vec {n}}\quad }$ mit

${\displaystyle {\vec {n}}=(\cos u\cos v,\sin u\cos v,\sin v)^{T}\ ,\quad 0\leq u,v\leq \pi /2\ .}$

Die Winkel ${\displaystyle u,v}$ kann man sich als geographische Länge bzw. Breite vorstellen. Die Normalenvektoren liegen im 1. Oktanten der Einheitskugel.

Die Bilder der Basisvektoren ${\displaystyle {\vec {e}}_{1}=(1,0,0)^{T},{\vec {e}}_{2}=(0,1,0)^{T},{\vec {e}}_{3}=(0,0,1)^{T}}$ sind:

${\displaystyle {\vec {f}}_{i}={\vec {e}}_{i}-({\vec {e}}_{i}\cdot {\vec {n}})\;{\vec {n}}\ ,\ i=1,2,3\ .}$

Deren Längen ${\displaystyle {\sqrt {({\vec {e}}_{i}-({\vec {e}}_{i}\cdot {\vec {n}})\;{\vec {n}})^{2}}}={\sqrt {1-(e_{i}\cdot {\vec {n}})^{2}}}}$ sind die axonometrischen Verkürzungen:

• ${\displaystyle v_{x}={\sqrt {1-(\cos u\cos v)^{2}}},\quad v_{y}={\sqrt {1-(\sin u\cos v)^{2}}},\quad v_{z}=\cos v\ }$

Hieraus ergibt sich ^[1]

• ${\displaystyle v_{x}^{2}+v_{y}^{2}+v_{z}^{2}=2\ ,\quad v_{x},v_{y},v_{z}\leq 1.}$

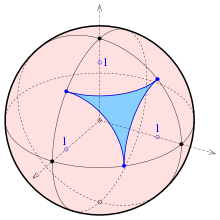
Es sind also nur solche Verkürzungen möglich, die Koordinaten von Punkten der Kugel ${\displaystyle \ x^{2}+y^{2}+z^{2}=2\ }$ sind und dort innerhalb des durch ${\displaystyle \ x=1,\;y=1,\;z=1\ }$ beschriebenen Kreisdreiecks liegen (siehe Bild).

Um die Winkel ${\displaystyle \alpha ,\beta }$ zwischen den Bildern des 1. und 3. bzw. 2. und 3. Basisvektors zu bestimmen, benötigt man

${\displaystyle {\vec {f}}_{i}\cdot {\vec {f}}_{k}=-({\vec {e}}_{i}\cdot {\vec {n}})({\vec {e}}_{k}\cdot {\vec {n}})\ ,\quad i\neq k\ .}$

Es ist

${\displaystyle \cos \alpha ={\frac {-({\vec {e}}_{1}\cdot {\vec {n}})({\vec {e}}_{3}\cdot {\vec {n}})}{v_{x}v_{z}}}={\frac {-\cos u\sin v}{\sqrt {1-(\cos u\cos v)^{2}}}}\ ,\ }$

${\displaystyle \cos \beta ={\frac {-({\vec {e}}_{2}\cdot {\vec {n}})({\vec {e}}_{3}\cdot {\vec {n}})}{v_{y}v_{z}}}={\frac {-\sin u\sin v}{\sqrt {1-(\sin u\cos v)^{2}}}}\ .}$

Ingenieuraxonometrie

Für die Ingenieuraxonometrie ist ${\displaystyle \ v_{y}=v_{z}=2v_{x}\ }$.
Einsetzen in die Kugelgleichung liefert ${\displaystyle \ {\tfrac {v_{z}^{2}}{4}}+v_{z}^{2}+v_{z}^{2}=2}$ und daraus

• ${\displaystyle v_{z}={\frac {2{\sqrt {2}}}{3}}=v_{y},\quad v_{x}={\frac {\sqrt {2}}{3}}\ .}$

Aus ${\displaystyle \ v_{z}={\tfrac {2{\sqrt {2}}}{3}}=\cos v\ }$ folgt ${\displaystyle \ v=19{,}47^{\circ }\ .}$

Aus ${\displaystyle \ {\tfrac {8}{9}}=v_{y}^{2}=1-(\sin u\cos v)^{2}\ }$ und ${\displaystyle \ \cos ^{2}v={\tfrac {8}{9}}\ }$ ergibt sich ${\displaystyle \ \sin ^{2}u={\tfrac {1}{8}}\;}$ und ${\displaystyle \ u=20{,}7^{\circ }\ }$. Also ist

${\displaystyle {\vec {n}}=({\tfrac {\sqrt {7}}{3}},{\tfrac {1}{3}},{\tfrac {1}{3}})^{T}\;,}$

${\displaystyle {\vec {f}}_{1}=-{\frac {1}{9}}(-2,{\sqrt {7}},{\sqrt {7}})^{T}\;,\quad {\vec {f}}_{2}=-{\frac {1}{9}}({\sqrt {7}},-8,1)^{T}\;,\quad {\vec {f}}_{3}=-{\frac {1}{9}}({\sqrt {7}},1,-8)^{T}\ .}$

${\displaystyle \cos \alpha =-{\frac {\sqrt {7}}{4}}\quad \to \quad \alpha =131{,}41^{\circ }\quad ,}$

${\displaystyle \cos \beta =-{\frac {1}{8}}\qquad \to \quad \beta =97{,}18^{\circ }\quad .}$

Um die für die Ingenieuraxonometrie üblichen Verkürzungen ${\displaystyle v_{x}=0{,}5,v_{y}=v_{z}=1}$ zu erreichen, muss man an die orthogonale Projektion noch eine Skalierung mit dem Faktor ${\displaystyle {\tfrac {3}{2{\sqrt {2}}}}=1{,}06}$ anschließen. (Eine Skalierung ändert die Winkel ${\displaystyle u,v}$ nicht.)

Isometrie

Für eine Isometrie gilt ${\displaystyle \;v_{x}=v_{y}=v_{z}\;}$. Einsetzen in die Kugelgleichung liefert

• ${\displaystyle v_{x}=v_{y}=v_{z}={\sqrt {\tfrac {2}{3}}}\ .}$

Setzt man dieses Ergebnis in die Gleichungen für die Verkürzungen ein, erhält man zunächst ${\displaystyle \cos v={\sqrt {\tfrac {2}{3}}}}$ und damit ${\displaystyle \cos u={\tfrac {1}{\sqrt {2}}}}$. Die Projektionswinkel sind

${\displaystyle u=45^{\circ }\;,\ v=35{,}26^{\circ }\ .}$

Damit ist

${\displaystyle {\vec {n}}={\frac {1}{\sqrt {3}}}(1,1,1)\ ,}$

${\displaystyle {\vec {f}}_{1}={\frac {1}{3}}(2,-1,-1)\;,\ {\vec {f}}_{2}={\frac {1}{3}}(-1,2,-1)\;,\ {\vec {f}}_{3}={\frac {1}{3}}(-1,-1,2)\ }$ und

${\displaystyle \alpha =\beta =120^{\circ }\ .}$

Die Standard-Isometrie mit ${\displaystyle \;v_{x}=v_{y}=v_{z}=1\;}$ ergibt sich, wenn man die orthogonale Projektion mit einer Skalierung mit dem Faktor ${\displaystyle \;{\sqrt {\tfrac {3}{2}}}=1{,}22\;}$ kombiniert.

Einzelnachweise

1. ↑ E. L. Stiefel: Lehrbuch der Darstellenden Geometrie. Springer-Verlag, Basel 1947, ISBN 978-3-0348-4098-9, S. 40.

Literatur

• Cornelie Leopold: Geometrische Grundlagen der Architekturdarstellung. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X
• Fucke, Kirch, Nickel: Darstellende Geometrie. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4

Weblinks

• Normale (orthogonale) Axonometrie mit einfachen Beispielen
• Darstellende Geometrie für Architekten (PDF; 1,5 MB). Skript (Uni Darmstadt), S. 42