Molekülstruktur

Geometrie von Wasser mit Bindungslängen und Bindungswinkeln

Als Molekülstruktur oder Molekülgeometrie wird die geometrische, räumliche relative Anordnung der Atome in einem Molekül bezeichnet. Sie bestimmt maßgeblich wichtige Eigenschaften wie das elektrische Dipolmoment.

Eigenschaften

Zur Beschreibung werden meist kartesische Koordinaten (x, y, z) verwendet, um die Positionen der Atome anzugeben, oder auch interne Koordinaten, d. h. Bindungslängen und Bindungswinkel und ggf. Diederwinkel. Diese können durch das Auftreten von Symmetrien usw. in 32 Punktgruppen zusammengefasst werden. Die Beschreibung erfolgt typischerweise in der nach Arthur Schoenflies benannten Schoenflies-Symbolik.

Experimentell kann die Molekülstruktur mittels Kristallstrukturanalyse oder Kernspinresonanzspektroskopie (NMR) ermittelt werden. Für kleine Moleküle aus wenigen Atomen kann die Struktur auch mit den Methoden der Theoretischen Chemie berechnet werden. Eine ungefähre Abschätzung ist mit dem VSEPR-Modell möglich.

Beispiele

Atome am Zentralatom	Freie Elektronenpaare	Sterische Zahl	Form	Idealer Bindungswinkel (Bsp.)	Beispiel	Bild
2	0	2	linear	180°	CO2
3	0	3	trigonal-planar	120°	BF3
2	1	3	gebogen	120° (119°)	SO2
4	0	4	tetraedrisch	109,5°	CH4
3	1	4	trigonal-pyramidal	109,5° (107,8°)	NH3
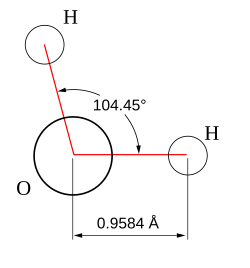
2	2	4	gebogen	109,5° (104,48°)[1][2]	H2O
5	0	5	trigonal-bipyramidal	90°, 120°	PCl5
4	1	5	wippenartig	ax–ax 180° (173,1°), eq–eq 120° (101,6°), ax-eq 90°	SF4
3	2	5	T-förmig	90° (87,5°), 180° (175°)	ClF3
2	3	5	linear	180°	XeF2
6	0	6	octaedrisch	90°, 180°	SF6
5	1	6	quadratisch-pyramidal	90° (84,8°)	BrF5
4	2	6	quadratisch-planar	90°, 180°	XeF4
7	0	7	pentagonal-bipyramidal	90°, 72°, 180°	IF7
6	1	7	pentagonal-pyramidal	72°, 90°, 144°	XeOF5−
5	2	7	pentagonal-planar	72°, 144°	XeF5−
8	0	8	quadratisch-antiprismatisch		XeF8(2−)
9	0	9	tricapped trigonal-prismatisch		ReH9(2−)

Siehe auch

• Strukturchemie
• Strukturaufklärung

Weblinks

Wikibooks: Allgemeine und Anorganische Chemie: Struktur von Molekülen – Lern- und Lehrmaterialien

Einzelnachweise

1. ↑ AR Hoy, PR Bunker: A precise solution of the rotation bending Schrödinger equation for a triatomic molecule with application to the water molecule. In: Journal of Molecular Spectroscopy. 74, Nr. 1, 1979, S. 1–8. bibcode:1979JMoSp..74....1H. doi:10.1016/0022-2852(79)90019-5.
2. ↑ Archived copy. Archiviert vom Original am 3. September 2014. Abgerufen am 27. August 2014.