Modulare Gruppe (M-Gruppe)

Eine modulare Gruppe oder M-Gruppe ist eine im mathematischen Teilgebiet der Gruppentheorie betrachtete Art von Gruppen. Es handelt sich um solche Gruppen, deren Verband der Untergruppen ein modularer Verband ist.

Definitionen

Sind ${\displaystyle U}$ und ${\displaystyle V}$ Untergruppen einer Gruppe ${\displaystyle G}$, so setzt man

${\displaystyle U\land V:=U\cap V}$   =   Schnittmenge der Untergruppen

${\displaystyle U\lor V:=\langle U\cup V\rangle }$   =   von der Vereinigung erzeugte Untergruppe.

Durch ${\displaystyle \land }$ und ${\displaystyle \lor }$ wird die Menge ${\displaystyle {\mathcal {U}}}$ der Untergruppen zu einem Verband mit den trivialen Untergruppen als kleinstem und größtem Element.

Im Allgemeinen ist dieser Verband nicht modular, das heißt, es gilt im Allgemeinen nicht das sogenannte modulare Gesetz:

Aus  ${\displaystyle U\subset W}$   folgt   ${\displaystyle \forall V\in {\mathcal {U}}:\,U\lor (V\land W)=(U\lor V)\land W}$.

Man nennt eine Untergruppe ${\displaystyle V\in {\mathcal {U}}}$ modular, falls

${\displaystyle \forall U\subset W\in {\mathcal {U}}:\,U\lor (V\land W)=(U\lor V)\land W}$.^[1]

Eine Gruppe heißt modulare Gruppe oder M-Gruppe, wenn der Untergruppenverband modular ist, das heißt, wenn jede Untergruppe modular ist.^[2][3]

Hasse-Diagramm des Untergruppenverbandes von D₄, die Untergruppen sind durch ihre Zykel-Graphen dargestellt.

D₄ ist nicht modular

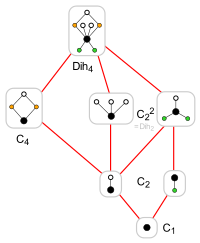
Die Diedergruppe D₄ ist nicht modular, wie man leicht an nebenstehender Darstellung des Untergruppenverbandes abliest, denn offensichtlich enthält er einen zu N₅ isomorphen Unterverband. Die Verletzung des modularen Gesetzes kann konkret angegeben werden: ${\displaystyle U}$ sei die am weitesten links stehende zweielementige Untergruppe, ${\displaystyle W}$ die oberhalb davon liegende vierelementige Untergruppe und ${\displaystyle V}$ die am weitesten rechts stehende zweielementige Untergruppe. Man liest ab: ${\displaystyle V\land W=\{e\}}$, ${\displaystyle U\lor V=D_{4}}$ und daher

${\displaystyle U\lor (V\land W)=U\subsetneq W=(U\lor V)\land W}$.

Also ist ${\displaystyle D_{4}}$ nicht modular, sie ist die kleinste nicht-modulare Gruppe. ${\displaystyle V\subset D_{4}}$ ist ein Beispiel für eine nicht-modulare Untergruppe.

Vergleich mit Dedekindgruppen

Normalteiler sind modulare Untergruppen.

Daher sind dedekindsche Gruppen modular, denn dies sind definitionsgemäß genau die Gruppen, in denen jede Untergruppe Normalteiler ist.

Insbesondere sind alle abelschen Gruppen modular.

Unter den Dedekindgruppen gibt es auch nichtabelsche Gruppen; solche nennt man Hamiltongruppen. Die Quaternionengruppe Q₈ ist daher ein Beispiel einer nichtabelschen modularen Gruppe.

Es gibt modulare Gruppen, die keine Dedekindgruppen sind, siehe Beispiel unten.

Endliche p-Gruppen

Eine endliche p-Gruppe ist genau dann modular, wenn jeder Subquotient der Ordnung ${\displaystyle p^{3}}$ es ist. Für 2-Gruppen bedeutet dies, dass nicht-modulare Gruppen einen zur Diedergruppe D₄ isomorphen Subquotienten haben müssen, für p>2 muss es im nicht-modularen Fall einen nichtabelschen Subquotienten der Ordnung ${\displaystyle p^{3}}$ geben.^[4]

Die Struktur der modularen endlichen p-Gruppen ist 1941 von K. Iwasawa aufgedeckt worden:^[5]

Eine p-Gruppe ${\displaystyle G}$ ist genau dann modular, wenn gilt

(a) ${\displaystyle G\cong Q_{8}\times \mathbb {Z} _{2}^{n},\quad n\geq 0}$ (hamiltonscher, nichtabelscher Fall)

oder

(b) Es gibt einen abelschen Normalteiler ${\displaystyle N\subset G}$ mit zyklischer Faktorgruppe ${\displaystyle G/N}$ sowie ein ${\displaystyle x\in G}$ und eine natürliche Zahl ${\displaystyle s}$ (mit ${\displaystyle s\geq 2}$ falls ${\displaystyle p=2}$), so dass ${\displaystyle G}$ von ${\displaystyle N\cup \{x\}}$ erzeugt wird und ${\displaystyle xax^{-1}=a^{1+p^{s}}\,\forall a\in N}$.^[6][7]

Beispiele

Wir verdeutlichen obigen Struktursatz von Iwasawa durch Gruppen der Ordnung 16.

Eine nicht-hamiltonsche, nichtabelsche Gruppe der Ordnung 16

Wir stellen hier ein Beispiel einer nicht-hamiltonschen und nichtabelschen Gruppe mit 16 Elementen vor. Beachte, dass die Multiplikation mit 5 modulo 8 ein Automorphismus ${\displaystyle \alpha }$ auf der zyklischen Gruppe ${\displaystyle \mathbb {Z} _{8}}$ ist. Es ist ${\displaystyle \alpha \circ \alpha =\mathrm {id} _{\mathbb {Z} _{8}}}$, denn dies ist die Multiplikation mit 25 und das ist die Identität, da 25 gleich 1 modulo 8 ist. Daher ist

${\displaystyle \theta :\mathbb {Z} _{2}\rightarrow \mathrm {Aut} (\mathbb {Z} _{8}),\,\theta (0)=\mathrm {id} _{\mathbb {Z} _{8}},\,\theta (1)=\alpha }$

ein Homomorphismus von ${\displaystyle \mathbb {Z} _{2}}$ in die Automorphismengruppe von ${\displaystyle \mathbb {Z} _{8}}$ und man kann das semidirekte Produkt ${\displaystyle G=\mathbb {Z} _{8}\rtimes _{\theta }\mathbb {Z} _{2}}$ bilden.

Die Verknüpfung in dieser Gruppe ist

${\displaystyle (a,b)\cdot (c,d)=(a+5^{b}c;b+d),\quad a,c\in \{0,\ldots ,7\},\,b,d\in \{0,1\}}$,

wobei in der ersten Komponente modulo 8 gerechnet wird und in der zweiten modulo 2.

In obigem Satz von Iwasawa ist ${\displaystyle N=\mathbb {Z} _{8}\times \{0\}}$ ein abelscher Normalteiler, ${\displaystyle G/N\cong \mathbb {Z} _{2}}$ ist zyklisch, für ${\displaystyle x=(0,1)\in G}$ gilt ${\displaystyle G=\langle N\cup \{x\}\rangle }$ und für alle ${\displaystyle a\in \{0,\ldots ,7\}}$

${\displaystyle x\cdot (a,0)\cdot x=(0,1)\cdot (a,0)\cdot (0,1)=(0+5^{1}a,1)\cdot (0,1)=(5a,1)\cdot (0,1)=(5a+5^{1}\cdot 0,1+1)=(5a,0)=(a,0)^{5}=(a,0)^{1+2^{2}}}$

Diese Gruppe erfüllt damit Teil (b) obigen Satzes von Iwasawa, ist also modular. Sie hat Elemente folgender Ordnungen:

Alle echten Untergruppen sind abelsch, denn als nichtabelsche Untergruppen kämen nach dem Satz von Lagrange nur 8-elementige Untergruppen in Frage, die entweder zu ${\displaystyle Q_{8}}$ oder zur Diedergruppe ${\displaystyle D_{4}}$ isomorph sind (siehe Liste kleiner Gruppen). Erstere hat aber 6 Elemente der Ordnung 4 und letztere hat 5 Elemente der Ordnung 2, sie können also gemäß obiger Liste von Ordnungen nicht in ${\displaystyle G}$ enthalten sein. Insbesondere ist die Gruppe damit nicht hamiltonsch, denn sie müsste sonst eine Kopie von ${\displaystyle Q_{8}}$ enthalten.

Eine nicht-modulare Gruppe der Ordnung 16

Wir ersetzen in obigem Beispiel den Automorphismus ${\displaystyle \alpha }$ durch die Multiplikation mit 3, die ebenfalls ein Automorphismus ${\displaystyle \beta }$ auf ${\displaystyle \mathbb {Z} _{8}}$ ist. Wieder ist ${\displaystyle \beta \circ \beta =\mathrm {id} _{\mathbb {Z} _{8}}}$, denn dies ist die Multiplikation mit 9 modulo 8 und daher die Identität. Also haben wir einen Homomorphismus

${\displaystyle \vartheta :\mathbb {Z} _{2}\rightarrow \mathrm {Aut} (\mathbb {Z} _{8}),\,\vartheta (0)=\mathrm {id} _{\mathbb {Z} _{8}},\,\vartheta (1)=\beta }$

und können damit das semidirekte Produkt ${\displaystyle {\tilde {G}}=\mathbb {Z} _{8}\rtimes _{\vartheta }\mathbb {Z} _{2}}$ bilden. Die Verknüpfung in dieser Gruppe ist

${\displaystyle (a,b)\cdot (c,d)=(a+3^{b}c;b+d),\quad a,c\in \{0,\ldots ,7\},\,b,d\in \{0,1\}}$,

wobei in der ersten Komponente wieder modulo 8 gerechnet wird und in der zweiten modulo 2.

Wieder ist ${\displaystyle N=\mathbb {Z} _{8}\times \{0\}}$ ein abelscher Normalteiler, ${\displaystyle {\tilde {G}}/N\cong \mathbb {Z} _{2}}$ ist zyklisch, für ${\displaystyle x=(0,1)\in {\tilde {G}}}$ gilt ${\displaystyle {\tilde {G}}=\langle N\cup \{x\}\rangle }$ und für alle ${\displaystyle a\in \{0,\ldots ,7\}}$

${\displaystyle x\cdot (a,0)\cdot x=(0,1)\cdot (a,0)\cdot (0,1)=(0+3^{1}a,1)\cdot (0,1)=(3a,1)\cdot (0,1)=(3a+3^{1}\cdot 0,1+1)=(3a,0)=(a,0)^{3}}$.

Das erfüllt nicht die Bedingung (b) aus obigem Satz von Iwasawa für den Fall p=2. Tatsächlich handelt es sich hier um die Quasi-Diedergruppe mit 16 Elementen, und die ist nicht modular. Mit

${\displaystyle U:=\{(0,0),(0,1)\},\ V=\{(0,0),(2,1)\},\,W=\{(0,0),(0,1),(4,0),(4,1)\}}$

bestätigt man leicht

${\displaystyle U\lor (V\land W)=U\subsetneq W=(U\lor V)\land W}$.

Alternativ kann man obige Charakterisierung mittels Subquotienten verwenden, indem man beachtet, dass die Quasi-Diedergruppe eine zur Diedergruppe ${\displaystyle D_{4}}$ isomorphe Untergruppe enthält, die ein nicht-modularer Subquotient der Ordnung 2³ ist, und daher nicht modular sein kann.

Submodulare Untergruppen

Modularität von Untergruppen ist keine transitive Eigenschaft, das heißt, ist ${\displaystyle U}$ eine modulare Untergruppe der Gruppe ${\displaystyle G}$ und ${\displaystyle V}$ eine modulare Untergruppe von ${\displaystyle U}$, so ist ${\displaystyle V}$ im Allgemeinen keine modulare Untergruppe von ${\displaystyle G}$. Daher führt man den folgenden Begriff der submodularen Untergruppe ein, der die transitive Hülle der Relation „ist modulare Untergruppe in“ darstellt:

Eine Untergruppe ${\displaystyle U\subset G}$ heißt submodular, falls es Untergruppen

${\displaystyle U=U_{0}\subset U_{1}\subset \ldots \subset U_{n}=G}$

gibt, so dass ${\displaystyle U_{i}}$ modulare Untergruppe von ${\displaystyle U_{i+1}}$ ist für jedes ${\displaystyle i=0,\ldots ,n-1}$.^[8]

Siehe auch

• Modulares Gesetz von Dedekind

Einzelnachweise

1. ↑ Irene Zimmermann: Submodular subgroups in finite groups, Mathematische Zeitschrift (1989), Band 202,4 Seiten 545–557
2. ↑ Michio Suzuki: Structure of a Group and the Structure of its Lattice of Subgroups, Springer-Verlag 1956, ISBN 978-3-642-52760-9, Kap. I, §4: Finite Groups with a Modular Lattice of Subgroups
3. ↑ L.N. Shevrin, A.J. Ovsyannikov: Semigroups and Their Subsemigroup Lattices, Springer-Verlag (2013), ISBN 94-015-8751-5, Kapitel II, 6.4
4. ↑ Roland Schmidt: Subgroup Lattices of Groups, De Gruyter Mouton (1994), ISBN 978-3-11-011213-9, Lemma 2.3.3
5. ↑ K. Iwasawa: Über die endlichen Gruppen und die Verbände ihrer Untergruppen, J. Univ. Tokyo (1941), Seiten 171–199.
6. ↑ Michio Suzuki: Structure of a Group and the Structure of its Lattice of Subgroups, Springer-Verlag 1956, ISBN 978-3-642-52760-9, Kap. I, §4: Theorem 14
7. ↑ Roland Schmidt: Subgroup Lattices of Groups, De Gruyter Mouton (1994), ISBN 978-3-11-011213-9, Theorem 2.3.1
8. ↑ Irene Zimmermann: Submodular subgroups in finite groups, Mathematische Zeitschrift (1989), Band 202,4 Seiten 545–557