Messbare Funktion

Messbare Funktionen (englisch measurable functions) werden in der Maßtheorie untersucht, einem Teilbereich der Mathematik, der sich mit der Verallgemeinerung von Längen- und Volumenbegriffen beschäftigt. Von messbaren Funktionen wird verlangt, dass das Urbild gewisser Mengen wieder in einem bestimmten Mengensystem liegt. Messbare Funktionen spielen eine wichtige Rolle in der Stochastik und der Maßtheorie, da durch sie Zufallsvariablen und Bildmaße konstruiert werden können.

Definition

Gegeben seien zwei Messräume ${\displaystyle (X_{1},{\mathcal {A}}_{1})}$ und ${\displaystyle (X_{2},{\mathcal {A}}_{2})}$, das heißt je eine Grundmenge und eine σ-Algebra auf dieser Menge, sowie eine Funktion (bzw. Abbildung)

${\displaystyle f\colon X_{1}\to X_{2}}$.

${\displaystyle \,f\,}$ heißt nun eine messbare Funktion (bzw. messbare Abbildung), wenn das ${\displaystyle \,f}$-Urbild jeder messbaren Menge ${\displaystyle A_{2}\in {\mathcal {A}}_{2}}$ eine messbare Menge von ${\displaystyle {\mathcal {A}}_{1}}$ ist.

Formalisiert lautet diese Bedingung:

${\displaystyle f^{-1}(A_{2})\in {\mathcal {A}}_{1}}$, für alle ${\displaystyle A_{2}\in {\mathcal {A}}_{2}}$^{[A 1]}, wobei ${\displaystyle f^{-1}(A_{2}):=\{x\in X_{1}:f(x)\in A_{2}\}.}$

Eine solche Funktion (bzw. Abbildung) wird auch als ${\displaystyle {\mathcal {A}}_{1}}$-${\displaystyle {\mathcal {A}}_{2}}$-messbar bezeichnet. Falls klar ist, welche Messräume beteiligt sind, sagt man oft auch einfach, ${\displaystyle \,f\,}$ sei messbar.

Eine Funktion heißt Borel-messbar (Lebesgue-messbar), wenn sie bezüglich zweier Borelscher σ-Algebren (Lebesguescher σ-Algebren) messbar ist. Teilweise werden auch Mischformen (Lebesgue-Borel-messbar oder Borel-Lebesgue-messbar) verwendet. Zu beachten ist, dass kein Maß definiert sein muss, um eine messbare Funktion zu definieren.

Elementare Beispiele

• Sind zwei Messräume ${\displaystyle (X_{1},{\mathcal {A}}_{1})}$ und ${\displaystyle (X_{2},{\mathcal {A}}_{2})}$ gegeben, und ist ${\displaystyle {\mathcal {A}}_{2}=\{\emptyset ,X_{2}\}}$ die triviale σ-Algebra, so ist jede Funktion ${\displaystyle f\colon X_{1}\to X_{2}}$ ${\displaystyle {\mathcal {A}}_{1}}$-${\displaystyle {\mathcal {A}}_{2}}$-messbar, unabhängig von der Wahl der Funktion und der σ-Algebra ${\displaystyle {\mathcal {A}}_{1}}$. Dies liegt daran, dass immer ${\displaystyle f^{-1}(\emptyset )=\emptyset }$ und ${\displaystyle f^{-1}(X_{2})=X_{1}}$ gilt. Diese Mengen sind aber immer in der σ-Algebra ${\displaystyle {\mathcal {A}}_{1}}$ enthalten. Wählt man hingegen als σ-Algebra die Potenzmenge ${\displaystyle {\mathcal {A}}_{1}={\mathcal {P}}(X_{1})}$, so ist ebenfalls jede Funktion ${\displaystyle f\colon X_{1}\to X_{2}}$ ${\displaystyle {\mathcal {A}}_{1}}$-${\displaystyle {\mathcal {A}}_{2}}$-messbar, unabhängig von der Wahl der Funktion und der σ-Algebra ${\displaystyle {\mathcal {A}}_{2}}$. Dies liegt daran, dass jedes Urbild ${\displaystyle f^{-1}(A)}$ immer in der Potenzmenge liegt, da diese per Definition jede Teilmenge der Obermenge enthält.
• Jede konstante Funktion, also jede Funktion der Form ${\displaystyle f(x_{1})=c}$ für alle ${\displaystyle x_{1}\in X_{1}}$, ist messbar. Ist nämlich ${\displaystyle A\in {\mathcal {A}}_{2}}$, so ist

${\displaystyle f^{-1}(A)={\begin{cases}X_{1}&{\text{ falls }}c\in A\\\emptyset &{\text{ falls }}c\notin A\;.\end{cases}}}$

Da die Grundmenge und die leere Menge in jeder beliebigen σ-Algebra enthalten sind, sind sie insbesondere in ${\displaystyle {\mathcal {A}}_{1}}$ enthalten und die Funktion ist messbar.

• Sind ${\displaystyle (X_{1},{\mathcal {A}}_{1})}$ und ${\displaystyle (\{0,1\},{\mathcal {P}}(\{0,1\}))}$ Messräume, dann ist für beliebiges ${\displaystyle M\in {\mathcal {A}}_{1}}$ die Indikatorfunktion ${\displaystyle f=\chi _{M}}$ eine ${\displaystyle {\mathcal {A}}_{1}}$-${\displaystyle {\mathcal {P}}(\{0,1\})}$-messbare Funktion. Es gilt dann ${\displaystyle f^{-1}(\{1\})=M}$ und ${\displaystyle f^{-1}(\{0\})=X_{1}\setminus M}$ sowie ${\displaystyle f^{-1}(\emptyset )=\emptyset }$ und ${\displaystyle f^{-1}(\{0,1\})=X_{1}}$. Diese Mengen sind aber nach Voraussetzung in der σ-Algebra enthalten.

Einordnung

Urbild einer messbaren Menge

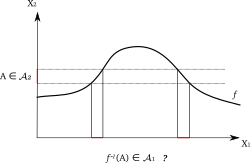
Der Begriff der Messbarkeit wird durch die Definition der Integration von Henri Lebesgue motiviert: Für die Lebesgue-Integration einer Funktion ${\displaystyle f\colon \mathbb {R} \rightarrow \mathbb {R} }$ bezüglich des Lebesgue-Maßes muss Mengen der Form ${\displaystyle f^{-1}([a,b])}$ ein Maß zugeordnet sein. Beispiele für Funktionen, für die dies nicht möglich ist, sind Indikatorfunktionen von Vitali-Mengen. Die Definition der Lebesgue-Integration für beliebige Maßräume führt dann zu obiger Definition der messbaren Funktion.

Der Begriff der messbaren Funktion hat Parallelen zur Definition der stetigen Funktion. Eine Funktion zwischen topologischen Räumen ${\displaystyle X_{1}}$ und ${\displaystyle X_{2}}$ ist genau dann stetig, wenn die Urbilder offener Mengen von ${\displaystyle X_{2}}$ wiederum offene Mengen von ${\displaystyle X_{1}}$ sind. Die von den offenen Mengen erzeugte σ-Algebra ist die borelsche σ-Algebra. Eine stetige Funktion ist also messbar bezüglich der Borel-σ-Algebren von ${\displaystyle X_{1}}$ und ${\displaystyle X_{2},}$ kurz borel-messbar. Eine gewisse Umkehrung dieser Aussage ist der Satz von Lusin.

Messbare Funktionen spielen als Zufallsvariablen eine wichtige Rolle in der Wahrscheinlichkeitstheorie.

Eigenschaften

Messbare Funktionen und Erzeugendensysteme

Oftmals ist eine σ-Algebra viel zu groß, um jede Menge aus ihr direkt angeben zu können oder das Urbild jeder Menge zu überprüfen. Die Überprüfung einer Funktion auf Messbarkeit wird aber dadurch erleichtert, dass man dies nur auf den Urbildern eines Erzeugers machen muss. Ist also ${\displaystyle {\mathcal {E}}_{2}}$ ein Erzeuger von ${\displaystyle {\mathcal {A}}_{2}}$, sprich ist ${\displaystyle \sigma ({\mathcal {E}}_{2})={\mathcal {A}}_{2}}$, so ist die Funktion ${\displaystyle f}$ genau dann messbar, wenn

${\displaystyle f^{-1}(E)\in {\mathcal {A}}_{1}}$

für alle ${\displaystyle E\in {\mathcal {E}}_{2}}$ gilt.

Daraus folgt direkt, dass stetige Funktionen zwischen topologischen Räumen, die mit der borelschen σ-Algebra versehen sind, immer messbar sind, da Urbilder offener Mengen immer offen sind. Da die borelsche σ-Algebra aber von den offenen Mengen erzeugt wird und demnach die Urbilder des Erzeugers wieder im Erzeuger liegen, folgt die Messbarkeit.

Initial-σ-Algebra

Zu jeder Abbildung ${\displaystyle f\colon X_{1}\to X_{2}}$, wobei ${\displaystyle X_{2}}$ mit der σ-Algebra ${\displaystyle {\mathcal {A}}_{2}}$ versehen ist, lässt sich eine kleinste σ-Algebra angeben, bezüglich derer die Funktion ${\displaystyle f}$ messbar ist. Diese σ-Algebra nennt man dann die Initial-σ-Algebra der Funktion und bezeichnet sie mit ${\displaystyle \sigma (f)}$ oder mit ${\displaystyle {\mathcal {I}}(f)}$. Sie lässt sich auch für beliebige Familien von Funktionen ${\displaystyle (f_{i})_{i\in I}}$ definieren. Sie ist dann die kleinste σ-Algebra, bezüglich derer alle ${\displaystyle f_{i}}$ messbar sind, und wird dann mit ${\displaystyle \sigma (f_{i}\colon i\in I)}$ oder ${\displaystyle {\mathcal {I}}(f_{i}\colon i\in I)}$ bezeichnet. Für eine einzelne Funktion ${\displaystyle f}$ ist aufgrund der Operationsstabilität des Urbildes bereits ${\displaystyle f^{-1}({\mathcal {A}}_{2})}$ die Initial-σ-Algebra.

Verkettungen messbarer Funktionen

Sind ${\displaystyle (X_{1},{\mathcal {A}}_{1})}$, ${\displaystyle (X_{2},{\mathcal {A}}_{2})}$ und ${\displaystyle (X_{3},{\mathcal {A}}_{3})}$ Messräume und ist ${\displaystyle f}$ ${\displaystyle {\mathcal {A}}_{1}}$-${\displaystyle {\mathcal {A}}_{2}}$-messbar und ${\displaystyle g}$ ${\displaystyle {\mathcal {A}}_{2}}$-${\displaystyle {\mathcal {A}}_{3}}$-messbar, so ist die Funktion ${\displaystyle h(x)=g(f(x))}$ ${\displaystyle {\mathcal {A}}_{1}}$-${\displaystyle {\mathcal {A}}_{3}}$-messbar. Unter Umständen kann auch aus der Messbarkeit von verknüpften Funktionen auf die Messbarkeit ihrer Teilfunktionen geschlossen werden: Sind ${\displaystyle f_{i}}$ Funktionen von ${\displaystyle (X_{2},{\mathcal {A}}_{2})}$ nach ${\displaystyle (X_{i},{\mathcal {A}}_{i})}$ und ist ${\displaystyle {\mathcal {A}}_{2}={\mathcal {I}}(f_{i})}$ die Initial-σ-Algebra, dann ist eine Funktion ${\displaystyle f}$ von ${\displaystyle (X_{1},{\mathcal {A}}_{1})}$ nach ${\displaystyle (X_{2},{\mathcal {A}}_{2})}$ genau dann messbar, wenn ${\displaystyle f_{i}\circ f}$ für alle ${\displaystyle i\in I}$ ${\displaystyle A_{1}}$-${\displaystyle A_{i}}$-messbar ist.

Faktorisierungslemma

Das Faktorisierungslemma ist ein maßtheoretischer Hilfssatz über die Messbarkeit von Funktionen, der bei einigen weitreichenden stochastischen Konstruktionen und Sätzen der mathematischen Statistik verwendet wird. Das Lemma wird beispielsweise bei der Konstruktion der faktorisierten bedingten Erwartung eingesetzt, die ein Schritt auf dem Weg zur regulären bedingten Verteilung ist. Das Lemma besagt: Wenn eine Abbildung

${\displaystyle f\colon \Omega _{1}\to \Omega _{2}}$

gegeben ist, dann ist die Abbildung

${\displaystyle g\colon \Omega _{1}\to {\overline {\mathbb {R} }}}$

genau dann ${\displaystyle \sigma (f)-{\mathcal {B}}({\overline {\mathbb {R} }})}$-messbar, wenn eine Funktion ${\displaystyle \varphi }$ existiert, so dass

${\displaystyle \varphi \colon (\Omega _{2},{\mathcal {A}}_{2})\to ({\overline {\mathbb {R} }},{\mathcal {B}}({\overline {\mathbb {R} }}))}$

messbar ist und

${\displaystyle g=\varphi \circ f}$

gilt. Dabei ist ${\displaystyle {\mathcal {A}}_{2}}$ eine σ-Algebra auf ${\displaystyle \Omega _{2}}$ und ${\displaystyle \sigma (f)}$ die von ${\displaystyle f}$ erzeugte σ-Algebra.

Messbarkeit reellwertiger Funktionen

Überprüfung

Für eine Abbildung ${\displaystyle f}$ von einem Messraum ${\displaystyle (X,{\mathcal {A}})}$ nach ${\displaystyle (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))}$ gilt, dass ${\displaystyle f}$ genau dann messbar ist, wenn eine der folgenden äquivalenten Bedingungen erfüllt ist

• ${\displaystyle \{f\leq a\}\in {\mathcal {A}}\;\forall a\in \mathbb {R} }$,
• ${\displaystyle \{f<a\}\in {\mathcal {A}}\;\forall a\in \mathbb {R} }$,
• ${\displaystyle \{f\geq a\}\in {\mathcal {A}}\;\forall a\in \mathbb {R} }$,
• ${\displaystyle \{f>a\}\in {\mathcal {A}}\;\forall a\in \mathbb {R} }$.

Dabei ist ${\displaystyle \{f\leq a\}}$ als Abkürzung für

${\displaystyle \{x\in X\mid f(x)\leq a\}=f^{-1}((-\infty ,a])}$

zu verstehen. Es würde auch ausreichen, wenn ${\displaystyle a}$ nur alle rationalen Zahlen durchliefe, denn die angegebenen Intervalle bilden immer ein Erzeugendensystem der borelschen σ-Algebra.

Messbare Funktionen

Die folgenden Funktionen ${\displaystyle g\colon (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))\to (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))}$ sind beispielsweise messbar:

${\displaystyle g(x)=\max(0,x)=:x^{+}}$

${\displaystyle g(x)=\min(0,x)=:x^{-}}$

${\displaystyle g(x)=|x|}$

${\displaystyle g(x)=\operatorname {sgn} (x)}$.

Ist außerdem eine Funktion ${\displaystyle f\colon (X_{1},{\mathcal {A}}_{1})\to (\mathbb {R} ^{n},{\mathcal {B}}(\mathbb {R} ^{n}))}$ gegeben, so ist sie genau dann messbar, wenn jede ihrer Komponentenfunktionen ${\displaystyle f_{i}}$ ${\displaystyle {\mathcal {A}}}$-${\displaystyle {\mathcal {B}}(\mathbb {R} )}$-messbar ist.

Sind ${\displaystyle f,g}$ messbare Funktionen von ${\displaystyle (X_{1},{\mathcal {A}}_{1})}$ nach ${\displaystyle (\mathbb {R} ^{n},{\mathcal {B}}(\mathbb {R} ^{n}))}$, so sind auch ${\displaystyle f+g}$ und ${\displaystyle f-g}$ messbar. Ist ${\displaystyle h}$ messbar von ${\displaystyle (X_{1},{\mathcal {A}}_{1})}$ nach ${\displaystyle (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))}$, so ist ${\displaystyle f\cdot h}$ messbar. Vereinbart man die Konvention ${\displaystyle {\tfrac {x}{0}}=0}$, so ist sogar ${\displaystyle {\tfrac {f}{h}}}$ messbar.

Ist eine Funktionenfolge ${\displaystyle (X_{1},{\mathcal {A}}_{1})}$-${\displaystyle ({\overline {\mathbb {R} }},{\mathcal {B}}({\overline {\mathbb {R} }}))}$-messbarer Funktionen ${\displaystyle (f_{n})_{n\in \mathbb {N} }}$ gegeben, so sind auch das Infimum, das Supremum sowie der Limes inferior und der Limes superior dieser Folge wieder messbar.

Approximation

Jede positive messbare Funktion lässt sich durch eine monoton wachsende Funktionenfolge von einfachen Funktionen (also Linearkombinationen von Indikatorfunktionen von messbaren Mengen) approximieren. Eine Funktionenfolge, die das leistet, ist beispielsweise

${\displaystyle f_{n}(x)=\min(2^{-n}\lfloor 2^{n}f(x)\rfloor ;n)}$.

Diese Approximationseigenschaft wird bei der Konstruktion des Lebesgue-Integrals genutzt, welches zuerst nur für einfache Funktionen definiert wird und dann auf alle messbaren Funktionen fortgesetzt wird.

Lebesgue- und Borelmessbare Funktionen

Eine (reelle) Lebesgue-Borel-messbare Funktion ist nicht unbedingt Borel-Borel-messbar. Auch ist eine Lebesgue-Borel-messbare Funktion nicht unbedingt Lebesgue-Lebesgue-messbar. Die Verkettung zweier Lebesgue-Borel-messbarer Funktionen ist also nicht zwangsläufig wiederum Lebesgue-Borel-messbar.^[1][2]

Verwandte Begriffe

Starke Messbarkeit

Ist eine Funktion in einem metrischen Raum punktweiser Limes von Elementarfunktionen, d. h. messbaren Funktionen mit endlichem Bild, so heißt sie „stark messbar“.

• Jede messbare Funktion mit separablem Bild ist stark messbar.
• Jede stark messbare Funktion ist messbar.

Starke Messbarkeit und Messbarkeit unterscheiden sich nur voneinander, wenn der Zielraum nicht-separabel ist. Dies ist beispielsweise bei der Definition von verallgemeinerten Integralen wie dem Bochner-Integral der Fall.

Bimessbare Funktionen

Messbare Funktionen, deren Umkehrabbildung ebenfalls messbar ist, werden bimessbare Funktionen genannt.

Abgrenzung

Eine Teilmenge eines Messraums heißt messbar, wenn sie Element der σ-Algebra des Messraums ist und ihr somit potentiell ein Maß zugeordnet werden kann. Des Weiteren existiert noch die Messbarkeit nach Carathéodory von Mengen bezüglich eines äußeren Maßes. Hier wird nur ein äußeres Maß benötigt.

Literatur

• M. Loève: Probability Theory I (= Graduate Texts in Mathematics. Band 45). 4. Auflage. Springer Verlag, New York, Heidelberg, Berlin 1977, ISBN 3-540-90210-4 (MR0651017). 
• Klaus D. Schmidt: Maß und Wahrscheinlichkeit (= Springer-Lehrbuch - Grundwissen Mathematik). Springer-Verlag, Berlin, Heidelberg 2009, ISBN 978-3-540-89729-3, doi:10.1007/978-3-540-89730-9. 
• Jürgen Elstrodt: Maß- und Integrationstheorie (= Springer-Lehrbuch - Grundwissen Mathematik). 7., korrigierte und aktualisierte Auflage. Springer-Verlag, Heidelberg, Dordrecht, London, New York 2011, ISBN 978-3-642-17904-4, doi:10.1007/978-3-642-17905-1. 
• Ehrhard Behrends: Maß- und Integrationstheorie (= Hochschultext). Springer-Verlag, Berlin, Heidelberg, New York, London, Paris, Tokyo 1987, ISBN 3-540-17850-3 (MR1028059). 
• Heinz Bauer: Maß- und Integrationstheorie (= De Gruyter Lehrbuch). 2., überarbeitete Auflage. de Gruyter, Berlin, New York 1992, ISBN 3-11-013625-2 (MR1181881). 
• Henri Lebesgue: Leçons sur l'intégration et la recherche des fonctions primitives. Gauthier-Villars, Paris 1904.
• Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6. 

Weblinks

• Eintrag meßbare Funktion im Lexikon der Mathematik (2017)
• Measurable mapping in der Encyclopedia of Mathematics
• Eintrag meßbare Abbildung im Lexikon der Mathematik (2017)

Einzelnachweise

1. ↑ Robert B. Ash, Catherine Doléans-Dade: Probability and measure theory. 2nd edition. Academic Press, San Diego CA u. a. 2000, ISBN 0-12-065202-1, S. 41.
2. ↑ Vladimir I. Bogachev: Measure theory. Band 1. Springer, Berlin u. a. 2007, ISBN 978-354-03451-3-8, S. 193.

Anmerkungen

1. ↑ Es ist also (in verkürzter Schreibung) ${\displaystyle f^{-1}{{\bigl (}{\mathcal {A}}_{2}{\bigr )}}\subseteq {\mathcal {A}}_{1}}$