Mathematisches Spiel
Mathematische Spiele, kurz: Mathespiele, sind Spiele, die abstrakt sind, abstrakt in dem Sinne, dass es dabei um nichts geht.
Allgemein
Die Spieler müssen keine Mathematiker sein, um Mathespiele zu spielen. Ihre Regeln hängen mit irgendeinem Bereich der Mathematik, der Logik oder einem bestimmten mathematischen Problem zusammen. Die Regeln sind normalerweise einfach und zählen nicht selten nur wenige, ansonsten wird das Spiel gewöhnlich nicht zu einem Mathespiel gerechnet. Brettspiele wie Schach, Go oder Mancala werden daher meist nicht als Mathespiele betrachtet. Ein Mathespiel enthält normalerweise keine Zufallsmomente. Auch einige Puzzlespiele werden zu den Mathespielen gezählt. Mathematische Rätsel erfordern die Einbeziehung der Mathematik, um eine Lösung zu erhalten. Beispiele für Mathespiele sind das Nim-Spiel, Käsekästchen, Pentomino, Türme von Hanoi, Solitär und Pentago.
Themen
Das Thema der Mathematik von Spielen ist ernster, als es vermuten lässt. Die Spieltheorie beispielsweise hat Anwendungen in sozialen und militärischen Bereichen des Studierens von Taktiken und Strategien.
Beispiele
Mathematical Games („Mathematische Spiele“) war der Titel einer Kolumne von Martin Gardner (1914–2010) im Scientific American-Magazin, die von mehreren Generationen von Mathematikern und Wissenschaftlern gelesen wurde. Douglas Hofstadter und Ian Stewart übernahmen nacheinander die Kolumnen Metamagical Themas und Mathematical Recreations.
Eine größere Sammlung bekannter mathematischer Spiele hat im deutschsprachigen Raum der Rostocker Mathematiker Wilhelm Ahrens (1872–1927) zusammengetragen. Der Göttinger Mathematiker und Naturforscher Georg Christoph Lichtenberg (1742–1799) hatte bereits 1770 einen Aufsatz Betrachtungen über einige Methoden, eine gewisse Schwierigkeit in der Wahrscheinlichkeit beim Spiel zu heben veröffentlicht.
Internationales Komitee für mathematische Spiele (FR)
In Frankreich gibt es ein Comité international des jeux mathématiques (CIJM) (übersetzt: Internationales Komitee für mathematische Spiele) mit Sitz in Paris.
Bereits im frühen 17. Jahrhundert hatte dort der Mathematiker Claude Gaspard Bachet de Méziriac (1581–1638) die Sammlung Problèmes plaisans et délectables, qui se font par les nombres (übersetzt: Angenehme und erfreuliche Probleme, die durch Zahlen entstehen) zusammengetragen (siehe auch Bachet’sches Spiel).
Der Mathematiker Édouard Lucas (1842–1891) machte im 19. Jahrhundert viele Spiele mit mathematischer Grundlage bekannt.
Literatur
- Claude Gaspard Bachet de Méziriac: Problèmes plaisans et delectables, qui se font par les nombres: Partie recueillis de diuers autheurs, & inuentez de nouueau auec leur demonstration. Tres-vtiles pour toutes sortes de personnes curieuses, qui se seruent d’Arithmetique. Pierre Rigaud, Lyon 1612; archive.org
- Wilhelm Ahrens: Mathematische Spiele. Herausgegeben von Heinrich Hemme. Die Originalausgabe dieses Buches erschien 1907 bei Teubner in Leipzig. "Der vorliegende Band folgt der fünften, unveränderten Auflage, Leipzig und Berlin 1927". Anaconda Verlag, Köln 2018 (Vorwort (PDF) )
- Martin Gardner: Mathematische Zaubereien: 115 Karten-, Würfel- und Münztricks; mathematische Spiele und Zauberkunststücke. Mit einem Vorw. von Alexander Adrion. Aus dem Amerikan. von Matthias Schramm. DuMont-Literatur-und-Kunst-Verl., Köln, 2004
- Wilhelm Ahrens: Mathematische Unterhaltungen und Spiele. Teubner, Leipzig 1901 (Digitalisat), 2. Auflage 1910–1918 in 2 Bänden (Digitalisate: I (3. A., 1921) II (2. A., 1918))
- Gerhard Kowalewski: Alte und neue mathematische Spiele. Eine Einführung in die Unterhaltungsmathematik. Mit 104 Abbildungen und Anleitungen zur Herstellung des Spielgeräts. Teubner, 1930
- Bruno Kerst: Mathematische Spiele. Grote’sche Verlagsbuchhandlung, 1933
. 2. Auflage 1624.
- Alexander Petrowitsch Domorjad (russisch Александр Петрович Доморяд, wiss. Transliteration Aleksandr Petrovič Domorjad): Математические игры и развлечения [Mathematische Spiele und Unterhaltung]. Staatsverlag für physikalisch-mathematische Literatur, Moskau 1961 (Online-Teilansicht) (russisch)
- W. W. Rouse Ball: Mathematical Recreations and Essays, 1. Auflage 1892 (Digitalisat, Sixth edition)
- Guo Kaisheng郭凯声: Shuxue youxi数学游戏 [Mathematisches Spiele]. Kexue jishu wenxian chubanshe科学技术文献出版社, 1999. ISBN 978-7-5023-3427-7 (2 Teile) (chinesisch)
- Édouard Lucas: Récréations mathématiques (4 Bände), Gauthier-Villars, Paris 1882–1894 (französisch; Band 1 unter anderem über Labyrinthe; im Internet-Archiv: Band 1, 1, 2, 2, 3, 3, 3, 3, 4, 4, 4, 2. Auflage Band 1, 1, 2)
- Nikolai Nikandrowitsch Petrow (russisch Николай Никандрович Петров, wiss. Transliteration Nikolaj Nikandrovič Petrov): Математические игры [Mathematische Spiele]. 2011
- Georg Christoph Lichtenberg: Betrachtungen über einige Methoden, eine gewisse Schwierigkeit in der Berechnung der Wahrscheinlichkeit beym Spiel zu heben. Göttingen 1770 (Digitalisat)
Weblinks
- Nicht nur zum Zündeln … Streichhölzer im Dienste des Physiklernens (PDF; 221 kB)
- Didier Faradji: Qu’est-ce qu’un jeu mathématique? (PDF; 379 kB)
- Historical Math Problems/Puzzles – Mathematical Association of America Convergence
- Math games help students learn
- Jochen Werner: Merkwürdige Mathematik (PDF; 2,6 MB)
Auf dieser Seite verwendete Medien
Autor/Urheber: Schnark, Lizenz: CC0
Graph für das Problem von Wolf, Ziege und Kohlkopf
(c) Matemateca (IME USP) / (name of the photographer), CC BY-SA 4.0
Clumsy wagon, a puzzle that has as its core a mathematical problem that seeks to verify if it is possible for a wagon with only two points of contant to pass through a winding rail, available on the collection of Matemateca IME-USP
Autor/Urheber: Preambulist, Lizenz: CC0
Trihexaflexagon in the process of unfolding. Trihexaflexagon is the simplest kind of flexagon. It is a hexagon glued from a strip of paper. It is able to flex, revealing new surfaces, but without changing its shape.
Autor/Urheber: Uncopy, Lizenz: CC BY-SA 3.0
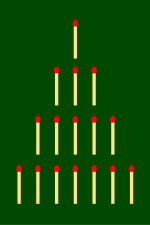
Schema einer Ausgangsstellung für Nim mit Streichhölzern
Autor/Urheber:
André Karwath aka Aka
, Lizenz: CC BY-SA 2.5Diese Animation zeigt die Lösung des Spiels "Türme von Hanoi" mit drei Scheiben. Es gibt auch eine Version mit vier Scheiben.