Mathematisches Pendel

Das mathematische Pendel oder ebene Pendel ist ein idealisiertes Pendel. Hierbei kann eine als punktförmig gedachte Masse, die mittels einer masselosen Pendelstange an einem Punkt aufgehängt ist, in einer vertikalen Ebene hin und her schwingen, wobei Reibungseffekte, insbesondere der Luftwiderstand vernachlässigt werden. Das ebene Pendel ist ein Spezialfall des Kugelpendels, das sich auch in andere Raumrichtungen bewegen kann. Da die Bewegung des Pendelkörpers auf einem vertikalen Kreis erfolgt, wird es auch als Kreispendel[1] bezeichnet, obwohl damit häufiger das Kegelpendel gemeint ist.
In der Praxis kann man ein mathematisches Pendel dadurch annähern, dass man einen möglichst langen und dünnen Stab oder (falls die Auslenkung kleiner als 90° ist) einen dünnen Faden und einen möglichst kleinen und schweren Pendelkörper verwendet. Dass bei diesem Aufbau die Schwingungsweite (Amplitude) erst nach einer großen Anzahl Schwingungen spürbar zurückgeht, zeigt, dass hierbei die Reibung nur einen geringen Einfluss hat.
Pendel, welche die genannten Eigenschaften des mathematischen Pendels nicht nähererungsweise erfüllen, lassen sich durch das kompliziertere Modell des physikalischen Pendels beschreiben.
Die Schwingungsdauer ist unabhängig von der Masse des schwingenden Körpers. Bei kleinen Schwingungen ist die Schwingungsdauer auch nahezu unabhängig von der Größe der Amplitude. Hier zeigt das Pendel eine nahezu harmonische Schwingung, deren Schwingungsdauer ausschließlich von der Länge des Pendels und der herrschenden Schwerebeschleunigung bestimmt wird. Die Schwingungsdauer verlängert sich bis ins Unendliche, je näher die Amplitude an 180° herankommt. Wenn die Bewegungsenergie genau so groß ist, dass der Punkt für das obere instabile Gleichgewicht erreicht werden kann, dann vergeht ohne Reibungseffekte eine unendlich lange Zeit bis zum Stillstand. Wenn die Bewegungsenergie größer ist, bewegt sich der Pendelkörper periodisch im Kreis.
Mathematische Beschreibung
Bewegungsgleichung

Anhand der Kräfte wird im Folgenden die Bewegungsgleichung der Pendelschwingung aufgestellt.
Aufgrund der Schwerkraft (, = Schwerebeschleunigung) ergibt sich bei Auslenkung eines Fadenpendels der Masse eine Kraft , die tangential zur kreisförmigen Pendelbahn wirkt. Die radiale Komponente spielt für die Bewegung keine Rolle, da sie in Richtung des Fadens wirkt. Da das mathematische Pendel nur einen Freiheitsgrad besitzt, genügt eine skalare Gleichung. Der Betrag der Rückstellkraft steigt mit dem Auslenkungswinkel bezüglich der Ruhelage. Hierbei zeigt der Vektor der Rückstellkraft immer in Richtung der Ruheposition, daher ergibt sich ein Minus in folgender Gleichung:
Beim Betrachten eines schwingenden Fadenpendels zeigt sich, dass die Geschwindigkeit mit zunehmender Auslenkung abnimmt und nach Erreichen des Scheitelpunkts die Richtung wechselt. Die Geschwindigkeitsänderung bedeutet, dass die Pendelmasse eine Beschleunigung erfährt, genauer gesagt findet eine Tangentialbeschleunigung statt, da eine kreisförmige Bewegungsbahn vorliegt. Die Bewegungsgleichung lautet nach dem 2. Newtonschen Gesetz:
Die Tangentialbeschleunigung lässt sich durch die Winkelbeschleunigung ausdrücken.
Bei der ungestörten Schwingung stellt die Rückstellkraft des Pendels die einzige äußere Kraft dar. Nach Umstellen und Kürzen der Masse entsteht eine nichtlineare Differentialgleichung zweiter Ordnung:
die sich mit Hilfe der Winkelgeschwindigkeit auch als System von zwei gekoppelten Differentialgleichungen erster Ordnung schreiben lässt:
- ,
- .
Bewegungsgleichung in kartesischen Koordinaten
Neben der Bewegungsgleichung mit dem Winkel existieren weitere mögliche Beschreibungsformen. So lässt sich die Bewegung des mathematischen Pendels auch als Vektordifferentialgleichung mit kartesischen Koordinaten formulieren. Eine mögliche Herleitung erfolgt über den Lagrange-Formalismus mit Lagrange-Multiplikator. Die holonome Zwangsbedingung findet sich dabei mit dem Gedanken, dass die Länge des Pendelarms der Länge des Ortsvektors entspricht. Da die Länge des Pendelarms beim mathematischen Pendel konstant ist, muss folglich gelten:
Anhand dieser holonomen Zwangsbedingung findet sich die unten stehende Vektordifferentialgleichung. Dabei stellt der erste Term die Zentripetalbeschleunigung und der zweite Term den an die Kreisbahn tangentiell wirkende Anteil der Schwerebeschleunigung dar. In dieser Darstellung entfällt die Länge des Pendelarmes in der Differentialgleichung. Allerdings wird durch die Anfangswerte definiert, welche sich in Abhängigkeit von den Anfangswerten des Winkels und der Winkelgeschwindigkeit darstellen lassen.
Kleine Amplituden: Harmonische Schwingung

Für kleine Winkel gilt die Kleinwinkelnäherung:
- .
Durch Substitution ergibt sich somit eine lineare Differentialgleichung zweiter Ordnung
- ,
welche der allgemeinen Form entspricht und somit deren allgemeine Lösung die Form besitzt. Daraus folgt für die Schwingungsgleichung:
Hierbei bezeichnen die Winkelamplitude und den Nullphasenwinkel zum Zeitpunkt . Darüber hinaus sind die Eigenkreisfrequenz und die zugehörige Periodendauer ersichtlich.
Exakte Lösung

Da Pendel in der Realität immer mehr als infinitesimal ausgelenkt werden, verhalten sie sich nichtlinear, d. h., Schwingungen mit endlicher Amplitude sind anharmonisch. Die Lösung der allgemeinen Differentialgleichung erfordert den Einsatz elliptischer Funktionen und elliptischer Integrale.
Gegeben ist die Differentialgleichung
- .
Diese kann mittels der jacobischen elliptischen Funktionen und gelöst werden. Die erhaltenen Formeln für Phase, Winkelgeschwindigkeit und -beschleunigung des Pendels lauten:
- ,
- ,
Der maximale Ausschlagswinkel liegt unterhalb von .
Die Periode der Pendelschwingung ergibt sich aus der Periodizität der Funktion . So führt
zu
- .
Damit lässt sich die allgemeine Lösung für die Periode in eine Reihe entwickeln:
Alternativ lässt sich das auftretende elliptische Integral auch über das arithmetisch-geometrische Mittel auswerten:
Außerdem ist die Dämpfung durch Reibungsverluste bei einem echten Pendel größer als null, so dass die Auslenkungen ungefähr exponentiell mit der Zeit abnehmen.
Dass die Periodendauer nicht von , sondern nur von dem Verhältnis abhängt, lässt sich auch aus einer Dimensionsanalyse, z. B. mit dem buckinghamschen Π-Theorem, herleiten. Nur der numerische Faktor ( bei kleinen Amplituden, in der exakten Lösung) ist so nicht zu ermitteln.
Der Winkel als explizite Funktion der Zeit mit Startwinkel und (positiver) Startgeschwindigkeit lautet
mit , wobei die Jacobi-Amplitude und das elliptische Integral erster Art ist (hier sind die elliptischen Module in Mathematica-Konvention bereits quadriert angegeben). Bei negativem kann die Situation einfach gespiegelt werden, indem das Vorzeichen des Startwinkels vertauscht wird.[2] Mit und kleinen Werten von (auf dem Hauptzweig der Jacobi-Amplitude) ist dieser Ausdruck dem äquivalent, das mithilfe des Arcustangens und der Jacobi-cn-Funktion berechnet wurde (s. o.).
Numerische Lösung
Durch numerische Integration der beiden Differentialgleichungen 1. Ordnung lässt sich eine Näherungslösung rekursiv berechnen. Mit dem einfachsten Integrationsverfahren (Euler explizit) und der Schrittweite ergibt sich für die Winkelgeschwindigkeit:
Für den Winkel kann die zuvor berechnete Winkelgeschwindigkeit benutzt werden:
Die Anfangswerte für Winkelgeschwindigkeit und Winkel sind dem Index zugeordnet.
Die Genauigkeit der Lösung lässt sich durch Simulation über mehrere Perioden und Anpassung der Schrittweite überprüfen. Dieses Verfahren ist in der Physik auch als Methode der kleinen Schritte bekannt.
Erhaltungssätze
Beim mathematischen Pendel gilt der Energieerhaltungssatz der Mechanik. Auf dem Weg von der maximalen Auslenkung zur Ruhelage nimmt die potentielle Energie ab. Die mit ihr verbundene Gewichtskraft – genauer: deren tangentiale Komponente – verrichtet Beschleunigungsarbeit, wodurch die kinetische Energie zunimmt. Nach Durchschreiten des Minimums wirkt eine Komponente der Gewichtskraft entgegen der Bewegungsrichtung. Es wird Hubarbeit verrichtet.
Auch hieraus lässt sich die Differentialgleichung herleiten:
Die Summe ist zeitlich konstant, also
Diese Gleichung hat zwei Lösungen:
- , es gibt keine Bewegung; diese Lösung kann man hier unbeachtet lassen.
- ; diese Lösung stimmt mit der Lösung oben überein.
Anhand der Energieerhaltung kann die maximale Geschwindigkeit der Pendelmasse nach Loslassen beim Winkel berechnet werden:
Die maximale Geschwindigkeit wird im tiefsten Punkt der Pendelmasse erreicht, d. h. wenn der Faden senkrecht ist.
Gleichgewichtspunkte im Phasenraum
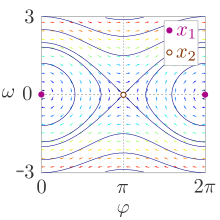
Der Zustand des Systems lässt sich durch einen Punkt im Phasenraum, d. h. durch ein Tupel aus dem Winkel und der Winkelgeschwindigkeit beschreiben.
Es gibt zwei Positionen und , bei dem sich das System in einem mechanischen Gleichgewicht befindet. In beiden Punkten ist die Winkelgeschwindigkeit und die Summe aller angreifenden Kräfte und Momente Null. Der Gleichgewichtspunkt bei einem Winkel von Null ist das stabile Gleichgewicht, wenn das Pendel keine Auslenkung und Geschwindigkeit besitzt. Der zweite Punkt ist das instabile Gleichgewicht, wenn das Pendel keine Geschwindigkeit besitzt und „auf dem Kopf“ steht.
Literatur
- Ekbert Hering, Rolf Martin, Martin Stohrer: Physik für Ingenieure. 8. Auflage. Springer, Berlin Heidelberg New York 2002, ISBN 3-540-42964-6.
Weblinks
- A comprehensive analytical solution of the nonlinear pendulum, Karlheinz Ochs
Einzelnachweise
- ↑ Physik und Mathematik mit Maple, Kreispendel, abgerufen am 22. Dezember 2014
- ↑ Simon Tyran: Der Winkel eines Pendels als explizite Funktion der Zeit. 2016, S. 3, abgerufen am 4. April 2016.
Auf dieser Seite verwendete Medien
Autor/Urheber: Stephan Kulla (User:Stephan Kulla), Lizenz: CC0
Diagram showing the small-angle approximation of the sine function.
Autor/Urheber: Alessio Damato; thanks to John wayman, he let me notice a mistake in the code., Lizenz: CC BY-SA 3.0
A plot of the ratio between the actual period of a pendulum and the approximate value obtained for small angles, as a function of the amplitude. According to Pendulum (mathematics), the oscillation period for small angles is given by:
while the actual period for any angle is given by:
where:
so the ratio is given by:
and this is the function plotted in the graph. First, with the following Matlab code I created a file called pendulum_period.dat;
then, in order to plot it, I used the Gnuplot code.
This code creates a file called pendulum_period.svg. I heavily post-processed it with Inkscape.









