Mathematica
| Wolfram Mathematica | |
|---|---|
 | |
 | |
| Basisdaten | |
| Entwickler | Wolfram Research |
| Erscheinungsjahr | 1988 |
| Aktuelle Version | 14.2[1] (23. Januar 2025) |
| Betriebssystem | Windows, MacOS, Linux, 64-bit-Implementierungen |
| Programmiersprache | C, C++[2], Java[2], Wolfram Language |
| Kategorie | Computeralgebrasystem, Informationsvisualisierung, Statistik-Software, Grafische Benutzeroberfläche |
| Lizenz | Proprietäre Software |
| wolfram.com/products/mathematica | |
Mathematica ist eines der meistbenutzten mathematisch-naturwissenschaftlichen Programmpakete und ein proprietäres Softwarepaket des Unternehmens Wolfram Research. Mathematica 1.0 wurde 1988 auf den Markt gebracht.
Programmpaket Mathematica
Das Softwarepaket Mathematica enthält unter anderem
- ein Computeralgebrasystem zur symbolischen Verarbeitung von Gleichungen und Differentialgleichungen.[3][4]
- eine Numerik-Software zum numerischen Lösen oder Auswerten von Gleichungen
- ein Visualisierungs-Tool zum Darstellen von Graphen und 3D/2D Graphiken
- eine Programmiersprache, die Elemente des prozeduralen, objektorientierten, funktionalen und regelbasierten Programmierens in sich vereint.
Der Autor und Unternehmensbegründer Stephen Wolfram begann die Entwicklungsarbeit im Jahr 1986, die erste Version von Mathematica wurde 1988 herausgebracht. Der Name Mathematica wurde Wolfram zufolge von Steve Jobs vorgeschlagen.[5][6]
Mathematica 1.0 enthielt über 500 eingebaute Funktionen, die in Mathematica 14.0 weiterhin vorhanden sind. In der Version 4.0 aus dem Jahr 2000 waren es über 1000 Funktionen. Diese sind in einem gedruckten Handbuch, das über 3 kg wiegt, auf fast 1500 Seiten dokumentiert.[7] In der Version 14.1 aus dem Jahr 2024 sind es über 6600 Funktionen. Ein gedrucktes Handbuch wird nicht mehr angeboten.[8] Hinzu gekommen ist außerdem eine große Anzahl neuer Ideen, die den Einsatzbereich des Systems erweitern. Mit dem Wolfram Function Repository gibt es seit 2019 eine Möglichkeit für die Wolfram-Community, öffentliche Standalone-Funktionen zur Wolfram Language beizutragen, die sofort in dieser einsetzbar sind.[9]
Benutzung und Arbeitsmethode

Mathematica besteht aus dem Kernel, der die Berechnungen vornimmt, sowie dem Notebook, einer grafischen Benutzeroberfläche. Das Programm wird in der Regel über das Notebook bedient, das die Ein- und Ausgabe formatiert darstellt. Das Notebook hat außerdem Funktionen einer Textverarbeitung und erlaubt das Darstellen und Manipulieren von Grafiken. Ein besonderes Merkmal ist auch die umfangreiche Unterstützung mathematischer Sonderzeichen, die in Mathematica (im Gegensatz zu klassischen Programmiersprachen) an jeder Stelle (auch als Variablennamen) genutzt werden können.
Der Kernel interpretiert den Programmcode in der Regel gleich nach der Eingabe, Ergebnisse oder Programmierfehler sind damit sofort zu sehen, das Programmieren ist interaktiv. Wird Programmcode mehrfach durchlaufen, etwa beim nicht-interaktiven Programmaufruf, so wird der Programmcode automatisch kompiliert. Der Programmcode ist betriebssystemunabhängig. Mathematica wird angeboten für Windows, Linux und macOS, bis einschließlich Version 6.0.3 auch für MS-DOS, NeXT, OS/2, Unix und VMS.
Ab Version 8 ist der sogenannte free form input in Mathematica verfügbar, der es ermöglicht, anstatt der Eingabe der korrekten Syntax für Berechnungen und andere Befehle, „natürliches“ Englisch zu verwenden. Dafür ist allerdings eine Internetverbindung nötig. So wird beispielsweise das gleiche Ergebnis – der Graph der Sinusfunktion mit hellroter Füllung und gestrichelten Linien – erzielt, wenn man
Plot[Sin[x], {x, -6.6, 6.6},
Filling -> Axis,
FillingStyle -> Lighter[Red],
GridLines -> Automatic,
GridLinesStyle -> Dashed
]
eingibt, wie aber auch den free form input verwendend
plot sin x with light red filling and dashed grid lines
als Befehl nimmt. Nachdem man einen mit free form input vorgenommenen Befehl getätigt hat, kann man ihn in die genaue Syntax übersetzen lassen und dann wieder verändern, sodass Kenntnis über die Syntax dennoch von Vorteil bleibt.[10][11]
Mathematica wird in der Wissenschaft beziehungsweise im Studium natur- oder wirtschaftswissenschaftlicher Fächer eingesetzt. Ebenso wendet es sich an den professionellen Anwender in der Industrie und Wirtschaft. So verwenden Banken Mathematica zur Simulation von Aktienkursentwicklung, Bewertung von Derivaten, Risikoabschätzung und -wandlung und so weiter. Die Anforderung an die Korrektheit der Ergebnisse (analytisch wie numerisch) ist daher hoch.
Neben den Grundrechenarten, Ableitungs- und Integralberechnung, Lösen von Gleichungssystemen, Matrizenmanipulation und numerischen Berechnungen in beliebiger Genauigkeit (keine Beschränkung auf die Maschinenpräzision) sind eine Vielzahl spezieller Funktionen, etwa aus den Bereichen der Kombinatorik, implementiert. Die Programmiersprache von Mathematica umfasst implizite Typenzuweisung und -wandlung, automatisches Speichermanagement und Musterauswertungstechniken (englisch pattern matching). Mathematica hat integrierten Zugriff auf die riesige Wolfram Knowledgebase, die auch Wolfram Alpha antreibt und aktuelle Daten aus der realen Welt in Tausenden von Bereichen enthält.[12] Seit Ende 2013 wird die Programmiersprache Wolfram Language unabhängig von Mathematica vertrieben.[13]
Zu den Alternativen zum Mathematica-Frontend gehört Wolfram Workbench – eine Eclipse-basierte integrierte Entwicklungsumgebung (IDE), die 2006 eingeführt wurde. Sie bietet projektbasierte Code-Entwicklungstools für Mathematica, einschließlich Revisionsmanagement, Debugging, Profiling und Testen. Es gibt auch ein Plugin für IntelliJ-IDEA-basierte IDEs zur Arbeit mit Wolfram Language-Code, das zusätzlich zur Syntaxhervorhebung lokale Variablen und definierte Funktionen analysieren und automatisch vervollständigen kann. Der Mathematica-Kernel enthält auch ein Kommandozeilen-Frontend.
Sprache
Die Programmiersprache von Mathematica (Wolfram Language)[14] ist stark an die funktionale Programmiersprache Lisp angelehnt. Zusätzlich basiert Mathematica wesentlich auf Pattern Matching (wie zum Beispiel auch Haskell). Dies sorgt besonders bei Einsteigern für Verwirrung, weil Patterns, also Muster-Platzhalter, vorkommen, sobald man mit Funktionen arbeitet. Zusammen mit den fast ständig genutzten eckigen Klammern entsteht so ein Code-Aussehen, das sich stark von den verbreiteten C-artigen Programmiersprachen unterscheidet. Bei folgender Definition handelt es sich für Mathematica nicht um eine Funktion, sondern um eine Ersetzungsregel, bei der jedes Vorkommen von f[irgendwas] durch irgendwas + irgendwas ersetzt wird, wobei irgendwas sprichwörtlich alles sein kann:
f[x_] = x + x
Eine wirkliche Funktion im Sinne der funktionalen Programmierung/des Lambda-Kalküls wird hingegen durch Function erzeugt: f = Function[x, x + x]
Der Vorteil des Pattern-Matching in der Computeralgebra liegt darin, dass man komplizierte Ersetzungsregeln kompakt schreiben kann. Eine abschnittsweise definierte Funktion könnte man über Matching-Regeln wie folgt definieren:
g[x_ /; x < 7] = 2*x; g[x_ /; x > 7] = 3*x;
Aufrufe g[3] werden damit als 2*3=6 ausgewertet, wohingegen g[10] die Auswertung 3*10=30 ergibt.

Plus[a,Sin[Times[b,c]]] als TreeFormWie Lisp weist Mathematica die Eigenschaft der Homoikonizität auf. Das bedeutet, dass Mathematica-Code und das Ergebnis einer Berechnung aus demselben Typ Daten besteht. Mathematica-Anweisungen wie -Ausgaben sind eigentlich Bäume, und eine Auswertung einer Eingabe besteht in der Transformation eines solchen Baumes. Aus diesem Grund nennt man das erste Element eines Mathematica-Ausdruckes auch Head, im folgenden Beispiel ist der Head die Anweisung Plus:
Plus[a,Sin[Times[b,c]]]
Als Baum dargestellt sieht dieser Ausdruck wie rechts gezeigt aus. Der Head (also Wurzelknoten) des Baumes ist die Funktion Plus. Mathematica kennt verschiedene Weisen, Ein/Ausgaben darzustellen. In natürlicher Schreibweise entspricht dieser Ausdruck dem besser lesbaren a + Sin[b*c]
Mathematica unterstützt als Computeralgebrasystem die Verarbeitung beliebiger Symbole in derartigen Ausdrücken. Anhand von einer Liste von Ersetzungsregeln werden diese Ausdrücke zu anderen Bäumen umgeformt. So zusammengebaut sind komplexe Rechnungen möglich. Mathematica ist damit dynamisch typisiert. Im Gegensatz zu anderen Sprachen ist bei Mathematica damit eine nicht auswertbare Zeile im Allgemeinen kein Fehler, sondern verbleibt unverändert als Rückgabe. Fehlerausgaben sind aber dennoch möglich, zum Beispiel bei Übergabe ungeeigneter Argumente an eine (eingebaute) Funktion wie Plot.
Der Programmierer ist nicht auf ein einziges Programmierparadigma festgelegt, sondern kann ebenso imperative Anweisungen programmieren. Durch zehntausende von eingebauten Funktionen kann man sehr schnell umfangreiche Programme schreiben.
Sprachbeispiele
Beispiel 1: Primzahlen
Mit der Funktion Prime[k] wird die k-te Primzahl berechnet und angezeigt, zum Beispiel
- In[1]:=
Prime[15]- Out[1]=
47 - Out[1]=
Man beachte: Präfixe werden von Mathematica in kleiner Schrift und in bläulicher Farbe ausgeschrieben (sind also keine Links).
Eine Liste von Primzahlen kann auf mehrere Arten erzeugt werden, zum Beispiel die Liste der ersten 15 Primzahlen.
1. Variante: Die Funktion Table anwenden
- In[1]:=
Table[Prime[i],{i,15}]- Out[1]=
{2,3,5,7,11,13,17,19,23,29,31,37,41,43,47} - Out[1]=
2. Variante: Die Funktion Range anwenden
- In[1]:=
Prime /@ Range[15]- Out[1]=
{2,3,5,7,11,13,17,19,23,29,31,37,41,43,47} - Out[1]=
3. Variante: Primzahlen in Datenfeldern speichern
- In[1]:=
f[n_]:=Table[Prime[i],{i,n}]- In[2]:=
f[15]- Out[2]=
{2,3,5,7,11,13,17,19,23,29,31,37,41,43,47} - In[2]:=
4. Variante: Die Liste der Primzahlen blockweise über Primzahlstufen selektieren
- In[1]:=
tm = 2; p = {}; k = 1; Do[
Do[If[t > 0,
For[i = 1, (s = p[[i]]) <= t + 1, i++,
If[GCD[k - s, 2 s - 1] != 1, Goto[l]]]]; p = AppendTo[p, k];
Label[l]; k++, {4 (t + 1)}], {t, 0, tm}]; p *= 2; p--; p[[1]]++; p
- Out[1]=
{2,3,5,7,11,13,17,19,23,29,31,37,41,43,47}
Die 4. Variante vermittelt einen Eindruck von Mathematica als Programmiersprache.
Es gibt weitere Primzahl-Funktionen. Die Funktion PrimePi[x] gibt die Anzahl der Primzahlen kleiner oder gleich x zurück, zum Beispiel
- In[1]:=
PrimePi[50]- Out[1}=
15 - Out[1}=
Ob die Ganzzahl n eine Primzahl ist, kann man mit der Funktion PrimeQ[n] abfragen. Zum Beispiel: Ist die Jahreszahl 2017 eine Primzahl?
- n[1]:=
PrimeQ[2017]- Out[1]=
True - Out[1]=
Ist die Jahreszahl 2023 eine Primzahl?
- In[1]:=
PrimeQ[2023]- Out[1]=
False - Out[1]=
Welche Teiler hat 2023?
- In[1]:=
Divisors[2023]- Out[1]=
{1,7,17,119,289,2023} - Out[1]=
Beispiel 2: Mittelwertberechnung
Untenstehend drei Arten, mit Mathematica den Mittelwert einer Werteliste zu berechnen. Im interaktiven Modus nummeriert Mathematica die Ein- und Ausgaben und liefert die Ergebnisse direkt.
Werteliste definieren:
- In[1]:=
myData = Range[8]- Out[1]=
{1, 2, 3, 4, 5, 6, 7, 8} - Out[1]=
Mathematica-eigene Funktion benutzen:
- In[2]:=
Mean[myData]- Out[2]=
9/2 - Out[2]=
Listenmanipulation benutzen:
- In[3]:=
Plus@@myData / Length[myData]- Out[3]=
9/2 - Out[3]=
Prozedurales Vorgehen:
- In[4]:=
summe = 0- Out[4]=
0- In[5]:=
For[ j=1,j <= Length[myData], j++, summe += myData[[j]] ]- In[6]:=
summe / Length[myData]- Out[6]=
9/2 - Out[4]=
Beispiel 3: Matrizen
Mathematica enthält eine Vielzahl von Funktionen, um Matrizen zu erzeugen, etwa eine Hilbert-Matrix oder eine Hankel-Matrix, und solche, um Matrizen zu manipulieren. Die Matrixelemente können sowohl Zahlen als auch Symbole sein. Verwenden wir im nachfolgenden Beispiel Symbole und geben der Matrix den Namen FeldX. Die Matrixelemente werden in einer speziellen Syntax Zeile für Zeile eingegeben. Mit der Funktion MatrixForm wird die Matrix in der üblichen Form angezeigt:
- In[1]:=
MatrixForm [FeldX={{a, b, 0}, {c, a, b}, {0, c, a}}]- Out[1]//MatrixForm=
- Out[1]//MatrixForm=

Diese Matrix ist eine Tridiagonal-Toeplitz-Matrix. Für die Matrizenmultiplikation wird zwischen die Feldnamen ein schlichter Punkt (.) gesetzt.[15] Zum Beispiel für die Multiplikation des Felds FeldX mit sich selbst sieht die Syntax so aus:
- In[2]:=
MatrixForm [FeldX.FeldX]- Out[2]//MatrixForm=
- Out[2]//MatrixForm=
Die Transponierte der Matrix FeldX erzeugt man so:
- In[3]:=
MatrixForm [Transpose[FeldX]]- Out[3]//MatrixForm=
- Out[3]//MatrixForm=
Die Determinante der Matrix wird mit der Funktion Det[FeldX] berechnet:
- In[4]:=
Det[FeldX]- Out[4]=
a³-2abc - Out[4]=
Die Inverse der Matrix FeldX erhält man mit der Funktion Inverse[FeldX]:
- In[5]:=
MatrixForm [Inverse[FeldX]]- Out[5]//MatrixForm=
Die Eigenwerte werden mit der Funktion Eigenvalues[FeldX] berechnet:
- In[6]:=
Eigenvalues[FeldX]- Out[6]=
{a, a – , } - Out[6]=
Sind a, b und c reell und die Vorzeichen von a und b unterschiedlich, sind zwei Eigenwerte komplex und sie sind konjugiert komplex. Analog können die Eigenvektoren mit der Funktion Eigenvectors[FeldX] berechnet werden.
Beispiel 4: Platonische Körper zeichnen

Platonische Körper sind Polyeder, die von mehreren deckungsgleichen ebenen regelmäßigen Vielecken begrenzt werden. Andere Namen sind reguläre Körper oder reguläre Polyeder. Es gibt fünf solche regulären Körper (Tetraeder, Würfel, Oktaeder, Dodekaeder, Ikosaeder). Um diese zu zeichnen, enthält Mathematica die Funktion Polyhedron.[17] Als Argument (Option) ist der englische Name des Polyeders anzugeben. Es gibt weitere verwandte Funktionen, zum Beispiel die Funktion Truncate, die einen Polyederstumpf (Tetraederstumpf, Hexaederstumpf, Oktaederstumpf, Dodekaederstumpf, Ikosaederstumpf) zeichnet, der durch Abschneiden der Ecken entsteht.
Vor Eingabe der ersten Funktion muss das Paket Polyheda geladen werden.
- In[1]:=
<< Graphics`Polyhedra`- In[2]:=
Show[Polyhedron[Tetrahedron]] - In[2]:=
Dann können nacheinander die anderen regulären Polyeder und ihre Stümpfe gezeichnet werden, die die Grafik zeigt.
Show[Polyhedron[Cube]] Show[Polyhedron[Octahedron]] Show[Polyhedron[Dodecahedron]] Show[Polyhedron[Icosahedron]] Show[Truncate[Polyhedron[Tetrahedron]]] Show[Truncate[Polyhedron[Cube]]] Show[Truncate[Polyhedron[Octahedron]]] Show[Truncate[Polyhedron[Dodecahedron]]] Show[Truncate[Polyhedron[Icosahedron]]]
In diesem Fall ist die Anwendung von Mathematica sehr einfach. Für dieses Beispiel wurde die Version 3.0 (1996) von Mathematica verwendet. Ab der Version 12.0 (2019) ist die Syntax der Funktion Polyhedron geändert worden.[18]
Versionsgeschichte
Die Entwicklung von Mathematica von Version zu Version ist so dynamisch, dass es unmöglich erscheint, die Neuerungen, und seien es auch nur die wichtigsten, tabellarisch zu erfassen. Eine Übersicht kann man sich auf der Web-Seite Mathematicas kurze Versionsgeschichte verschaffen.[19]
| Version | Veröffentlichung |
|---|---|
| 1.0 | 23. Juni 1988 |
| 1.1 | 31. Oktober 1988 |
| 1.2 | 1. August 1989 |
| 2.0 | 15. Januar 1991 |
| 2.1 | 15. Juni 1992 |
| 2.2 | 1. Juni 1993 |
| 3.0 | 3. September 1996 |
| 4.0 | 19. Mai 1999 |
| 4.1 | 2. November 2000 |
| 4.2 | 1. November 2002 |
| 5.0 | 12. Juni 2003 |
| 5.1 | 25. Oktober 2004 |
| 5.2 | 20. Juni 2005 |
| 6.0 | 1. Mai 2007 |
| 7.0 | 18. November 2008 |
| 7.0.1 | 5. März 2009 |
| 8.0 | 15. November 2010 |
| 8.0.1 | 7. März 2011 |
| 8.0.4 | 24. Oktober 2011 |
| 9.0 | 28. November 2012 |
| 9.0.1 | 30. Januar 2013 |
| 10 | 9. Juli 2014 |
| 10.0.1 | 17. September 2014 |
| 10.0.2 | 15. Dezember 2014 |
| 10.1 | 31. März 2015 |
| 10.2 | 14. Juli 2015 |
| 10.3 | 15. Oktober 2015 |
| 10.3.1 | 16. Dezember 2015 |
| 10.4 | 2. März 2016 |
| 10.4.1 | 18. April 2016 |
| 11 | 9. August 2016 |
| 11.0.1 | 28. September 2016 |
| 11.1 | 16. März 2017 |
| 11.1.1 | 25. April 2017 |
| 11.2 | 14. September 2017 |
| 11.3 | 8. März 2018 |
| 12.0 | 16. April 2019 |
| 12.1 | 18. März 2020 |
| 12.2 | 16. Dezember 2020 |
| 12.3 | 20. Mai 2021 |
| 12.3.1 | Juli 2021 |
| 13.0 | 13. Dezember 2021 |
| 13.1 | 29. Juni 2022 |
| 13.2 | 14. Dezember 2022 |
| 13.2.1 | Februar 2023 |
| 13.3 | 12. Juni 2023 |
| 14.0 | 9. Januar 2024 |
| 14.1 | 31. Juli 2024 |
| 14.2 | 23. Januar 2025 |
Anbindung an andere Systeme und Sprachen
Die Kommunikation mit anderen Anwendungen und Diensten kann über ein Protokoll namens Wolfram Symbolic Transfer Protocol (WSTP) erfolgen.[20] WSTP ermöglicht die Kommunikation zwischen dem Wolfram Mathematica-Kernel und dem Frontend und bietet eine allgemeine Schnittstelle zwischen dem Kernel und anderen Anwendungen, die auch in anderen Sprachen programmiert sein können. Mathematica hat eine Schnittstelle für Haskell,[21] AppleScript,[22] Racket, Visual Basic,[23] Python[24] und Clojure.[25]
Probleme
2014 haben drei Mathematiker veröffentlicht, dass Mathematica bei der Berechnung von Determinanten bestimmter Matrizen mit recht großen Ganzzahlen (10.000 Stellen) falsche Ergebnisse liefert. Dieser Fehler sei 2013 gemeldet und auch nach über einem Jahr nicht behoben worden; die Darstellung von Wolfram Research widerspricht diesen Angaben jedoch in Teilen und geht von einem neuen Fehler aus.[26] Der Berechnungsfehler (CASE:303438) ist ab Version 11.1 behoben und nicht mehr vorhanden.
Siehe auch
- Wolfram Alpha
- Liste von Statistik-Software
- Wissenschaftliches Rechnen
- Sage (Software), Open Source Alternative
- Xcas
- Maple (Software)
Literatur
- Hans Benker: MATHEMATICA kompakt: Mathematische Problemlösungen für Ingenieure, Mathematiker und Naturwissenschaftler. Springer, Berlin / Heidelberg 2016, ISBN 978-3-662-49610-7.
- Stephen Wolfram: An Elementary Introduction to the Wolfram Language. Wolfram Media, Champaign IL 2023, ISBN 978-1-944183-07-3.
- Knut Lorenzen: Einführung in Mathematica: Berücksichtigt die kostenlose Version 10 für den Raspberry Pi. mitp Verlag, 2014, ISBN 978-3-8266-9666-4.
- Axel Kilian: Programmieren mit Wolfram Mathematica. Springer, Berlin / Heidelberg 2009, ISBN 978-3-642-04671-1.
- Michael Trott: The Mathematica GuideBook for Symbolics. Springer, 2006.
- Michael Trott: The Mathematica GuideBook for Programming. Springer, 2004.
- Michael Trott: The Mathematica GuideBook for Numerics. Springer, 2006.
- Michael Trott: The Mathematica GuideBook for Graphics. Springer, 2004.
- Stephen Wolfram: The Mathematica Book. 5. Auflage. Wolfram Media, 2004, ISBN 1-57955-022-3.
- Leonid Shifrin: Mathematica programming. (archive.org – kostenloses E-Book).
- David B. Wagner: Power Programming With Mathematica: The Kernel. McGraw-Hill Education, 1996, ISBN 0-07-912237-X (dropbox.com [PDF] kostenloses E-Book zu Mathematica).
Weblinks
- Wolfram Research, Inc.
- Offizielle Mathematica-Homepage des deutschen Partners
- Wolfram Alpha (auf Mathematica basierender Internetdienst von Wolfram Research).
- Der Mathematica Integrator
- List of numerical analysis software (englischsprachige Wikipedia)
- Mathematica auf dem Raspberry Pi. Kostenlose Mathematica-Version für nicht kommerzielle Nutzung.
Einzelnachweise
- ↑ Stephen Wolfram: Launching Version 14.2 of Wolfram Language & Mathematica: Big Data Meets Computation & AI. 23. Januar 2025.
- ↑ a b The Software Engineering of Mathematica. 2012 (abgerufen am 7. Januar 2019).
- ↑ Barak Katz: Introduction to Mathematica. (PDF; 1.6 MB) 2008, abgerufen am 27. März 2020 (englisch).
- ↑ Paritosh Mokhasi: Solving Differential Equations in Mathematica. In: WOLFRAM Computation meets knowledge. Abgerufen am 27. März 2020 (englisch, Webseite mit eingebettetem Video).
- ↑ Stephen Wolfram: Mathematica. A System for Doing Mathematics by Computer. Addison-Wesley Publishing Company, 1988, ISBN 0-201-19334-5, S. XVIII.
- ↑ Stephen Wolfram: Steve Jobs. A Few Memories. In: Stephen Wolfram. Writings. 6. Oktober 2011, abgerufen am 6. März 2020 (englisch).
- ↑ Stephen Wolfram: The mathematica book: Version 4. Fourth Edition Auflage. Wolfram Media; Cambridge University Press, Champaign IL, New York 1999, ISBN 1-57955-004-5 (xxvi, 1470 p.).
- ↑ The Story Continues: Announcing Version 14 of Wolfram Language and Mathematica. In: writings.stephenwolfram.com. Abgerufen am 16. Januar 2025.
- ↑ The Wolfram Function Repository: Launching an Open Platform for Extending the Wolfram Language. In: writings.stephenwolfram.com. Abgerufen am 16. Januar 2025.
- ↑ Cliff Hastings: First 10 Minutes with Mathematica 8. In: wolfram.com. Abgerufen am 5. Juni 2023.
- ↑ wolfram.com free form linguistic input
- ↑ Wolfram Mathematica. In: wolfram.com. Abgerufen am 16. Januar 2025.
- ↑ Heise, 15. November 2013: Mathematica-Chef Wolfram kündigt Programmiersprache an, Herstellerlink: Wolfram Programming Language
- ↑ wolfram.com Wolfram Language – Wissensbasiertes Programmieren
- ↑ Das übliche Malzeichen, das Sternchen (*) der Tabellenkalkulations-Programme und Programmiersprachen, bewirkt die elementweise Multiplikation.
- ↑ Die Wiedergabe hier entspricht nicht genau der Ausschrift von Mathematica, die der Screenshot zeigt. Es wurde der gemeinsame Nenner aller Matrixelemente herausgezogen.
- ↑ Emily Martin (Hrsg.): Mathematica 3.0: Standard Add-on Packages. Wolfram Media; Cambridge University Press, Champaign, Ill., Cambridge 1996, ISBN 0-9650532-2-9, S. 207 ff. (V, 516 p.).
- ↑ Polyhedron
- ↑ Mathematicas kurze Versionsgeschichte. Wolfram Mathematica, Februar 2023, abgerufen am 16. März 2023.
- ↑ wolfram.com
- ↑ hackage.haskell.org
- ↑ unisoftwareplus.com ( vom 17. Juli 2011 im Internet Archive)
- ↑ library.wolfram.com
- ↑ library.wolfram.com
- ↑ clojuratica.weebly.com
- ↑ heise.de
Auf dieser Seite verwendete Medien
Mathematica Logo
Autor/Urheber: HolyCookie, Lizenz: CC0
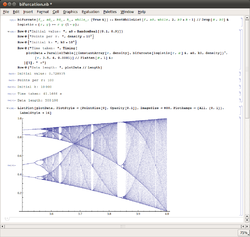
The image shows the Mathematica 8.0.0 (GNU/Linux) frontend, in which the bifurcation diagram of the logistic map is calculated.
Autor/Urheber: Roderich Kahn, Lizenz: CC BY-SA 4.0
Die fünf Platonischen Körper und ihre Stümpfe, die durch Abschneiden der Ecken entstehen, gezeichnet mit Standardfunktionen von Mathematica der Version 3.
Autor/Urheber: Quchen, Lizenz: CC0
Dini's surface with adjustable parameters, created with Mathematica 8.0.0/Linux.
Autor/Urheber: Sven, Lizenz: CC0
This is the TreeForm display of the software showing the expression
a+Sin[b*c].The PDF file was then converted to SVG with the Debian pdf2svg package.
Autor/Urheber: Roderich Kahn, Lizenz: CC BY-SA 4.0
Screenshot des Programms "Mathematica" zu Matrizenmanipulationen.