Müller-Lyer-Illusion

Die obere waagerechte Linie erscheint kürzer als die untere

Die Müller-Lyer-Illusion, auch Müller-Lyer-Täuschung, ist eine sehr bekannte geometrisch-optische Täuschung. Sie wurde 1889 von dem deutschen Psychiater und Soziologen Franz Müller-Lyer (1857–1916) entdeckt.^[1]

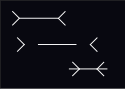
Das Phänomen: Eine horizontale Linie ist zwischen zwei Winkeln eingeschlossen, deren Spitzen mit den Linienenden zusammenfallen. Zeigen die Spitzen nach außen, dann erscheint die Linie deutlich kürzer, als wenn die Pfeilspitzen nach innen weisen.^[2][3] Für diese Täuschung existiert bis heute keine einhellige Erklärung.

• Ein Erklärungsansatz begründet das Phänomen mit dem Emmertschen Gesetz.

• Eine mangelhafte Koordinierung zwischen Gehirn und Augen stellt einen weiteren Erklärungsansatz für die Täuschung dar.

• Eine weitere Erklärung ist, dass die Konstrukte unbewusst als räumliche Objekte interpretiert werden, etwa als ausgebauchtes bzw. eingeschnürtes Gefäß, wobei die Mittellinien unbewusst den Längen der Ober- bzw. Unterkanten angenähert werden.

• 

  Die Linie wird durch die sie berührenden Pfeile gleichsam gedehnt (oben). Löst man diese Verbindung, wird die Linie scheinbar kürzer; und noch kürzer, wenn die Pfeilspitzen gegen die Mitte vorrücken.
  Die Täuschung kann auch als Kontexteffekt interpretiert werden, bei dem die wahrgenommene Länge der Linie in Wechselwirkung tritt mit dem subjektiv wahrgenommenen Abstand der Pfeile.^[4] Die Pfeile mit den Winkeln, die sie einschließen, bilden Quellen erhöhter geometrischer Information, die Aufmerksamkeit auf sich ziehen. Allerdings muss der Abstand dieser Informationsschwerpunkte nicht genau mit der Länge der Linie übereinstimmen, selbst wenn die Pfeilspitzen mit den Linienenden zusammenfallen. Diese Diskrepanz hängt wesentlich davon ab, ob sich die Pfeile von den Linienenden nach außen oder nach innen erstrecken, also zur Linienmitte zeigen oder von ihr weg, und auch von der Form der Pfeile. Da Linie und Pfeile auch eine Wahrnehmungseinheit bilden (wenn sie unmittelbar an einander anschließen oder überlappen), können sie einander in der Wahrnehmung beeinflussen. Dieser Einfluss wird deutlich, wenn man diese Einheit auflöst: Im Bild rechts erscheint die Linie mit den unmittelbar anschließenden, nach innen gerichteten Spitzen (oben) länger, als wenn Lücken gelassen werden und das Target weitgehend für sich allein betrachtet werden kann (Mitte). Noch kürzer erscheint sie, wenn die Pfeile gegen das Zentrum vorrücken und der Abstand der Informationsschwerpunkte deutlich kleiner wird als die Länge der Linie. Eine Möglichkeit, die eigene Fähigkeit der Linienlängeneinschätzung zu testen, findet sich bei Bach.^[5]

Der Evolutionswissenschaftler Joseph Henrich und seine Kollegen zeigten 2010 in einer kulturvergleichenden Studie, dass die Täuschung nur bei Menschen auftritt, in deren Lebensalltag überhaupt gerade Linien vorkommen. Für Menschen des San-Volkes besteht die Täuschung nicht und für viele andere Gruppen über die ganze Welt verteilt ist der Effekt nur minimal. Am stärksten nehmen die Täuschung Menschen des westlichen Kulturkreises wahr.^[6]

Einzelnachweise

1. ↑ Franz Müller-Lyer: Optische Urteilstäuschungen. Archiv für Physiologie Suppl. 263–270, 1889.
2. ↑ B. Lingelbach: Die Müller-Lyer-Täuschung. 2013.
3. ↑ Inga Menkhoff: Die Welt der optischen Illusionen, Parragon Books Ltd., S. 14 und 15.
4. ↑ W. A. Kreiner: Ingoing versus outgoing wings. The Müller-Lyer and the mirrored triangle illusion. 2012. doi:10.18725/OPARU-2594
5. ↑ M. Bach: Müller-Lyer-Täuschung.
6. ↑ Thomas Widlok, Niclas Burenhult: Sehen, riechen, orientieren. Spektrum der Wissenschaft, Juli 2014, S. 78.