Luftdichte

Die Luftdichte ρ (auch Dichte von Luft oder Dichte der Luft) gibt an, welche Masse Luft in einem bestimmten Volumen enthalten ist. Auf Meeresspiegelhöhe ist die Luft mit rund 1,2041 kg/m³ bei 20 °C durch die darüber lastende Luftmasse stärker verdichtet als in größerer Höhe.

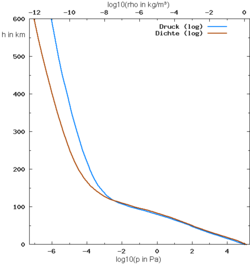
Luft ist um so dichter, je höher die Luftsäule über ihr ist. Darum hat Luft am Boden einen höheren Luftdruck als Luft über dem Boden. Eine Faustregel ist, dass der Luftdruck sich pro 5500 Meter Höhe halbiert. Anhand der Luftdichte lässt sich die Dichtehöhe als Näherung für die topografische Höhe bestimmen.

Auch die Temperatur beeinflusst die Luftdichte. Dabei spielen der atmosphärische Temperaturgradient und meteorologische Faktoren eine Rolle. In Bodennähe beeinflusst auch das Gelände die Temperatur; etwas höher können Inversionen Temperaturschwankungen verursachen. Wäre die Temperatur in allen Höhen gleich, so würden Luftdruck und Luftdichte gemeinsam mit zunehmender Höhe nach dem Gesetz für ideale Gase abnehmen (siehe barometrische Höhenformel).

Die Luftdichte verändert sich auch mit dem Anteil des in ihr enthaltenen Wasserdampf, weil Wassermoleküle eine geringere Masse als Stickstoffmoleküle (N₂) und Sauerstoffmoleküle (O₂) haben. Mit steigender Luftfeuchtigkeit sinkt also die Luftdichte.

In erster Näherung kann man die Luft als ein ideales Gas betrachten, dessen Dichte ρ (rho) man nach der folgenden Gleichung für ideale Gase berechnen kann:

${\displaystyle \rho ={\frac {p\cdot M}{R\cdot T}}}$^[1]

mit

• dem Luftdruck p (Standard-Atmosphärendruck: ${\displaystyle p_{0}=1013,25\,{\text{hPa}}}$^[2] ),
• der molaren Masse M (mittlere molare Masse der trockenen Luft = ${\displaystyle {\begin{aligned}\mathrm {28{,}96\ g\cdot mol^{-1}} \end{aligned}}}$),
• der Universellen Gaskonstante ${\displaystyle R\approx 8,314462618\,{\frac {\text{J}}{{\text{mol}}\cdot {\text{K}}}}}$^[3],
• der Temperatur T.

Durch Einsetzen der spezifischen Gaskonstante ${\displaystyle R_{\mathrm {S} }={\tfrac {R}{M}}=287{,}1\ \mathrm {\tfrac {J}{kg\cdot K}} }$ für trockene Luft^[4] erhält man:

${\displaystyle \rho ={\frac {p}{R_{\mathrm {S} }\cdot T}}}$.

Eine genauere Dichtebestimmung der Luft erfordert eine Berücksichtigung der Luftfeuchte, da diese die Gaskonstante der Luft verändert:

${\displaystyle R_{\mathrm {f} }={\frac {R_{\mathrm {S} }}{1-\varphi \cdot {\frac {p_{\mathrm {d} }}{p}}\cdot {\Big (}1-{\frac {R_{\mathrm {S} }}{R_{\mathrm {d} }}}{\Big )}}}}$

mit

• der Gaskonstante ${\displaystyle R_{\mathrm {S} }=287{,}058\,\mathrm {\tfrac {J}{kg\cdot K}} }$ der trockenen Luft
• der Gaskonstante ${\displaystyle R_{\mathrm {d} }=461{,}523\,\mathrm {\tfrac {J}{kg\cdot K}} }$ von Wasserdampf
• der relativen Luftfeuchtigkeit ${\displaystyle \varphi }$ (z. B.:  0,76 = 76 %)
• dem Sättigungsdampfdruck ${\displaystyle p_{\mathrm {d} }}$ von Wasser in Luft^[5]
• dem Umgebungsdruck ${\displaystyle p}$

Nachdem die Gaskonstante angepasst wurde, kann die Gleichung

${\displaystyle \rho ={\frac {p}{R_{\mathrm {f} }\cdot T}}}$

verwendet werden.

Der reziproke Wert der Dichte, das spezifische Volumen, hat in der Meteorologie das Formelzeichen α und in der Thermodynamik das Formelzeichen v_Luft:

${\displaystyle \alpha =v_{\text{Luft}}={\frac {1}{\rho }}}$.

1. ↑ 11.4: The Ideal Gas Law. 12. Februar 2015, abgerufen am 2. April 2025 (englisch). 
2. ↑ Wetter und Klima - Deutscher Wetterdienst - Glossar - Standardatmosphäre. Abgerufen am 2. April 2025. 
3. ↑ Fundamental Physical Constants from NIST. Abgerufen am 2. April 2025 (englisch). 
4. ↑ Hans-Joachim Kretzschmar, Ingo Kraft: Kleine Formelsammlung Technische Thermodynamik (= Hanser eLibrary). 6., überarbeitete Auflage. Hanser, München 2022, ISBN 978-3-446-47321-8, S. 182. 
5. ↑
   

   Wikibooks: Datentabelle mit genaueren Formeln – Lern- und Lehrmaterialien

   tabelliert ist. Es gibt auch empirische Formeln unterschiedlicher Genauigkeit wie die Magnus-Formel oder Antoine-Gleichung.