Lokal zusammenziehbarer Raum

Ein lokal kontrahierbarer oder lokal zusammenziehbarer Raum wird im mathematischen Teilgebiet der Topologie betrachtet.

Definition

Ein topologischer Raum ${\displaystyle X}$ heißt lokal zusammenziehbar, wenn es zu jeder Umgebung ${\displaystyle U\subset X}$ jedes Punktes ${\displaystyle x\in X}$ eine zusammenziehbare Umgebung ${\displaystyle V\subset X}$ mit

${\displaystyle x\in V\subset U}$

gibt.^[1]

Beispiele

Topologischer Kamm

Mannigfaltigkeiten und CW-Komplexe sind lokal zusammenziehbar.

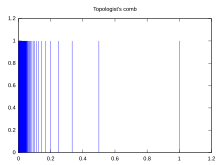
Zusammenziehbare Räume müssen nicht immer lokal zusammenziehbar sein. Ein Beispiel hierfür ist der topologische Kamm, dieser ist definiert als

${\displaystyle (\{0\}\times [0,1])\cup (\{1/n|n\in \mathbb {N} \}\times [0,1])\cup ([0,1]\times \{0\})\subset \mathbb {R} ^{2}}$

mit der von der euklidischen Metrik des ${\displaystyle \mathbb {R} ^{2}}$ induzierten Topologie.

Einzelnachweise

1. ↑ John Gilbert Hocking, Gail S. Young: Topology. Dover Publications, New York 1988, ISBN 0-486-65676-4, S. 191.