Liste der Quantengatter

Die Notation für Quantengatter wurde von den Begründern der Quanteninformatik, daruntern Adriano Barenco, Charles Bennett, Richard Cleve, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin und Harald Weinfurter entwickelt.^[1]

Dies ist eine Auflistung verschiedener Quantengatter und deren Funktion.

Quantengatter mit einem Eingang

Quantengatter, die sich auf einzelne Quantenbits beziehen
Symbol und Funktion¹	Bezeichnung	Funktion	Beschreibung
	Identität	${\begin{pmatrix}1&0\\0&1\end{pmatrix}}$	Identität des hyperkomplexen Eingangs und daher keine Veränderung am Quantenzustand
	Pauli-X-Gatter Nicht-Gatter	${\begin{pmatrix}0&1\\1&0\end{pmatrix}}=\left\|1\right\rangle \left\langle 0\right\|+\left\|0\right\rangle \left\langle 1\right\|$	Spiegelung des hyperkomplexen Eingangs an der X-Achse Beispiel: $X\left\|0\right\rangle =\left\|1\right\rangle$
	Pauli-Y-Gatter	${\begin{pmatrix}0&-i\\i&0\end{pmatrix}}=i\left\|1\right\rangle \left\langle 0\right\|-i\left\|0\right\rangle \left\langle 1\right\|$	Spiegelung des hyperkomplexen Eingangs an der Y-Achse Beispiel: $Y\left\|0\right\rangle =i\left\|1\right\rangle$
	Pauli-Z-Gatter	${\begin{pmatrix}1&0\\0&-1\end{pmatrix}}=\left\|0\right\rangle \left\langle 0\right\|-\left\|1\right\rangle \left\langle 1\right\|$	Spiegelung des hyperkomplexen Eingangs an der Z-Achse
	Hadamard-Gatter	${\frac {1}{\sqrt {2}}}\cdot {\begin{pmatrix}1&1\\1&-1\end{pmatrix}}$	Spiegelung des hyperkomplexen Eingangs an der X+Z-Achse
	X-Rotationsgatter	${\frac {1}{\sqrt {2}}}\cdot {\begin{pmatrix}1&-i\\-i&1\end{pmatrix}}$	Dreht den komplexen Eingang 90° (π/2) um die X-Achse Auch als ${\sqrt {\mathrm {NOT} }}$ -Gatter bezeichnet.
	Y-Rotationsgatter	${\frac {1}{\sqrt {2}}}\cdot {\begin{pmatrix}1&-1\\1&1\end{pmatrix}}$	Dreht den hyperkomplexen Eingang 90° (π/2) um die Y-Achse
	(−X)-Rotationsgatter	${\frac {1}{\sqrt {2}}}\cdot {\begin{pmatrix}1&i\\i&1\end{pmatrix}}$	Dreht den komplexen Eingang −90° (−π/2) um die X-Achse
	(−Y)-Rotationsgatter	${\frac {1}{\sqrt {2}}}\cdot {\begin{pmatrix}1&1\\-1&1\end{pmatrix}}$	Dreht den hyperkomplexen Eingang −90° (−π/2) um die Y-Achse
	S-Gatter, Phasengatter	${\begin{pmatrix}1&0\\0&i\end{pmatrix}}=\left\|0\right\rangle \left\langle 0\right\|+i\left\|1\right\rangle \left\langle 1\right\|$	Dreht die Phase 90° (π/2) um die Z-Achse Auch als ${\sqrt {\mathrm {Z} }}$ -Gatter bezeichnet.
	T-Gatter, π/8-Gatter Phasen(schieber)gatter	${\begin{pmatrix}1&0\\0&e^{\frac {i\pi }{4}}\end{pmatrix}}=\left\|0\right\rangle \left\langle 0\right\|+e^{\frac {i\pi }{4}}\left\|1\right\rangle \left\langle 1\right\|$	Dreht die Phase 45° (π/4) um die Z-Achse Auch als ${\sqrt {\mathrm {S} }}$ -Gatter bezeichnet.
	Allgemeines Phasen(schieber)gatter^2,3.	${\begin{pmatrix}1&0\\0&e^{\frac {i\pi }{2^{k}}}\end{pmatrix}}=\left\|0\right\rangle \left\langle 0\right\|+e^{\frac {i\pi }{2^{k}}}\left\|1\right\rangle \left\langle 1\right\|$	k wird willkürlich festgelegt Dreht die Phase π/2^k um die Z-Achse.
	Willkürliches unitäres Gatter³	${\begin{pmatrix}a&b\\-b^{}&a^{}\end{pmatrix}}$ mit $\left\|a\right\|^{2}+\left\|b\right\|^{2}=1$	Alle Eigenschaften werden willkürlich festgelegt
¹Am Beispiel drei verschiedener Eingangssignale mit verschiedenen Spins und deren Lage nach dem Durchqueren des Gatters. Die Z-Achse (am Eingang Blau) gibt den reellen Wert, die X- (am Eingang Rot) und Y-Achse (am Eingang Grün) die Phasenlage wieder. Der Eingang ist mit A, der Ausgang mit A' gekennzeichnet. Siehe auch: Bloch-Kugel ²Ausgang dargestellt für die Werte k = 0, k = 1 und k = 2 ³Ausgang abhängig von den verwendeten Parametern

Quantengatter mit zwei Eingängen

Quantengatter, die sich auf zwei Quantenbits beziehen
Bezeichnung	Funktion	Beschreibung
Kontrolliertes-Nicht-Gatter (CNOT, XOR-Verknüpfung)	$\left\|00\right\rangle \to \left\|00\right\rangle$ $\left\|01\right\rangle \to \left\|01\right\rangle$ $\left\|10\right\rangle \to \left\|11\right\rangle$ $\left\|11\right\rangle \to \left\|10\right\rangle$ Matrixdarstellung ${\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\\\end{pmatrix}}$	Der reelle Wert des zweiten Qubits (Zielqubit B) wird in Abhängigkeit vom reellen Wert des ersten Qubits (Kontrollqubit A) entweder beibehalten (A=0) oder negiert (A=1). $B'\leftarrow A\oplus B=\left(\neg A\land B\right)\vee \left(\neg B\land A\right)$ Der Wert des ersten Qubits wird beibehalten. $A'\leftarrow A\,$
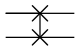Austauschknoten („Swap“)	$\left\|00\right\rangle \to \left\|00\right\rangle$ $\left\|01\right\rangle \to \left\|10\right\rangle$ $\left\|10\right\rangle \to \left\|01\right\rangle$ $\left\|11\right\rangle \to \left\|11\right\rangle$ Matrixdarstellung: ${\begin{pmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\end{pmatrix}}$	Die beiden Eingangs-Qubits werden vertauscht
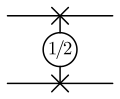Wurzel Swap	${\begin{pmatrix}1&0&0&0\\0&{\frac {1}{2}}(1+i)&{\frac {1}{2}}(1-i)&0\\0&{\frac {1}{2}}(1-i)&{\frac {1}{2}}(1+i)&0\\0&0&0&1\end{pmatrix}}$	Universelles Gatter, das die Eingangs-Qubits halb vertauscht
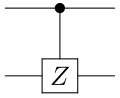Kontrollierter Z-flip (CZ)	${\left\|11\right\rangle }\to -{\left\|11\right\rangle }$	Auch als kontrolliertes Z-Gatter, kontrollierter Phasenflip (CPF) oder controlled-SIGN (CSIGN) bezeichnet
Kontrollierte Phase (C-Phase)	${\left\|11\right\rangle }\to e^{\frac {2i\pi }{2^{k}}}\cdot {\left\|11\right\rangle }$	$k$ kann beliebig gewählt werden.
Kontrolliertes $U$	$\left\|0\phi \right\rangle \to \left\|0\phi \right\rangle$ $\left\|1\phi \right\rangle \to \left\|1\right\rangle {\begin{pmatrix}x_{00}&x_{10}\\x_{01}&x_{11}\end{pmatrix}}\cdot \left\|\phi \right\rangle$ Matrixdarstellung: ${\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&x_{00}&x_{10}\\0&0&x_{01}&x_{11}\\\end{pmatrix}}$ Dirac-Darstellung: $\left\|00\right\rangle \left\langle 00\right\|$ + $\left\|01\right\rangle \left\langle 01\right\|$ + $x_{00}\left\|10\right\rangle \left\langle 10\right\|$ + $x_{01}\left\|10\right\rangle \left\langle 11\right\|$ + $x_{10}\left\|11\right\rangle \left\langle 10\right\|$ + $x_{11}\left\|11\right\rangle \left\langle 11\right\|$	Das zweite Qubit wird gemäß der unitären Abbildung $U$ transformiert falls das erste Qubit den Wert „1“ hat und bleibt ansonsten unverändert. (C-NOT und C-Phase sind Spezialfälle von C-U)
Beliebige unitäre Transformation	$\left\|\psi \right\rangle \to U\cdot \left\|\psi \right\rangle$	Die unabhängigen Variablen der komplexen unitären 4x4-Matrix (16 reelle Parameter) können beliebig gewählt werden. Auf diese Weise kann man alle Wechselwirkungen zwischen den beiden Qubits beschreiben.

Quantengatter mit drei Eingängen

Quantengatter, die sich auf drei Quantenbits beziehen.
Bezeichnung	Funktion	Beschreibung
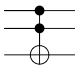Toffoli-Gatter	$\left\|111\right\rangle \leftrightarrow \left\|110\right\rangle$ $\left\|0yx\right\rangle \leftrightarrow \left\|0yx\right\rangle$ $\left\|10x\right\rangle \leftrightarrow \left\|10x\right\rangle$ ${\begin{pmatrix}1&0\\1&1\end{pmatrix}}\cdot {\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}x\\x\oplus y\end{pmatrix}}$ Matrixdarstellung: ${\begin{pmatrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&1\\0&0&0&0&0&0&1&0\end{pmatrix}}$	Die ersten beiden Qubits (A und B) bleiben unverändert. $A'\leftarrow A\,$ $B'\leftarrow B\,$ Der reelle Wert des dritten Qubits (C) wird negiert, wenn der reelle Wert der ersten beiden Qubits positiv (d. h. logisch 1) ist. $C'\leftarrow C\oplus \left(A\land B\right)\,$ Das Toffoli-Gatter kann logische AND-, XOR-, NOT- und FANOUT-Operationen durchführen, wodurch es universell für klassische Berechnungen eingesetzt werden kann.
Fredkin-Gatter	$\left\|001\right\rangle \leftrightarrow \left\|010\right\rangle$ $\left\|010\right\rangle \leftrightarrow \left\|001\right\rangle$ $\left\|101\right\rangle \leftrightarrow \left\|101\right\rangle$ $\left\|110\right\rangle \leftrightarrow \left\|110\right\rangle$ …	Das Fredkin-Gatter vertauscht das zweite und dritte Qubit, wenn der reelle Wert des ersten Qubits negativ (d. h. logisch 0) ist.
Deutsch-Gatter	$\|11x\rangle \rightarrow \|11(1-x)\rangle \cdot \sin(\theta )+i\cdot \|11x\rangle \cdot \cos(\theta )$	Das Deutsch-Gatter ist ein universelles Drei-Qubit-Gatter, mit dem beliebige Wechselwirkungen der ersten beiden Qubits auf das dritte Qubit erfolgen können. Die ersten beiden Qubits werden nicht verändert.¹

Siehe auch

Einzelnachweise

↑ Bennett, Cleve, DiVincenzo, Margolus, Sleator, Smolin, Weinfurter: Elementary gates for quantum computation. In: Physical Review A. Band 52, Nr. 5. American Physical Society (APS), 1. November 1995, ISSN 1050-2947, S. 3457–3467, doi:10.1103/physreva.52.3457, arxiv:quant-ph/9503016.

[Barenco-1] Bennett, Cleve, DiVincenzo, Margolus, Sleator, Smolin, Weinfurter: Elementary gates for quantum computation. In: Physical Review A. Band 52, Nr. 5. American Physical Society (APS), 1. November 1995, ISSN 1050-2947, S. 3457–3467, doi:10.1103/physreva.52.3457, arxiv:quant-ph/9503016.

[1]

Navigation

Navigation

Themenportale

Werbung