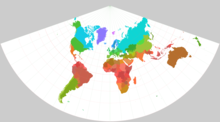
Lamberts winkeltreue Kegelprojektion

Weltkarte in Lambertscher Kegelprojektion

Lamberts winkeltreue Kegelprojektion mit Standardparallelen bei 15°N und 45°N, Darstellung der Verzerrung durch die Tissotsche Indikatrix

Lamberts winkeltreue Kegelprojektion (auch Lambert-Gaußsche winkeltreue Kegelprojektion) ist ein 1772 von Johann Heinrich Lambert entwickelter, vielfach verwendeter Kartennetzentwurf. Sie ist eine winkeltreue (d. h. konforme) Kegelprojektion in normaler Lage.

Die Abbildung kann sowohl mit Berührkegel (d. h. mit einem längentreuen Parallelkreis) als auch mit einem Schnittkegel (d. h. mit zwei längentreuen Parallelkreisen) ausgeführt werden. Bei einer polykonischen Projektion werden mehrere Schnittkegel an den längentreuen Schnittkreisen zusammengefügt. Die Streifen werden dabei schmal gehalten, um die Verzerrungen zu minimieren.

Einige Karten in der Luftfahrt sind Lambertkarten, so zum Beispiel die ICAO-VFR-Karte für Sichtflüge oder IFR-Karten für Instrumentenflüge in den mittleren Breiten. In der Seefahrt werden demgegenüber überwiegend Karten in Mercatorprojektion eingesetzt. Auch die Internationale Weltkarte setzt die Lambertsche Projektion ein.

Transformation

Lamberts winkeltreue Kegelprojektion lässt sich unter Voraussetzung der Kugelgestalt durch folgende Formeln beschreiben, wobei ${\displaystyle R}$ den Erdradius, ${\displaystyle \lambda }$ die Länge, ${\displaystyle \lambda _{0}}$ die Referenzlänge, ${\displaystyle \varphi }$ die Breite, ${\displaystyle \varphi _{0}}$ die Referenzbreite und ${\displaystyle \varphi _{1}}$ bzw. ${\displaystyle \varphi _{2}}$ die Breite einer Standardparallele bezeichnet:^[1]

${\displaystyle {\begin{aligned}x&=\rho \sin \left[n\left(\lambda -\lambda _{0}\right)\right]\\y&=\rho _{0}-\rho \cos \left[n\left(\lambda -\lambda _{0}\right)\right]\end{aligned}}}$

Dabei werden folgende Bezeichnungen verwendet:

${\displaystyle {\begin{aligned}n&={\frac {\ln \left(\cos \varphi _{1}\sec \varphi _{2}\right)}{\ln \left[\tan \left({\frac {1}{4}}\pi +{\frac {1}{2}}\varphi _{2}\right)\cot \left({\frac {1}{4}}\pi +{\frac {1}{2}}\varphi _{1}\right)\right]}}\\F&={\frac {\cos \varphi _{1}\tan ^{n}\left({\frac {1}{4}}\pi +{\frac {1}{2}}\varphi _{1}\right)}{n}}\\\rho &=RF\cot ^{n}\left({\tfrac {1}{4}}\pi +{\tfrac {1}{2}}\varphi \right)\\\rho _{0}&=RF\cot ^{n}\left({\tfrac {1}{4}}\pi +{\tfrac {1}{2}}\varphi _{0}\right)\end{aligned}}}$

Wenn die Standardparallelen zusammenfallen (${\displaystyle \varphi _{1}=\varphi _{2}}$), liefert die obige Formel für ${\displaystyle n}$ kein Ergebnis; stattdessen ist dann ${\displaystyle n=\sin(\varphi _{1})}$ zu verwenden.

Einzelnachweise

1. ↑ John P. Snyder, Map Projections - A Working Manual, U.S. Geological Survey Professional Paper 1395, 1987, S. 106f.