Korrelogramm

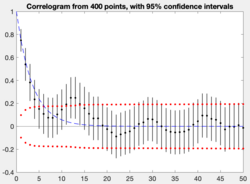
Ein Korrelogramm ist die graphische Darstellung der Autokorrelation einer Zeitreihe. Dazu werden die geschätzten Korrelationskoeffizienten ${\displaystyle {\hat {\rho }}_{l}}$ gegen die Dauer der Zeitverschiebung ${\displaystyle l}$ abgetragen.

Mit dem Korrelogramm kann untersucht werden, ob eine signifikante Autokorrelation bei einer Zeitverschiebung vorliegt. Die Nullhypothese ist, dass keine Autokorrelation vorliegt.

Dazu wird Konfidenzintervall der geschätzten Korrelationskoeffizienten betrachtet:

${\displaystyle B=\pm t_{1-\alpha /2}\,SE({\hat {\rho }}_{l}),}$

mit

• dem entsprechenden ${\displaystyle \alpha }$ Perzentil der t-Verteilung für die Irrtumswahrscheinlichkeit für den Fehler 1. Ordnung (Signifikanzniveau)
• dem Standardfehler SE

Liegt ${\displaystyle {\hat {\rho }}_{l}}$ in dem Intervall ${\displaystyle B}$, so wird die Nullhypothese mit einer Irrtumswahrscheinlichkeit von ${\displaystyle \alpha }$ abgelehnt.

Der Standardfehler SE wird in diesem Zusammenhang meist anhand Bartletts Formel für MA(l)-Prozesse berechnet (moving average, siehe dazu ARMA-Modell):

für ${\displaystyle l=1}$: ${\displaystyle SE({\hat {\rho }}_{1})={\frac {1}{T}}}$

für ${\displaystyle l>1}$: ${\displaystyle SE({\hat {\rho }}_{l})={\sqrt {\frac {1+2\sum _{i=1}^{l-1}{\hat {\rho }}_{i}^{2}}{T}}}}$

• der geschätzten Autokorrelation ${\displaystyle {\hat {\rho }}_{l}}$ zwischen Beobachtungen, die ${\displaystyle l}$ Perioden auseinanderliegen.

Im Bild wird daher die Nullhypothese (dass keine Autokorrelation zwischen benachbarten Perioden besteht) bei den ersten vorliegenden Verzögerung verworfen, da dort die Null nicht innerhalb des Konfidenzintervalls liegt. Für diese ersten Verzögerungen gilt, dass direkt aufeinanderfolgender Zeitpunkte signifikant korreliert sind. Für die übrigen Verzögerungen kann die Nullhypothese fehlender Autokorrelation allerdings nicht abgelehnt werden.

Siehe auch

• Portmanteau-Test

Weblinks

• Bootstrapping time series data ⋆ Quantdare. In: Quantdare. 28. Juni 2018, abgerufen am 2. Oktober 2021 (britisches Englisch). 

Literatur

• John E. Hanke, Arthur G. Reitsch, Dean W. Wichern: Business forecasting. 7. Aufl. Prentice Hall, Upper Saddle River, NJ 2001, ISBN 0-13-087810-3.